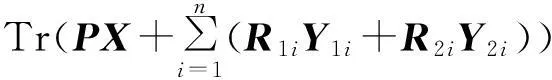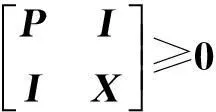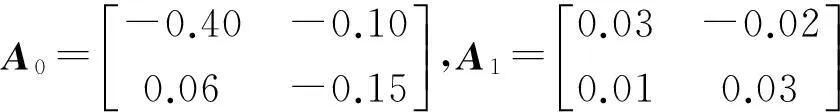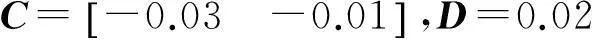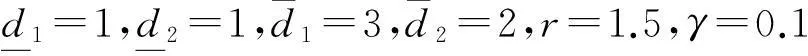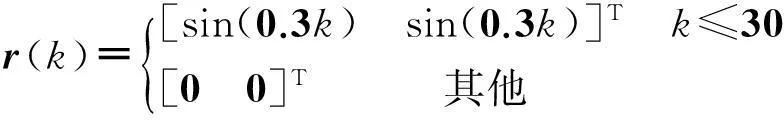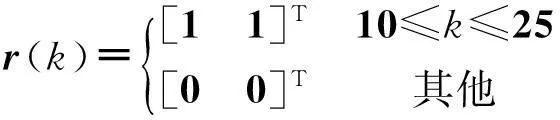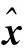基于观测器的多时变时滞系统H∞输出跟踪控制
2016-01-22范一心何熊熊
张 霓,范一心,何熊熊
(浙江工业大学 信息工程学院,浙江 杭州 310023)
基于观测器的多时变时滞系统H∞输出跟踪控制
张霓,范一心,何熊熊
(浙江工业大学 信息工程学院,浙江 杭州 310023)
摘要:针对一类具有多重时变时滞的离散时间系统,研究该系统基于状态观测器的H∞输出跟踪控制问题,其中参考信号由给定的参考模型生成.利用Lyapunov稳定性理论,线性矩阵不等式分析技巧以及自由权矩阵等方法,给出了跟踪误差系统指数稳定并满足H∞性能的充分条件,所得结果依赖系统时滞,具有较小的保守性.通过锥补线性化方法,将涉及状态观测器和反馈控制器设计的非线性问题,转化为由线性矩阵不等式组约束的非线性规划问题,数值仿真验证了结论的有效性.
关键词:离散系统;多时变时滞;输出跟踪控制;状态观测器;指数稳定
时滞现象普遍存在于各种控制系统中,往往导致系统不稳定或性能恶化,因此有关时滞系统稳定性和性能分析得到了广泛的关注[1-7].目前对时滞系统的研究多采用自由权矩阵等方法以获取保守性更低的结论,文献[3]研究了一类具有非线性扰动的时滞中立系统的跟踪控制问题,基于自由权矩阵方法,给出了跟踪误差系统稳定且满足H∞性能的时滞依赖充分性条件.输出跟踪控制是广泛应用于工程实践中的一类基本控制问题,例如机器人控制[8]和飞行器控制[9]等,其主要目标是抑制外部扰动对系统性能的影响和使系统输出无静差地跟踪外部参考输入[3-4,10-12].文献[4]基于干扰观测器,研究了一类具有时变时滞的离散时间切换系统的H∞输出跟踪控制问题,通过构造合适的干扰观测器,得到干扰信号的估计值,并与反馈控制器一起组成复合控制器,抵消输入信道的干扰信号的同时保证系统稳定并得到理想的H∞性能指标.文献[10]主要研究了一类不确定离散时滞系统的H2/H∞输出跟踪控制问题,给出了闭环系统在特定切换信号下鲁棒渐近稳定,并且满足混合H2/H∞性能指标的充分条件,设计了状态反馈跟踪控制器,但是文献[4,10]仅考虑了单时滞的情形.
由于系统状态在工程实践中难以直接测量,通常用受控系统的重构状态代替真实状态组成状态反馈,因此基于状态观测器的控制问题显得尤其重要[13-14].文献[13]研究了基于观测器的时滞切换系统的输出跟踪控制问题,通过引入符号系统简化分析过程,利用常数变易公式引入自由权矩阵等方法,设计了基于量测输出的概率切换控制律和基于平均驻留时间的控制器.文献[14]研究了基于观测器的离散时间网络预测控制系统的跟踪控制问题,其中前向通路和反馈回路的网络诱导时延服从取值有限的马尔科夫链随机过程,并且概率转移矩阵元素具有不确定性.综观现有的基于观测器的时滞系统跟踪控制问题,鲜有考虑被控对象含有多重时变状态时滞的情况,以此为出发点,研究了具有多重时变时滞的离散时间系统基于状态观测器的H∞输出跟踪控制问题,其中参考信号由给定的参考模型生成,利用Lyapunov稳定性理论,LMI分析技巧以及自由权矩阵等方法,给出了跟踪误差系统满足指数稳定和H∞性能的时滞依赖充分条件,通过锥补线性化方法,将非凸可行性问题转化为由LMI组约束的非线性规划问题,通过Matlab LMI工具箱求得状态观测器和反馈控制器,数值仿真验证了结论的有效性.
1问题描述
考虑如下具有多重时变时滞的离散系统(S):
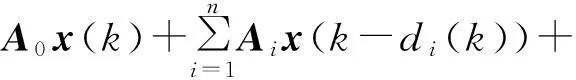
B1u(k)+B2w(k)
(1)
y(k)=Cx(k)+Du(k)
(2)
(3)
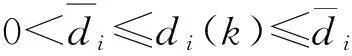
考虑如下形式的状态观测器:
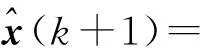
(4)
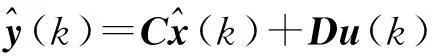
(5)

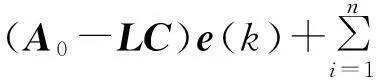
di(k))+B2w(k)
(6)
参考信号yr(k)由以下系统(Sr)生成:
xr(k)=Arxr(k)+Brr(k)
(7)
yr(k)=Crxr(k)
(8)
式中:xr(k)为参考状态;r(k)∈L2[0,∞)为参考输入;Ar为适维Hurwitz矩阵;Br,Cr为适维常矩阵.

(9)
式中K1和K2为反馈控制器增益.
x(k+1)=(A0+B1(K1+K2))x(k)+
B1K2xr(k)+B2w(k)
(10)
y(k)=(A+D(Κ1+K2)x(k)-D(K1+
K2)e(k)-DK2xr(k)
(11)
记系统(S)输出跟踪误差为er(k)=y(k)-yr(k),则
er(k)=(C+D(K1+K2))x(k)-D(K1+K2)e(k)-
(DK2+Cr)xr(k)
(12)
整理式(6,7,10)可得跟踪误差系统(Sacl):
(13)
(14)
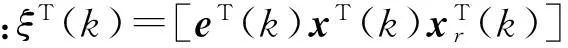
因此,控制器式(9)可以改写成
u(k)=(K1Hk1+K2Hk2)ξ(k)
(15)
定义1[13]给定常数r>1,γ>0,如果以下两个条件成立:
1) 当v(k)=0时,对任意初始状态(k0,φ)∈Z+×Cm,不等式
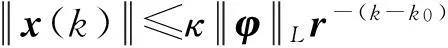
(16)

2) 在零初始状态ξ(k0)=0下,对于非零扰动v(k)∈L2[0,∞),不等式
(17)
成立,其中γ>0为H∞性能界,则称闭环系统(Sacl)指数稳定且满足H∞性能指标.
2基于状态观测器的H∞输出跟踪性能分析
定理1给定参数r>1,γ>0,如果存在对称正定矩阵P,Q1i,Q2i,Q3i,R1i,R2i,存在适维矩阵M1i,M2i,N1i,N2i,T1i,T2i(i=1,…,n)以及存在L,K1,K2,使得以下不等式成立:
(18)
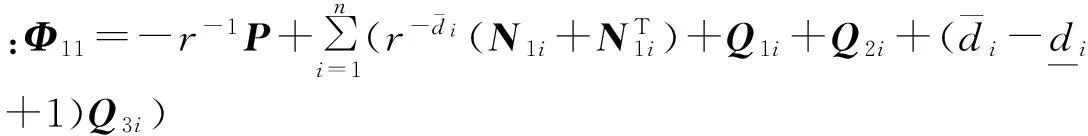
则闭环系统(Sacl)在基于观测器的状态反馈控制器式(15)作用下指数稳定且满足H∞性能指标.
证明选取Lyapunov函数为
(19)
式中:V1(ξ(k))=ξT(k)Pξ(k); V2(ξ(k))=
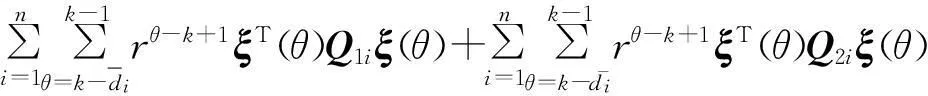
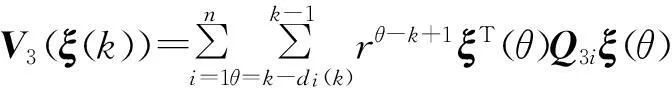
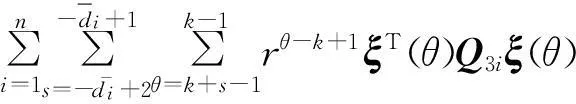
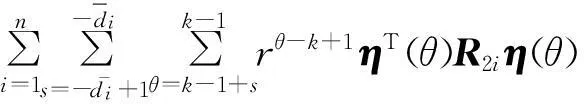
沿系统轨迹依次对Vi(ξ(k))作前向差分,并结合如下的Newton-Leibniz公式:
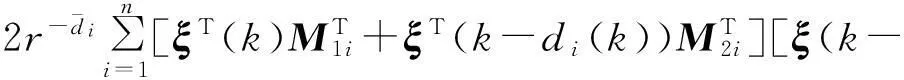
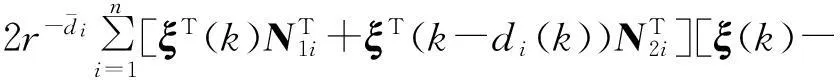
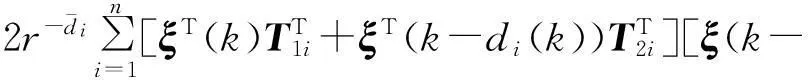
经过简单计算,可得
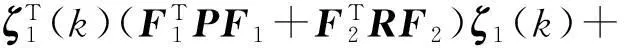
(r-1-1)V(ξ(k))
(20)
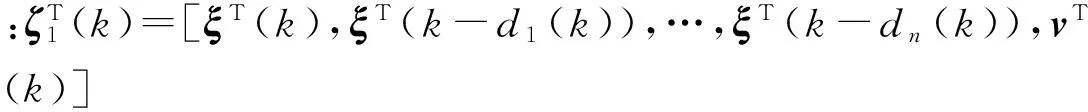
由式(20)进一步可知:

所以有
(21)
由式(18)以及舒尔补定理[15]易知不等式(21)等价于
(22)
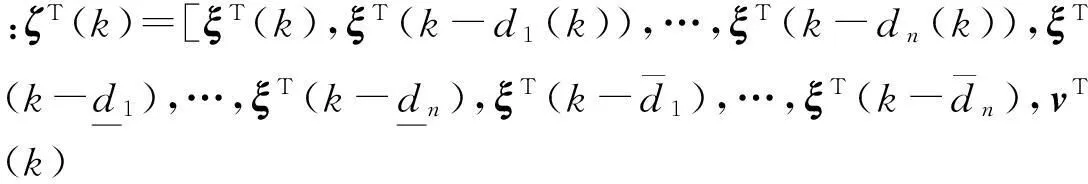
当v(k)=0时,由式(22)可得
r-(k-k0)V(ξ(k0))
(23)
记β1=λmin(P)
由式(19)可知:
进一步结合式(23)有
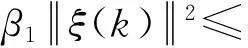
因此可得
在零初始状态ξ(k0)=0下,对于非零扰动v(k)∈L2[0,∞),由(22)可知:
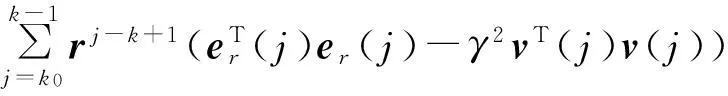
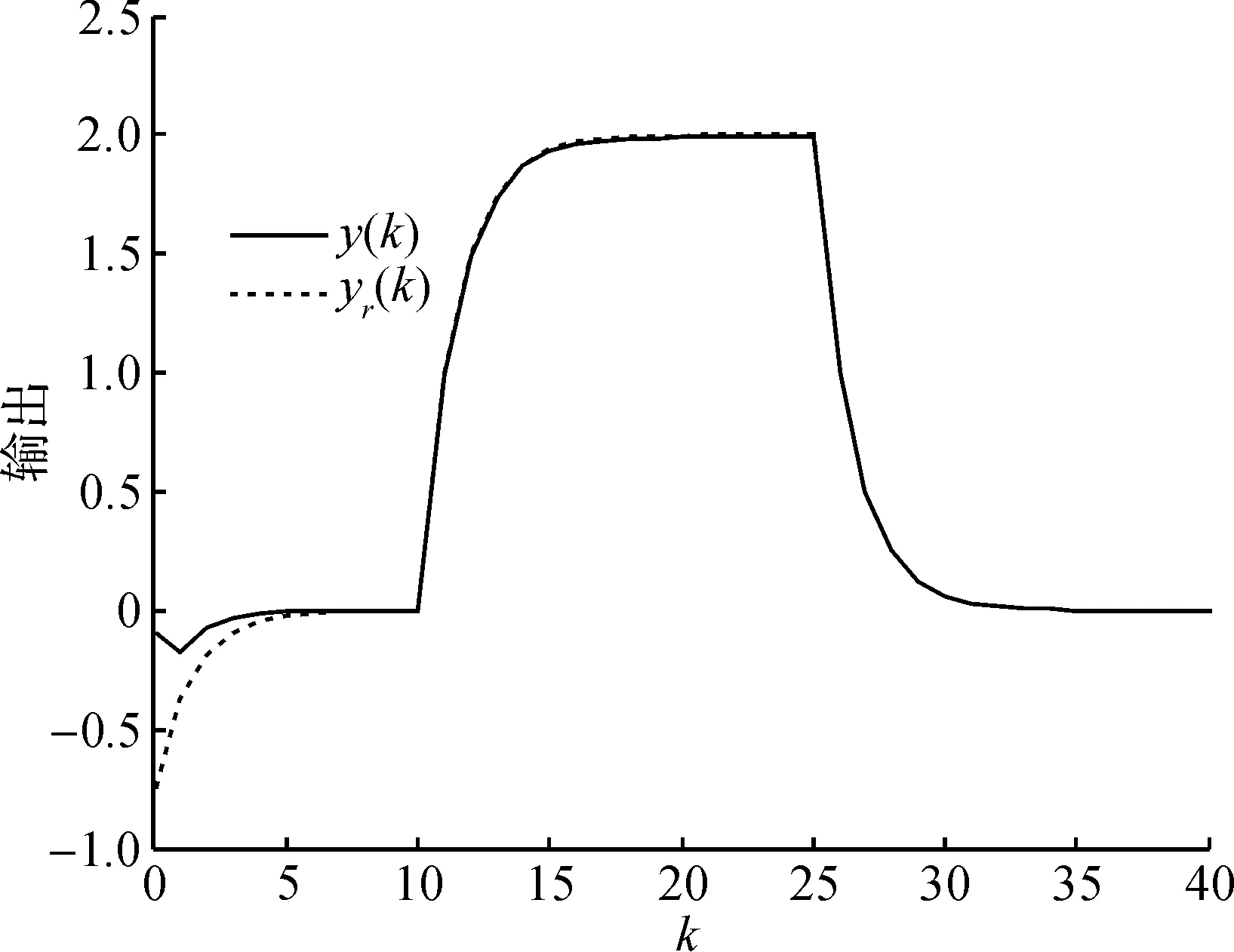
r-(k-k0)V(ξ(k0))-V(ξ(k)) 又因为rj-k+1>0,所以当k→∞时: 综上所述,由定义1可知:系统(Sacl)指数稳定且满足H∞性能指标,定理1得证. 3状态观测器和H∞输出跟踪控制器的求解 (24) (25) 下面给出求解该最小化问题的算法: 1) 求得满足式(24,25)的一组可行解: (P,X,Q1i,Q2i,Q3i,R1i,R2i,Y1i,Y2i,M1i,M2i, N1i,N2i,T1i,T2i,L,K1,K2)0 验证所得最优解是否满足式(18),若满足,则得解;若不满足,令k=0执行步骤2). 2) 求解以下具有LMI组约束的最小化问题: 使得式(24,25)成立. 3) 验证所得最优解是否满足式(18),若满足,则得解;若不满足;检查k是否达到规定的迭代次数,如果达到,则无解;否则,令k=k+1,令求出的最优解为 (P,X,Q1i,Q2i,Q3i,R1i,R2i,Y1i,Y2i,M1i,M2i,N1i, N2i,T1i,T2i,L,K1,K2)k+1 继续执行步骤2). 4仿真实例 考虑如式(1,2,3)具有多时变时滞的离散系统(S),系统参数如下: 考虑如式(7,8)参考模型系统(Sr): L=[20.085 5-11.150 7]T,K1=[26.019 423.949 6],K2=[-24.699 5-24.699 5]. 图1 系统(S)真实状态和观测系统状态误差曲线Fig.1 Error curves between real state and estimated state of the system(S) 下面分别用参考输入信号r(k)为正弦信号和阶跃信号两种情况说明跟踪效果. 1) 当参考输入信号为正弦信号时: (26) 系统输出轨迹y(k)和参考输出轨迹yr(k)如图2所示. 图2 输入式(26)下的系统输出轨迹和参考输出轨迹Fig.2 Trajectories of system output and reference output for input (26) 2) 当参考输入信号为阶跃信号时: (27) 系统输出轨迹y(k)和参考输出轨迹yr(k)如图3所示. 图3 输入式(27)下的系统输出和参考输出的轨迹Fig.3 Trajectories of system output and reference output for input (27) 5结论 主要研究了具有多重时变时滞的离散时间系统基于状态观测器的H∞输出跟踪控制问题,其中参考信号由给定的参考模型生成,通过构造分段Lyapunov函数,结合Newton-Leibniz公式引入自由权矩阵并利用线性矩阵不等式分析技巧,得到跟踪误差系统满足指数稳定和H∞性能的一个时滞依赖的充分条件,并利用锥补线性化思想将非凸可行性问题转化为非线性规划的求解问题,通过MatlabLMI工具箱求得状态观测器和跟踪控制器.数值仿真验证了结论的有效性. 参考文献: [1]俞立.线性不确定多时滞系统的鲁棒镇定的研究[J].浙江工学院学报,1991(1):54-64. [2]俞立,杨马英,陈国定,等.不确定多时滞系统的无记忆鲁棒H∞控制器的设计[J].浙江工业大学学报,1998,26(2):148-153. [3]ZHANGDan,YULi. H∞outputtrackingcontrolforneutralsystemswithtime-varyingdelayandnonlinearperturbations[J].CommunicationsinNonlinearScienceNumericalSimulation,2010,15(11):3284-3292. [4]SUNHaibin,HOULinlin.Compositedisturbanceobserver-basedcontrolandH∞outputtrackingcontrolfordiscrete-timeswitchedsystemswithtime-varyingdelay[J].MathematicalProblemsinEngineering,2013,2013(2013):1-12. [5]SONGBo,PARKJUH,WUZhengguang,etal.Newresultsondelay-dependentstabilityanalysisandstabilizationforstochastictime-delaysystems[J].InternationalJournalofRobustandNonlinearControl,2014,24(16):2546-2559. [6]仇翔,滕游.离散时滞系统的网络化保成本控制[J].浙江工业大学学报,2014,42(4):400-404. [7]LIZhicheng,GAOHuijun,KARIMIHR.StabilityanalysisandH∞controllersynthesisofdiscrete-timeswitchedsystemswithtimedelay[J].Systems&ControlLetters,66:85-93. [8]ZUOLei,XUXin,LIUChunming.Ahierarchicalreinforcementlearningapproachforoptimalpathtrackingofwheeledmobilerobots[J].NeuralComputingandApplications,2013,23(7-8):1873-1883. [9]XULijie,WANGQiang,LIWei,etal.Stabilityanalysisandstabilizationoffull-envelopenetworkedflightcontrolsystems:switchedsystemapproach[J].IETControlTheoryandApplications,2012,6(2):286-296. [10]YANGYitao.RobustH2/H∞outputtrackingcontrolofuncertaindiscrete-timeswitchedsystemswithstatetime-delay[J].WseasTransactionsonMathematics,2013,12(7):798-807. [11]LIUMeiqin,CHENHaiyang,SHENGWeihua. H∞outputtrackingcontrolofdiscrete-timenonlinearsystemsviastandardneuralnetworkmodels[J].IEEEtransactionsonneuralnetworksandlearningsystems,2014,25(10):1928-1935. [12]FIGUEREDOLFC,ISHIHARAJY,BORGESGA,etal.RobustH∞outputtrackingcontrolforaclassofnonlinearsystemswithtime-varyingdelays[J].Circuitssystemsonsignalprocess,2014,33(5):1451-1471. [13]LIQingkui,ZHAOJun,LIUXiangjie,etal.Observer-basedtrackingcontrolforswitchedlinearsystemswithtime-varyingdelay[J].InternationalJournalofRobustandNonlinearControl,2011,21(3):309-327. [14]ZHANGHui,SHIYang,XUMinqiang,etal.Observer-basedtrackingcontrollerdesignfornetworkedpredictivecontrolsystemswithuncertainmarkovdelays[J].InternationalJournalofControl,2013,86(10):1824-1836. [15]ZHANGYongyou,ZHANGNi.GeneralizedH2filteringfordiscrete-timeswitchedsystemswithmultipletime-varyingdelays[J].AdvancedMaterialsResearch,2012,562:1646-1649. [16]GHAOUILE,OUSTRYF,AITRAMIM.Aconecomplementaritylinearizationalgorithmforstaticoutput-feedbackandrelatedproblems[J].IEEETransactionsonAutomaticControl,1997,42(8):1171-1176. (责任编辑:陈石平) Observer basedH∞output tracking control for discrete time systems with multiple time varying delays ZHANG Ni, FAN Yixin, HE Xiongxiong (College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China) Abstract:In this paper, observer based H∞output tracking control is investigated for discrete time systems with multiple time varying delays. The reference signal is generated by the reference model. Based on stability of Lyapunov, linear matrix inequality (LMI) technique and free-weighting matrices method, the delay dependent sufficient condition is derived for guaranteeing the exponentially asymptotic stability and H∞output tracking performance of discrete time systems with multiple time varying delays. The results are dependent on system delay with a less conservative. The nonlinear matrix inequality involved in the state observer and feedback controller design is transformed into nonlinear programming problem constrained by LMIs using the cone complementarity linearization algorithm. Finally, the simulation results are given to demonstrate the effectiveness of the proposed methods. Keywords:discrete time systems; multiple time varying delays; output tracking control; state observer; exponentially stability 文章编号:1006-4303(2015)04-0438-07 中图分类号:TP271+.9 文献标志码:A 作者简介:张霓(1970—),女,浙江杭州人,副教授,硕士生导师,研究方向为时滞切换系统鲁棒控制、移动机器人,E-mail:zn@zjut.edu.cn. 基金项目:国家自然科学基金资助项目(61473262) 收稿日期:2015-01-28