基于离散元法崩塌体动力破碎分析
2016-01-21孙新坡何思明于忆骅
孙新坡,何思明,于忆骅
(1.西南科技大学 土木工程与建筑学院,四川 绵阳 621010;2.中国科学院水利部成都山地灾害与环境研究所,四川 成都 610041)
基于离散元法崩塌体动力破碎分析
孙新坡1,何思明2,于忆骅1
(1.西南科技大学 土木工程与建筑学院,四川 绵阳 621010;2.中国科学院水利部成都山地灾害与环境研究所,四川 成都 610041)
摘要:在汶川大地震的影响下,西南地区山体破坏严重.岩质边坡几乎全部出现破坏,崩塌十分严重,产生了大量的崩塌体,堆积于洞口或缓坡地带;且上方陡坡残留大量震裂岩体,在余震和多雨、多风的天气下易产生崩塌,对公路产生威胁.采用离散元法对崩塌体模拟,通过对不同粘结强度的崩塌体动力破碎的影响进行的数值模拟研究.结果显示:崩塌体的粘结强度可以由离散元的平行键强度来模拟,不同粘结强度对崩塌体的运动和堆积形态有重要影响,再现了崩塌体破碎动力演化过程.为崩塌体破碎和防御提供理论依据.
关键词:崩塌;离散元方法;PFC;破碎
国内西南地区滑坡崩塌灾害非常严重,并具有突发性,给公路沿线交通重大生命伤害和财产损失.岩崩灾害运动过程中不断破碎,研究崩塌的动力破碎机理具有很重要的现实意义,国外方面,多年来大量学者[1-6]对崩塌灾害破碎方面进行了研究.何思明等[7]分析了强震荷载下裂缝岩体拉剪破坏机理.裴向军等[8],运用非连续变形数值分析(DDA)方法,对危岩体在强震作用下的失稳模式、破坏规模、运动轨迹及对桥墩冲击的动力响应进行模拟研究.裴向军等[9]以汶川地震未扰动现场滚石痕迹的判识、测量取样及分析,得出强震作用下块体(石)是以一定初始速度抛射而出的;其坡面运动表现为滑动、滚动、跳跃与3种方式的组合.杨伟等[10]针对顺层滑坡的特点,采用ARCGIS集成的VBA开发环境,提出了一种三维折线法分析边坡的稳定性.
笔者以龙洞子出口危岩体为研究对象,在详细地质调查的基础上,运用离散元法对崩塌体动力运动和破碎过程进行模拟预测,为崩塌防治设计提供理论和技术支持.
1数值模型及参数确定
1.1问题描述
龙门山地区位于青藏高原东部边缘与扬子地台西部边缘的接合部.由3条断裂带构成,构造非常复杂.发生过多次七级以上的地震.地质环境是脆弱,岩体破碎;在气候上,夏季局部降雨非常集中.
2008年5月12日映秀发生了8.0级大地震,震中位于映秀的龙门山中央断裂带,隧道位于震中附近(图1),且隧道出口仰坡地段为抗震不利地段.在汶川大地震的影响下,龙洞子隧道出口仰坡破坏严重(图2).岩质边坡几乎全部出现破坏,崩塌十分严重,产生了大量的崩塌体,堆积于洞口或缓坡地带;且上方陡坡残留大量震裂岩体,在余震和多雨、多风的天气下易产生崩塌,对公路产生威胁.
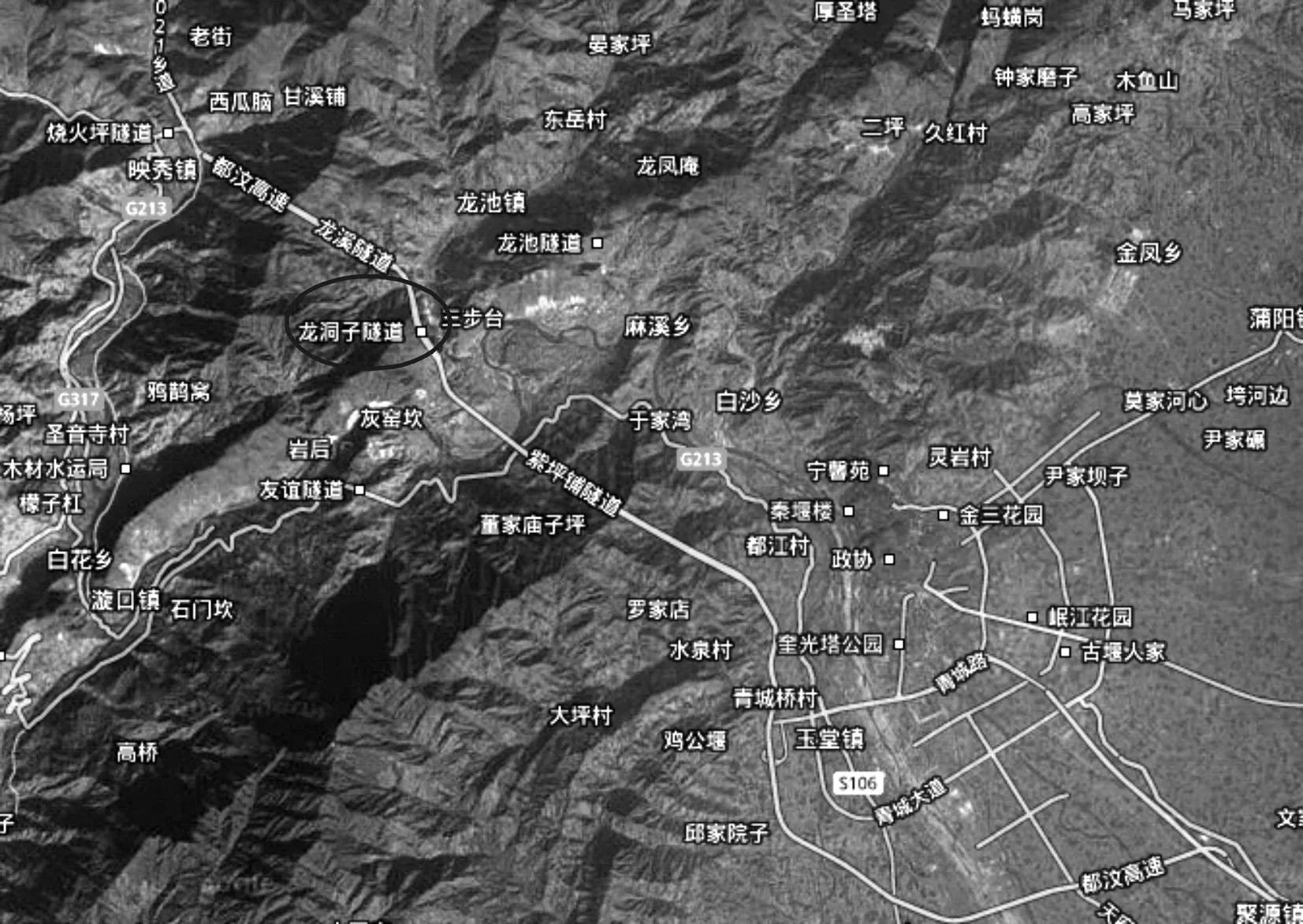
图1 龙洞子隧洞位置Fig.1 The location of Longdongzi tunnel
距洞口内侧80 m处裸露的石灰岩陡崖、陡坡靠近白岩山背斜轴,岩层近直立至局部倒转,岩体节理发育,加之该地段处于当地石灰窑厂开挖石灰岩矿放炮崩落带,岩体表层松动,卸荷裂隙发育,已形成一宽60 m,高约90 m的崩塌危崖段.陡坡中部并见长度大于20 m,宽达0.5 m的大裂缝.崩塌段平时亦有飞石落下,逢暴风雨时崩塌更加剧烈.图3为龙洞子隧道出口处崩塌横截面图,见图2直线标示.

图2 龙洞子隧洞出口崩塌Fig.2 The landslide occurring around the exit of Longdongzi tunnel

图3 龙洞子隧洞出口崩塌剖面图Fig.3 The section diagram of landslide located in Longdongzii tunnel exit
1.2模型概况
根据现场调查和实地勘测,龙洞子隧洞计算初始构型如图4所示,其中模型相对高差680 m,水平距离为166 m.
在数值模型中:崩塌体由颗粒模拟,坡面由刚性墙模拟,如图4所示.崩塌体通过颗粒体模拟,在整个变形区域内随机生成由粒子质量构成崩塌体,滑动面用“墙单元”模拟.崩塌体体积为133 m3,总颗粒数为180 个.采用颗粒半径范围从0.28 m到0.56 m,服从高斯分布.崩塌体与坡面的接触是球体与刚性面接触,微观为线性接触,宏观可以表现非线性.假设崩塌体与坡体底部有个破裂面.崩塌体与坡面之间有法向接触力和切向摩擦力,无粘结力.
1.3参数选取
在离散元法中,微观参数与平时常见的宏观参数没有直接对应关系.必须进行双轴或者三轴试验数值试验或者其他数值试验进行校核来确定微观参数,如表1所示.
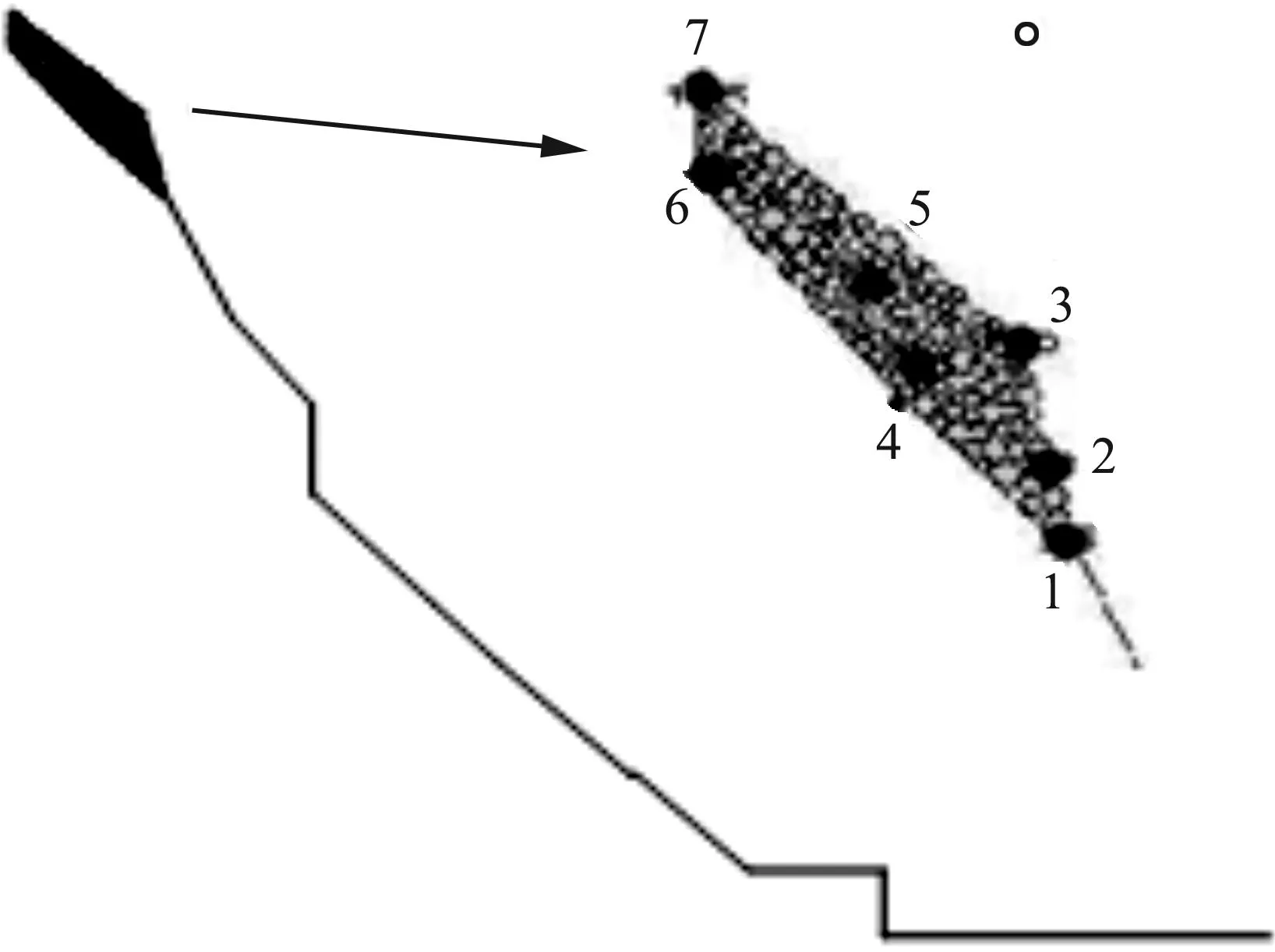
1~7—编号的监测球图4 龙洞子崩塌数值模型Fig.4 Numerical model of Longdongzi collapse

颗粒法向刚度/MPa100平行键切向强度/GPa48.0,16.0,5.3颗粒切向刚度/MPa25坡底摩擦系数0.15坡底法向强度/MPa107颗粒最小半径/m0.28坡底切向强度/MPa107颗粒最大半径/m2.00平行键法向强度/GPa48,16,5.3颗粒间摩擦系数0.50
1.4地震波输入
在模型中施加了一个水平向的地震波,施加位置为整个坡体底部,时间为20 s,如图5所示.

图5 地震动加速度时程Fig.5 The ground motion acceleration time history
2结果分析
图6是崩塌体在重力作用下逐渐破坏的全过程.崩塌体外围颗粒由于不受约束,在边坡上运动,碰撞,有些直接越过拦石墙,最后到达路面上.更多的碎屑体在拦石墙前堆积,颗粒面抬升,最后达到拦石墙高,且有些颗粒越过拦石墙,堆积到路面上.
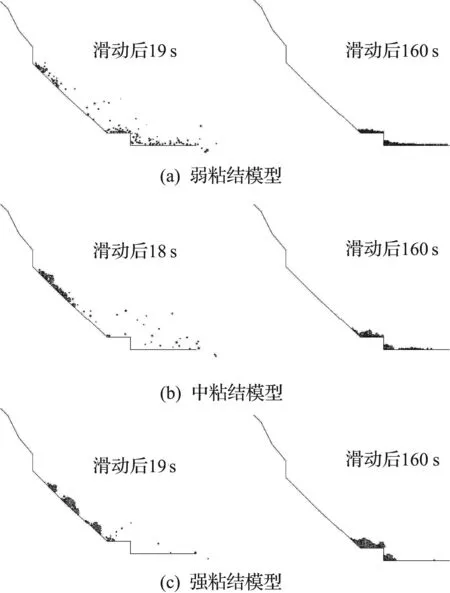
图6 粘结强度对崩塌运动堆积形态的影响Fig.6 The influence of bond strength to accumulation of the collapse movement
2.1不同粘结强度的崩塌演化
粘结强度对崩塌体崩塌滑动有明显的影响.图6显示结果不同粘结强度的崩塌体的崩塌滑动.这些模型为三种粘结强度分别为强、弱和中等.
在“强粘结强度模型”,其主体质量行为大致颗粒作为刚性块向下滑动和跨越洞口堆积到公路上,大部分的滑块到达公路之前不破坏.在“弱等强度模型”、主体到达底部前变得支离破碎成小块.在模拟器里,所有上层的粒子翻滚和碰撞,最终被掩埋.在“中等强度模型”,部分完全破碎,部分为破碎.
2.2不同粘结强度的崩塌体的破碎演化
平行键来模拟岩体的粘结强度.图7显示平行键破碎百分比随时间变化.为“弱强度模型”,滑动的大约20 s大约85%的平行键破坏:滑动50 s后几乎所有平行键都破坏了.在这种情况下平行键在崩塌体达到公路上前全破坏.因此,滑块在滑动过程中变得支离破碎.在这一阶段,粘性颗粒的行为近似为一种流体.如上所述,该模型不能够解释实际崩塌的行为.考虑到的高强度模型的具有较强的粘结强度,滑块大约70 s时仍然很完整.这么较长时间跨度只有大约7%的平行键破损.70~20 s破碎显著增加,之后稳定.最终结果只有30%平行键破坏.关于“中等强度模型”,第一次粘结键键破坏发生显著增长近10 s,5%的粘结键破坏了.另一个显著增加大约在50 s,因为滑体和公路底部之间的碰撞.模型最大的破碎平行键是22%.中等强度特征模型较为合理的解释了崩塌体的粘结强度.

图7 不同平行键强度破坏对比Fig.7 Compare different parallel bond strength fracture
2.3崩塌体不同部位的颗粒运动
用弱强度模型分析运动距离,例子中用7个圆球监测(图8).球1,7的初始距离是29.8 m,堆积后两个靠在一起.滑动过程中,下坡的颗粒碰上后缘的颗粒,下坡的颗粒就会斜向下坡方向加速.
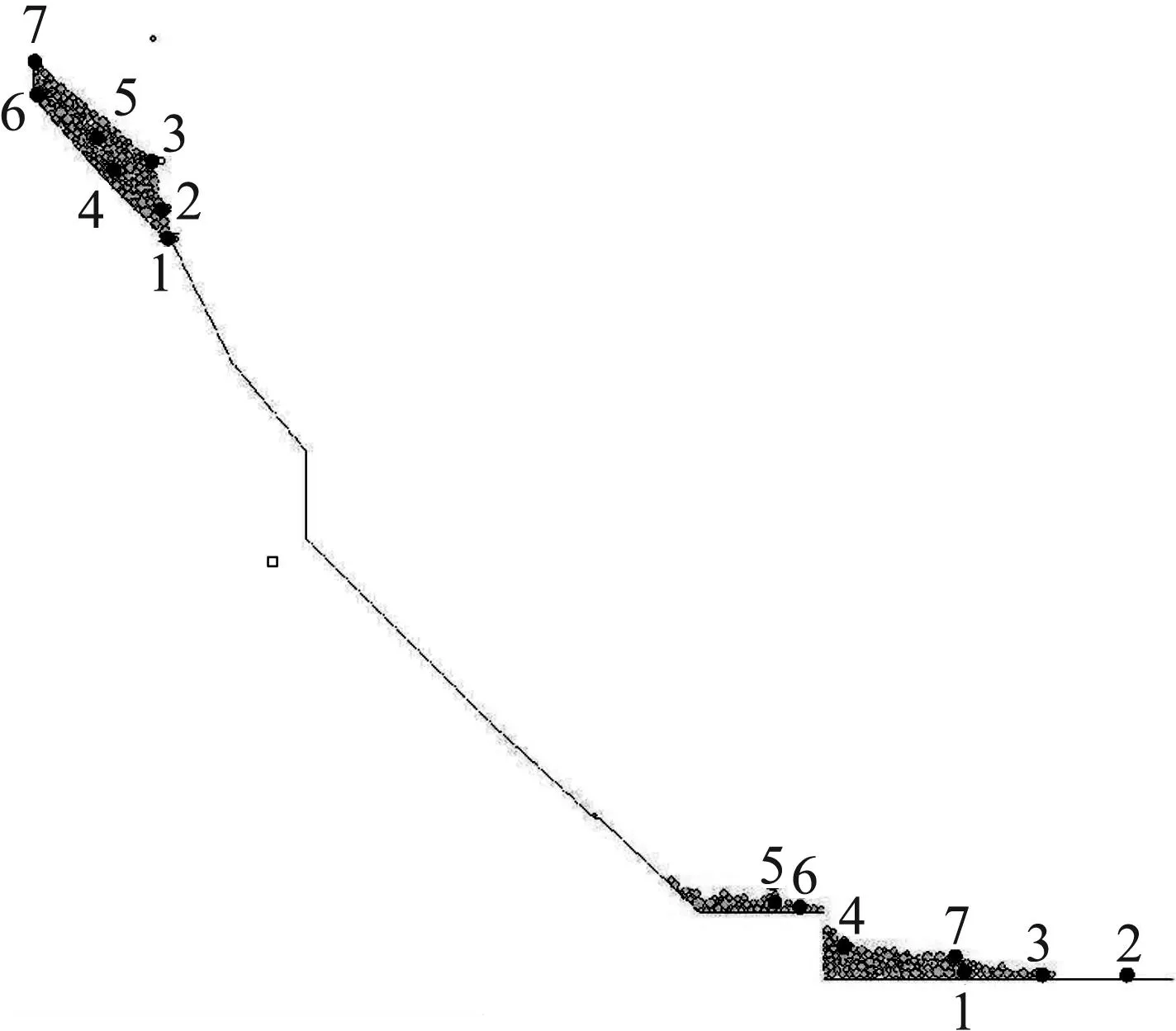
1~7—编号的监测球图8 对比崩塌体7个监测颗粒起始和最终堆积位置Fig.8 Comparison between original and final positions for ten monitored disks
如图8所示,分析崩塌体前缘附近3个圆球1,2,3.崩塌滑动前,球3在崩塌前面最上方,球2在前缘中间,球1在前缘最下方.滑动后,球2到最远处,球1相对最近,说明球3势能比球1大,运行距离远,球2说明收到了后面崩塌体的碰撞力,距离更远.滑动后,球2,7经历了大的位移(约170 m).这个例子显示崩塌前缘表面的块体在滑动过程中可能彼此超过并被掩埋,崩塌的接近基地的滑块移动距离明显小不会移动到表面.图8也显示了崩塌体的中部和上部的块体的位置经历了小的变动,比如球7,6,5.而崩塌体内部深层的块体可能改变(球4)或者移动距离小(崩塌基底附近的球4与球3,2相比).
某一深度块体的真实的位移不能检查,但是通过模拟可以确定崩塌体不同部位的堆积情况,如图8所示(如:球1,2,3,5,7).一般,下坡截面上的球比后缘的球移动距离远,上层的球比底层的球移动距离远.崩塌体表面和前部的颗粒由于不受约束,更容易滑动和滚动.
3结论
通过对龙洞子隧道出口处的崩塌体的离散元数值模拟,一系列不同参数模拟分析.结果表明:离散元在地震波作用下可以定性和定量模拟崩塌体的动力演化过程和堆积过程,并具有合理性;崩塌体在崩塌过程中,不同粘结强度对崩塌体的运动和堆积形态有重要影响.不同平行键强度的崩塌体可以模拟不同粘结强度的崩塌体,再现了崩塌体破碎动力演化过程;崩塌体表面的颗粒和前缘的颗粒运动距离远,内部颗粒和底部颗粒运动距离近.前缘颗粒和表面颗粒由于不受约束,有更大自由度,运行距离远;在运动过程中,内部颗粒和底部颗粒由于受到周围的颗粒约束,运行距离近.
参考文献:
[1]TANG C L, HU J C, LIN M L, et al. The tsaoling landslide triggered by the Chi-Chi earthquake, Taiwan: insights from a discrete element simulation[J]. Engineering Geology Engineering Geology,2009,70(3):1-19.
[2]PIERCE M, MASIVARS D, CUNDALL P A, et al. A syntheticrock mass model for jointed rock[C]//Proceedings of the first CA-US Rock Mechanics Symposium. Vancouver: Taylor & Francis,2007:341-349.
[3]POTYONDY D O, CUNDALL P A. A bonded-particle model for rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2004,41(8):1329-1364.
[4]HAO S, LIU W K. Moving particle finite element method with superconvergence:nodal integration formulation and applications[J]. Computer Methods in Applied Mechanics and Engineering,2011,195(44/47):6059-6072.
[5]RABCZUK T, BELYTSCHKO T. A three dimensional large deformation meshfree method for arbitrary evolving cracks[J]. Computer Methods in Applied Mechanics and Engineering,2007,196:2777-2799.
[6]RABCZUK T, SAMANIEGO E. Discontinuous modelling of shear bands using adaptive meshfree methods[J]. Computer Methods in Applied Mechanics and Engineering,2008,197:641-658.
[7]何思明,吴永,李新坡.强震荷载下裂缝岩体拉剪破坏机理[J].工程力学,2012,29(4):178-184.
[8]裴向军,黄润秋,李世贵.强震崩塌岩体冲击桥墩动力响应研究[J].岩石力学与工程学报,2011,30(9):3995-4001.
[9]裴向军,黄润秋,裴钻,等.强震触发崩塌滚石运动特征研究[J].工程地质学报,2012,19(4):498-504.
[10]杨伟,丁伯阳,潘晓东,等.基于GIS的边坡三维稳定性计算[J].浙江工业大学学报,2012,40(1):92-95.
(责任编辑:陈石平)
Dynamic crush analysis of collapse bodies based on the discrete element method
SUN Xinpo1, HE Siming2, YU Yihua1
(1.School of Civil Engineering and Architecture, Southwest University of Science and Technology, Mianyang 621010, China;
2.Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu 610041, China)
Abstract:Owing to the influence of the Wenchuan earthquake, mountains in the southwest of China were seriously destroyed. Almost all rock slopes were damaged and the collapse was very serious, producing a large amount of collapse bodies at the mouth of caves or in gentle slope zones. There were a large mount of cracked rocks in the upper steep slopes. Under the conditions of aftershock, and rainy and windy weather, these rocks are easily collapsed, threatening the safety of highways. A numerical simulation is conducted on the dynamic crush of collapse bodies with different bond strengths by the discrete element method. The results show that the bond strength of collapse bodies can be modeled by the parallel bond strength designed in the discrete element method. The bond strength has important influence on the movement and accumulation of collapse bodies, and the evolution process of the dynamic crush of collapse bodies is reproduced, which provides a theoretical guidance for the defense of collapse bodies.
Keywords:collapse; discrete element method; crush
文章编号:1006-4303(2015)04-0464-04
中图分类号:X4
文献标志码:A
作者简介:孙新坡(1978—),男,河北保定人,讲师,博士,主要从事山地灾害形成机理及防治技术研究,E-mail:xinpo2008@sina.com.cn.
基金项目:国家自然科学基金资助项目(41472325);西南科技大学博士基金资助项目(12zx7124);绵阳市科技局项目(14Q0013)
收稿日期:2014-10-30