中国股市收益率与异质波动性关系研究

中国股市收益率与异质波动性关系研究

王春峰1，张驰1，房振明2

(1.天津大学管理与经济学部，天津300072；2.渤海证券股份有限公司，天津300381)

摘要：本文研究了中国股票市场的异质波动性问题。主要从异质波动性的识别与分布，异质波动性与股票收益率之间的关系，以及异质波动性是否被充分定价等三方面进行探讨。研究的目的在于分析股票异质波动性问题在中国股票市场中的特殊地位，这其中也包括异质波动性对股票收益影响问题。结合中国股票市场的数据，采用广义矩估计(GMM)的数量方法，显著地得到了中国股票市场中异质波动性水平，并以此分析了异质波动性与股票收益之间的关系，证明股票异质波动性水平是投资者进行决策时需要考虑的重要因素之一。

关键词：金融工程；异质波动性；广义矩估计；股票收益率；风险溢价

收稿日期：2014-02-13

基金项目：国家自然科学

作者简介：王春峰(1966-)，男，河北隆尧人，博士研究生，教授，博士生导师，研究方向：金融工程与资本市场;张驰(1986-)，男，天津人，博士研究生，研究方向：证券市场微观结构;房振明(1976-)，男，辽宁锦州人，博士研究生，副教授，研究方向：金融工程与金融投资。

中图分类号：F830.91文章标识码：A

A Study on the Relationship between the Chinese Stock Market

Returns and Idiosyncratic Volatility

WANG Chun-feng1, ZHANG Chi1, FANG Zhen-ming2

(1.CollegeofManagementandEconomics,TianjinUniversity,Tianjin300072,China; 2.BohaiSecuritiesCo.,Ltd.,Tianjin300381,China)

Abstract:This paper studies the problem of idiosyncratic volatility in Chinese stock market. There are three problems discussed in this paper. They are the identification of an idiosyncratic volatility, the relationship between the idiosyncratic volatility and stock returns and pricing problem. The purpose of this study is to find the status of the idiosyncratic volatility in Chinese stock market, including the pricing and stock return two problems. In the empirical research, combined with Chinese stock market data, we use the statistical method of generalized moment estimation(GMM)to get the idiosyncratic volatility and we analyze the relationship between the stock returns and idiosyncratic volatility. At last we find that the idiosyncratic volatility is not priced in Chinese stock market. Moreover, there is no correlation between the idiosyncratic volatility and stock return. Thus, when the investors want to make a decision, they should consider the influence of idiosyncratic volatility adequately.

Key words:financial engineering; idiosyncratic volatility; GMM; stock returns; risk premium

0引言

对于投资者来说，增加收益减小风险是一个永恒不变的目标，大量的研究也围绕着这一主题展开。二十世纪中叶，美国经济学家William-Sharpe提出了资本资产定价模型(CAPM)。此后，CAPM一直作为主流的资产定价模型来衡量资产的风险和回报之间的关系[1～4]。Merton提出一个不同观点，如果一个市场投资者因为某种原因不能持有一个风险完全分散的市场投资组合，则市场上的其他投资者也不能持有一个风险完全分散的投资组合，因此CAPM模型在理论假设上是不成立的，导致这一结论的原因就是资产存在异质波动性[5]。Malkile和Xu通过实证研究证明了Merton的结论，异质波动性确实存在并且与收益率之间有着很大的联系，同时他们认为股票异质波动性所带来的超额回报可以被看作是投资者对市场上某种投资产品供需不平衡的一种补偿[6,7]。

有关股票异质波动性的研究有三组美国学者有着巨大的贡献。Malkiel和Xu认为股票的异质波动性和股票回报率之间成正比，股票收益随着股票异质波动性的增大而提高反之则随着股票异质波动性的降低而减小。而在同一时间Ang等人却提出了与之完全相反的结论，他们认为股票的异质波动性和股票回报率之间是负相关的关系，即异质波动性高的股票的收益反而要比异质波动性低的股票的收益率要低[8]。与这两组学者观点都不相同的是Bali等人提出股票的异质波动性和股票回报之间没有任何关系[9]。在研究方法上Bali等人先是肯定了Malkiel和Xu的发现，在这基础之上延长了Malkiel和Xu的研究时间后才提出了他们自己的结论。以上三组学者的研究成果都是基于美国市场，虽然他们在异质波动性与股票收益率关系问题上存在分歧，但是在异质波动性这个主要问题上已经代表了当今主流的研究成果[10～12]。

国内对异质波动性的研究尚处于起步阶段。赖步莲等研究了股票异质波动性与上市公司并购的关系[13]。孔东民等探讨了异质波动性究竟是一种自燃避险行为还是源自信息不确定的问题[14]。苏明政，张庆君研究了异质波动条件下中国股市与国际股市的联动问题[15]。但是这些研究基本停留在定性研究和宏观研究层面，没有分析异质波动性与中国股票市场的内在联系，处于什么地位等问题。研究中国资本市场异质波动性与股票收益率之间的关系具有重要的实际意义，搞清楚中国股市是否存在异质波动性及其大小的问题可以帮助我们更好的了解中国股票市场的特性。而研究异质波动性与收益率之间的关系可以帮助投资者调整自己的资产组合，如果不考虑异质波动性对收益率的影响就有可能使投资者承担过多的风险甚至影响到整体投资的成败。

1考虑异质波动性的股票收益率模型

1.1股票收益率的对数随机微分方程

本文利用随机游走的基本思想建立带有异质波动性的股票收益率模型。早在二十世纪初，学者Bachelier在论文中就指出股票的价格行为是一种随机游走的过程

dS=μSdt+σSdX

其中S为股票价格，S的预期漂移率为μS，σ为标准差。假设F(S)=logS，这个假设的优点在于避免了出现股票价格为负的情况。

在本文中记Mt表示t时刻的市场指数，则市场指数满足方程

(1)

μm表示漂移率，满足

μm=r+δσm

(2)

(3)

μi表示漂移率，满足

μi=r+δβiσm+γiσi

(4)

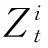
1.2模型的理论分析

1.3模型的转化与求解

本文建立模型的基础是包含布朗运动的随机微分方程，即伊藤过程。一般的平滑函数是可微的，只要知道某一点的斜率，就可以预测函数下一步的函数值。而布朗运动是不可微的，找不到斜率也不可预测。由于布朗运动有这样的特性，正好可以应用于股票模型上。由于资产的价格可以写成布朗运动的函数，这表示资产价格也有不可预测的成分在里面，并且它的轨迹也是非常不规则的。代表市场指数的模型(1)中随着不可预测信息的披露，Mt的下一个瞬间增量为dMt。这个增量来自于两个部分，一部分是确定项，另一部分是随机项，由于这部分的增量来自于布朗运动的增量，而我们知道布朗运动是不可微的，因此Mt的瞬间增量的方向基本上也是不可预测的。代表个股价格的模型(3)也有着同样的特性。

伊藤过程在时间上是连续的，但却是不可微的，因为它是布朗运动的函数，而布朗运动是不可微的，因此要处理这个问题必须应用随机微积分，而其中最重要的部分就是伊藤引理，这里要运用它将不能直接估计的(1)(3)式转化成可以估计的一般方程。

对(1)式应用伊藤引理，得到

解微分方程得到

(5)

其中ΔT表示两个时间点的间隔，若全部观测时长为T，从中选取n个时间点，则有ΔT(n-1)=T。同理由(3)式可以得到

(6)

至此，由式(5)(6)与式(2)(4)构成的模型是可以进行估计的。

在模型参数的估计方法上，传统的计量经济学估计方法如普通最小二乘法、工具变量法和极大似然法等都存在自身的局限性，即其参数估计量必须在满足某些假设时才是可靠的估计量。而GMM不需要知道随机误差项的准确分布信息，允许随机误差项存在异方差和序列相关，因而所得到的参数估计量比其他参数估计方法更有效。因此，GMM方法在模型参数估计中得到广泛应用。由于布朗运动项Wt的存在会导致一只股票收益率数据存在序列相关性，这在模型参数估计上造成了困难也使得常用的最小二乘法失效。因此，本文采用广义矩估计(GMM)的方法保证了参数估计有效性与一致性。

1.4广义矩估计(GMM)过程

记θ=(σm,γi,βi,σi)′为待估计参数向量，定义函数

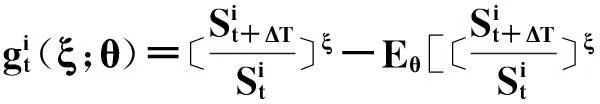
(7)

其中ξ是一个实数，ξi(i=1,2,…,k)构成了矩向量ξ=(ξ1,ξ2,…,ξk)′，Eθ[·|·]表示参数向量取θ时的条件期望(条件期望具体表达式见附录)。

对于k个矩条件，则有函数向量

(8)

由此可以得到GMM的目标函数

(9)

2模型参数估计与实证分析

2.1样本数据的选取与分析

本文以沪深300指数作为基本的市场指数，定义个股异质波动性为除去沪深300指数成分股之外的个股特有的波动性。这种假设的原因在于沪深300指数的编制目的就是为了反映中国证券市场股票价格变动的概貌和运行状况，且指数行业分布状况基本与市场行业分布比例一致，可以很好地代表整个市场的变化情况。除此之外，个股特有波动性保证了异质波动性独立于其他风险之外，比如行业风险等。

本文选取2012～2013两年间中国大陆股票市场中股票日收益率作为基本数据。由于市场指数是连续的，如果股票连续交易时间过短会导致与市场指数无法很好地匹配，但如果要求的连续交易天数过多又会导致选取的样本过少。因此选取除去成分股外，在每年内连续交易时间均超过240天共1366只股票作为含有异质波动性的个股样本进行模型参数估计，这样在保证了股票数据与指数数据匹配的同时，也保证了样本的数量。

2.2实证结果分析

选择合适的矩条件向量是GMM方法的重要步骤之一，在选择时应考虑矩条件的对称性、模型参数数量、矩之间的变化幅度以及模型估计收敛速度等多方面原因。例如Khovansky等[16]在研究中尝试了ξ=(-1.5-1-0.50.511.52)′等多个向量作为矩条件。在经过多次尝试和比较后，本文选取向量ξ=(-1.5-111.522.5)′作为条件向量并得到参数估计结果如下。

表1　参数估计显著性统计结果

注：表中数字代表显著的股票数量。

从表1中可以看出市场风险σm完全显著同时βi的显著性也比较高，这证明个股确实均受市场风险的影响。此外，异质波动性显著性很高说明中国股票市场中显著存在异质波动性，但同时异质波动性溢价的显著性对于总数1366只股票来说并不是很高。依据参数性质我们进一步做了下面不同参数组合的显著性统计：

表2　参数组合显著性统计

注：表中数字代表显著的股票数量。

这里的“+”并不是指数学上的相加，而是指多个参数同时显著的情况。与市场风险有关的σm+βi同时显著性良好，添加市场波动性后σm+βi+σi同样有较高的显著性，但在加入溢价项后σi+γi和σm+γi+βi+σi显著性明显降低。通过表1和表2中的结果我们可以看出中国股票市场上确实显著存在异质波动性，并且这种异质波动性可以通过模型(1)～(4)识别出来。

下面讨论异质风险是否被有效定价的问题。各参数的具体估计统计结果见表3。

表3　参数估计结果统计特征表(90%显著水平下)

从结果中我们看到市场波动性σm的标准差相对较小，整体分布如图1，从图上我们看出除了个别股票市场波动性比较分散外，绝大多数个股的市场波动性是一致的，基本都在0.17左右。这印证了我们在第3章中的假设，即便作为未知参数重新估计市场波动性σm，所有个股所分摊的市场风险也是相同的。因此我们不认为σm“因股而异”，而是对于同一个市场来说是一个常数，在这里σm≈0.1701。这也从一个侧面证明了模型是有效的。

图1　市场波动性估计结果分布图

图2　个股异质波动性结果分布图

同样标准差相对比较小的异质波动性σi估计出的结果却和市场风险不同，如图2，与个股承担的相同市场风险不一样的是个股的异质波动性完全不同，因此个股的σi是“因股而异”的。

根据图3可知中国股市中异质波动性满足一个偏态分布，而且中国股市中异质波动性较小的股票要明显多于异质波动性较大的股票。

图3　异质波动性频度图

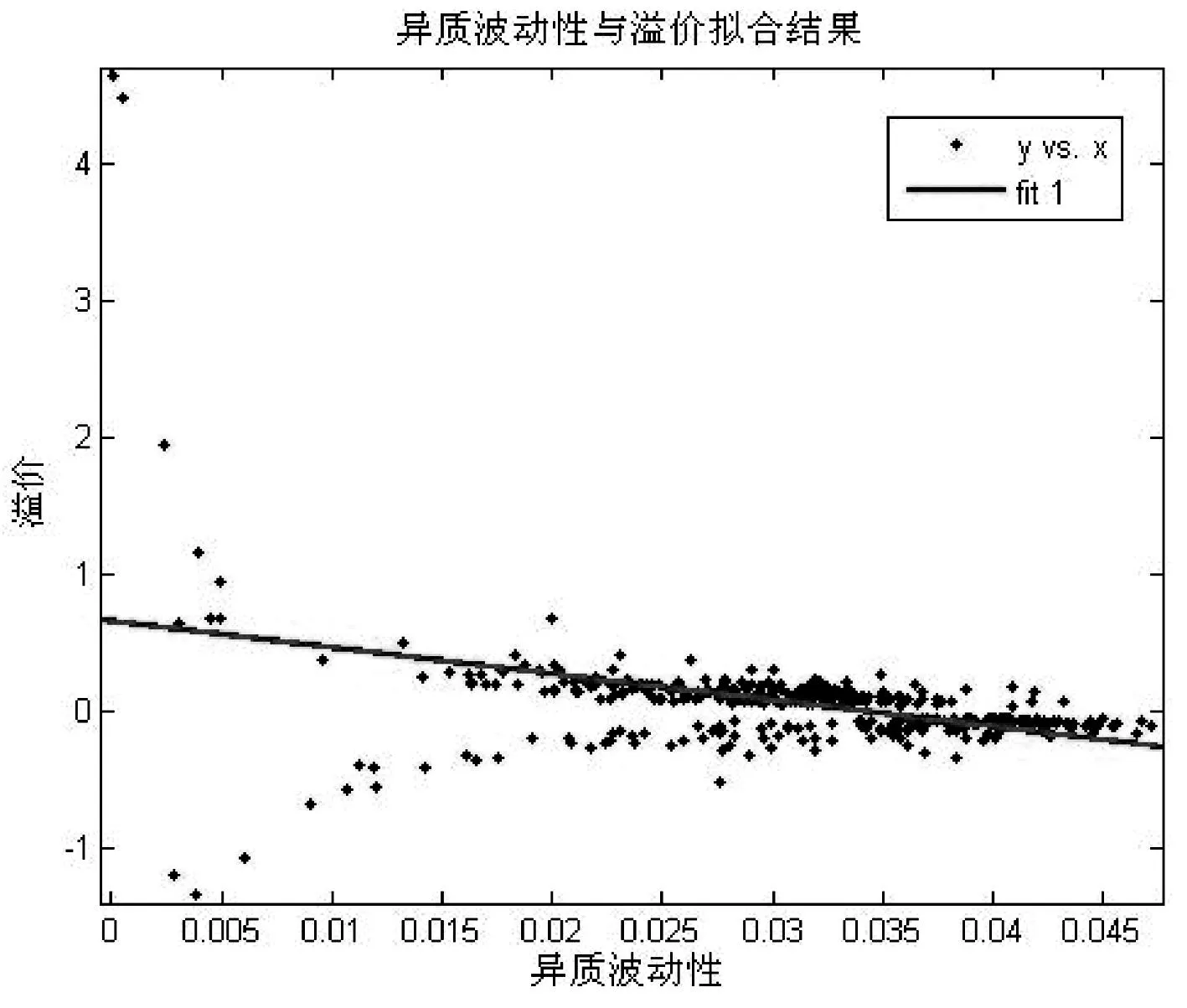
图4　异质波动性与溢价线性拟合结果(90%显著性409只股票)　　　

我们选取异质波动性与溢价共同显著的409只股票(90%显著性水平下)分析他们之间的相关性。结果见图4：从图上我们可以看出，异质波动性越小其带来的溢价波动性越大，而异质波动性越大其溢价越集中并且数值越小。从整体上看这是一个负相关的趋势，但是为了能够更直观的了解它们之间的线性关系，我们对数据做了线性拟合检验，图4中的直线就是拟合出的直线方程，具体拟合结果见表4。

表4　异质波动性与溢价拟合结果

从参数估计和拟合结果来看，中国股票市场中异质波动性与收益率之间并没有严格的相关关系，首先是异质波动性带来的溢价估计显著性不够高，其次虽然从整体上看异质波动性溢价有随着异质波动性减小而减小的趋势(图4)，但是从拟合结果来看(表4)，拟合优度比较低，因此不能说明溢价随着异质波动性减小而减小。

3结论

综上所述，在中国股票市场中确实存在异质波动性，但是目前的市场上并没有对这个因素进行有效的定价。同时，异质波动性与收益率的变化并没有严格的相关关系，不能认为在中国市场上股票的收益率随着异质波动性的增加而上升或者下降。对风险的定价就是对一种风险要求的价格补偿。而异质波动性因素没有被定价，造成这一现象的原因与中国股票市场的特点有着必然的联系。异质波动性相对于普通波动性而言有着更强的随机性和不可预测性，其中很大一部分来源于中国股市的信息不对称与不确定性。同时，中国股票市场的“T+1”交易模式影响了股票异质波动性及时反映到其价格上的效率，从而影响了异质波动性的定价能力。因此，对于一个金融机构来说，应该充分考虑如何对资产的异质波动性有效定价；而对于持有了一个资产组合的投资者而言，为了提高资产的收益或者为了规避不必要的风险，股票的异质波动性也是一个不能不考虑的重要因素。

参考文献：

[1]William S. Capital asset prices——a theory of market equilibrium under conditions of risk[J]. Journal of Finance, 1964, 19(3): 425-442.

[2]Banz W. The relationship between return and market value of common stocks[J]. Journal of Financial Economics, 1981, 9(1): 3-18.

[3]Bauman S, Dowen R. A fundamental multi-factor asset pricing model[J]. Financial Analysts Journal, 1986, 42(4): 45-51.

[4]Bauman S, Dowen R. The relative importance of size neglect[J]. The Journal of Portfolio Management, 1986, 12(3): 30-34.

[5]Merton, Robert C. A simple model of capital market equilibrium with incomplete information[J]. Journal of Finance, 1987, 42(3): 483-510.

[6]Malkiel B, Xu Y. Risk and return revisited[J]. The Journal of Portfolio Management, 1997, 23(3): 9-14.

[7]Malkiel B, Xu Y. Idiosyncratic risk and security returns[R]. Working Paper, University of Texas at Dallas, 2006.

[8]Ang A, Robert J, Xing Y H, Zhang X Y. The cross-section of volatility and expected returns[J]. Journal of Finance, 2006, 61(1): 259-299.

[9]Turan G, Nusret C, Yan X M, Zhang Z. Does idiosyncratic risk really matter[J]. Journal of Finance, 2005, 60(2):905-929.

[10]Goyal A, Santa-Clara P. Idiosyncratic risk matters[J]. Journal of Finance, 2003, 58(3): 975-1008.

[11]Berrada T, Hugonnier J. Incomplete information, idiosyncratic volatility and stock returns[J]. Journal of Banking and Finance, 2013, 37(2): 448-462.

[12]Athanassakos G. Are negative and ratio firms different[J]. Journal of Business and Financial Affairs, 2013, 2(1): 1-4.

[13]赖步连,杨继东,周业安.异质波动与并购绩效——基于中国上市公司的实证研究[J].金融研究,2006,318(12):126-139.

[14]孔东民,杨薇.产品市场竞争和异质波动：“自然避险”还是“信息不确定”?[J].产业经济评论,2012,11(2):1-37.

[15]苏明政,张庆君.异质波动条件下中国股市与国际股市联动性的动态分析——基于DCC-MVGARCH模型的实证研究[J].渤海大学学报(自然科学版),2013,34(9):328-334.

[16]Khovansky S, Zhylyevskyy O. Impact of idiosyncratic volatility on stock returns: a cross-sectional study[J]. Journal of Banking and Finance, 2013, 37(8): 3064-3075.