应急物资政企联合储备合作机理研究

应急物资政企联合储备合作机理研究

艾云飞，吕靖，王军，张丽丽

(大连海事大学交通运输管理学院，辽宁大连116026)

摘要：针对一些应急物资，采用政府企业联合储备方式储备，可以降低政府储备成本，企业也可以从中获益。本文研究政企联合实物储备的合作机理,分析了联盟参与人之间的博弈关系，建立了联盟收益模型，运用shapley值解决合作的联盟收益分配问题，最后分析了联盟的稳定性。算例分析显示在政企合作联盟中政府和企业关系类似“地主”和“农民”的关系,当企业获得的收益小于其机会成本时，企业不愿意加入联盟，这时政府需对企业进行交叉补贴来维持联盟稳定。缺货成本低于政府储备成本时，政府会考虑与企业联合储备或者选择缺货；缺货成本低于企业储备成本时，政府选择缺货。

关键词：管理科学与工程；政企联合；合作机理；博弈；shapley值；应急物资储备

收稿日期：2013-12-02

基金项目：保障我国海上通道安全研究(11JZD049);中央高校基本科研业务费专项资金资助(3132014311-1)

作者简介：艾云飞(1987-)，男，博士研究生；吕靖(1959-)，男，硕士，教授

中图分类号：X951 X915.4 文章标识码：A

The Study of Cooperation Mechanism between Government and

Enterprises in Emergency Supplies Reserve

AI Yun-fei, LV Jing, WANG Jun, ZHANG Li-li

(SchoolofTransportationManagement,DalianMaritimeUniversity,Dalian116026,China)

Abstract:For some kind of emergency supplies, the joint of government and enterprises can reduce the cost of government, and the enterprises can also benefit from it. This paper studies the mechanism of cooperation between government and enterprises in emergency supplies reserve. First it analyses the game between the alliance participants; then it uses the shapley value to solve the revenue distribution problem in the alliance; finally it analyses the stability of the alliance. The example analysis shows that the relationship between the government and enterprises in the alliance is similar to the relationship between “landlords” and “peasants”; the enterprises are reluctant to join the alliance when the earnings they gain are less than their opportunity cost, the government needs to cross-subsidize enterprises to maintain the stability of the alliance. When the shortage cost is less than the cost of government reserve, the government will choose shortage or join with the enterprises. When the shortage cost is less than the cost of enterprise reserve, the government will choose shortage.

Key words:management science and engineering; the joint of government and enterprises; the mechanism of cooperation; games; shapley; value emergency supplies reserve

0引言

随着地震、洪水等自然灾害的频繁发生，应急管理问题成为近年研究的热点。应急物资储备问题发生于应急管理的预防阶段，政府应急物资实物储备需要投入大量人力、物力。对于一些时效性高、不易存储的应急物资，如药品、食物，企业储备可以采取市场销售方式更新库存，大大减少因失效或者过期导致的损失。政府和企业如果能够联合储备，可以降低政府储备成本，企业也可以从中获益。

针对预防阶段应急资源储备问题，Chen tao[1]2011年系统的分析了中国救灾物资储备体系，将中国灾害应急储备分为国家储备、紧急补充、社会捐赠三个部分，其中国家储备包括政府储备和政府企业联合储备两个部分，政府企业联合储备又包括企业生产能力储备和企业实物储备。张自立[2]2008年研究了应急物资生产能力储备的协议企业选择问题，政府通过补贴促使企业拓展生产能力，在应急经费约束下，政府在其它物资储备和生产能力储备中做出选择，提高资金的支出效率。张自立[3]2010年在其博士论文中深入分析了企业剩余生产能力动员、生产能力代储以及生产能力储备共同投资建设等生产能力储备的实现途径。丁斌[4]2011年针对政府与供应商联合实物储备问题，研究政府提前支付供应商货款比例下，供应商如何确定应急物资的存储策略，从合作博弈角度确定联盟的合作期限与政府提前支付货款的比例。丁斌[5]2011年针对政企联合储备问题，分析企业和政府分别储备应急物资时各自的成本，在需求量是随机变量情况下，建立了不同储备形式下的成本函数，寻找出成本最低的储备方式，利用合作博弈理论解决企业储备时政府和企业成本的分摊。王军[6]2011年在其博士论文中对水上救援资源系统优化配置机理进行分析，包括外部性与资源配置方式的选择、协同配置动因与稳定性、协同配置条件下的成本分摊、联盟参与人可变的成本分摊等四个主要方面。

综上所述，以往学者针对政企联合储备合作机理的研究得不多。本文基于前人研究成果，研究政企联合实物储备的合作机理。分析了联盟参与人之间的博弈关系，建立了联盟收益模型；运用shapley值解决合作联盟的收益分配问题，并分析了联盟的稳定性；最后针对问题做了算例分析。

1问题描述

1.1上层非合作博弈分析

本文的研究主要针对应急物资实物储备，联盟参与人有政府和企业，参与人均有两种策略可供选择，即是否加入联合储备联盟。问题可以划分为上下两层博弈，首先上层博弈为一个完全信息静态非合作博弈，博弈的收益矩阵如表1所示。

表1　上层博弈收益矩阵

1.2下层合作博弈

如果上层博弈参与人选择形成联合储备联盟，下层形成一个合作子博弈，合作联盟如图1所示。

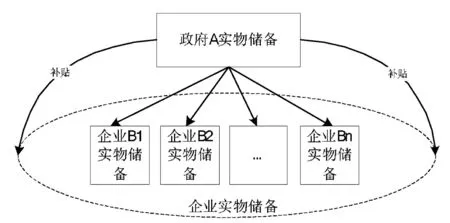
图1　合作联盟

合作联盟之所以能够形成，是因为政府通过政企联合实物储备可以降低成本，企业通过联合储备可以获得额外的收益，达到1+1>2的效果，即获得一个“协同剩余”。假设应急物资实物储备中政府和各个合作企业的资源投入为X={x1,x2…,xn}，投入效果为f(x)，政企联合储备实现协同效应需要满足：

f(X)>(f(x1)+f(x2)+…+f(xn))

(1)

政企联合储备的协同剩余为：

Δf=f(X)-(f(x1)+f(x2)+…+f(xn))

(2)

2合作博弈模型建立

本文假设条件主要有：

(1)应急物资的储备成本由政府承担，收益在联盟参与人中分配；

(2)政企联盟的收益运用合作博弈方法进行分配；

(3)政府和企业都是理性人，且政府和企业处于同等地位；

(4)市场是完全竞争的，企业之间不会形成小联盟与政府议价。

2.1联盟收益模型建立

基于以上变量解释，在已知联盟参与人的情况下，建立联盟的合作收益模型，目标函数为：

maxZ=Q*(C2+(C1+C3)/T)-

(3)

需要满足的约束条件：

(4)

xi≤qj

(5)

xj≥0

(6)

j=1,2,…,Ji=1

(7)

(3)表示政企联盟的收益；(4)表示政府和企业的实物储备量不大于目标储备量；(5)表示企业联合储备的物资量不大于企业可以提供的储备能力；(6)表示企业联合储备的物资量非负；(7)参数的取值空间。

2.2联盟收益分配方法

目前对于合作博弈分配方法的研究已很多，Shapley[7]1953年提出的一种基于Shapley值的合作分摊模式；Owen[8]1977年提出n人可转移效用合作博弈的Shapley值，即Owen值；Straffin和Heaney[9]1981提出了不可分成本的平均分摊解。在多人合作博弈分摊方法中，利用shapley值法解决收益分配问题是一种比较公正、合理且行之有效的方法，本文采用shapley值解决政企联合实物储备的收益分配问题。

假设A为应急物资实物储备工作，S表示联盟参与人集合，若U为S的一个子集，f(A,U)则表示U人联盟完成工作A可带来的收益。fi(A)为参与人i在A工作中获得的收益，fj(A)为参与人j在A工作中应得的收益。本文政企联合实物储备满足应用shapley值的三个定义[10]。

定义1报酬与名字无关，只与参与人的贡献有关，k，g分别表示联盟中两个参与人，若k与g互换也不影响A时，fk(A)=fg(A)。

定义2收益属于参与人全部，∑k∈Ufk(A)=f(A,U)对所有U⊂S均成立，如果存在虚拟参与人，虚拟参与人的收益为0。

定义3可加性，若有两个工作A1与A2，则fk(A1,A2)=fk(A1)+f(A2)对所有k均成立。

对所有U⊂S，f(A,U)可以根据联盟收益模型求得，则fk(A)的唯一解为：

(8)

S为联盟U中参与人的个数，U-(k)表示联盟U中去掉成员k。f(U)-f(U-{k})表示k参与人带给联盟U的边际收益，不一定全部由k创造，但是它带来的。

2.3联盟稳定性判断

(1)个体理性

联盟的稳定需要确保联盟参与人都从联盟中获得收益，也就是政府给予企业的补贴必须要小于合作中政府成本的节约，企业获得补贴必须大于政企联合储备下企业投入资金的机会成本。c(xi)为政府的成本函数，对于政府来讲无论企业是否合作，政府都要完成应急物资储备任务，政府的机会成本c(xi)=0；如果采用政企联合储备方式，政府从联盟中获得收益f(xi)>0，即认为政府会加入联盟。企业从联盟中获得收益f(xj)；企业的机会成本为c(xj)，主要指企业参与合作联盟所动用资金的机会成本。如果满足(c(xj)

(9)

pj为企业的内部收益率。

(2)联盟理性

联盟稳定性还要满足联盟理性，即任何参与人退出联盟会导致联盟的收益减少，假设参与人k将退出联盟，因为(f(xk)+f({U}-xk))

f({U,xk})>(f(xk)+f(U))

(10)

3算例分析

3.1算例分析

表2　联盟收益

表2中，没有政府参与的联盟收益均为0，与实际情况相符。针对表2中收益为正的联盟，运用shapley值对收益进行分配，同时计算出联盟参与人的机会成本，如表3所示。

表3　收益分配结果及机会成本

(1)分析表3的结果，从个体理性角度出发，所有联盟中参与人获得的收益大于其参与联盟的机会成本，联盟满足个体理性要求；从集体理性出发，联盟4、7的总收益最大且相同，在联盟7中政府获得的收益更大些。但是仔细对比分析联盟4和7，我们发现联盟7中多了第3个企业的加入，该企业在联盟中分配了收益，但是该企业的机会成本为0，即出现了交叉补贴情况，这对于其它参与人是不公平的，因此联盟7是不稳定的。政企联合博弈的最终结果为形成合作联盟4。

(2)从政企联盟收益分配结果看出，政府总是拿大头；因为政府起到“地主”角色，没有政府的参与政企联合没有实际意义；但是企业不完全等同“农民”，企业有自己的选择权，只有联盟获得的收益大于其机会成本时，才可能参与联盟。

3.2参数的敏感性分析

(1)企业内部收益率敏感性分析

本文算例分析中假设三个企业的内部收益率为(10%，12%，10%)，现增加各个企业的内部收益率，新的内部收益率为(12%，15%，15%)，其它数据不变，计算结果如表4所示。

表4　收益分配结果及机会成本(增加企业内部收益率)

分析表4的结果，从个体理性角度出发，联盟3、5、7中联盟参与人获得的收益小于其参与联盟的机会成本情况，予以去除；从集体理性出发，联盟4获得的收益最大，政企联合博弈的最终结果为形成合作联盟4。增加企业的机会成本(本文表现为企业内部收益率增加)，政企联合实物储备对企业的诱惑力会相应下降，逐渐出现企业不愿意参与联盟情况，这对政府是不利的，此时政府可以拿出自身部分收益补贴企业，提高企业加入联盟的积极性。

(2)缺货成本敏感性分析

本文算例分析中应急物资的每天缺货成本为4元，政府自身储备应急物资的每天成本为3元，企业储备应急物资的每天成本分别为2.1元、2.1元、2.3元。假设应急物资每天缺货成本为2.5元，其它数据不变，计算结果如表5所示。

表5　收益分配结果及机会成本(缺货成本为2.5元)

对比分析表3和表5，联盟8的出现表示政府可能选择缺货策略，因为缺货成本低于政府自身储备的成本，政府反而会获得一个额外的收益；由于缺货成本小于政府自身成本，当联盟的储备能力小于应急物资总需求量时，政府依然选择部分缺货，联盟1、2、3出现缺货；表5中各个联盟的总收益均大于或等于表4中对应联盟收益，因为政府缺货获得的收益大于自己储备应急物资的收益。

分析表5结果，缺货成本降低导致所有可能联盟中企业获得的收益都小于企业自身的机会成本，企业不愿意加入政企联盟，政企联合博弈的最终结果为形成合作联盟8，政府选择缺货。本文继续降低应急物资的缺货成本至2元，其它数据不变，计算结果如表6所示。

表6　收益分配结果及机会成本(缺货成本为2元)

表6的结果可以看出，缺货成本低于企业储备成本时，联盟显得无意义，政府会选择缺货。

4结论与展望

本文研究应急物资政企联合实物储备合作机理，分析了联盟参与人之间的博弈关系，建立了联盟收益模型，运用shapley值解决合作联盟收益分配问题，最后分析了联盟的稳定性。算例分析可知：(1)在政企联合实物储备博弈中政府起到“地主”的角色，没有政府的参与政企联合没有实际意义，政府收益的大小取决于联盟的组成；企业不完全是“农民”角色，企业有自己的选择权，只有从联盟获得的收益大于其机会成本时，才愿意参与联盟；(2)增加企业的机会成本，政企联合实物储备对企业的诱惑力会相应下降，企业不愿意参与联盟，这对政府不利，此时政府可以拿出自身部分收益补贴企业，提高企业加入联盟的积极性；(3)当缺货成本低于政府储备成本时，政府会考虑与企业联合储备或者缺货，当缺货成本低于企业储备成本时，政府选择缺货。本文研究内容有限，对于非完全竞争市场，企业之间可能会形成小联盟与政府进行博弈，可作为接下来研究的内容。

参考文献：

[1]Chen T, Huang J. Exploratory research on the system of china relief reserve[J]. Systems Engineering Procedia, 2012, 5: 99-106.

[2]张自立,李向阳,王桂森.基于生产能力储备的应急物资协议企业选择研究[J].运筹与管理,2009,18(1):146-150.

[3]张自立.面向非常规突发事件的生产能力储备模型研究[D].哈尔滨工业大学,2010.

[4]丁斌,桂斌.基于合作博弈的预付条件下应急物资库存策略[J].运筹与管理,2011,20(3):60-65.

[5]王军.水上救援资源优化配置问题研究[D].大连海事大学,2011.

[6]丁斌,雷秀,孙连禄.应急物资储备方式选择与成本分摊问题[J].北京理工大学学报(社会科学版),2011,13(6):73-78.

[7]Shapley L S. A value for n-persons games[J]. Annals of Mathematies Studies, 1953, 28: 307-318.

[8]Owen G. Values of games with a priori unions[C]//Proceedings of Mathematical Economic and Game Theory. Berlin: Springer-Verlag, 1977: 76-88.

[9]Straffin P D, Heaney J P. Game theory and the tennessee valley authority[J]. International Journal of Game Theory. 1981, 1: 35-43.

[10]董保民，王运通，郭桂霞.合作博弈论[M].中国市场出版社,2008.