小波-SG-EEMD混合算法及混沌去噪应用研究
2016-01-15位秀雷,林瑞霖,刘树勇等
第一作者位秀雷男,博士生,1988年10月生
通信作者刘树勇男,博士,副教授,1975年11月生
小波-SG-EEMD混合算法及混沌去噪应用研究
位秀雷,林瑞霖,刘树勇,王强
(海军工程大学动力工程学院,武汉430033)
摘要:混沌信号和噪声频谱部分甚至全部重叠,单一的去噪方法无法有效地从强干扰中提取有用信号,为此,提出了小波-SG-EEMD混合去噪算法。该算法将小波-SG作为EEMD的预滤波单元,有效降低白噪声和局部强干扰的影响,并结合EEMD抑制模式混叠的特性,可以有效地将混沌信号从复杂干扰中提取出来。利用Lorenz时间序列详述了混合滤波算法的实施过程,并将该方法用于两自由度混沌振动信号中。结果表明该方法切实可行,具有非常好的应用价值。
关键词:混沌信号;小波变换;SG算法;EEMD
基金项目:国家自然科学基金(51179197);海洋工程国家重点实验室(上海交通大学)开放课题(1009)
收稿日期:2014-05-19修改稿收到日期:2014-08-29
中图分类号:O322
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.17.017
Abstract:Since some or all of spectral bands of chaotic signals and those of noise overlap, chaotic signals cannot be extracted effectively from strong disturbances with a single denoising method. Here, the hybrid wavelet-SG-EEMD algorithm was proposed. With the proposed algorithm, the wavelet-Savitzky-Golay(wavelet-SG) algorithm was taken as the pre-filter element of the ensemble empirical mode decomposition(EEMD) in order to reduce the effects of random white noise and local strong disturbances, and then the hydrid algorithm was combined with the characteristics restraining mode mixing of EEMD to extract the chaotic signals from complex and strong disturbances effectively. The implementation of the hybrid filtering algorithm was evaluate with Lorenz time series. Finally, the method was applied in 2-DOF chaotic vibration signals, and the results showed that the strong noise can be filtered normally.
Hybrid wavelet-SG-EEMD algorithm and its application in chaotic de-noising
WEIXiu-lei,LINRui-lin,LIUShu-yong,WANGQiang(College of Power Engineering,Naval University of Engineering, Wuhan 430033, China)
Key words:chaotic signal; wavelet transformation; SG algorithm; EEMD
近年来,由确定系统产生的混沌现象在很多学科中得到了广泛应用[1]。但是,由于受到测量工具以及外界环境等影响,实际采集到的混沌信号不可避免地混有噪声,掩盖了混沌信号的真实动力学行为[2]。混沌信号具有功率谱宽带性和似噪声性,其频带与叠加的其他信号的频带往往全部或部分重叠,尤其对于较低信噪比的混沌信号,现有的单一方法难以实现有效滤波[3]。
Huang等[4]提出了处理非线性非平稳信号的新方法——经验模态分解(Empirical Mode Decomposition, EMD),与小波变换方法相比,EMD无需信号的先验知识,其分解完全依赖信号本身,数据分解真实可靠。冷建成等[5]将EMD应用于混沌信号去噪,展现了EMD简单、实效、鲁棒性好的优点。但是,Boudraa等[6]比较了EMD和小波阈值去噪方法,发现后者去噪效果要优于EMD,特别在受到脉冲强干扰的情况下,EMD方法分解出来的本征模态分量(Intrinsic Mode Function,IMF)会发生畸变,导致信号失真[7],且EMD本身存在一些不足,如模式混叠、端点效应、停止条件等[8]。为了抑制模式混叠,Wu等[9]提出了集合经验模态分解方法(Ensemble Empirical Mode Decomposition,EEMD),有效地克服了这一缺陷,随后,很多学者在此基础上进行了改进,并应用于振动信号的去噪处理,取得了较好的效果[8,10]。实测的混沌振动信号往往存在较强的随机噪声和脉冲干扰,尤其低信噪比条件下,信号几乎被噪声淹没,以上单一的方法很难有效地将混沌信号从强干扰中提取出来,从而严重影响了混沌信号进一步的识别或预测等处理。为此,本文根据混沌信号本身的特点,结合小波和Savitzky-Golay(SG)滤波方法,在保留混沌信号特征的前提下最大限度地抑制白噪声和局部强干扰的影响,再将预处理后的信号作为EEMD的输入信号,以减少其不必要的分解层数,提高实效性,形成小波-SG-EEMD的混合去噪模型,并将这一模型应用于两自由度混沌振动信号中,结果表明该方法简单可行,切实有效,具有非常好的应用价值。
1EEMD基本原理
EEMD的基本思想是利用白噪声频谱的均匀分布来使不同尺度的信号自动分布到合适的参考尺度上。同时,利用白噪声的零均值特性,经过多次平均使噪声相互抵消,从而抑制甚至完全消除噪声的影响。其步骤如下:
(1)在原始信号x(t)中叠加均值为0,幅值和标准差为常数的高斯白噪声ni(t),i=1~M,叠加次数为M(M>1),即:
xi(t)=x(t)+ni(t)
(1)
(2)对xi(t)进行EMD分解,得到N个IMF记为aij(t),j=1~N,余项表示为ri(t)。
(3)由于不相关随机序列的统计均值为0,所以将以上步骤所得的IMF进行平均运算,即可消除多次叠加高斯白噪声对真实IMF的影响,平均后得到的IMF为:
(2)
aj(t)表示对原始信号进行EEMD分解后所得的第j个IMF。
2小波-SG模型建立
小波变换是近年来新发展起来的时频表征工具,对白噪声具有很强的抑制能力[11],但是抑制局部脉冲干扰的能力较弱,这是由于脉冲干扰幅值较大,波宽较窄时,经小波分解后其小波系数大于设定的阈值,致使经过多尺度分解滤波,脉冲干扰仍不能得到有效抑制[12]。相反,Savitzky-Golay平滑滤波算法是一种移动窗口的加权平均算法,在平滑脉冲干扰的同时,还可以保留信号的细节特征[13]。因此,建立小波-SG模型对信号进行预处理,可以同时有效地减少随机白噪声和局部脉冲干扰的影响。
小波-SG滤波算法具体步骤如下:
(1)对含噪信号进行J尺度小波分解,得到相应的小波分解系数:
(3)
式中:cj,k和dj,k分别表示近似系数和细节系数,h和g表示滤波器的脉冲响应,j为响应的分解尺度。
(2)为了抑制脉冲干扰,对近似系数cj,k和细节系数dj,k均按式(4)做SG平滑处理。以第一层小波分解后的近似系数c1,k为例,设ci是其中的一个小波系数,在ci附近以nl+nr+1个点在最小二乘意义下拟合一个M次多项式pi(c),多项式pi(c)在ci的值,即光滑数值gi表示为:
(4)
nl为ci左边点的个数,nr为ci右边点的个数,bp为多项式的系数。设实测数据为yi,为了使pi(c)拟合测试数据,必须定义系数bp,使得式(5)达到最优。
(5)
(3)保持平滑后的近似小波系数不变,根据式(6)对平滑后的细节小波系数进行阈值量化处理。
(6)

(4)将经过步骤1~3处理过的近似系数和细节系数按照式(7)进行重构。
(7)
3小波-SG-EEMD混合去噪分析
基于以上分析,小波-SG-EEMD混合去噪的基本流程可用图1表示。被分析信号x(t)通过小波-SG预处理,将处理后的信号进行EEMD分解,最后重构IMF分量达到去噪目的。

图1 小波-SG-EEMD混合去噪框架 Fig.1 The denoising flow chart of hybrid Wavelet-SG-EEMD
下面以加入白噪声和脉冲干扰的Lorenz时间序列为例,对本文方法进行分析。
3.1EEMD抗混分析
文献[4]指出,引起模式混叠的主要原因是受外部异常事件的影响,如间断信号,脉冲干扰和白噪声等。为了验证受干扰条件下混沌信号EEMD分解的抗混能力,本文以叠加5 dB的Lorenz时间序列和Gauspuls脉冲分量组成的信号进行仿真分析,其中Gauspuls脉冲干扰的中心频率fc=1 000 Hz,相对带宽bw=0.5。
图2(a)为仿真信号的EMD分解结果,包括三个IMF分量(a1~a3)和一个余项res。其中,a1完全失真,失去了物理意义,a2在干扰附近(箭头所标位置)是干扰和Lorenz序列的模式混叠,分布有两者的特征时间尺度。图2(b)为仿真信号的EEMD分解结果,加入0.4倍信号标准偏差的高斯白噪声,加入次数M=100,包括八个IMF分量和一个余项res,为了方便和EMD的分解结果作比较,将第三至第七个IMF分量叠加,结果如a3所示。可以看出,第二个IMF分量a2并未出现明显的模式混叠,其在时间尺度上介于a1和a3之间,是由于干扰和Lorenz序列调制所致。

图2 仿真信号的EMD和EEMD结果 Fig.2 EMD and EEMD results of simulation signal
表1给出了EMD和EEMD去噪所耗时间以及去噪后信号的信噪比(SNR)和均方误差(MSE),可以看出,EEMD的去噪效果要优于EMD,但是耗时过多,时效性差,这主要是由于高斯白噪声的叠加以及过多的分解层数所致。

表1 两种分解方法比较
3.2混合去噪的必要性分析
对于信噪比较高且受单一干扰影响的混沌含噪信号,常用的去噪方法,如小波分析、EMD、局部投影等都能取得较好的信噪分离效果。若是受到复杂强干扰的混沌信号,单一的信噪分离方法效果将会如何。以信噪比为-5 dB的Lorenz时间序列为例,并叠加Gauspuls脉冲干扰对本文所提方法的必要性进行分析,干净的Lorenz时间序列和叠加干扰的含噪序列见图3。
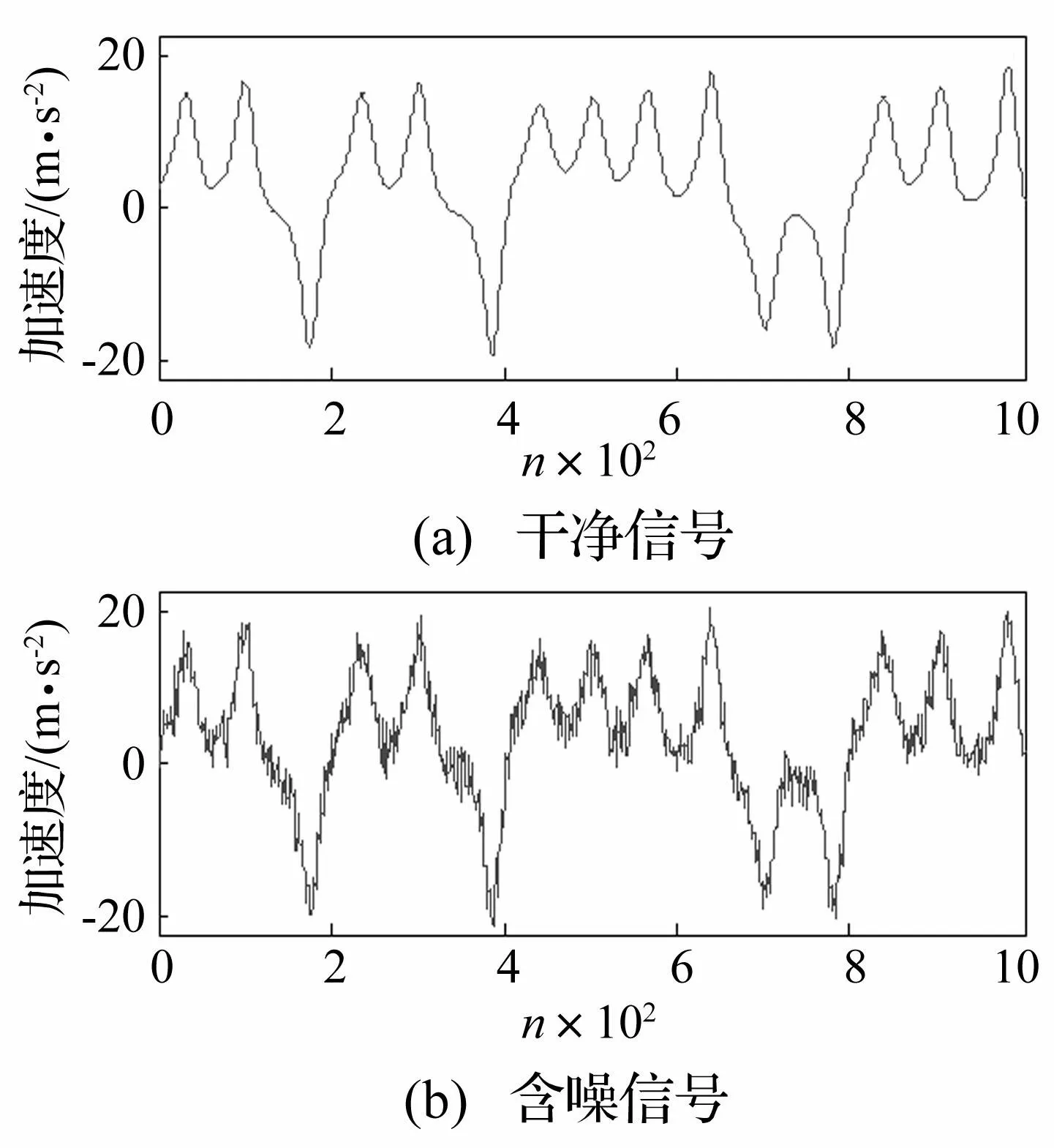
图3 Lorenz时间序列 Fig.3 Lorenz time series
首先,利用小波分析和对信号进行去噪处理。小波基选用正交性和紧支撑性较好的‘db4’小波,分解层数设为3。阈值函数和阈值分别选用软阈值函数和固定阈值,去噪结果见图4(a),可以看出,脉冲干扰和白噪声都未得到很好的抑制。图4(b)为小波-SG的去噪结果,SG算法的拟合阶数取3,数据窗口为15,脉冲干扰虽然得到了有效地抑制,但是信号局部存在明显畸变。
图5(a)为含噪信号EEMD的分解过程。得到八个IMF分量(a1~a8)和一个余项res。舍去a1,将a2和a3进行软阈值处理,并和低频部分a4~a8、余项res叠加重构便得到去噪结果见图5(b),部分脉冲干扰并未去除,且由噪声引起的信号畸变比较突出。

图4 两种方法的去噪结果 Fig.4 The denoising results of the two methods

图5 仿真信号的EEMD处理结果 Fig.5 The EEMD results of simulation signal
图6是本文方法的去噪结果,只需分解7个IMF分量便可得到平滑的Lorenz序列,减少了过多分解层累积的端点误差,且分解得到的IMF分量未发生明显畸变。这是由于小波-SG作为EEMD的预滤波单元,消除了大部分白噪声和脉冲干扰,减少了EEMD分解过程中不必要的高频噪声分解层,降低了过多分解层积累的端点误差,提高了分解的准确性。表2给出了以上方法的运行时间,本文方法耗时要小于EEMD,大大提高了EEMD的时效性。
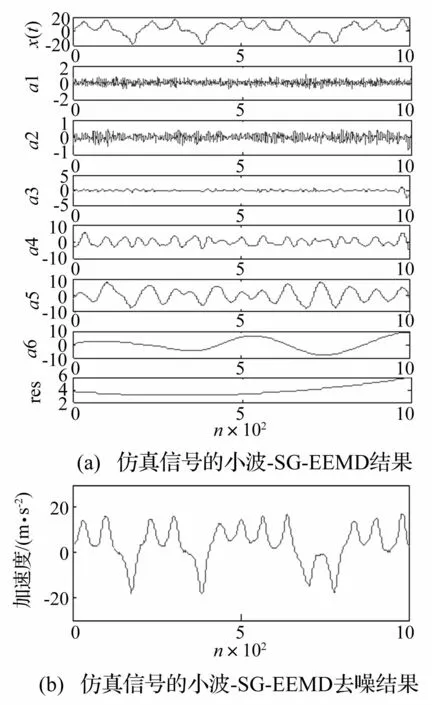
图6 仿真信号的小波-SG-EEMD处理结果 Fig.6 The denoising results of simulation signal based on Wavelet-SG-EEMD

小波分析小波-SGEEMD本文方法耗时/s0.04490.139911.46928.6176
4两自由度非线性振动信号处理
为了进一步验证本文所提方法对于混沌信号的去噪效果,以两自由度非线性振动信号为对象,模拟混沌振动信号,其动力学系统模型见图7,根据牛顿定理,系统的运动微分方程为:
(x1-x2)3=fcos(ωt)+G

图7 两自由度振动系统 Fig.7 Two-degree-of-freedom vibration isolation model
当参数ξ1=0.02,ξ2=0.2,K=100,f=8.8,G=96时,系统处于混沌状态[16]。x1-x3的相图见图8(a)。对其叠加-5 dB的高斯白噪声和脉冲干扰,分别利用小波-SG、EEMD和本文方法对其进行去噪处理,图8(b)、(c)和(d)分别对应其去噪效果图,通过比较可以看出,小波-SG和EEMD去噪效果不是很明显,信号曲线较为粗糙,而本文所提方法对于混沌振动信号去噪效果优于以上两种方法。为了定性比较以上三种方法的去噪效果,表3分别列出了去噪后信号的信噪比和均方误差,可以看出,本文方法的降噪指标SNR相对较高,而MSE相对较低,可见,利用小波-SG作为EEMD的预处理单元对信号进行降噪处理能达到较好的效果,切实可行,具有非常好的应用价值。

图8 三种方法去噪结果比较 Fig.8The denoising results of three methods above

小波-SGEEMD本文方法SNR/dB14.295313.873215.3742MSE1.35271.42531.2742
5结论
本文结合小波分析抑制白噪声和SG平滑脉冲干扰的功能,将小波-SG作为EEMD分解的预滤波单元,减少了白噪声和脉冲干扰的影响,避免了EEMD分解过程中不必要的高频噪声分解层以及过多分解层累积的端点误差,克服了IMF分量选取的问题。仿真实验和两自由度混沌振动信号去噪结果表明,小波-SG-EEMD可以有效地从复杂强干扰影响下提取混沌信号,保证了混沌识别的准确性,具有非常好的应用价值。
参考文献
[1]Alexander L F,Robin J E. Control of chaos: Methods and applications in engineering[J] . Annual Reviews in Control,2005,29( 1):33-56.
[2]Kostelich E J,Schreiber T. Noise reduction in chaotic time series: A survey of common methods[J]. Physical Review E (S1063-651X),1993,48(3):1752-1763.
[3]Elshorbagy A,Simonovic S P,Panu U S. Noise reduction in chaotic hydrologic time series: facts and doubts[ J]. Journal of Hydrology,2002,256(3-4):147-165.
[4]Huang N E,Shen Z,Long S R,et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Science,1998,454:903-995.
[5]冷建成,刘树林. 基于EMD的混沌信号去噪研究[J]. 振动与冲击,2006,25(增刊):326-328.
LENG Jian-cheng,LIU Shu-lin. Noise reduction of chaotic signal based on EMD method[J]. Journal of Vibration and Shock,2006,25(Sup):326-328.
[6]Boudraa A O,Cexue J C. De-noising via empirical mode decomposition[C]//Proceedings of the IEEE International Symposium on Control Communications and Signal Processing,Marrakech,Morocco:IEEE,2006:4-8.
[7]柏林,刘小峰,秦树人. 小波-形态-EMD综合分析法及其应用[J].振动与冲击,2008,27(5):1-4.
BO Lin,LIU Xiao-feng,QIN Shu-ren. Hybrid wavelet-morphology-EMD analysis and its application[J]. Journal of Vibration and Shock,2008,27(5):1-4.
[8]陈仁祥,汤宝平,马靖华. 基于EEMD的振动信号自适应降噪方法[J]. 振动与冲击,2012,31(15):82-86.
CHEN Ren-xiang,TANG Bao-ping,MA Jing-hua. Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal[J]. Journal of Vibration and Shock,2012,31(15):82-86.
[9]Wu Z,Huang N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proc. R. London A,2004,460:1597-1611.
[10]张袁元,李舜酩,胡伊贤,等. LMS方法的改进及联合EEMD在振动信号去噪中的应用[J]. 振动与冲击,2013,32(20):61-66.
ZHANG Yuan-yuan,LI Shun-ming,HU Yi-xian,et al. Improvement of LMS method and its application combined with EEMD in vehicle vibration signal denoising[J]. Journal of Vibration and Shock,2013,32(20):61-66.
[11]Chiementin X,Kilundu B,Rasolofondraibe L,et al. Performance of wavelet denoising in vibration analysis:highlighting[J]. Journal of Vibration and Control,2012,18(6):850-858.
[12]滕军,朱焰煌,周峰,等. 自适应分解层数的小波域中值滤波振动信号降噪法[J]. 振动与冲击,2009,28(2):58-62.
TENG Jun,ZHU Yan-huang,ZHOU Feng,et al. Vibration signal denoising method based on median filter in wavelet domain with self-adaptive level decomposition[J]. Journal of Vibration and Shock,2009,28(2):58-62.
[13]李亢,杨绍清. 基于Savitzky-Golay算法的图像平滑去噪[J]. 数据采集与处理,2010,25(增刊):72-74.
LI Kang,YANG Shao-qin. Image smooth denoising based on Savitaky-Golay algorithm[J]. Journal of Data Acquisition & Processing,2010,25(Sup):72-74.
[14]Roggen Y. Wavelet denoising using principal component analysis[J]. Expert Systems with Applications,2011,81(2):1073-1076.
[15]刘树勇,位秀雷,许师凯,等. 非线性混沌振动响应的试验分析[J]. 噪声与振动控制,2014,34(2):5-7.
LIU Shu-yong,WEI Xiu-lei,XU Shi-kai,et al. Experimental research of nonlinear chaotic vibration responses[J]. Noise and Vibration Control,2014,34(2):5-7.
[16]楼京俊. 基于混沌理论的线谱控制技术研究[D]. 武汉:海军工程大学,2006.


