端部起爆下空腔装药对离散杆驱动特性的影响研究
2016-01-15魏继锋,魏锦
第一作者魏继锋,男,博士,副教授,1977年生
端部起爆下空腔装药对离散杆驱动特性的影响研究
魏继锋,魏锦
(北京理工大学爆炸科学与技术国家重点实验室,北京100081)
摘要:研究端部起爆下不同空腔直径装药的爆轰输出特性及对杆条驱动特性的影响。采用非线性动力学软件LS-DYNA,运用流固耦合算法,对不同空腔直径装药下离散杆的爆轰驱动过程进行数值模拟,分析空腔直径大小对爆轰产物压力分布、离散杆速度与微元速度分布以及离散杆变形的影响。仿真结果表明,随着空腔直径的增大,空腔内稀疏效应逐渐增强,使得爆轰输出压力沿轴向趋同;杆条速度随空腔直径的增大非线性减小,杆条微元速度梯度逐渐减小;空腔直径越大,杆条平直度越好,而杆条平直度与杆条速度呈反向变化规律,因此离散杆的最优作用效果要综合权衡飞散速度与平直度。
关键词:爆炸力学;离散杆;空腔装药;驱动特性
基金项目:部级科研基金(04010103)
收稿日期:2014-06-09修改稿收到日期:2014-10-17
中图分类号:TJ410.2
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.17.010
Abstract:By changing hollow diameter of cylindrical charge with one end initiation, its detonation output characteristics and influences on driving characteristics of a discrete rod were studied. Numerical simulations of discrete rods’ detonation driving processes were performed with the nonlinear dynamic analysis program LS-DYNA and the fluid-solid interaction method. The influences of different hollow diameters on pressure distribution of detonation products, velocity, micro-unit velocity distribution and effective length of discrete rod were analyzed. The simulation results showed that with increase in hollow diameter, gradually enhanced sparse effects make the pressure along the axial direction tend to the same; the resultant velocity of the discrete rod decreases nonlinearly with increase in hollow diameter and the micro-unit velocity gradient also decreases; the larger the hollow diameter, the better the flatness of the rod, while the flatness has a reverse variation to the velocity of the rod; so the optimal effect of the discrete rod should consider the balance between its velocity and flatness.
Effects of hollow cylindrical charge with one end initiation on driving characteristics of a discrete rod
WEIJi-feng,WEIJin(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China)
Key words:explosion mechanics; discrete rod; hollow cylindrical charge; driving characteristics
离散杆是一种常见的毁伤元形式,除了质量及加载速度外,完整性与平直度也是衡量其是否具有良好杀伤效果的重要指标。杆条受驱运动是典型的爆轰加载驱动问题,受力不均会使杆条内应力超过材料的屈服极限,产生弯曲变形,严重时发生断裂,而爆轰波结构则是杆条获得理想驱动的内因,据此开展深入研究具有重要的学术价值和研究意义。
为了调节爆轰波结构、改善离散杆的驱动特性,开展了隔板、空腔、起爆方式等调整爆轰波形结构的研究工作。姚翠友等[1]研究了直线形、折线形和抛物线形三种隔板,计算表明折线形隔板对防止杆条破碎方面较优。郭华等[2]对一定空腔装药结构的爆轰驱动过程进行了三维数值模拟,得到了破片速度的变化规律。Zhang等[3-4]基于经典Gurney模型,推导出无限长空腔装药的破片初速计算方法。梁争峰等[5]采用大直径空腔、两端冗余装药来调节爆轰波结构,获得了等强度爆轰驱动效果。Wei等[6]分析了中心起爆和偏心起爆对杆条运动规律的影响。
以往研究并没有细致考虑空腔对爆轰加载特性的影响,也没有深入探讨空腔和离散杆飞行姿态间的关系。本文进行了端部起爆方式下空腔装药对离散杆驱动加载问题的数值模拟,分析了空腔直径对爆轰输出特性与杆条运动特性的影响,得到了杆条整体速度、微元速度、杆条变形随装药空腔直径的变化规律。
1物理模型
模型直径127mm,长140mm。端盖、底盖分别与壳体相连,端盖与底盖均厚5mm,壳体厚3mm;衬筒与壳体同轴,空腔装药置于衬筒与壳体之间,装药空腔直径d分别为0mm、20mm、40mm、60mm、80mm、100mm。杆条Ф4×110mm,96根均匀围绕在壳体的整个圆周上,见图1。杆条材料为钢,壳体、衬筒、端盖和底盖材料均为铝,空腔装药为B炸药。
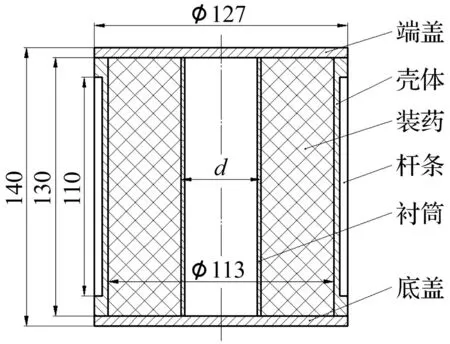
图1 结构及尺寸图 Fig.1 Structure anddimension of model
2有限元计算模型
2.1算法与模型建立
装药爆轰驱动是一个典型的流固耦合问题,宜采用ALE算法进行研究。该算法一个单元可以包含多种介质,可完成物质在空间网格内的运输,能够克服单元严重畸变引起的数值计算困难,并能够实现流体与固体耦合的动态分析,从而能够准确描述空腔装药的爆轰过程以及结构的瞬态响应过程。
空气和装药被剖分成Euler单元,衬筒、壳体、端盖、底盖和杆条为Lagrange单元。按照前述物理模型的结构尺寸建立有限元模型,见图2。仿真模型采用的基本单位制为:cm-g-μs。

图2 有限元模型 Fig.2 The finite element model
2.2材料模型与状态方程
计算过程中涉及到的材料包括B炸药、铝和钢。空腔装药采用HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程。JWL状态方程能精确地描述在爆轰驱动过程中爆轰产物的压力、体积、能量特性[7],表达式为:
(1)
式中:A、B、R1、R2、ω均为炸药JWL方程的系数。空腔装药基本材料参数见表1。ρe为炸药密度,De为爆速,PCJ为C-J压力。

表1 B炸药基本材料参数
铝材料和钢材料均采用弹塑性动力学硬化材料模型,具体参数见表2。其中ρ为材料密度,E为杨氏模量,ν为泊松比,σ为屈服应力,η为剪切模量,β为硬化参数。空气采用MAT_NULL材料模型和EOS_LINEAR_POLYNOMIAL状态方程。
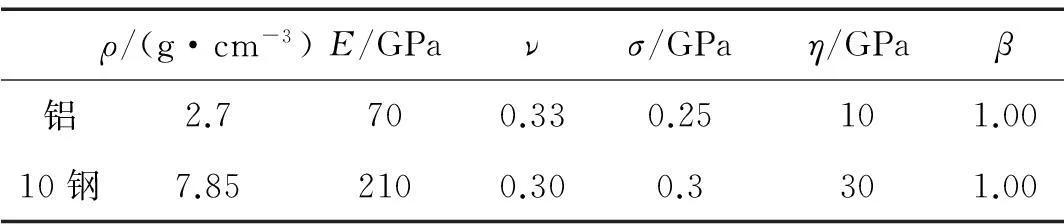
表2 铝和钢材料参数
3仿真结果与分析
3.1空腔直径对爆轰输出特性的影响
装药起爆以后,爆轰波以近似滑移爆轰的形式自上而下传播。爆轰产物作用于壳体内壁面,使得圆柱壳体在径向压力作用下发生拉伸、弯曲、剪切变形而膨胀、破裂形成破片[8-9]。同时壳体在爆轰产物膨胀作用下推动杆条向外加速运动。对比不同时刻,不同空腔直径装药外侧沿轴向由起爆端(x=0mm)至非起爆端(x=130mm)爆轰产物的压力分布,见图3和图4。
当t=20μs时,爆轰波传播刚刚结束,此时不同空腔直径下的压力变化趋势基本相同。随着空腔直径的增大,沿径向方向装药厚度减小,使得整体的压力值减小。当装药不存在空腔时,压力峰值为4.5GPa,而当空腔直径d=80mm时,压力峰值降低至1.8GPa。

图3 20μs时装药外侧沿轴向的压力分布 Fig.3 Pressure distribution of the charge along the axial direction at 20μs
空腔直径的变化影响了爆轰产物的继续膨胀,当t=30μs时,装药外侧沿轴向由起爆端至非起爆端的压力分布有了不同的变化。当空腔直径d=20mm时,从起爆端至x=110mm处压力均大于无空腔时的压力,且二者的最大压力均出现在距起爆端0.7倍的装药长度处,分别为0.91GPa和0.74GPa。随着空腔直径的继续增大,压力峰值出现的位置产生了不同的变化。当空腔直径为80mm和100mm时,压力沿轴向基本相同,均保持在一个较低的水平。
不同时刻下,当空腔直径在一定范围内变化时,压力总是先增大后减小,这是由于装药两端稀疏效应的影响导致压力减小,且稀疏效应对起爆端的影响大于非起爆端,同时沿装药径向方向也存在稀疏效应,但此时对压力的影响并不明显。当空腔直径逐渐增大,如空腔直径为80mm和100mm时,装药空腔体积增大,径向稀疏效应的影响趋于明显,使得压力沿轴向的变化并不显著。由装药空腔直径变化导致装药量的改变主要影响了整体压力的大小,而其带来的空腔体积的变化则主要影响了压力沿轴向分布的变化规律。
3.2空腔直径对杆条速度的影响
在杆条飞散过程中,不同空腔直径下杆条速度随时间的变化规律见图5。当装药起爆以后,受爆轰产物膨胀作用杆条速度迅速增大;当t=20μs时,壳体开始破裂,杆条加速度逐渐减小,速度缓慢增加;随着爆轰产物对杆条作用的不断减小,t=50μs以后,杆条保持恒定速度向外飞散。


图4 t=30μs时装药外侧沿轴向的压力分布Fig.4Pressuredistributionofthechargealongtheaxialdirectionat30μs图5 杆条速度随时间变化曲线Fig.5Velocity-timecurvesofdiscreterod图6 杆条速度随装药空腔直径的变化规律Fig.6Relationshipofdiscreterod’svelocityandhollowdiameter
在不考虑端部稀疏效应的条件下,E.F.Jones在Gurney公式的基础上,对战斗部中含有引信孔等空腔的情况对破片初速进行了修正[10]:
(1)
(2)

可以看出F与β都可表示为与装药空腔直径d相关的变量,此时杆条初速表达式为:
(3)
式中:D为装药外径,L为装药长度,M为壳体及杆条总质量。对于本文所研究模型,式(3)可化为:

(4)
将式(4)表示的杆条初速随空腔直径的变化趋势与仿真计算结果共示于图6。
计算结果均表明杆条初速与空腔直径存在非线性关系。式(4)虽未考虑端部稀疏效应的影响,但其对杆条初速的预估仍具有重要意义。仿真计算考虑了端部稀疏效应的影响,仿真值低于式(4)计算值;当空腔直径小于60mm时,相对误差在15%以内,此时稀疏效应的影响较小;当空腔直径为80mm和100mm时,相对误差值增大到19.0%和31.2%,说明稀疏效应的影响在增大。
3.3空腔直径对杆条微元速度分布的影响
从图5可以看出,t=50μs以后杆条不再受爆轰驱动作用,此时杆条速度已达到最大值。仿真计算中,将杆条离散化为若干微元,获得50μs时的杆条微元速度分布见图7。随着空腔直径的增大,杆条微元速度分布逐渐均匀;微元速度差的减小也将促使杆条变形程度减小。
对于两端自由的无空腔装药,考虑稀疏效应的影响,此时距引爆面x处的微元初速可用下式表示[11]:
(5)
(6)
式中:vx为坐标x处的壳体微元初速;imax为作用于壳体内表面的最大比冲量;ix为作用于坐标x处的壳体内表面的比冲量;α=x/L,i0=(8/27)ρLDe。
当壳体受爆轰产物作用推动杆条运动时,壳体各微元的速度也可看做杆条各微元的初速,由式(5)计算可知,当α=2/3,即距起爆端2/3的装药长度处,微元速度出现最大值。
将不同空腔结构下杆条微元速度的仿真结果与式(5)计算结果进行对比,见图8。

图8 t=50μs时杆条微元速度沿轴向分布 Fig.8 Micro-unit velocity distribution of discrete rod along the axial direction at 50μs
式(5)未考虑端部约束的影响,故杆条两端速度偏低。仿真计算中,无空腔装药的杆条微元速度变化规律与式(5)计算结果吻合(除端部外),速度最大值出现在装药轴向的2/3处。空腔直径越大,杆条各微元速度值越小,速度差也越小。表3示出了不同空腔直径下杆条微元的最大速度差,当装药无空腔时,杆条微元最大速度差达638m/s;当空腔直径为100mm时,最大速度差仅有42m/s。

表3 杆条微元速度对比
3.4空腔直径对杆条飞散姿态的影响
装药空腔通过影响爆轰输出特性最终影响杆条的飞散姿态。离散杆作为毁伤元时,完整性与平直度是其实现良好杀伤效果的重要指标。如果杆条变形过大,在目标投影面上的有效长度减少,将严重影响其毁伤效果。通常认为杆条有效长度达到其原长90%时,其能够实现杆条毁伤效果。

图9 150μs时不同空腔直径下杆条飞散形态 Fig.9 Shape of discrete rodwith different hollow diameter at 150μs
杆条在t=150μs时的飞散姿态见图9。从整体上来看,随着空腔直径的增大,杆条变形程度依次减小,平直度逐渐良好。当装药空腔直径在40mm范围内时,由图3和图4可知杆条在尾部(靠近非起爆端)受力较大,因此发生弯曲变形,且变形程度随着受力的减小而减小。当空腔直径d=60mm时,由图8可知,其杆条头部(靠近起爆端)速度较相邻微元有一个较大的提高,从而使得杆条在头部向内发生弯曲变形。随着空腔直径的继续增大,杆条沿轴向方向上的受力逐渐均匀,杆条各微元速度基本保持一致,杆条基本不变形。
计算不同空腔直径下,杆条在目标投影面上的长度,如表4。当装药无空腔时杆条变形严重,有效长度为原长的66.4%;当空腔为20mm时,空腔体积占空腔与装药总体积的3.1%,此时杆条仍具有较大变形;随着空腔直径的继续增大,杆条变形得到有效改善,有效长度逐渐增大,当空腔直径为80mm和100mm时,杆条有效长度已接近原长。
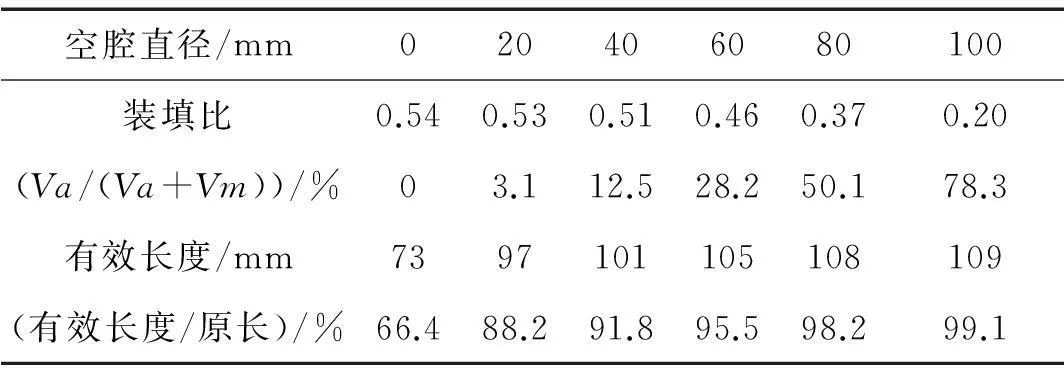
表4 杆条有效长度对比
4结论
通过研究装药空腔直径对爆轰输出特性和杆条飞散特性的影响,得出如下结论:
(1)装药空腔直径的增大,使得装药量逐渐减小,爆轰威力逐渐减弱;同时空腔体积的逐渐增大,空腔内稀疏效应逐渐增强,使得爆轰产物压力沿轴向趋同;
(2)杆条整体速度随空腔直径的增大呈非线性减小,空腔直径越大,杆条初速下降越快,杆条微元速度梯度随空腔直径的增大逐渐减小。当无空腔时,微元速度最大值与最小值相差638m/s,而当空腔直径为100mm时,仅为42m/s;
(3)离散杆的作用效果要综合考虑其飞散速度与平直度。无空腔装药的杆条速度高,杆条变形严重,有效长度仅为原长的66.6%;随着空腔直径的增大,杆条飞散速度下降,但杆条平直度增加,即杆条平直度与杆条速度呈反向变化规律。当杆条有效长度达到其原长的90%以上时,可认为其能够实现杆条毁伤效果,对于本文所研究结构,当空腔直径为40mm时,有效长度为原长的91.8%且速度达到1816m/s,具有最优的毁伤效果。
参考文献
[1]姚翠友, 娄春兰, 陈放, 等. 离散杆战斗部中隔板形状研究[J]. 北京理工大学学报, 1999, 19(增刊1): 61-64.
YAO Cui-you, LOU Chun-lan, CHEN Fang, et al. Study on theshape of linear in the discrete warhead[J]. Journal of Beijing Institute of Technology, 1999, 19(Sup1):61-64.
[2]郭华, 王树山, 马峰. 空腔装药爆轰驱动的三维数值模拟[J]. 弹箭与制导学报, 2004, 24(4): 305-307.
GUO Hua, WANG Shu-shan, MA Feng. Three-dimensions numerical simulation on the explosive driving of the hollow-charge[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004, 24(4): 305-307.
[3]Zhang Z W, Wang S S, Ma F. Gurney equation of the hollow-charge[J]. Theory and Practice of Energetic Materials, 2005, 6: 1117-1120.
[4]Wang S S, Li C Z. KE-Rod initial velocity of hollow cylindrical charge[J]. Defence Science Journal, 2011,61(1):25-29.
[5]梁争峰, 程淑杰, 郭双锋, 等. 爆轰场强对杆条姿态影响的数值模拟及试验[J]. 火炸药学报, 2011, 34(2): 52-55.
LIANG Zheng-feng, CHENG Shu-jie, GUO Shuang-feng, et al. Numericalsimulation and test on effects of explosive field intensity on rod attitude[J]. Chinese Journal of Explosives & Propellants, 2011, 34(2): 52-55.
[6]Wei J F, Li Y, Wang S S. Study on driving characteristics of discrete rod by different initiation styles[J]. Applied Mechanics and Materials, 2012(128-129): 318-322.
[7]毛亮, 姜春兰, 严翰新, 等. 可瞄准预制破片战斗部数值模拟与试验研究[J]. 振动与冲击, 2012, 31(13): 66-70.
MAO Liang, JIANG Chun-lan, YAN Han-xin, et al. Numerical simulation andexperiment on amiable warhead of premade fragment[J]. Journal of Vibration and Shock, 2012, 31(13): 66-70.
[8]孔祥韶, 吴卫国, 李晓彬, 等. 圆柱形战斗部破片速度及等效装药特性研究[J]. 振动与冲击, 2013, 32(9): 146-149.
KONG Xiang-shao, WU Wei-guo, LI Xiao-bin, et al. Fragment velocity and equivalent bare charge characteristic of cylindrical warhead[J]. Journal of Vibration and Shock, 2013, 32(9): 146-149.
[9]Sing M, Suneja H R, Bola M S, et al Dynamic tensile deformation and fracture of metal cylinders at high strain rates[J]. International Journal of Impact Engineering, 2002, 27: 939-954.
[10]张宝平, 张庆明, 黄风雷. 爆轰物理学[M]. 北京: 兵器工业出版社, 2006.
[11]张国伟. 终点效应及靶场试验[M]. 北京: 北京理工大学出版社, 2009.

