O型钢丝绳隔振器动态迟滞模型参数识别方法研究

第一作者王红霞女，博士生，讲师，1977年12月生

通信作者龚宪生男，博士生导师，1956年生

O型钢丝绳隔振器动态迟滞模型参数识别方法研究

王红霞1,2,3，龚宪生1,3，潘飞1,3，谯艳娟4

(1 .重庆大学机械传动国家重点实验室，重庆400044； 2.湖北汽车工业学院, 湖北十堰442002； 3.重庆大学机械工程学院，重庆400044；4.长安股份有限公司汽车工程研究院,重庆401120)

摘要：针对O型钢丝绳隔振器具有非线性弹性刚度、非对称迟滞动态特性,采用改进的归一化Bouc-Wen模型并基于该模型对钢丝绳隔振器动态特性参数识别方法进行研究。提出新的简单有效的两阶段识别方法进行参数辨识研究。通过数值仿真与周期性加载试验相结合方法对所提方法进行验证。结果表明，参数识别方法可准确有效识别出O型钢丝绳隔振器模型参数，且试验迟滞曲线与识别模型迟滞曲线吻合较好。

关键词：O型钢丝绳隔振器；迟滞；仿真；识别方法；改进的归一化Bouc-Wen模型

基金项目：国家自然科学基金(51175525)；973计划资助项目(2014CB049403)；湖北汽车工业学院博士基金(BK201406)

收稿日期：2014-04-21修改稿收到日期：2014-09-18

中图分类号:TU112

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.026

Abstract:A modified normalized Bouc-Wen model was adopted to describe the hysteretic behaviour of an O-type wire-cable vibration isolator which exhibits nonlinear elastic stiffness and asymmetric hysteresis dynamic behavior. The parametric identification of the O-type wire-cable vibration isolator was realized based on the modified normalized Bouc-Wen model. A new simple yet effective two-stage identification method was developed. Numerical simulations and periodic loading experiments were carried out to validate the proposed identification method. The results indicate that the proposed identification method is effective and accurate for identifying the model parameters of O-type wire-cable vibration isolator, and the experimental hysteresis loops are close to the identified hysteresis loops.

Parametric identification method for identifying dynamic hysteretic model parameters of O-type wire-cable vibration isolator

WANGHong-xia1,2,3,GONGXian-sheng1,3,PANFei1,3,QIAOYan-juan4(1. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044,China;2. Hubei Automotive Industries Institute, Shiyan, Hubei 442002,China; 3. College of Mechanical Engineering, Chongqing University, Chongqing 400044,China;4.Changan Automotive Engineering Institute, Chongqing 401120,China)

Key words:O-type wire-cable vibration isolator; hysteresis; simulation; identification method; modified normalized Bouc-Wen model

钢丝绳隔振器作为新一代干摩擦型阻尼迟滞隔振装置广泛用于诸多领域[1-4]。本文用多个彼此独立的钢丝绳圈作为隔振器弹性阻尼元件组成O型钢丝绳隔振器，见图1。该隔振器绳圈装夹更换方便、组装灵活、维修容易，可延长隔振器使用寿命。已有的对钢丝绳隔振器非线性迟滞系统参数识别方法的研究主要针对Bouc-Wen模型或其改进模型用实验数据进行参数识别，并取得较多成果。如时域最小二乘法[5-7]、频域最小二乘法[8-10]、扩展卡尔曼滤波算法[11-12]、顺序或自适应算法[13-14]等，均采用迭代算法寻找参数最优值，涉及初始参数选取，若果选取不当可能无法收敛、无法识别参数或得不到较优参数。Ikhouane等[15]针对迟滞系统提出归一化Bouc-Wen模型，并用极限环法[16]识别模型参数。该方法不涉及迭代算法，不存在收敛性问题。只要符合其适用范围，便能准确识别出相应参数。因此，本文提出新的简单有效的两阶段识别方法，基于试验数据对O型钢丝绳隔振器模型参数进行辨识研究。通过数值仿真及周期性加载试验相结合对该方法与另一模型及参数识别方法比较，验证该方法对O型钢丝绳隔振器模型参数识别的准确性、有效性。

图1　O型钢丝绳隔振器 Fig.1 O-type wire-cable vibration isolator

1O型钢丝绳隔振器迟滞模型

O型钢丝绳隔振器为典型的迟滞隔振装置。Bouc-Wen模型能有效描述迟滞系统动态特性[17]。归一化Bouc-Wen模型可表述为

f(t)=κxx(t)+κzz(t)

(1)

(2)

式中：f(t)为总恢复力；x(t)为输入激励位移；z(t)为迟滞因子；kxx(t)为弹性恢复力；kzz(t)为纯迟滞力；ρ，σ，n，kx，kz为归一化Bouc-Wen模型参数。

式(2)可写为

(3)

当z达到最大或最小值时，关系式成立

(4)

满足条件时z才能达到极值，即

(5)

由式(3)～式(5)求得z的极值为

zmin=-1,zmax=1

(6)

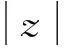
图2　归一化Bouc-Wen模型产生的纯迟滞力极限环 Fig.2 The pure hysteretic component limit cycle generated by the normalized Bouc-Wen model

O型钢丝绳隔振器在垂向承受正弦位移激励振幅A=7 mm、频率为5 Hz的拉压载荷试验迟滞环，见图3。由图3看出，试验迟滞环呈现非对称性。而归一化Bouc-Wen模型只能描述对称迟滞特性。

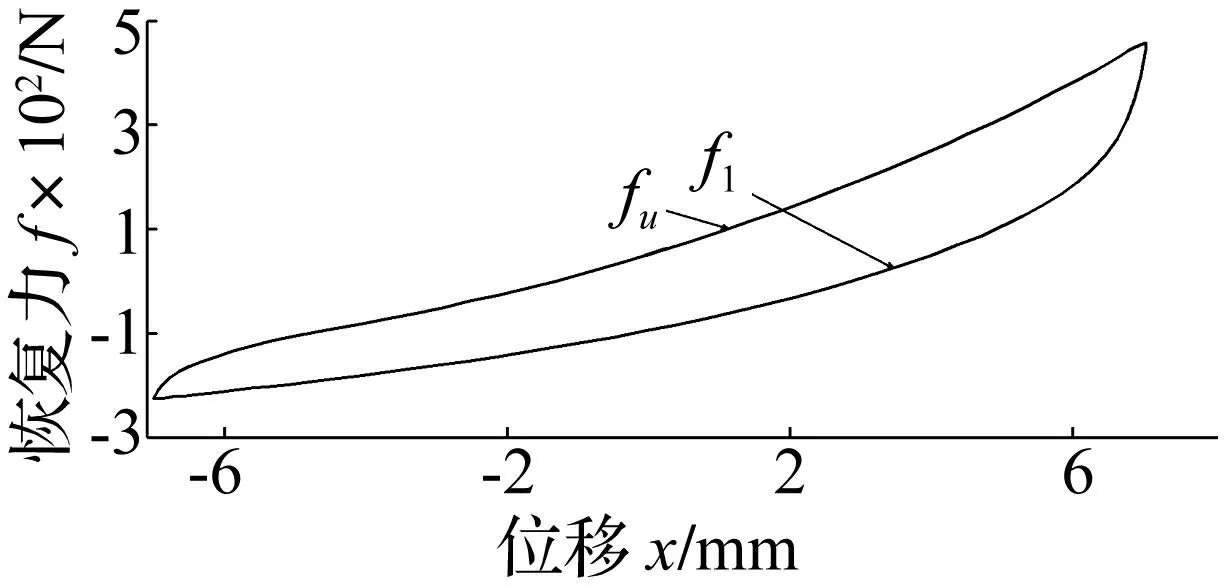
图3　O型钢丝绳隔振器动态响应试验迟滞环 Fig.3 The measured dynamic response of O-type wire-cable vibration isolator

为描述非对称迟滞环，基于归一化Bouc-Wen模型进行改进，该模型可表述为

f(t)=Fae+κzzFa

(7)

(8)

(9)

(10)

式中：Fae为非线性弹性恢复力；Fa为非线性放大因子；kaei，kaj分别为非线性弹性恢复力及非线性放大因子多项式系数；N，M分别为Fae，Fa的多项式阶数。

参数识别时此两多项式阶数及奇偶幂次确定可据试验数据及曲线拟合利用程序手动调整阶数N，M数值，以达到较好拟合效果。引入的两多项式阶数选取不同，模型拟合度亦不同。因此针对不同试验数据进行参数识别时多项式阶数可能不同。

2O型钢丝绳隔振器模型参数识别

2.1非迟滞参数的识别

由图2，激励位移x幅值较大、x取值远离最大或最小值即x在稳定段取值时，纯迟滞响应有界且对称。因此对幅值较大试验迟滞环(图3)，在稳定段式(7)中纯迟滞响应κzzFa有界，上界极值为kzFa。由于采集的试验数据是离散的，稳态响应稳定段恢复力在加、卸载时分别表示为

(11)

式中：fu，fl分别为稳定段加、卸载恢复力；下角标k为离散数据第k个点，k(1,2,…，K),K为离散数据长度。

识别Fa的相关参数，由式(11)知

(12)

此时kz取值尚未确定，非线性放大因子Fa无法求得。因此在稳定段假定某一点时

(13)

式中：x可取稳定段任意值。为便于计算，x取图3中一个周期内平均值x=0，即可求得κz，即

(14)

将式(14)代入式(12)得

(15)

式(9)可写为离散形式

(16)

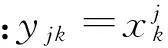
误差函数为

e(ka)=Fak-kayTak

(17)

对应的线性最小二乘式为

mine(ka)=‖e(ka)‖2

(18)

采用线性最小二乘法求解式(18)，从而求得放大系数矢量[ka1,ka2, …,kaM]。由式(8)求得非线性弹性恢复力Faek的表达式，用式(18)同样优化方法求得非线性刚度系数kae=[kae1,kae2, …,kaeN]。整个位移区间包括非稳定段据所求系数分别获得对应的拟合多项式。采用以上识别方法由试验迟滞环(图3)分解出非线性弹性恢复力Fae及其拟合见图4，非线性放大因子Fa及其拟合见图5。

图4　分解的多项式F ae及拟合的F ae Fig.4 The decomposed and predicted polynomials of F ae

图5　分解的多项式F a及拟合的F a Fig.5 The decomposed and predicted polynomials of F a

2.2识别纯迟滞响应中各参数

隔振器承载时纯迟滞响应产生的极限环可通过式(7)整体响应中提取。写成离散形式为

(19)

式中：θ=kzz为整体响应中提取的纯迟滞力曲线。用式(19)及已识别的非线性弹性恢复力Fae、Fa及参数κz，由(图3)动态响应试验迟滞环中提取的纯迟滞力曲线见图6。利用提取的纯迟滞力数据中隐含信息用极限环法结合式(10)识别出ρ,σ,n各模型参数。与第一阶段识别程序相似，参数识别过程不涉及迭代算法。

图6　O型钢丝绳隔振器纯迟滞力曲线 Fig.6 The pure hysteretic curve of O-type wire-cable vibration isolator

以试验数据为依据，据式(18)用线性最小二乘法先识别Fae与Fa相应参数及kz值；据第一阶段识别结果提取纯迟滞力极限环曲线，用极限环法识别出纯迟滞响应中各参数，获得改进的归一化Bouc-Wen模型所有参数值。

3数值仿真

为证实两阶段法的有效性，采用位移激励方式对O型钢丝绳隔振器动态特性进行数值仿真测试。针对钢丝绳隔振器具有垂向硬化重叠特性及非线性弹性刚度改进的Bouc-Wen模型及频域识别方法进行参数识别。仿真试验数据源自Ni’s模型，即

f(t)=F2a(t)[z(t)+F1a(t)]

(20)

F1a(t)=k1x(t)+k2sgn[x]x2(t)+k3x3(t)

(21)

F2a(t)=bcx(t)

(22)

(23)

式中：k1,k2,k3,b,c,α,γ,β,n为模型参数。

数值仿真中模拟的位移激励信号为

x=Asin(t)

(24)

式中：A为位移幅值，分别取3,4,5,6,7。

为使仿真响应数据更接近试验数据，加入适当噪声信号至输出信号。被噪声污染的输出恢复力fn(t)信号为

fn(t)=f(t)+εrif

(25)

式中：ε为噪声水平，指噪声与信号之比；f为f(t)幅值；ri为符合标准正态分布的随机变量。

数值仿真中取ε=0.025，据已有钢丝绳隔振器垂向动态特性模型参数识别结果k1=39.145，k2=1.360，k3=0.156，b=1.799，c=0.202，α=147.761，γ=-15.512，β=44.726，n=0.434，所得仿真试验数据fn(t)见图7。仿真流程见图8。

图7　一个周期不同幅值仿真输出响应数据 Fig.7 A period of certain groups of the response simulated experimental data

图8　数值仿真流程图 Fig.8 A flow chart of numerical simulation

频域法涉及的Levenberg-Marquardt迭代算法旨在寻找最优参数，涉及初始参数选取。选两组初始参数产生仿真数据，一组产生仿真数据准确模型参数；一组为随机模型参数，即k1=1，k2=0，k3=0.1，b=1，c=1，α=1，γ=1，β=0，n=0。 利用准确初值直接产生原始数据作为真值，采用Ni’s方法识别后产生的数据作为模型数据进行比较。预测响应与真实响应迟滞环见图9～图11。

图9　用精确初值Ni’s方法预测响应迟滞环与真实响应迟滞环 Fig.9 A period of the true responses and the predicted responses hysteresis loops using parameters identified through Ni’s method with exact initial values

图10　用随机初值Ni’s方法预测 响应迟滞环与真实响应迟滞环 Fig.10 A period of the true responses and the predicted responses hysteresis loops using parameters identified through Ni’s method with random initial values

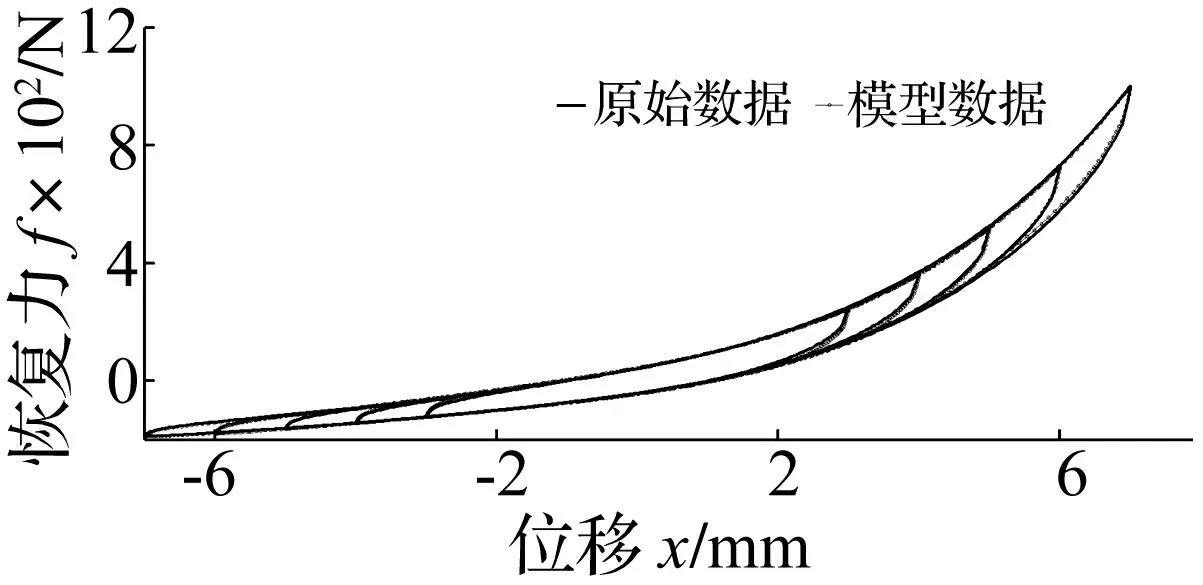
图11　用两阶段识别方法预测 响应迟滞环与真实响应迟滞环 Fig.11 A period of the true responses and the predicted responses hysteresis loops using parameters identified through the two-stage identification method

为定量分析预测效果优劣，利用两数学统计参数对每组仿真预测计算结果见表1。其中RMSE为均方根误差，用于衡量观测值与真值间偏差。RMSE值越小预测响应越接近真实响应。

表1　预测迟滞环的RMSE及R NL

针对非线性模型，更有效的曲线回归拟合优度指标RNL[18]为

(26)

式中：pk为预测离散响应值；fk为测试离散响应值；K为一个稳定周期内离散数据个数。

由式(26)，RNL将残差平方和与相对误差结合，RNL愈接近1表明识别参数拟合的曲线优度愈好。

由图9～图11及表1看出，所有预测迟滞环均非常接近真实迟滞环。而表1的RMSE与RNL值表明，用本文模型及两阶段识别方法较Ni’s模型参数识别时采用随机初值预测真实响应效果好，且仿真试验数据为由Ni’s模型产生。为使Ni’s模型参数收敛至合适的解，需正确选择初始值。数值仿真中尝试随机选取诸多初始值，大多无法收敛至合适的解，且至少超过100次迭代方可获得一个收敛解。而每步的迭代Ni’s方法均需进行傅里叶变换及反变换，因此用该方法耗时较长。而两阶段识别方法不涉及迭代算法，不存在初始参数选取及收敛性问题，因而能提高计算效率。采用Ni’s模型、方法取精确初值所得预测响应较用本文参数识别方法更接近真实响应。此因两阶段法在参数识别第二阶段未涉及优化问题，不能保证识别参数为最优值。

为判断本文参数识别方法的抗噪声能力，在不同噪声水平下进行数值仿真。参数预测见表2。由表2看出，噪声水平越低预测响应越接近真实响应，随噪声水平增加对预测效果影响不大，说明该方法抗噪声能力较强。

表2　不同噪声水平下预测迟滞环的RMSE及R NL

4试验验证

为验证两阶段参数识别方法对O型钢丝绳隔振器动态特性参数识别的有效性，在某汽车研究院MTS弹性元件测试系统(型号831)试验机上用位移激励方式对隔振器动态特性进行试验研究。用本文模型与两阶段参数识别方法所得试验、预测模型迟滞环比较见图12。

图12　用两阶段识别法预测、试验迟滞环 Fig.12 The measured responses and the predicted responses hysteresis loops using parameters identified through the two-stage identification method

采用Ni’s模型、参数识别方法在只有试验迟滞环无精确模型参数情况下,随机选取初始参数k1=1,k2=0,k3=1,b=1,c=1,α=1,γ=1,β=0,n=0，所得试验、预测模型迟滞环比较见图13。

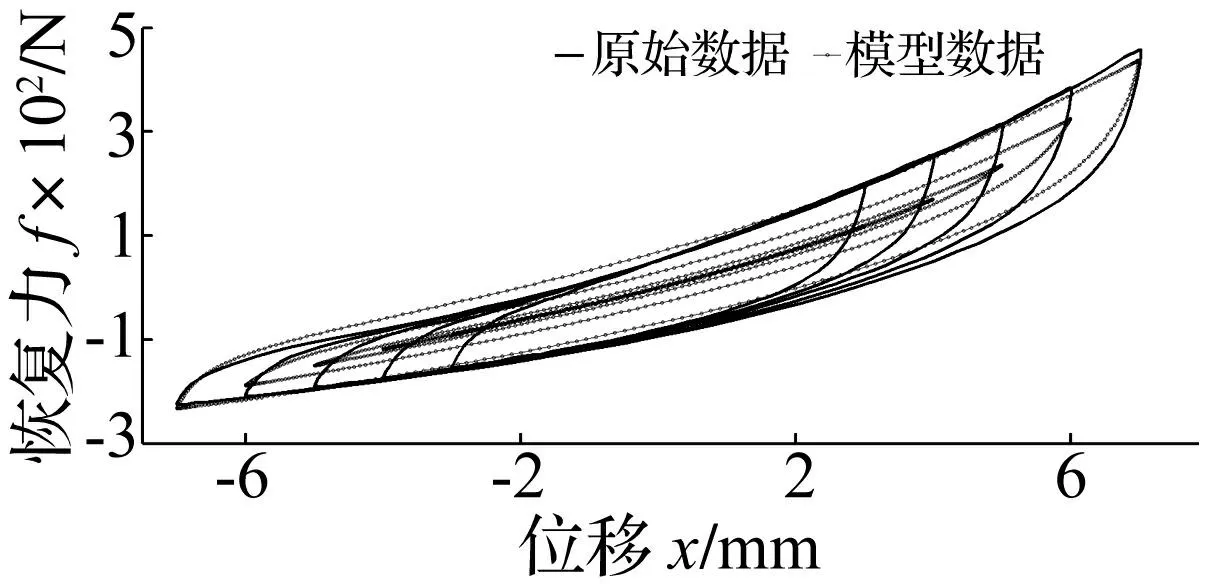
图13　用随机初值Ni’s法预测、试验迟滞环 Fig.13 The measured responses and the predicted responses hysteresis loops using parameters identified through Ni’s method with random initial values

基于试验结果，用Ni’s方法、Ni’s模型参数识别结果及预测效果见表3。

用本文模型与两阶段参数识别方法所得参数识别结果及预测效果见表4。由图12、图13及表3、表4看出，用改进归一化Bouc-Wen模型及两阶段法所得预测、试验迟滞环吻合较好，用Ni’s模型及其频域法在不知精确模型参数情况下随机选取模型参数初始值所得预测、真实响应间差距较大，虽用诸多随机初始值，但有些情况不能获得模型参数值，无法预测响应。

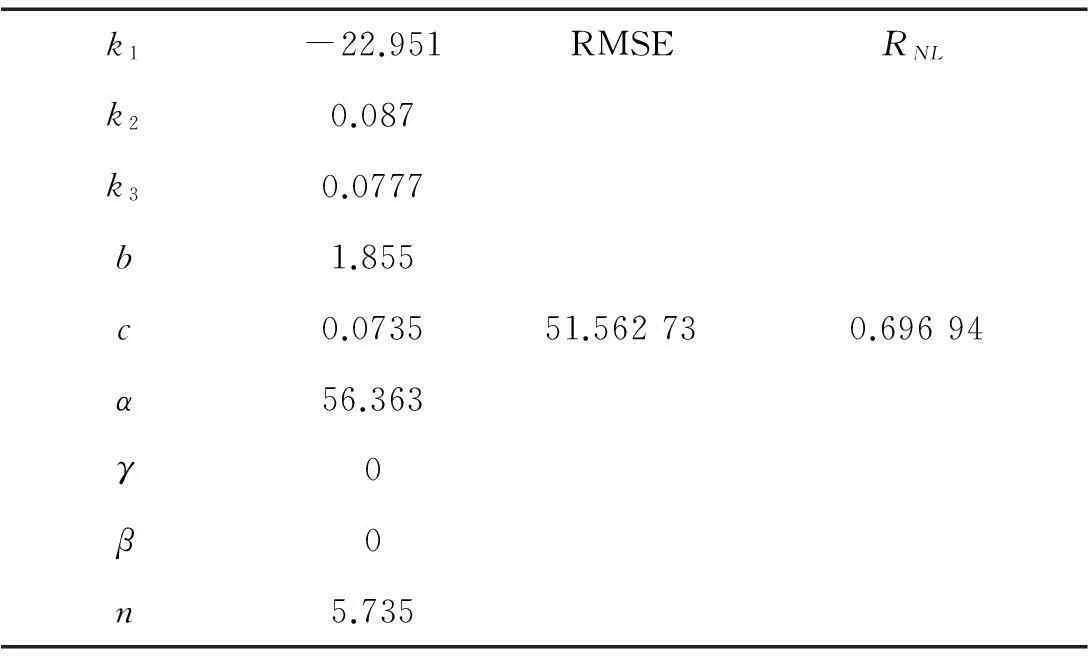
表3　用Ni’s识别方法Ni’s模型参数识别结果

表4　采用两阶段识别方法本文模型参数识别结果

5结论

通过理论分析及数值仿真、试验验证，研究分析两阶段参数识别方法，结论如下：

(1)两阶段法可准确有效识别出O型钢丝绳隔振器模型参数，预测响应接近真实响应；该法对噪声污染不敏感，虽信号被噪声严重污染，待识别模型参数可能偏离其真值，但用识别参数产生的预测迟滞环仍与真实迟滞环一致，认为结果合理。

(2)两阶段参数识别方法试验曲线与模型预测曲线吻合较好，能准确有效描述O型钢丝绳隔振器非对称迟滞环动态特性。该方法在整个参数识别中不涉及迭代算法，使参数识别顺利进行，且能提高识别的准确性。

(3)该方法在识别程序中未考虑优化问题，不能保证所得模型参数为最优值。若想获得最优值，可先用该方法获取参数值作为初始值，再用传统迭代算法求解，快速获得收敛值。

参考文献

[1]Massa G D, Pagano S, Rocca E,et al. Sensitive equipments on WRS-BTU isolators[J]. Meccanica,2013, 48:1777-1790.

[2]班书昊,李晓艳,蒋学东,等.钢丝绳隔振器的非线性动力学模型[J].力学与实践,2012,34(1):66-69.

BAN Shu-hao, LI Xiao-yan, JIANG Xue-dong, et al. Nonlinear dynamic model on steel-wire isolator[J]. Mechanics in Engineering,2012,34(1):66-69.

[3]周桐,张思箭,李健.电子器件隔振设计实验研究[J].实验力学,2006,21(3):387-392.

ZHOU Tong, ZHANG Si-jian, LI Jian. A experimental study on isolation design of electronic equipment[J].Journal of Experimental Mechanics, 2006,21(3):387-392.

[4]Demetriades G F,Constantinou M C, Reinhorn A M. Study of wire rope systems for seismic protection of equipment in buildings[J].Engng Structs,1993, 15(5): 321-334.

[5]朱涛,赵科,肖守讷,等.基于动态规划的动载荷时域识别方法研究[J].振动与冲击,2012,31(13):138-146.

ZHU Tao, ZHAO Ke, XIAO Shou-ne,et al. Force identification in time domain based on dynamic programming[J].Journal of Vibration and Shock, 2012, 31(13):138-146.

[6]Zapateiro M, Luo N S. Parametric and non parametric characterization of a shear mode magnetorheological damper[J]. Journal of Vibroengineering,2007, 9(4):14-18.

[7]Kaul S. Multi-degree-of-freedom modeling of mechanical snubbing systems[J].Journal of Vibroengineering, 2011, 13(2):195-211.

[8]Ni Y Q, Ko J M, Wong C W. Identification of non-linear hysteretic isolators from periodic vibration tests[J]. Journal of Sound and Vibration, 1998,217(4): 737-756.

[9]Ni Y Q, Ko J M, Wong C W, et al. Modelling and identification of a wire-cable vibration isolator via a cyclic loading test part 2: identification and response prediction [J]. Journal of Systems and Control Engineering,1999, 213(3):173-182.

[10]唐炜,乔倩,史中科.频域最小二乘辨识方法的参数约束条件选取[J].航空学报,2012,33(12):2253-2260.

TANG Wei, QIAO Qian, SHI Zhong-ke. On the choice of parameter constraint for frequency domain least squares identification[J].ActaAeronautica et Astronautica Sinica, 2012,33(12):2253-2260.

[11]Yin Q, Zhou L, Mu T F,et al. System identification of rubber-bearing isolators based on experimental tests[J]. Journal of Vibroengineering,, 2012,14(1):315-324.

[12]Lin J S, Zhang Y G. Nonlinear structural identification using extended Kalman filter[J]. Computers& Structures, 1994, 52(4):757-764.

[13]Roberts J B, Sadeghi A H. Sequential parametric identification and response of hysteretic oscillators with random excitation[J]. Struct. Safety, 1990, 8:45-68.

[14]李理敏,龚文斌,刘会杰,等.基于自适应扩展卡尔曼滤波的载波跟踪算法[J].航空学报,2012,33(7):1319-1328.

LI Li-min, GONG Wen-bin, LIU Hui-jie,et al.A carrier tracking algorithm based on adptive extended kalman filter[J].Acta Aeronauticaet Astronautica Sinica, 2012,33(7): 1319-1328.

[15]Ikhouane F, Rodellar J. On the hysteretic Bouc-Wen model-part I: forced limit cycle characterization[J]. Nonlinear Dynamics, 2005, 42(1): 63-78.

[16]Ikhouane F, Gomis-Bellmunt O. A limit cycle approach for the parametric identification of hysteretic systems[J]. Systems & Control Letters,2008, 57(8):663-669.

[17]Ni Y Q, Ko J M, Wong C W,et al. Modelling and identification of a wire-cable vibration isolator via a cyclic loading test, part 1: experiments and model development[J]. Proceedings of the Institution of Mechanical Engineers, Journal Systems and Control Engineering,1999, 213(3): 163-171.

[18]张世强.曲线回归的拟合优度指标的探讨[J].中国卫生统计,2002,19(1):9-11.

ZHANG Shi-qiang. Approach on the fitting optimization index of curve regression[J].Chinese Journal of Health Statistics, 2002,19(1):9-11.