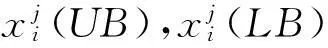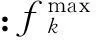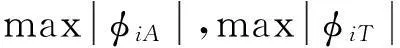多目标快速群搜索优化算法及在模型修正中的应用

第一作者李世龙男，博士生，1987年生

通信作者马立元男，教授，博士生导师，1962年生

多目标快速群搜索优化算法及在模型修正中的应用

李世龙，马立元，李永军，王天辉

(军械工程学院导弹工程系，石家庄050003)

摘要：为解决群搜索算法在求解多目标优化问题时易陷于局部最优或过早收敛，限制其在复杂结构模型修正中的应用问题，提出改进的群搜索优化算法-多目标快速群搜索优化算法(MQGSO)。采用LPS搜索方法对发现者进行迭代更新，能使发现者更快到达最优位置，提升寻优效率；对追随者增加速度更新机制，考虑其自身历史最优信息以保证收敛精度，并在算法后期采用交叉变异策略增加追随者个体多样性，避免陷入局部最优；在游荡者迭代更新中引入分量变异控制策略，增加其搜索的随机性，提高算法的全局寻优性能。通过7个典型多目标优化测试函数及某发射台有限元模型修正实例，对算法性能进行验证分析。结果表明，与已有MPSO(Multi-objective Particle Swarm Optimization)及MBFO(Multi-objective Bacterial Foraging Optimization)两种算法相比，所提MQGSO算法搜索性能更强、收敛速度更快、计算精度更高，不失为求解复杂多目标优化问题的有效方法。

关键词：多目标优化；群搜索算法；Pareto最优解；模型修正；目标函数

基金项目：军队科研资助项目([2012]80)

收稿日期：2014-11-27修改稿收到日期：2015-04-17

中图分类号:TB123；TU311

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.20.021

Abstract:Model updating is a typical multi-objective optimization problem. Comparing with other traditional swarm intelligent algorithms, the group search optimization (GSO) algorithm has outstanding performance on solving complex optimization problems. However, it is not free from the problems such as being entrapped into a local optima and premature convergence when it is utilized in multi-objective optimization. A novel multi-objective quick group search optimizer by the name of MQGSO was proposed for solving these problems. To simplify the computation, the LPS method was introduced in updating producers. Meanwhile, the particle swarm optimization (PSO) evolutionary strategy was adopted in updating scroungers to improve the convergence accuracy. Moreover, to restrict fallng into local optima, a crossover and mutation operation was introduced to increase the diversity of scroungers in each iteration. In addition, mutation probability, which can increase the randomicity of rangers, was introduced to enhance the global searching capability. Seven multi-objective minimization benchmark functions and a model updating case of a certain launch platform were used to evaluate the proposed MQGSO against MPSO and MBFO algorithms. The calculation results show that the MQGSO has a preferable convergence rate and accuracy, and it is an effective method for multi-objective optimization.

Multi-objective quick group search optimization algorithm and its application in model updating

LIShi-long,MALi-yuan,LIYong-jun,WANGTian-hui(The 4st Department, Ordnance Engineering College, Shijiazhuang 050003, China)

Key words:multi-objective optimization; group search optimizer(GSO); Pareto optimal solution; model updating; objective function

多目标优化(Multi-objective Optimization)作为理论研究与工程实践中常见的一类优化问题，其主要特点为各目标相互冲突、此消彼长，最优解通常不是唯一确定，而是一个解集，也称Pareto最优解集[1]。求取Pareto最优解集的常用方法为传统算法与进化算法两类。传统算法将MOP问题转化为多个不同的单目标优化问题求解，如目标规划法、层次优化法、全局准则法及多目标加权法等[2]。传统算法虽可利用已成熟的单目标优化算法，但对Pareto前端为非凸情形，则不能求出Pareto最优解集，且计算量较大。进化算法(Evolutionary Algorithm，EA)因搜索具有多向性及全局性，并可同时处理大规模搜索空间，具有一定优势。

对多目标进化算法研究较多，如Deb等[3]提出NSGA-Ⅱ，Knowles等[4]提出PAES，Zitzler等[5]提出SPEA-Ⅱ等。另外，出现的改进算法亦有种群进化过程改进及与其它算法混合两类，具有代表性的包括段绪伟等[6]提出的改进算法及Virginia等[7]提出的杂交算法等。而群智能算法(Swarm Intelligence，SI)获得快速发展，使多目标优化问题求解又增新途径。如何应用诸多方法求解复杂的多目标优化问题成为各领域研究新热点。Debarati等[8]将人工杂草算法引入多目标优化问题求解，通过与典型进化算法对比分析证明其优越性。Mahmoud等[9]采用改进的模拟退火算法对典型多目标优化函数进行测试分析表明，收敛速度较快，且具有较好鲁棒性。Zhao等[10]提出的多目标粒子群优化算法(Multi-objective Particle Swarm Optimization，MPSO)，具有较好的寻优效果。Niu等[11]提出多目标细菌觅食优化算法(Multi-objective Bacterial Foraging Optimization，MBFO)，结果表明，较NSGA-Ⅱ等能更准确获得Pareto最优解集。

受自然界动物群居生活及搜索行为启发，基于PS(producer-scrounger)模型，He等[12-13]提出全新的群智能算法-群搜索优化算法(Group Search Optimizer，GSO)。与较经典ACO、PSO算法相比，GSO算法在解决高维复杂优化问题方面体现出显著优势。而至今，将GSO算法用于多目标优化问题求解研究未见报导，此为本文研究目的所在。

模型修正属典型的多目标优化问题。GSO算法在求解多目标优化问题时易陷于局部最优或过早收敛，从而限制其在复杂结构模型修正中的应用。为此，本文提出多目标快速群搜索优化算法(Multi-objective Quick Group Search Optimizer，MQGSO)，与已有MPSO、MBFO算法相比，搜索性能更强、收敛速度更快、计算精度更高，并通过7个典型多目标优化测试函数分析及某发射台有限元模型修正实例，证明算法的先进性及有效性。

1多目标优化问题

多目标优化问题可描述为求解一组决策向量，使其在满足约束条件情况下实现多目标函数的最优化，数学表达式为

式中：F(X)为由k个目标函数构成的目标向量；X=[x1,x2,…,xn]T为n维决策变量；g(X)，ρ(X)分别为不等式、等式约束条件。

多目标优化中因各目标函数存在相互制约，因此难以同时达到最优。多目标优化问题解往往非单一，而为一个解集，其解无法简单区分优劣。因此需找出对各目标均最优的解。Pareto占优方法如下。

定义1Pareto支配关系

针对最小化问题，设u=(u1,u2,…,un)T及v=(v1,v2,…,vn)T为两个目标向量，若对所有目标函数∀i={1,2,…,k}均有fi(u)≤fi(v)且u≠v，则称uPareto支配v。

定义2Pareto解集与Pareto前沿

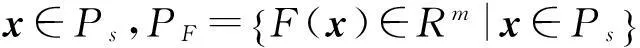
2群搜索优化算法

在标准GSO算法中，个体迭代更新执行一种角度搜索机制。设种群在n维空间中搜索，则第i个体在第k次迭代中的位置可表示为

(2)

式中：M为种群个体总数，其搜索角度为n-1维矢量，即

(3)

对搜索角度做笛卡尔坐标变换为

(4)

通过将前n-td-1个接近0的元素直接置零，在不影响搜索能力的同时可提高计算效率。通过式(4)转换，得个体i的搜索方向为

(5)

GSO种群中的个体被分为发现者、追随者、游荡者三类，在每次迭代计算中，每个体均有机会扮演该三种角色，其迭代更新机制[15]如下。

2.1发现者

每次迭代中，将适应度函数值最佳个体作为发现者，对其正前方、右侧、左侧进行扫描探测，即

(6)

(7)

式中：Uj，Lj分别为第j维搜索方向上下边界。

将3个随机探测的位置与发现者当前位置进行比较，若有更优位置，则发现者跳至该位置，否则保持原位置不变，并调整其搜索方向，即

φk+1=φk+r2αmax

(8)

式中：αmax为最大搜索转角。

若经m次迭代后发现者仍未找到更优位置，则其搜索角度调整至0°，即

φk+m=φk

(9)

式中：m为设定的常数。

2.2追随者

种群中大部分个体被选为追随者，若个体i在第k次迭代中被选为追随者，则向发现者靠拢，即

(10)

式中：r2∈Rn-1为在[0,1]间均匀分布的随机数序列。加入者位置更新后按式(8)调整其搜索方向。

2.3游荡者

若个体i在第k次迭代中被选为游荡者，则其将在群体周围随机游荡。按式(8)确定搜索方向，按式(11)确定随机搜索步长，按式(12)移动至新位置。

li=br1lmax

(11)

(12)

3多目标快速群搜索优化算法

将标准GSO算法用于多目标模型修正时，由于参加迭代修正的参数种类、个数众多，导致种群规模较大且收敛条件复杂，算法易陷入局部最优或过早收敛，难以获得全局最优解。MQGSO算法对发现者、追随者及游荡者个体更新策略进行改进，可大大提高在求解多目标优化问题中的收敛效率及精度。

3.1发现者LPS更新策略

在标准GSO算法中，发现者采用角度搜索策略，由于需进行从极坐标到笛卡尔坐标转换，会耗费大量计算时间。另外，最大搜索角度常设为π/a2，因转换为非线性，故不同维数搜索尺度也不同[16]。事实上，发现者的搜索为围绕最优解的局部搜索行为，此搜索策略可转换为在极坐标中的模式搜索。为充分减小计算量并提高发现者的局部搜索能力，本文引入LPS(Limited Pattern Search)[17]搜索方法至发现者搜索计算中。与基于角度搜索的扫描策略相比，LPS方法不受初始搜索角度φi的限制，能使发现者更快到达最优位置。

从种群Sk中随机选择m个点作为Poll中心的候选点，将其中一个点作为第k次计算的Poll中心xk。以xk为中心，定义Poll组为

(13)

式中：Δk为搜索步长，大小与m个Poll中心候选点间平均距离avgdis有关；ei为第i个成员所在位置坐标。

LPS对所有yi∈pk逐个评估，直至找到适应度较f(xk)更高的点。具体步骤为：①从种群Sk中随机选m个较分散的点，一般取m=10%×Sk；②计算m个点的平均距离avgdis，并取Δk=0.1×avgdis；③将m个点中适应度最好的点作为Poll中心xk；④计算yi=xk+Δkdi，若存在yi∈pk，使f(yi)

3.2追随者迭代更新策略

标准GSO算法中，追随者始终以随机步长向发现者靠拢，当迭代计算进入中后期时易出现寻优速度变慢或陷入局部最优。本文将PSO算法的速度更新策略引入追随者个体位置中，并考虑个体自身历史最优信息，即

随迭代次数t的增加，速度的惯性权重不断减小，追随者搜索步长随之减小。由于考虑追随者自身的历史最优信息，有利于提升算法的收敛速度及精度。

算法进入中后期(t>T0)，追随者速度不断减小，个体易出现惰性，导致大部分追随者在局部极小值附近不断聚集，会使算法早熟收敛。为此，本文引入遗传算法中交叉变异策略增加追随者个体的多样性，使算法能跳出局部极小值。

3.2.1交叉策略

每次迭代中，计算每个体基于当前位置的适应度，并对适应度值进行排序，选择适应度较低的M个个体，两两随机组合进行交叉操作，即

(15)

式中：x为D维位置向量；childk(x)，parentk(x)(k=1，2)分别为交叉后生成的新个体及原始个体；p为D维均匀分布的随机数向量。

交叉概率的每个分量均在[0,1]上取值，将交叉后生成的新个体与原始个体一起按适应度高低进行排序，并从中选M个适应度高的个体与未交叉个体组成新种群，进入下一次迭代计算。

3.2.2变异策略

变异的两关键点为确定时机、选择策略。若连续经K次迭代计算发现者变化Δp≤Δp0，则算法执行变异操作。在追随者中随机选N个个体，利用高斯算子进行变异，即

(16)

将变异生成的N个新个体与未变异个体共同组成新种群，进入下一次迭代计算。

3.3游荡者分量变异控制策略

标准GSO算法中，游荡者以随机角度及步长进行独立搜索。由于未能充分利用搜索中的有利信息，算法后期易陷入局部极小值。尤其在局部、全局极小值相距较远时，算法较难跳出局部极小值。为此，本文引入分量变异控制策略，控制允许变异的维数量，使其随迭代逐渐递减以提高收敛速度。同时，在个体生成新位置时，以随机方式确定所用正负数比例，增加随机性，提升算法全局寻优性能。

在第k次迭代中，第i个体具体更新方法为

(1)计算个体分量变异概率(Mutation Probability，MP)

MP=1.5/n+(4n/k)2

(17)

迭代计算初期，分量变异概率取值较大，可提高算法的全局搜索能力；迭代后期，分量变异概率取值变小，使算法的局部搜索能力增强。

(2)计算个体变异向量大小

(18)

式中：maxstep=UB-LB为每个维度允许的最大步长，UB，LB分别为变量上下界；mod为MATLAB求余运算；randn(n,1)为服从标准正态分布的n维随机向量。

(3)以随机方式确定变异向量维的标志位

(19)

式中：mutflag为允许变异维的标志位；ones(n,1)为所有元素为1的n维向量；rand(1)为在[0,1]区间均匀分布的随机数；<为比较左边各分量与右边标量大小后返回布尔值向量。

(4)更新个体位置

3.4算法步骤

4算法性能测试

4.1测试函数

用7个典型多目标优化函数[19]对算法性能进行测试，具体如下：

(1)SCH函数

f1(x)=x2,f2(x)=(x-2)2

(21)

式中：x∈[-1 000,1 000]。

(2)FON函数

(22)

式中：xi∈[-4,4];i=1,2,3。

(3)POL函数

(23)

式中：xi∈[-π,π];i=1,2。

(4)KUR函数

(24)

式中：xi∈[-5,5]；i=1,2,3。

(5)ZDT1函数

(25)

式中：xi∈[0,1]；i=1,2,…,n;n=30。

(6)ZDT2函数

(26)

式中：xi∈[0,1]；i=1,2,…,n;n=30。

(7)ZDT3函数

(27)

式中：xi∈[0,1]；i=1,2,…,n;n=30。

7个测试函数均含两个目标函数。为研究本文方法的先进性及有效性，将MQGSO算法与MPSO、MBFO算法进行对比分析。为增强可比性，所有公共参数设置均相同，种群个数N=100，全局迭代次数Tmax=1 000。

4.2评价指标

引入两个指标评价3种算法的优化效果。

4.2.1收敛性指标

(28)

收敛性指标定义为

(29)

C(A)值越小，说明计算解集与Pareto最优解集平均距离越小，算法收敛性越好。

4.2.2多样性指标

多样性指标用于评价计算解集沿Pareto前沿分布的均匀程度，一个好的解集应均匀分布在整个Pareto前沿而不陷入前端某个局部。各解之间最小距离为

(30)

多样指标定义为

(31)

S(A)值越小，说明计算解集分布越均匀。

4.3结果分析

利用同一初始种群，分别用3种算法对每个测试函数运行30次，两个评价指标统计结果见表1、表2，包括均值及标准差两项。由两表看出，MQGSO算法在解集的收敛性及多样性表现均优于MPSO、MBFO算法。

表1　收敛性指标均值及标准差对比

表2　多样性指标均值及标准差对比

图1 ZDT1的Pareto前沿Fig.1ParetofrontofZDT1图2 ZDT2的Pareto前沿Fig.2ParetofrontofZDT2图3 ZDT3的Pareto前沿Fig.3ParetofrontofZDT3

限于篇幅，仅给出3种算法在ZDT1、ZDT2、ZDT3上所得Pareto前沿，见图1～ 图3。由3图看出，MQGSO算法在ZDT1、ZDT2、ZDT3上所得Pareto前沿与真实Pareto前沿最接近，MBFO算法效果次之，MPSO算法差距最大。

由此知，较MPSO、MBFO两种算法，本文MQGSO算法性能更优越，更适合求解复杂的多目标优化问题。

5模型修正

5.1模型介绍及有限元建模

图4　某发射台结构图 Fig.4 Mechanical structure of the launch platform

某发射台主要由焊接骨架、回转部、三角框及千斤顶组成，采用铰接形式与发射车连接，三点铰接于发射车车尾主梁，见图4。

图5　发射台有限元模型 Fig.5 Finite element model of the launch platform

据发射台结构特点，对各结构控制数据进行参数化表达(忽略对发射台刚度、模态特性影响较小的零件及结构特征)，利用ANSYS软件平台编写发射台有限元建模的通用命令流程序。其中，回转部、千斤顶盖简化为质量单元，发射台与发射车的铰接部分(对发射台模态影响较大)建模用solid45单元，其余用beam189单元。所建发射台有限元模型见图5，共含216个梁单元、4个质量单元及15936个实体单元。材料弹性模量E=2.07×1011N/m2，泊松比μ=0.27，密度ρ=7 800 kg/m3。

5.2模态测试及模态匹配

模态测试中，因发射台固定在发射车上，故对其进行约束模态试验。考虑测试信息信噪比较高，测点选响应较大位置，且适当远离所需振动模态节点位置。为区分频率相近的对称、反对称模态，传感器对称布置，避免靠近结构边界[20]。测点布置方案见图6。

图6　发射台测点布置方案 Fig.6 Test location assignment of the launch platform

图7　模态测试现场 Fig.7 The modal experiment scene

分别采用激振器、力锤对结构进行激励，单点激励多点响应。在两种激励方式下分别进行多次重复测试，选测试较稳定的数据组以减小人为操作误差影响。采样频率10 kHz，每个响应信号取20 000个采样点。加速度信号经电荷放大器进入DH5920动态信号测试分析系统，采用东华模态分析软件(DHMA)。模态测试现场见图7。

经模态匹配，初始有限元模型计算模态与试验模态对比见表3。由表3看出，两种激励方式的实测模态相差不大，但有限元模型计算模态与激振器激励的实测模态更接近，因此模型修正以实测模态参数为基准。前4阶模态对比中，初建的有限元模型频率、振型误差较大，需修正。

5.3模型修正及结果分析

基于频率及振型MAC值残差，建立多目标优化目标函数为

(32)

基于式(32)，分别采用MPSO、MBFO及本文MQGSO 计3种多目标优化算法对发射台初始有限元模型进行修正。由于发射台结构复杂，造成有限元模型误差因素众多，本文采用两步修正法。

表3　初始有限元模型计算模态与试验模态的比较

5.3.1初步修正

图8　初步修正中各待修正单元组分布 Fig.8 Distribution of under updated elements group in initial modal updating

初步修正中，各待修正单元组分布及编号见图8，共24个待修正参数，包括弹性模量(E1…E10)、密度(D1…D10)及质量单元(M1…M4)。

采用3种优化算法对各待修正参数迭代修正。设最大迭代进化次数Tmax=1 000，初步修正后有限元模型计算模态与实测模态对比见表4。由表4看出，初步修正后MQGSO算法所得频率误差显著减小，平均误差由11.77%降至8.13%，振型MAC值显著提高；好于MPSO、MBFO算法修正效果，频率平均误差分别降至10.35%及9.76%，振型MAC值提升不大。

图9　精细修正中各待 修正单元组分布 Fig.9 Distribution of under updated elements group in accurate modal updating

5.3.2精细修正

发射台骨架为钢管焊接结构，焊缝及周围区域材料特性变化较大，因此焊接点的材料特性为有限元模型误差主要来源。该模型的弯曲部位用冷加工方法完成，该部分会产生加工硬化，硬化部位材料特性变化亦为有限元模型误差来源。综合两因素，精细修正中各待修正子结构分布及编号见图9，含11个焊接点、6个加工硬化子结构，共34个待修正参数，即弹性模量(E1，E2，…，E17)及密度(D1，D2，…，D17)。

表4　有限元模型计算模态与实测模态对比

表5　精细修正后有限元模型计算模态与实测模态对比

精细修正后有限元模型计算模态与实测模态对比见表5。由表5看出，采用MQGSO算法修正的模型精度提升显著，最大频率误差能控制在5%以内，且最小振型MAC值达到0.807，修正后模型可作为损伤识别基准有限元模型；MBFO算法修正效果欠佳，最大频率误差为6.25%，最小振型MAC值为0.714；MPSO算法最差，第4阶频率误差超过8%，最小振型MAC值仅为0.663。

6结论

本文多目标快速群搜索优化算法(MQGSO)能解决标准GSO算法在多目标优化模型修正中应用难的问题。经研究分析，结论如下：

(1)用LPS搜索算法对发现者进行迭代更新，能使其更快到达最优位置，可提升算法的寻优效率。

(2)对追随者增加速度更新，并考虑其自身历史最优信息，利于提高算法的收敛精度。在计算后期采用交叉变异策略增加追随者个体多样性，能有效避免算法陷入局部最优值。

(3)在游荡者迭代更新中引入分量变异控制策略，能增加搜索随机性，提高算法的全局寻优性能。

(4)通过7个典型多目标优化测试函数及某发射台有限元模型修正实例分析表明，本文MQGSO算法搜索性更强能、收敛速度更快、计算精度更高，为求解复杂多目标优化问题的有效方法。

参考文献

[1]Sorensen K,Springael J. Progressive Multi-objective optimization[J]. International Journal of Information Technology & Decision Making, 2014, 13(5): 1617-1619.

[2]Tan K C, Goh C K, Mamun A A, et al. An evolutionary artificial immune system for Multi- objective optimization[J]. European Journal of Operational Research, 2008, 187(2): 371-392.

[3]Deb K, Pratap A, Agarwal S, et al. Evolutionary Multi-objective optimization[J]. European Journal of Operational Research, 2007, 181(3): 1617-1619.

[4]Knowles J, Corne D W. Approximating the nondominated front using the Pareto archived evolution strategy[J]. Evolutionary Computation, 2000, 8(2): 149-172.

[5]Zitzler E, Laumanns M, Thiele L. Spea2:improving the strength pareto evolutionary algorithm[R]. Zurich: Computer Engineering and Networks Laboratory (TIK), 2001.

[6]段绪伟,李以农,郑玲,等. 基于NSGA-Ⅱ遗传算法的磁流变悬置多目标优化[J]. 振动与冲击,2014,33(3): 191-196.

DUAN Xu-wei, LI Yi-nong, ZHENG Ling, et al. Multi-objective optimization for a MR engine mount based on NSGA-Ⅱ algorithm[J]. Journal of Vibration and Shock, 2014, 33(3): 191-196.

[7]Yannibelli V, Amandi A. Hybridizing a Multi-objective simulated annealing algorithm with a Multi-objective evolutionary algorithm to solve a Multi-objective project scheduling problem[J]. Expert Systems with Applications,2013, 40(7): 2421-2434.

[8]Kundu D, Suresh K, Ghosh S, et al. Multi-objective optimization with artificial weed colonies[J]. Information Sciences,2011, 181(12): 2441-2454.

[9]Alrefaei M H, Diabat A H. A simulated annealing technique for Multi-objective simulation optimization [J]. Applied Mathematics and Computation,2009, 215(8): 3029-3035.

[10]Zhao Z G, Li T S, Yang L F. Particle swarm optimization for Multi-objective programming problems[J]. Computer Engineering and Applications, 2009, 45(29): 37-40.

[11]Niu Ben,Wang Hong, Wang Jing-wen, et al. Multi-objective bacterial foraging optimization[J]. Neurocomputing,2013, 116(12): 336-345.

[12]He S, Wu Q H, Saunders J R. A novel group search optimizer inspired by animal behavioral ecology[C]. IEEE Congress on Evolutionary Computation,2006: 1272-1278.

[13]Yan X, Yang W, Shi H. A group search optimization based on improved small world and its application on neural network training in ammonia synthesis[J]. Neurocomputing,2012, 97(15): 94-107.

[14]张冬梅,龚小胜,戴光明,等. 求解复杂多目标优化问题MOEA/D-GEP算法[J]. 华中科技大学学报:自然科学版, 2012, 40(4): 33-36.

ZHANG Dong-mei, GONG Xiao-sheng, DAI Guang-ming, et al. MOEA/D-GEP algorithm solving expensive Multi-objective optimization problems[J]. Journal of Huazhong University of Science and Technology:Natural Science Edition,2012,40(4): 33-36.

[15]刘锋,覃广,李丽娟. 快速群搜索优化算法及其应用研究[J]. 工程力学, 2010, 27(7): 38-44.

LIU Feng, QIN Guang, LI Li-juan. A quick group search optimizer and its application research[J]. Engineering Mechanics,2010, 27(7): 38-44.

[16]He S, Wu Q H, Saunders J R. Group search optimizer: an optimization algorithm inspired by animal searching behavior[J]. IEEE Transactions on Evolutionary Computation,2009,13(5): 973-990.

[17]Ali M M, Kajee-Bagdadi Z. A local exploration-based differential evolution algorithm for constrained global optimization[J].Applied Mathematics and Computation, 2009,208(1): 31-48.

[18]Deb K, Amrit P, Agarwal S, et al. A fast and elitist Multi-objective genetic algorithm-NSGA-II[J]. IEEE Transactions on Evolutionary Computation,2002,6(2): 182-197.

[19]Wang Ling, Zhong Xiang, Liu Min. A novel group search optimizer for Multi-objective optimization[J]. Expert Systems with Applications,2012,39(2):2939-2946.

[20]李世龙,马立元,李永军,等. 基于模型修正的钢管焊接结构焊缝损伤识别[J]. 振动与冲击, 2012, 31(15): 127-131.

LI Shi-long, MA Li-yuan, LI Yong-jun,et al. Damage detection for weld seam on steel tube welded structures based on model updating[J]. Journal of Vibration and Shock, 2012, 31(15): 127-131.