计算δ函数势阱中平均动能的方法
2016-01-12李明明刘海英济南大学物理科学与技术学院山东济南250022
李明明,刘海英(济南大学物理科学与技术学院,山东济南 250022)
计算δ函数势阱中平均动能的方法
李明明,刘海英
(济南大学物理科学与技术学院,山东济南250022)
摘要:用量子力学基本公式F=∫ψ*F^ψdτ计算粒子在δ势阱中运动的平均动能时,结果为负,这是由求解δ势阱中运动方程的特殊方法造成的。采用由解定态方程得到的定态能量减去平均势能得到平均动能的新方法,计算公式为T= E-∫ψ*Vψdτ。并研究了粒子在势阱V( r) =-γδ( r-a)基态的平均动能。
关键词:δ势阱;平均动能;维里定理
在量子力学中,计算粒子的力学量F^平均值F—是一个核心问题[1-7],其计算公式[8]为:

式中:ψ是粒子的归一化波函数;ψ*是ψ的复共轭。
在微观领域中,δ函数势阱是一种反映微观现象共同特征的常用的理想模型[9-12]。然而,当粒子处于δ函数势阱束缚定态时,用式( 1)算出的平均动能是负的。这说明式( 1)不能用来计算δ函数势阱中粒子的动能。鉴于此,本文提出了一种函数势阱中粒子的平均动能的计算方法,并讨论了式( 1)为负的原因。
1 在势阱V( x) =-γδ( x)中的定态能量和波函数
粒子波函数ψ( x)满足的定态方程为:
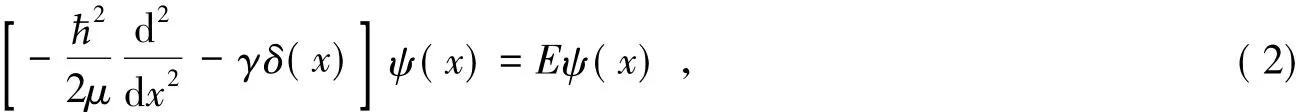
式中:μ为粒子的质量; E为束缚态能量;γ为代表δ势阱强度的常数;为普朗克常数。
式( 2)存在束缚态的条件是E<0。令
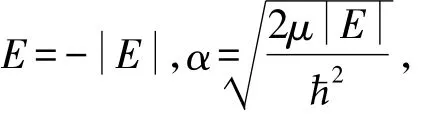
式( 2)变为

求解式( 3)的方法是去掉势能发散点x=0,再解方程。在不包含x=0的全部x空间,式( 3)变为

式( 4)的解为ψ=e±ax。式( 4)满足束缚态条件ψ( +∞)及ψ在x=0连续的一般解为

由波函数ψ的归一化条件∫+∞ψ( x)2dx = 1,得A=槡α,则式( 5)可写为:
-∞

式( 6)中α决定粒子的能量E,由ψ'( x)在x=0处的不连续条件[13]
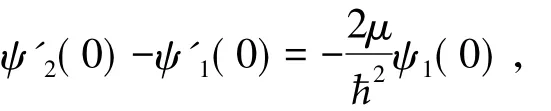
确定为
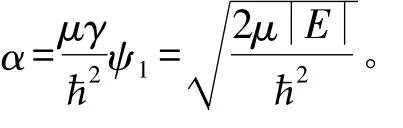
由此得束缚定态能量

将式( 6)代入式( 1),可得:
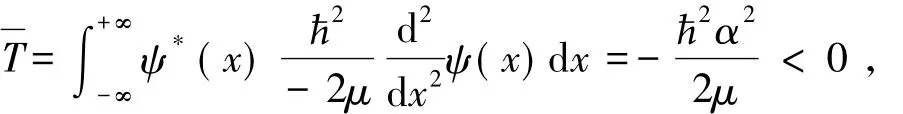
平均动能为负,这显然不对。因此,式( 1)不能用来计算平均动能,同样不能用来计算平均能量,因为
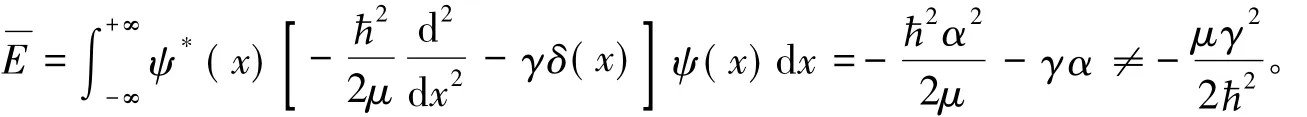
然而,可以证明,式( 1)计算平均势能是正确的:
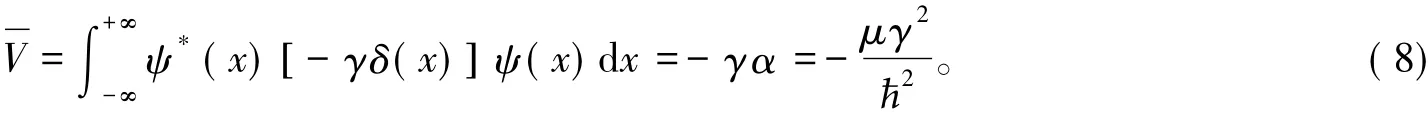
根据维里定理[14],在束缚定态下

如果V( r→)是r→的v次齐次函数,则r→·▽V( r→) = vV( r→),式( 9)写为:

对于V( x) =-γδ( x),V(λx) =-γδ(λx) =λ-1γδ( x) =λ-1V( x),V( x)是x的v=-1的齐次函数。于是,式( 10)改写为:

将式( 8)代入式( 11),得T =μγ2/( 22)。由此得到的能量为:
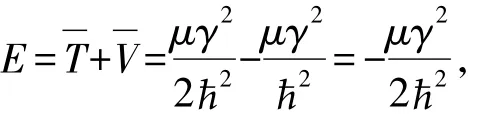
这个结果同式( 7)一致。这就证明了,用式( 1)来计算粒子的平均势能是正确的。因此,正确计算平均动能的方法是由解定态方程得到的定态能量E减去由公式( 1)的算出平均势能V ,得:

由式( 12)算出平均动能T=μγ2/( 22),这是正确的结果。虽然,式( 11)也给出了正确的平均动能,但是式( 11)不具有一般性,如果δ函数势阱形式稍有改变,如改为三维势V(→r) =-γδ(→r-→α),式( 11)就不适用了。而式( 12)具有普遍性,因为它来源于基本的能量公式H=T+V。
2 粒子在势阱V( r) =-γδ( r-a)基态的平均动能
在中心力场V( r) =-γδ( r-a)中,轨道角动量是守恒量。令定态波函数

式中Ylm(θ,φ)为球谐函数。
将式( 13)代入定态方程
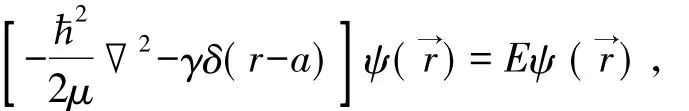
得径向波函数u1( r)满足的方程[15]
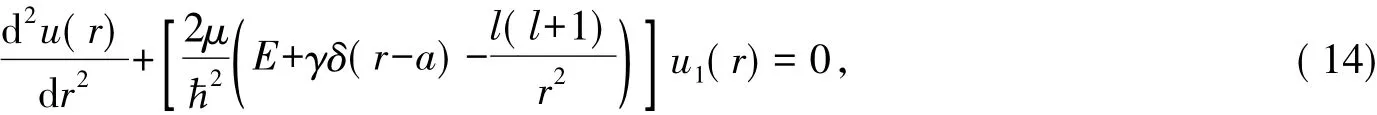
基态必定是l=0的态。令l=0的波函数u0( r)≡u( r)。在式( 14)中,令l=0得u( r)满足的方程
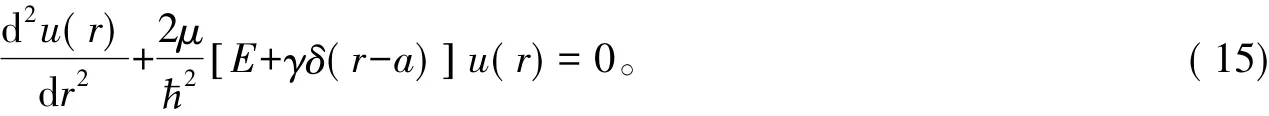
在势阱V( r) =-γδ( r-a)中,要形成束缚态,能量E<0。令
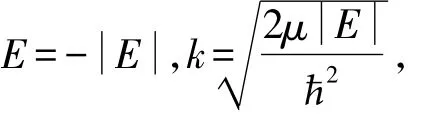
式( 15)变为:
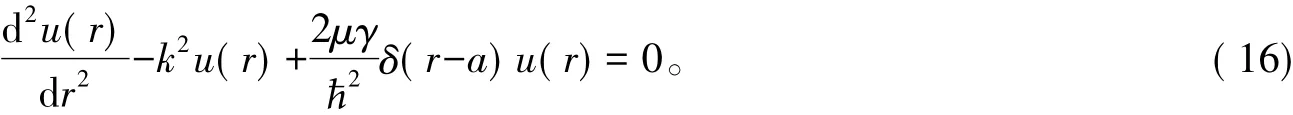
在r≠a的全空间,方程( 17)改写为:

式( 17)的解为u( r) = e±kr。方程( 16)的一般解由ekr与e-kr的线性组合构成,而满足条件u( 0) = 0与u(∞) = 0的解为

由波函数的连续条件u1( a) = u2( a)得B=( e2ka-1) A,代入式( 18),得

于是,l=0的基态波函数为
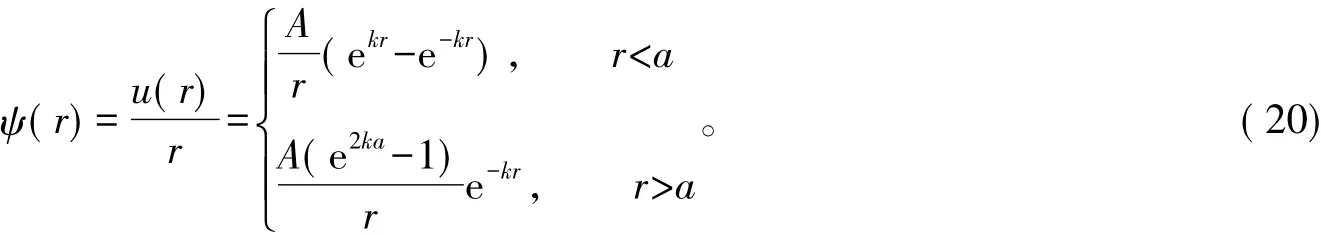
由波函数归一化条件∫∞ψ( r)24πr2dr = 1,得ψ( r)中的归一化常数
0
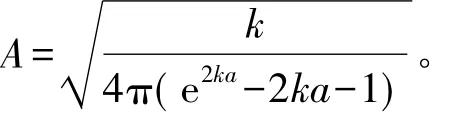
径向波函数一阶导数u'( r)在r=a处的不连续条件为:

波函数k中以及定态能量E决定。将式( 19)代入式( 21),得

式( 22)是k或k中所含定态能量E满足的超越方程。这个方程只能用作图法或数值计算法求解。由作图法得,方程( 22)有解的条件是势阱强度γ>2/( 2μa)。选择势阱强度γ=2/(μa),用数值计算法计算值与定态能量E。令γ=2/(μa),并令x=2ka,式( 22)变为

用数值计算法求得式( 23)的解为x=1.593 6。再由x=2ka=槡2μ E/2,算出
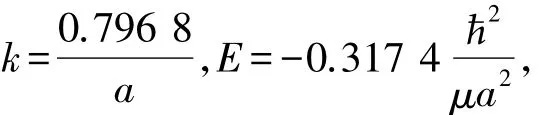
将式( 20)代入式( 1)得
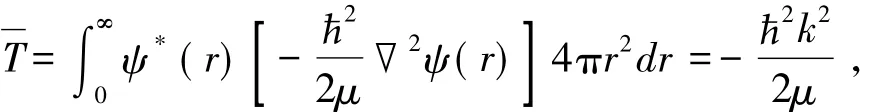
计算出的平均动能是负的。这又一次说明公式( 1)是不适用的,必须用式( 12)计算平均动能。式( 12)中的定态能量E已经求出,E=-0.317 42/(μa2),则平均势能
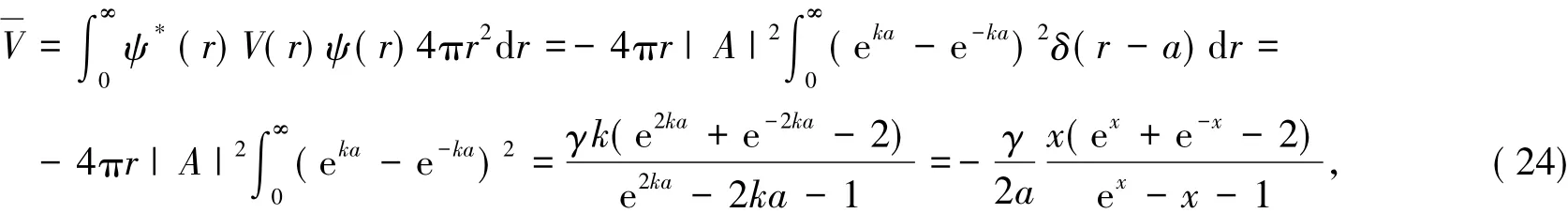
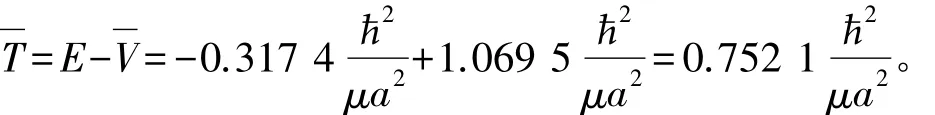
3 讨论
平均动能取负值的原因是由δ势场定态方程的求解方法决定的。以式( 13)为例。由于在此势阱的束缚态能量E<0,令E=-|E|。方程变为
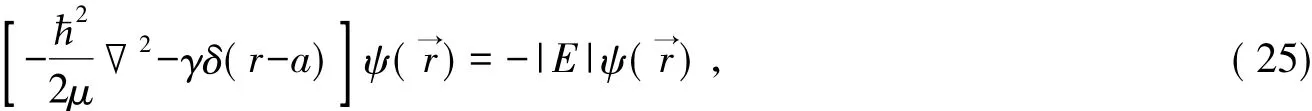
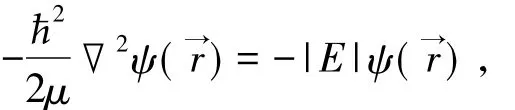
式( 25)含有δ函数,这个方程是无法求解的。为了能求解这个方程,不得不去掉r=a点,在不包括r=a点的空间,方程变为这正是动能算符T=-2▽2/( 2μ)的本征值T=-|E|的本征方程。这就是说,要求解的波函数是动能算符的本征值为-|E|(这也是束缚定态能量)的本征函数E。因此,由这个波函数算出的动能平均值必然是负的。
在求解定态方程时,去掉了势能发散点,因而去掉了δ函数势,却能求出δ函数势中的定态能量。这是因为计算中用到ψ'在势能发散点r=a的不连续条件这个条件是由含有δ函数势的定态方程推导出的。
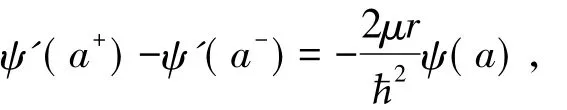
参考文献:
[1]廖荣宝.波函数塌缩问题及物理量期望值表达式的讨论[J].中国科技信息,2011( 21) : 41.
[2]马广清,肖鸿飞.计算力学量平均值的一种方法[J].沈阳大学学报,2005,17( 2) : 98-100.
[3]刘树信.力学量的平均值[J].烟台师范学院学报(自然科学版),1996,12 ( 2) : 153-155.
[4]樊西汉.量子力学平均值计算时应注意的问题[J].临沂师范学院学报,2001,23 ( 4) : 24-26.
[5]高广君.量子力学中力学量的平均值[J].齐齐哈尔师范学院学报(自然科学版),1997,17( 4) : 28-31.
[6]王杰芳,李玉晓,贾瑜,等.量子物理学基本概念的教学研究[J].洛阳理工学院学报(自然科学版),2010,20( 2) : 91-94.
[7]王庆领,张力.算符与量子力学中的力学量[J].新疆师范大学学报(自然科学版),2002,21( 3) : 19-23.
[8]张永德.量子力学[M].2版.北京:科学出版社,2008.
[9]张昆实.量子力学中的势阱问题解析[J].高等函授学报(自然科学版),2005,19( 6) : 17-19.
[10]林琼桂.一维δ势阱中的相对论粒子[J].大学物理,2002,21( 2) : 15-19.
[11]何鸿斌.δ势阱束缚态的一种求法[J].辽宁师范大学学报(自然科学版),1989( 1) : 77-80.
[12]EUGEV Merzbacher.Quantum mechanics[M].Second edition.New York: John Wiley&Sons,Inc,1977: 82-85.
[13]陈鄂生,李明明.量子力学基础教程[M].6版.济南:山东大学出版社,2014.
[14]钱伯初,曾谨言.量子力学习题精选与剖析[M].3版.北京:科学出版社,2008.
[15]曾谨言.量子力学[M].北京:科学出版社,1981.
(责任编辑:郎伟锋)
Method for Calculating Average Value of Kinetic Energy in the Potential Well Function
LI Mingming,LIU Haiying
( School of Physics and Technology,University of Jinan,Jinan 250022,China)
Abstract:In quantum mechanics,the general formula of the average value for physical quantity F^is F= ∫ψ*F^ψdτ.However,it is not valid for the calculation of the kinetic energy of the particle in a δ-function potential well,since it gives a negative value for the kinetic energy,which is caused by the special method of solving the motion equation of the potential well.A new method to obtain kinetic energy is adopted by using the steady state energy obtained by the solution of the steady state equation minus the average potential energy,the function is T = E-∫ψ*Vψdτ.The average kinetic energy of particles in the ground state of the potential well V ( r) =-γδ( r-a) is studied.
Key words:δ-function potential well; average kinetic energy; Virial theorem
作者简介:李明明( 1965—),女,山东寿光人,副教授,主要研究方向为理论物理.
基金项目:济南大学教研项目( W201402)
收稿日期:2015-05-10
DOI:10.3969/j.issn.1672-0032.2015.02.016
文章编号:1672-0032( 2015) 02-0082-05
文献标志码:A
中图分类号:O41
