振动筛激振器的优化

张玉双，闫　畅，张　衡，李　耀，薛　雪，蒋文志(长安大学道路施工技术与装备教育部重点实验室，陕西西安　710064)



振动筛激振器的优化

张玉双，闫畅，张衡，李耀，薛雪，蒋文志
(长安大学道路施工技术与装备教育部重点实验室，陕西西安710064)

摘要:针对直线振动筛激振器要求启动力矩小的特点，建立激振器的数学模型。利用Pro/E软件的敏感度分析寻找较优设计变量并确定它们的取值范围，添加约束条件对激振器进行可行性优化，通过调整激振器的主要几何参数，获得目标函数的最小值及相应的设计变量值。结果表明:和原模型相比，激振器振动筛偏心块转动惯量显著减小，静偏心距基本不变，优化效果显著。

关键词:振动筛;激振器;启动力矩;数学模型;敏感度分析;可行性优化;转动惯量

振动筛作为一种重要的振动机械，主要是利用不同孔径的各层筛网，将颗粒大小不同的混合物料按照所需粒度进行分级，也常用于物料的脱水、脱介和清洗表面的污泥。筛分机械种类繁多，直线式振动筛具有结构简单、成本低廉、功率消耗小及处理量大等优点而广泛应用于矿山、筑路和煤炭等工业工程领域［1－3］。常见的直线振动筛主要由激振器、振源板、侧板、横梁和筛网等组成，其中激振器的主要作用是为振动筛提供所需的激振力。激振力是高速旋转的偏心块所产生的离心力，维持着振动筛的持续振动。激振力增加使得振动强度增大，筛面对物料的作用力加大，物料的速度增大，生产率提高，堵塞率下降［4］。激振力直接影响振动筛的生产率。如果激振器结构设计不合理，可能引起转动惯量偏大，造成启动过程中启动力矩太大，使得振动筛起振困难，因此研究激振器的结构尤为重要。

1　建模

1．1现状

对某5000型沥青搅拌设备用振动筛的试验测试发现:启动过程中，加速度波形发生了明显的震荡现象，图1为其加速度波形图。据分析，这一现象主要是由于激振器启动力矩过大导致的，为了改善这种情况，使振动筛能够平稳启动，本文利用Pro/E软件对现有的激振器结构进行优化。

1．2起振原理

起振过程中偏心块所需起振力矩为:

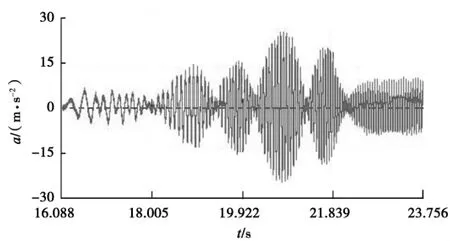
图1振动筛加速度波形图

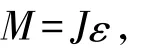
式中: M为起振力矩，N·m; J为激振器转动惯量，kg·m2，J = JC+ mr2，其中，JC表示激振器对于通过质心并且与旋转轴平行的轴的转动惯量，kg·m2; m为激振器的质量，kg; r为质心与旋转轴的距离，m;ε为激振器的角加速度，rad/s2。

激振力F为:

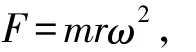
式中ω为激振器的旋转角速度，rad/s。

由式( 1)可知，在ω一定的情况下，F仅与mr有关。

激振器主要有偏心轴式、偏心轮式和偏心块式3种结构，沥青搅拌设备用振动筛的激振器通常为偏心块式［5］。本次进行优化的激振器结构如图2、3所示，采用Q235材料。从图2、3可以看出，该激振器不同于一般的扇形激振器，由主、副偏心块组合而成，结构较为复杂。在主偏心块上加工有和轴相配合连接的通孔和键槽，可以通过轴来传递激振力。主偏心块可划分为3部分，各部分的厚度不一，分别如图2所示的B1、B2、B3，副偏心块的厚度为B4。主副偏心块均开有螺纹孔，两者通过螺栓进行连接。R1～R2为偏习块不同部位的半径。

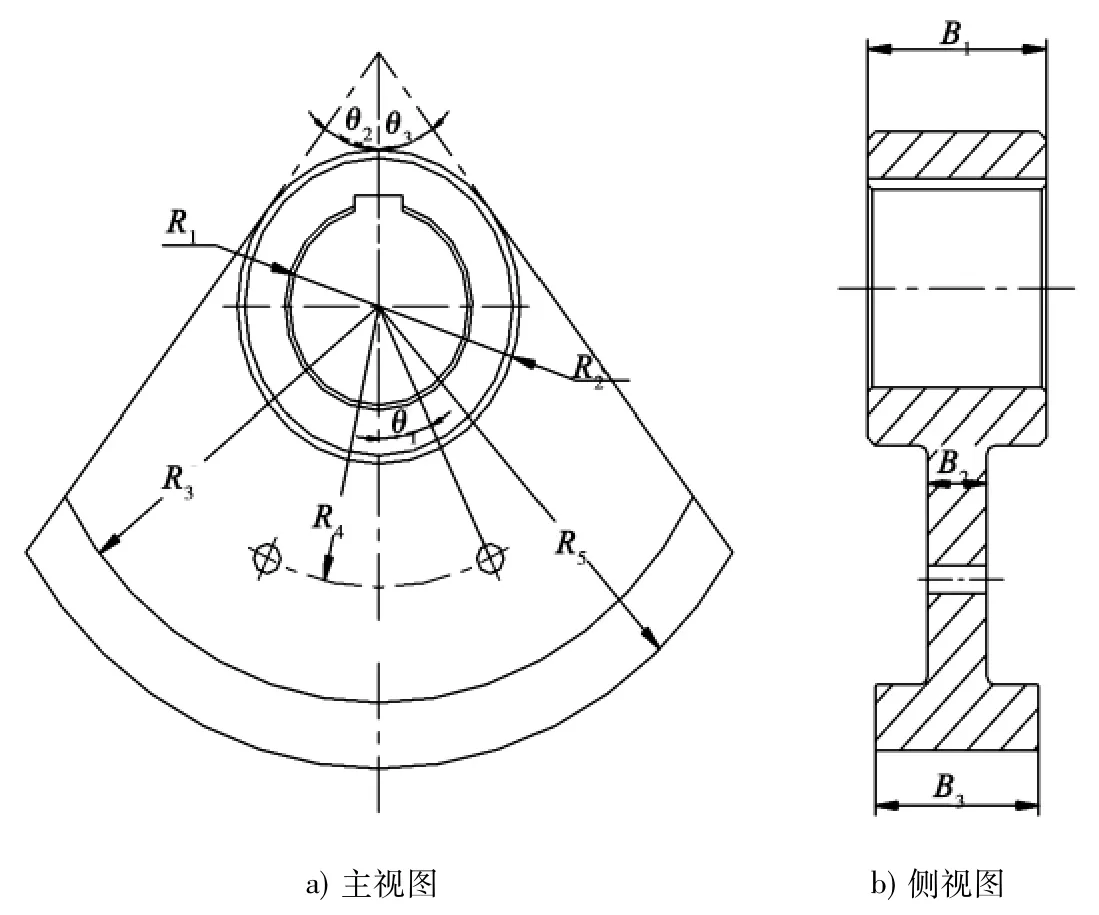
图2振动筛主偏心块结构示意图

1．3建立目标函数

目标函数是优化设计中预期要达到的目标，优化的目的就是在满足约束条件下找出目标函数的最优值。目标函数是设计变量的函数，常见的目标函数有体积、质量等［6］。

当振动筛启动时，激振频率由零逐渐增大，振幅也随之增大。当激振频率等于固有频率，振幅达到最大值，振动筛处于共振状态;继续增大激振频率时，振幅迅速下降。到启动后期，也就是当激振频率等于工作频率时，振动筛处于稳态振动，振幅基本不变［7］。

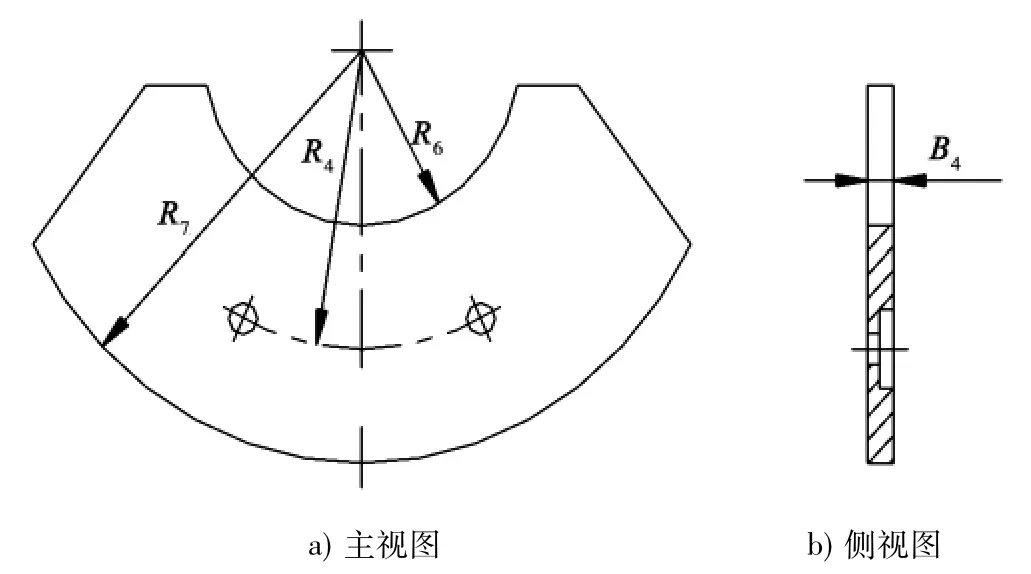
图3振动筛副偏心块结构示意图

多层直线振动筛的启动和停车是比较平稳且迅速的加速和减速过程，通过共振区的时间较短，在这两个过程中都不能出现明显的共振现象，否则将影响振动筛乃至整个沥青拌合站的安全性。

本次激振器优化的目标是尽量减小启动力矩，使振动筛能够实现稳定启动，保证整个振动筛的安全性。因而将激振器的启动力矩作为优化的目标函数，转动惯量J由激振器本身的结构决定，目标函数可以转化为使转动惯量J尽量小。

1．4建立约束函数

优化计算过程是在满足约束条件要求前提下反复改变设计变量使目标函数逼近最优值的过程。约束函数是优化设计过程中必须满足的一些设计条件，是根据设计对象应满足的功能要求而建立的约束条件［7－8］。激振器优化的目的是使启动力矩尽量小，同时还要保证振动筛的激振力基本保持不变以达到所需的振幅。若单纯地减小起振力矩，可能减小激振力，使得振幅达不到所需值。所以确定本次优化的约束条件为:激振力基本保持不变。在角速度一定的情况下，激振力仅与mr有关，所以最终的约束函数为保证mr基本不变，控制mr的变化量在2%以内。

1．5确定设计变量及其范围

在选取设计变量时应该考虑以下几点:所选择的设计变量要对目标函数有显著的影响;找出对目标函数影响较大的变量，尽可能减少设计变量的数量，提高计算效率。根据设计要求为设计变量选择合理的取值范围，取值范围过大会降低收敛速度，还可能出现假解的现象;取值范围过小则很可能将最优解排除在取值范围之外，从而无法得到最优解［7］。

由图2、3可知，该激振器结构涉及的尺寸参数较多，如主副偏心块不同部位的半径R1～R7、厚度B1～B4及角度θ1～θ3等。半径R1～R7由于装配和空间的限制，相互之间有联系和制约。

激振器的变量较多，每个变量对目标函数的影响程度不同，选取较优变量是本次优化的一个难点。同时该激振器结构复杂，建立目标函数、约束函数与设计变量之间的关系较为麻烦、工作繁琐、计算过程存在一定的误差，这是优化的第二个难点。另外设计变量之间复杂的关系对它们的取值范围以及约束条件影响很大，尤其是约束条件。约束条件对最终优化结果起着至关重要的作用，根据现有的条件很难确定设计变量之间的约束条件，这是本次优化的第三个难点。

基于上述工作遇到的种种难点，本次激振器结构的优化采用Pro/E软件。可以依据CAD图很精确的在Pro/E中绘制激振器的结构，建立激振器三维模型后其变量之间的关系相互约束，无需考虑它们之间复杂的约束条件。Pro/E软件内部具有分析测量功能，在给定密度时，可以从质量属性模块很容易地读取激振器的质量、质心位置、对质心的转动惯量等参数，减轻设计人员的劳动强度，计算结果相对精确［9－14］。

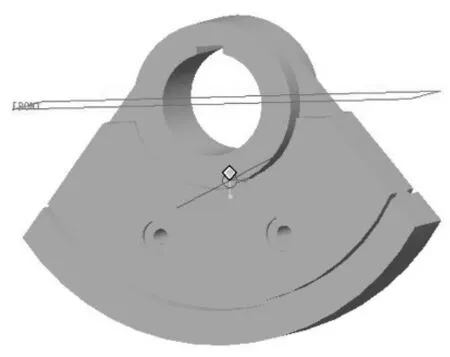
图4激振器优化前三维图

首先建立激振器的优化前三维模型如图4所示，优化前激振器相关参数如表1所示。从图4可以看出，现有激振器的键槽开在旋转轴所在front面的上侧，而上侧恰为结构的薄弱环节，对激振器的强度影响较大。为了改善激振器的受力状况，提高其承载能力，将键槽对称设计在front面的下侧，键槽改进图如图5所示。

表1激振器优化前的相关参数

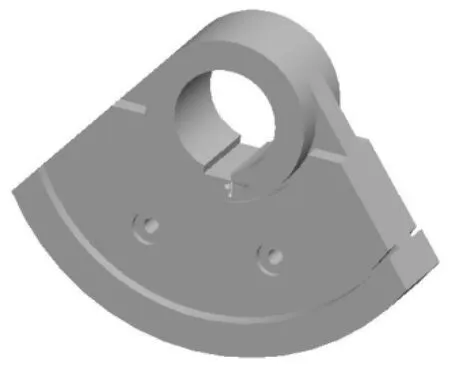
图5键槽改进图

表2设计变量及其取值范围

利用Pro/E中的敏感度分析来寻找较优设计变量及取值范围，原则为:在保证偏心块静偏心矩基本不变的条件下，尽量减小转动惯量。通过分析对比不同变量对目标函数和约束函数的影响程度选择较优设计变量，确定其取值范围如表2所示［9－15］( B4为两副偏心块的厚度和)。

1．6添加约束优化求解

设计变量及其取值范围确定之后，下一步添加约束对激振器进行优化。选取分析中的可行化/优化项目，选择研究类型为优化，求取转动惯量的最小值。激振器关于基准平面对称，由表1所示质心坐标仅和z有关，此时r=z。此时约束条件可以转化为m·z基本不变，含有m、z 2个参数，目标函数J=JC+mr2= JC+mz2中含有JC、m、z 3个参数，这3个参数可以在质量属性中直接读出。当上述6个设计变量变化时，JC、m、z都会随之变化。优化设计时选取JC最小，添加m、z的相关约束。在满足约束条件下，m、z有2种变化形式，即m增大z减小、m减小z增大。针对m、z这2种变化形式确定J=JC+mz2的最小值。根据激振器的原始数据及变化状态得出m、z对应的取值范围如表3所示。其中m·z的范围是9．550～9. 940。

针对表3的2种情况分别添加对应的约束条件，同时添加x=0这个约束条件，保证优化过程中激振器始终关于z轴对称。

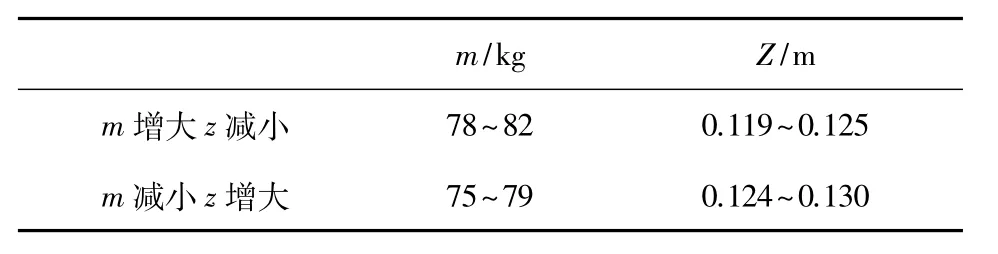
表3两种变化状态下m、z对应的取值范围

2优化结果

设置目标函数和约束条件，并添加设计变量的取值范围后，对激振器进行优化分析。2种状态下激

振器优化后相关参数如表4所示。

表4两种状态下优化后设计变量的取值

从表4可以看出，两组mr的变化量均在所要求的2%范围内。第二组对应的转动惯量J最小，因此选择第二组作为本次优化的结果。激振器优化后的结构图如图6所示。

为了便于实际的加工、生产，有必要对相关参数进行圆整，激振器

优化后及圆整后的相关参数如表5所示。

在原设计方案中，激振器的转动惯量为2．744 kg·m2，mr为9．770 kg·m。对比可知，优化后的激振器转动惯量仅为原设计方案的84. 80%，相比减小了15．20%，mr减少了0. 95%，基本保持不变，因此，优化效果显著。

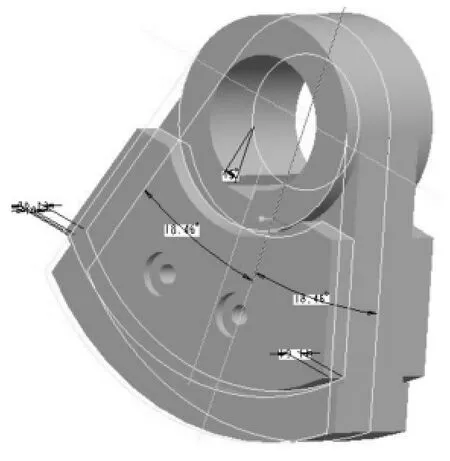
图6优化模型图

表5激振器优化后及圆整后的数据

3　结论

采用Pro/E软件对沥青搅拌设备用振动筛的激振器进行优化设计，通过对各几何结构参数的调节，使激振器在保持激振力大小基本不变的前提下，转动惯量减小15．20%。这有利于降低激振器的启动力矩，使振动筛起振平稳，从而提高振动筛的工作性能和使用寿命，应用价值较高。

参考文献:

［1］王永岩，张则荣．振动筛试验模型和原型相似试验研究［J］．机械工程学报，2011，47( 5) : 101－105．

［2］窦鹏．双激振器液控惯性振动筛起动过程研究［D］．郑州:郑州大学，2012．

［3］姬小娟．大型直线振动筛的动力学分析［D］．西安:西安科技大学，2013．

［4］王春彦，岳大鑫．振动筛振动电机的选取与激振力的调整［J］．农业装备与车辆工程，2007，45( 2) : 50－51．

［5］韩林山，武兰英，周林森，等．便携式防汛抢险打桩机激振器的优化设计［J］．水利电力机械，1999( 3) : 12－16．

［6］李增彬．基于虚拟样机技术的振动筛动力学分析及优化设计［D］．太原:太原理工大学，2010．

［7］张义民．机械振动［M］．北京:清华大学出版社，2007．

［8］周临震．激振系统的动态特性优化设计［D］．南京:南京航空航天大学，2004．

［9］易飚．Proe( MXD)运动仿真与机构运动分析实例［J］．苏州市职业大学学报，2004，15( 4) : 81－83．

［10］林清安．Pro/E零件设计基础［M］．北京:北京大学出版社，2000．

［11］黄圣杰，张益三，洪立群．Pro/ENGINEER2001高级开发实例［M］．北京:电子工业出版社，2002．

［12］黄圣杰．Pro/E高级开发实例［M］．北京:电子工业出版社，2002．

［13］林清安．Pro/ENGINEER2001零件设计［M］．北京:北京大学出版社，2000．

［14］林清安．野火4．0中文版工程图制作［M］．北京:电子工业出版社，2008．

［15］任晓良，张天军，范强，等．振动筛激振器的形状优化［J］．机械研究与应用，2003，16( 1) : 5－6．

(责任编辑:郭守真)

Optimization of Vibrating Screen Exciter

ZHANG Yushuang，YAN Chang，ZHANG Heng，LI Yao，XUE Xue，JIANG Wenzhi
( Key Laboratory for Highway Construction Technology and Equipment of Ministry of Education，Chang'an University，Xi'an 710064，China)

Abstract:According to the low starting torque characteristics when the vibrating screen works，the mathematical model of vibration exciter is set up in this paper．The sensitivity analysis of Pro/E software is used to find the optimal design variables and determine their scope，and add constraint conditions on the exciter to have the feasibility optimization．By adjusting the main geometric parameters of the exciter，the minimum value of the objective function and the corresponding design variable values are obtained．The results show that compared with the original model，the rotational inertia of vibrating screen of the exciter has decreased significantly，the static eccentricity is essentially the same，and the optimization effect is remarkable．

Key words:vibrating screen; vibration exciter; starting torque; mathematical model; sensitivity analysis; feasibility optimization; rotational inertia

作者简介:张玉双( 1989—)，女，河南驻马店人，硕士研究生，主要研究方向为工程机械设计及理论．

收稿日期:2015－04－20

DOI:10．3969/j．issn．1672－0032．2015．02．012

文章编号:1672－0032( 2015) 02－0062－05

文献标志码:A

中图分类号:U415．52