一维有限深方势阱中的束缚态*
2021-03-25陈晓云
陈晓云
(金陵科技学院理学院 江苏 南京 211169)
1 引言
一维有限深方势阱中粒子的运动性质,一直是量子力学中的基础问题[1~3].在所有量子力学教材中,如文献[1,2],都明确指出一维有限深对称方势阱中运动的粒子至少存在一个束缚态,且不需要满足任何条件,但是在文献[3]中,作者认为一维有限深对称方势阱中运动的粒子存在束缚态需要满足一定的条件,该结论与量子力学教材的结论存在矛盾.本文指出了文献[3]存在的问题,同时给出了一维对称、一维半壁有限深势阱中运动的粒子存在多个束缚态满足的条件.
2 一维有限深方势阱中束缚态能级的求解
2.1 对称方势阱
一维有限深方势阱示意图如图1所示.
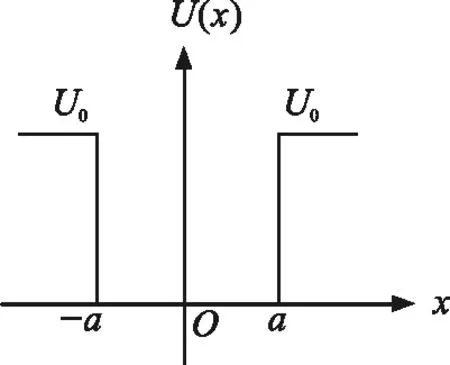
图1 一维有限深对称方势阱
考虑一个质量为m的粒子在一维有限深对称方势阱中的运动,对称方势阱可表示为
(1)
其中,2a为势阱的宽度,U0为势阱深度.
在势阱内(|x|≤a)和势阱外(|x|>a),薛定谔方程为
(2)
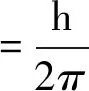
(3)
式(2)可化简为
(4)
其中k1,k2均为大于零的实数.方程(4)的通解为
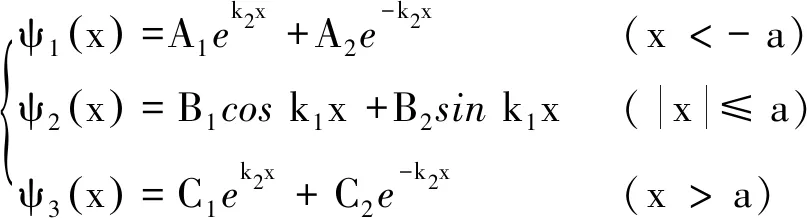
(5)
A1,A2,B1,B2,C1,C2为待定常数.
考虑束缚态条件|x|→时,ψ(x)→0,和波函数在x=±a处的连续性条件
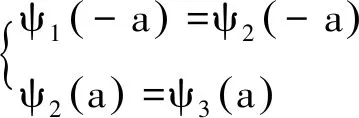
(6)
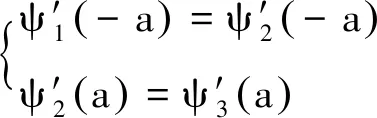
(7)
可得
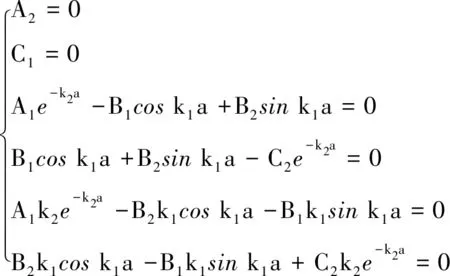
(8)
式(8)有非零解的充分必要条件是
(9)
化简得
(10)
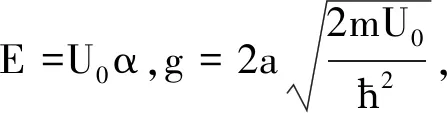
(11)
式中g为常量,且α,g的量纲均为1.对于束缚态,因为0 将1.1节中的U(x)换成下述式(12)的形式,就可以考虑一质量为m的粒子在一维半壁有限深方势阱中的运动 (12) 重复上述推导,可以得到能量E满足的超越方程为 (13) 下面利用Mathematica软件用图解法求解超越方程(11)与(13). 令 利用Mathematica的画图命令:Plot[f(α),{α,0,1}],可以得到函数f(α)的图形如图2所示. (a) (b) 图2给出了当g取不同数值时,函数f1(α)和f2(α)随着变量α(0<α<1)的变化曲线图.表1列出了对应于不同g值的对称势阱系统存在的束缚态能级. 表1 不同g值下一维有限深对称势阱存在的束缚态能级 从图2和表1,可以看到,随着g值的增加,曲线与α轴的交点数目增多,即束缚态能级的个数随之增加,并且存在如下规律: (1)对于对称势阱,当0 (2)通过细致调节g值的大小,可以得到如下规律: 对于对称势阱,当π 因此我们可以看到,对于对称势阱,不需要满足任何条件,当g取任意值时,即不管势阱的宽度、深度、粒子的质量取何值,粒子都会存在束缚态,且存在(n+1)个束缚态的条件为 nπ (14) 而对于半壁势阱,当且仅当g≥π时,才会有束缚态的出现,且运动粒子存在n个束缚态的条件为 (2n-1)π≤g<(2n+1)π (15) 我们的结论和量子力学教材是一致的,但是式(14)和文献[3]的结论存在矛盾,通过对文献[3]的推导过程仔细检查后发现,在文献[3]中,利用三角函数和角公式将式(8)变成式(9)时出现了错误.正确的推导过程如下: 文献[3]中,式(8)和本文中式(10)的定义一致 下面对该式进行化简. 则 定义 所以 sin (2k1a+φ)= sin 2k1acosφ+cos 2k1asinφ= 即式(10)可化简为 (16) sin (2k1a-φ)=sin 2k1acosφ-cos 2k1asinφ= 则式(10)可化简为 (17) 在本文中,我们只需用图解法直接求解方程(10),即可得到区间(0,U0)的束缚态能级,无需将势阱U0划分成两个区间,这样使得问题更简单更明了. 本文对一维有限深对称方势阱和半壁势阱中运动粒子的束缚能存在的条件进行了探究,计算结果表明,对于一维有限深对称方势阱,粒子束缚能的存在与势阱的宽度、深度和粒子的质量无关,肯定会有束缚态的存在;而在半壁势阱中,束缚态的出现是有条件的.这个条件可以用来解释原子分子物理中的现象,即两个粒子之间存在吸引不一定能够形成束缚态.因为我们在解两体问题的时候,引入雅可比坐标将两体问题化成单体问题时,在中心立场下,考虑基态情况,在球坐标系中,此时系统满足的薛定谔方程和一维半壁有限深势阱满足的方程一致.因此,即使这两个粒子之间存在吸引,也不一定能够形成束缚态.并且,分别给出了在两种势阱中运动的粒子存在n个束缚态的条件,指出了早期文献存在的问题.2.2 半壁有限深方势阱
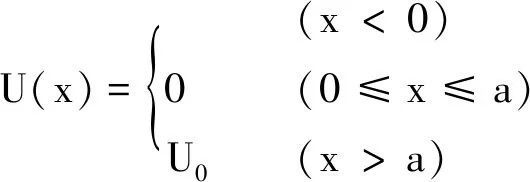
2.3 图解法求解超越方程
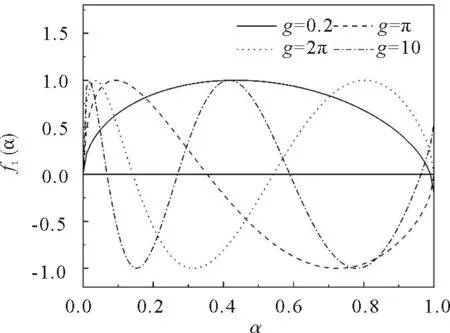
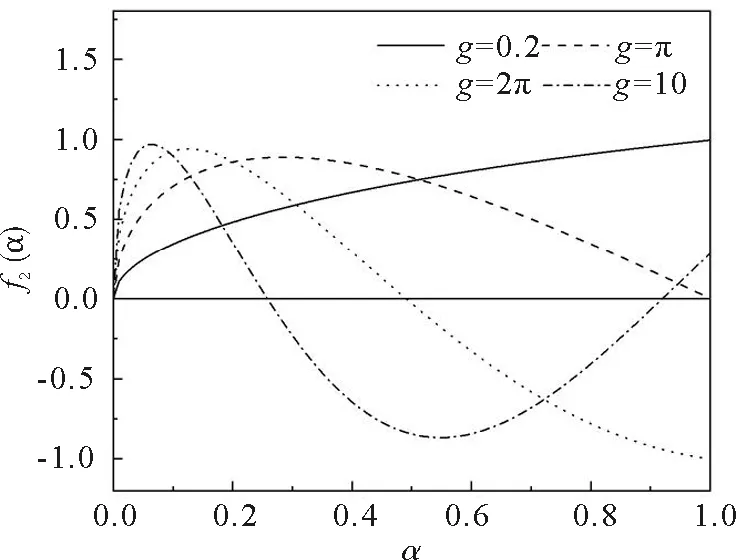

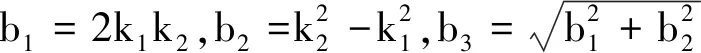
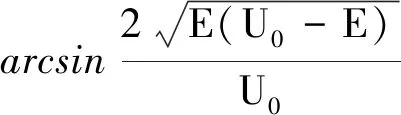
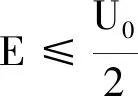
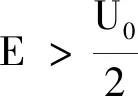
3 结束语
