利用PhET仿真软件对量子力学中有限深势阱的可视化教学实践*
2023-01-13杨玉平张曼曼胡周翔
杨玉平 张曼曼 孙 玮 胡周翔 刘 蓓 邹 斌
(中央民族大学理学院 北京 100081)
1 引言
无限深势阱是量子力学中最基本且重要的模型之一,对理解量子力学理论具有重要意义[1-2].但在很多低维量子受限系统(如纳米级金属薄膜、单层石墨烯、分子束外延生成的多层薄膜量子阱等)中,无限深势阱的理论结果总会有一定的偏差,而有限深势阱模型与实际量子体系更加吻合,并广泛适用.两者在求解定态薛定谔方程时,最大的区别是系统的边界条件不同,方程给出的能级结构和波函数形式也不同.但是,相较于多数经典量子力学教材[3-6]中详细讲解的一维无限深势阱模型,一维有限深势阱由于涉及颇为复杂的超越方程,在没有计算机辅助的情况下只能定性地讨论能级的取值范围和个数,无法精确地确定能级和具体的波函数.对于N个势阱情况,更是无法得出完整清晰的量子力学图像,是教师教学和学生学习的一个难点.将有限深势阱中微观粒子的量子化行为可视化,可以辅助教学,帮助学生理解相关抽象概念,解决实际系统中的复杂量子力学问题.
随着信息技术的进步、计算软件及网络的普及,涌现出多种虚拟仿真程序,以其逼真、准确、交互性强等特点,将信息技术与基础物理学科、专业物理实验等教学高度整合,为弥补传统理论教学和实践教学的不足提供了广阔的空间.其中,PhET互动仿真平台源于美国科罗拉多大学的物理教育科技(physics education technology,PhET)计划,其实验资源覆盖学科(包括物理、化学、生物、数学和信息等)广泛,且全球免费试用,提供简体中文版本,等等[7].在量子物理领域,PhET平台提供了电子衍射、黑体辐射、光电效应、量子波干涉、量子束缚态、量子隧穿与波包等实验,通过大量的图像显示、选择按钮和操作工具,可以帮助学生形象地理解科学概念,提高交互功能,增强学生的探究意识、自主学习和深度学习,提升教学质量与效能.2008年,文献[8-9]探讨了运用PhET仿真实验对玻尔模型、隧穿效应的有效教学及其教学效果;2015年,文献[10]运用PhET仿真实验模拟了量子波干涉、量子隧穿和波包.国内外学者教学效果的评估发现,学生对于PhET接受度很高.但要达成有效的教学目标,还需要教师精心去设计教学活动,以引导学生进行观察、测试、分析,并整合所学进行知识的建构.
本文结合一维有限深势阱的具体示例,依据PhET仿真软件提供的强大模拟功能,从求解微分方程、更新表达方式,通过图像式直观教学,拓展课程深度和广度,攻克知识难点和课程难点,获得正确的量子力学图景.并以此为基础,开展基于问题驱动的混合式课堂教学实践,以期在有限深势阱教学中提升学生的学习参与度,实现多元化教学目标.
2 一维有限深方势阱
2.1 定态薛定谔方程
考虑在一维空间中运动的粒子,其势能在一定区域内(x=-a到x=a)为零,而在此区域外,等于一个正数V0.求解定态薛定谔方程,利用系统的边界条件,得到束缚态能级E满足的超越方程为
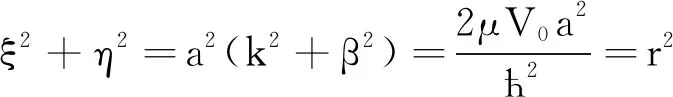
(1)
其中
ξ=ka
η=βa
波函数的解有两组,分别是奇宇称解和偶宇称解
(2)
(3)
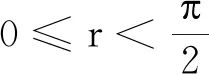

图1 图解法求解得到的束缚态能级
2.2 PhET虚拟仿真结果与分析
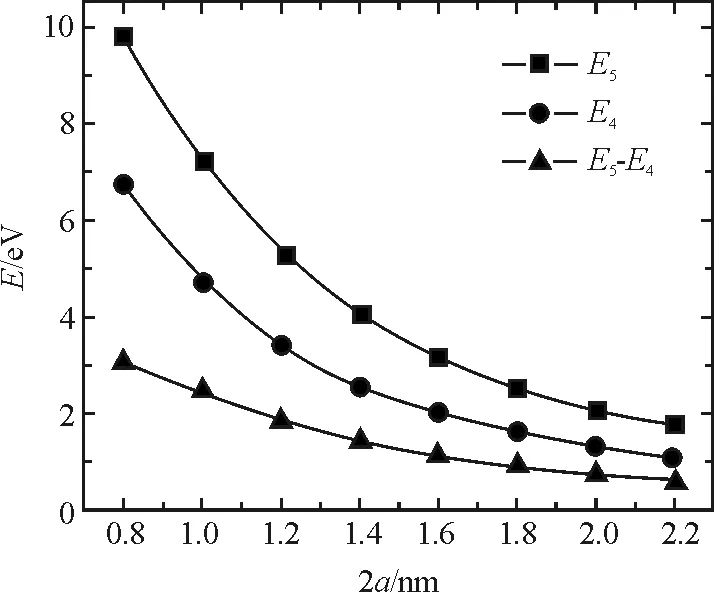
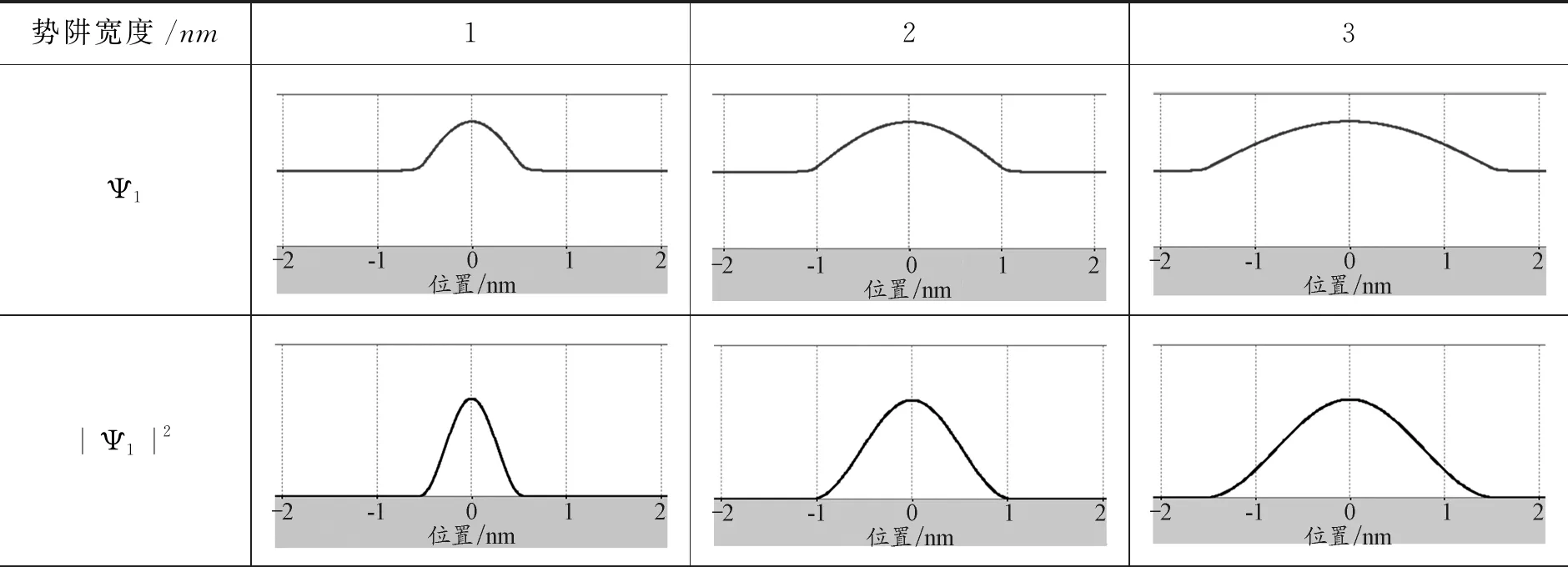
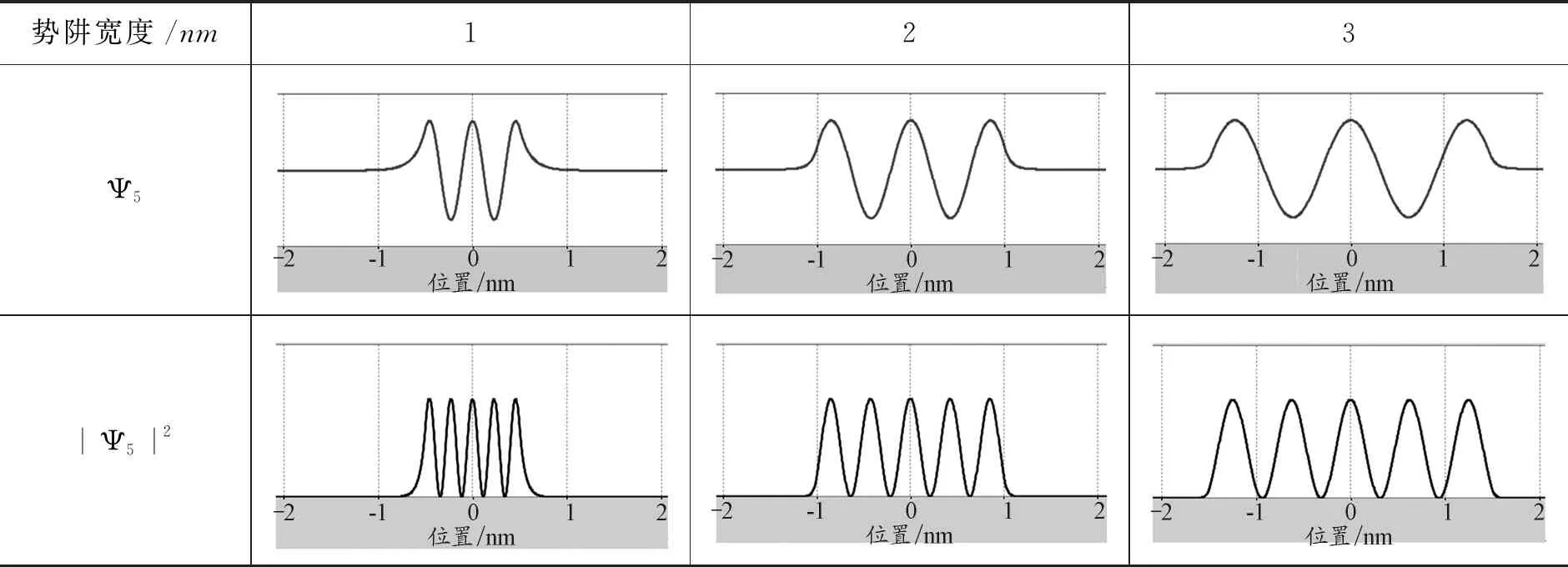
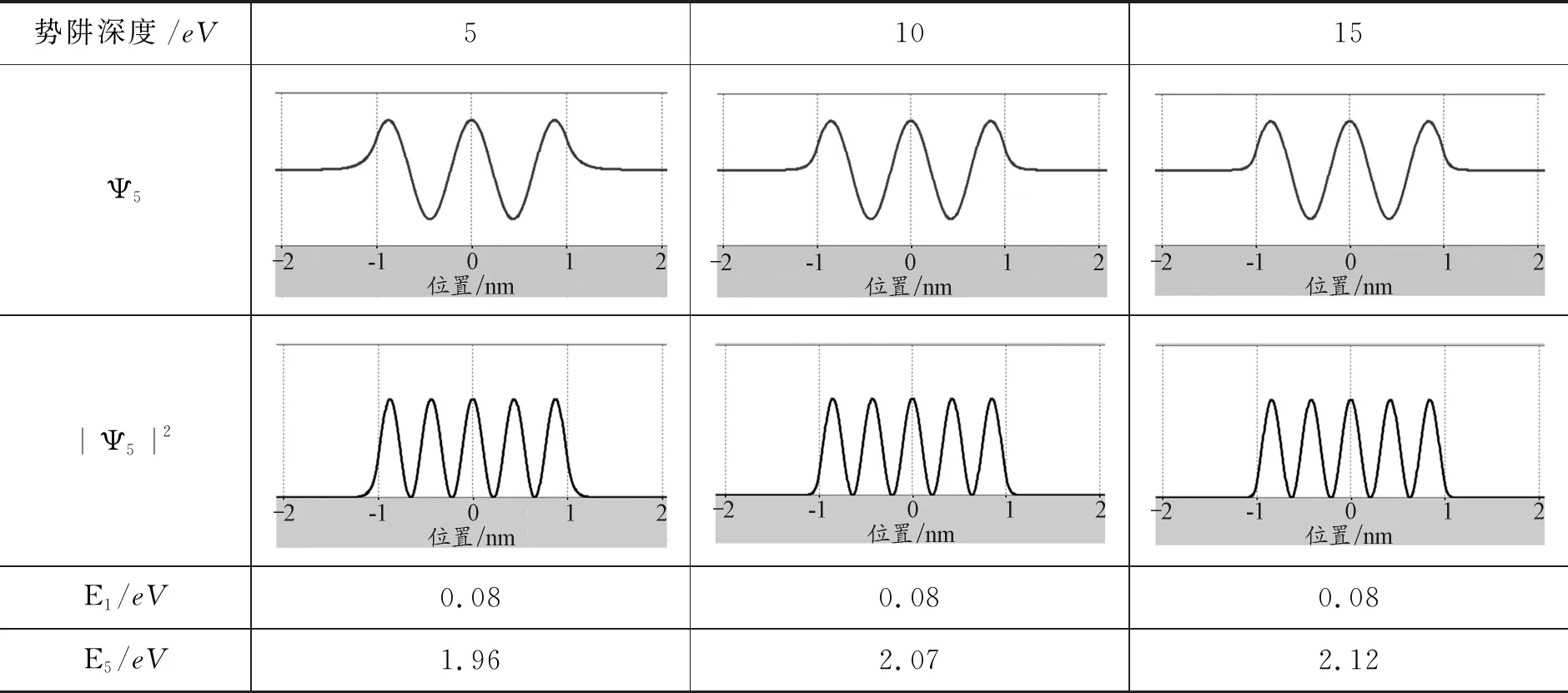
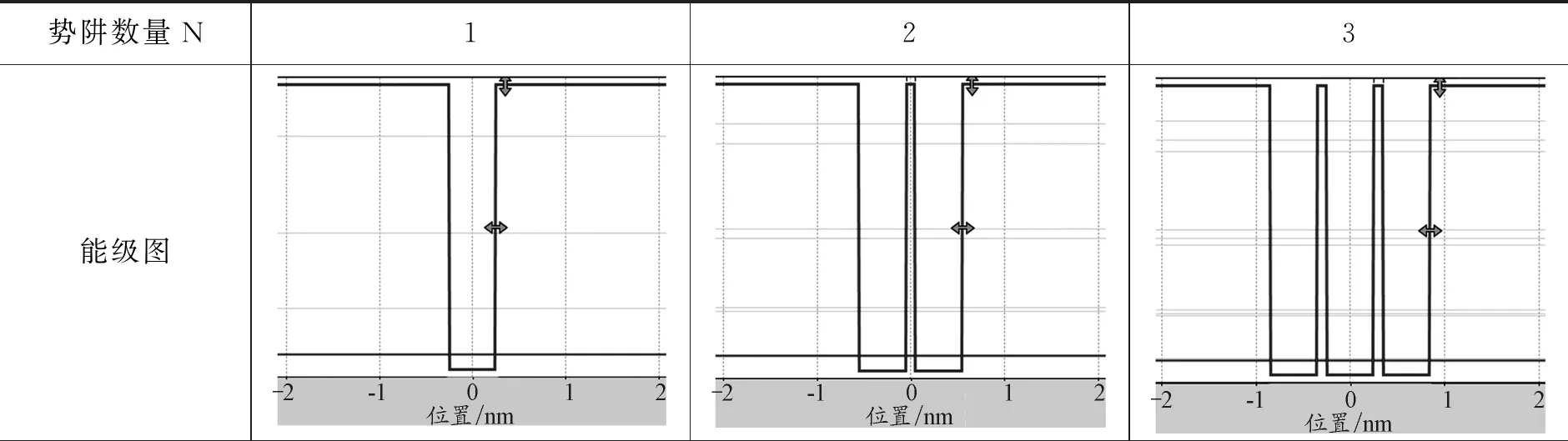
假设微观粒子为电子,质量为me=9.1×10-31kg,势阱的底部为零,势阱的深度V0=10 eV,势阱的宽度2a=2 nm,利用PhET仿真平台,计算得到的前3个本征态(束缚态)的能量本征值En、波函数Ψn和概率密度|Ψn|2的分布(包括势阱两侧的超越方程)如表1所示.当E 表1 前3个本征态的En、Ψn和|Ψn|2 保持势阱的深度(V0=10 eV)和粒子的质量(me)不变,改变方势阱的宽度(从0.8 nm增加到2.2 nm),能量E4、E5和两者的能量差如图2所示. 图2 En随势阱宽度的变化 可以发现,随着势阱宽度的增加,能量本征值随之减少,能级间能量差值也逐渐降低,体现出量子尺寸效应;发出光的频率减小,对应波长增大,即出现红移效应.同时,随着方势阱宽度的增加,能级数量逐渐增多. 不同势阱宽度情况下波函数Ψn和概率密度|Ψn|2的分布如表2所示.随着方势阱宽度的增加,Ψn和|Ψn|2的宽度也随之增加,且始终比方势阱宽度略宽,说明势阱外仍有概率分布;在确定宽度下,高能级概率分布跃出势阱的比低能级概率分布跃出势阱的要多.从式(1)来看:当|x|≥a时,波函数是呈指数衰减的形式,即Ψ(x)=Be-β|x|;高能级对应的β取值较小,衰减得要慢一些. 表2 Ψn和|Ψn|2随势阱宽度的变化 续表2 保持势阱的宽度(2a=2 nm)不变,改变方势阱的深度(从5 eV增加到15 eV),电子的质量设为me,第5个本征态的E5、Ψ5和|Ψ5|2如表3所示.随着势阱深度的增加,能级的数量不断增加.由式(1)可知V0的增加会引起r的增加,通过图解法求解结果来看r越大对应能级数越多;此外,随着势阱深度的增加,每一能级对应能量值呈上升趋势,但是存在极限值(无限深势阱的束缚态能级En).Ψn和|Ψn|2的宽度逐渐减小,但始终比无限深方势阱宽度略宽.在确定宽度下,第5个本征态的概率分布跃出势阱的比例随势阱深度的增加而减小;在无限深的情况下,势阱外和阱壁处粒子(电子)存在的概率为零.从式(1)来看:当|x|≥a时,波函数是呈指数衰减的形式,即Ψ(x)=Be-β|x|;增加势阱深度V0使得β值增大,衰减得要快一些. 表3 E5、Ψ5和|Ψ5|2随势阱高度的变化 保持势阱的宽度(2a=2 nm)和深度(10 eV)不变,改变方势阱中粒子(电子)的有效质量μ,第5个本征态的E5(加粗能级)、Ψ5和|Ψ5|2如表4所示.随着粒子质量的增加,能级的数量不断增加.由式(1)可知粒子有效质量μ的增加会引起r的增加,通过图解法求解结果来看r越大对应能级数越多.此外,随着粒子质量的增加,每一能级对应能量值呈下降趋势;Ψn和|Ψn|2的宽度略有减小,但始终比方势阱宽度略宽.在确定势阱宽度和深度下,第5个本征态的概率分布跃出势阱的比例随粒子有效质量μ的增加而减小;从式(1)来看,当|x|≥a时,波函数是呈指数衰减的形式,即Ψ(x)=Be-β|x|;增加粒子有效质量μ使得β值增大,衰减得要更快. 表4 En、Ψ5和|Ψ5|2随粒子质量的变化 对于N个有限深势阱中微观粒子的束缚态能级和波函数,可以从定态薛定谔方程出发,由波函数标准条件导出波函数中待定系数满足的(4N-2)元线性方程组.由线性方程组系数行列式等于零的超越方程计算出微观粒子的能级,通过计算线性方程组的基础解系求得束缚定态波函数[12].每增加1个势阱,定态波函数的求解区间增加2个:波函数增加两端,确定能级的齐次线性方程组增加4个未知量[13]. 假设微观粒子为电子,质量为me=9.1×10-31kg,势阱的底部为零,势阱的深度V0=20 eV,势阱的宽度2a=0.5 nm,而中间势垒宽度d=0.1 nm,利用PhET仿真平台,计算得到的单个势阱到3个势阱的电子能级图如表5所示.与单势阱相比,双势阱的能级都是两两成对出现的,而三势阱的能级都是三三出现的.以n=4的能级为例,单势阱的能量值为16.33 eV,双势阱的能量值分别为15.82 eV和17.18 eV,三势阱的能量值分别为15.45 eV,16.25 eV和17.56 eV,四势阱的能量值分别为15.41 eV,15.91 eV,16.84 eV和17.81 eV. 表5 多个势阱的能级En 续表5 图3绘制了1~5个对称势阱的能级图. 图3 En随势阱数量的变化 可以看出,随着N的增加,原来的单势阱能级被分裂为N条,其中最小的能级低于原能级,最高的能级高于原能级;且随着N的增加,能级分裂的宽度逐渐增大.值得注意的是,原来的一个能级分裂成为的N条新能级并不是等间隔的;当量子阱数目N越大,能级间隙越小;随着量子阱数目N的进一步增加,最终可形成能带. 当N=5时,保持势阱的宽度(2a=0.5 nm)和高度(20 eV)不变,改变中间势垒的宽度d,前4个本征态的能级图和En的数值如表6所示.随着势垒宽度的增加,能级分裂的条数不变,但是能级分裂的间隔越来越小.以n=4为例,E4能级在d分别为0.05 nm,0.10 nm和0.20 nm时,对应的最高能级和最低能级差分别为4.54 eV,2.50 eV和0.86 eV.随着中间势垒宽度的进一步增加,最终能级分裂现象消失,能级分布与单势阱的相同. 表6 概率随中间势垒宽度d的变化 无论是单势阱还是多势阱问题,定态的波函数都是以势阱中心(x=0)为对称轴的奇偶函数.其中,基态为偶函数,随着能级的升高,定态波函数的奇偶性轮流呈现.限于篇幅,本文只给出单势阱至三势阱的前几个本征态的概率密度|Ψn|2的图形,如表7所示.与一维单势阱相比,双势阱前6个本征态的|Ψn|2分别对应单势阱的前3个本征态;成对能级对应的概率密度|Ψn|2相似,存在峰位的数量相同,主要差别在于中央波谷处幅度高低不同;双势阱的|Ψn|2关于中心(x=0)对称分布,随着能级增加,每一组简并能级比上一组简并能级增加2个峰位.此外与单势阱|Ψn|2类似,势阱宽度越大,每个能级 |Ψn|2的峰变宽;势阱深度越高,每个能级|Ψn|2的峰变得更尖锐,峰宽变窄(表7未给出). 表7 |Ψn|2随势阱个数N的变化 与一维单势阱相比,三势阱前9个本征态对应的|Ψn|2分别对应单势阱的前3个本征态.与双势阱有所不同的是,三重能级中最高能级和最低能级对应的概率密度|Ψn|2相似,存在峰位的数量相同,主要差别在于中央波峰(或波谷)处幅度高低不同;但是,中间能级的峰位数量和中央波峰(或波谷)处幅度高低与最高能级和最低能级存在显著不同.此外,不同三势阱的|Ψn|2也是关于中心(x=0)对称分布,随着能级增加,每一组简并能级比上一组简并能级增加3个峰位.此外,与单势阱|Ψn|2类似,势阱宽度越大,每个能级 |Ψn|2的峰变宽;势阱深度越高,每个能级|Ψn|2的峰变得更尖锐,峰宽变窄. 采用线上线下混合式、翻转课堂的教学形式开展线上预习、虚拟仿真实验和课堂展示,在增加学生线上线下课堂参与度的同时增加学生对教学内容的思考,实现有效学习. 课前预习环节,教师给出本节课的学习重难点以及注意事项,学生根据教师给出的学习单进行线上视频学习和虚拟仿真,以小组学习的方式,每位学生负责相应的任务点,准备在翻转课堂上,以“教师”的角色进行备课和内容讲授.本节给出的学习单提纲如下: (1)有限深单势阱 1)给出前3个本征态(束缚态)的能量本征值En、波函数Ψn和概率密度|Ψn|2的分布(包括势阱两侧的超越方程),验证课上的理论推导结果. 2)改变方势阱的宽度,并描述En的变化(最好定量),解释量子尺寸效应. 3)改变方势阱的宽度,并描述Ψn和|Ψn|2的变化,解释这些变化. 4)改变方势阱的深度,并描述En、Ψn和|Ψn|2的变化,解释这些变化. 5)改变粒子的质量,并描述En、Ψn和|Ψn|2的变化,解释这些变化. 6)保持方势阱的深度(V0)不变,当阱内的势能U(x)分别大于、等于或小于零时,其En、Ψn和|Ψn|2的变化有哪些?解释这些变化. (2)有限深多势阱 1)与一维单势阱相比,描述束缚态的能级(En)结构发生了哪些变化? 2)与一维单势阱相比,描述束缚态的Ψn和|Ψn|2发生了哪些变化? 3)改变宽度和深度,束缚态的能量本征值(En)发生了哪些变化? 4)改变宽度和深度,束缚态下Ψn和|Ψn|2发生了哪些变化. 以问题为导向的小组学习更能激发学生对实验的兴趣,以更开放、更灵活的方式强化学生对量子物理有限深势阱问题的探究与思考,增加学生对于教学内容的思考量. 教学过程中,学生是学习的主体,教师更多地扮演一个“主持人”的角色.学生根据自己的备课内容,结合PPT对授课内容进行详细的讲解.PhET虚拟仿真平台把抽象的科学概念(能级、能带)和不可见的微观事实(如波函数、概率)可视化,同时提供了增强理解的动态化模型;学生在授课过程中可以现场演示并解释实验结果,体验直观、逼真的实验过程;也可以基于查阅的文献,结合微分方程的求解结果进行分析.教师的职责主要是对学生讲解过程中漏掉的内容进行补充,对学生讲不透的内容进行解析,对需要重点理解和需要拓展的知识点进行强调,以及最后答学生问.最终达到抽象与形象、理论与实验相结合的目的. 在课后教师鼓励学生跨组交流,查阅文献,进一步完善小组任务;最终,以小组为单位提交一篇研究报告.总之,基于学习单预习、虚拟仿真、小组讨论、翻转课堂、教师讲授、提交报告等形式,有效提高了学生的参与度和课堂教学质量. 本文借助PhET虚拟仿真平台,对一维有限深势阱问题进行了可视化研究,并将一维有限深方势阱结论拓展到多势阱情况,强调了量子力学教学中有限深势阱问题的重要意义.通过图形和视频,形象地给出了一维有限深势阱的能级结构和粒子在阱内的概率分布,使得学生能够直观理解能量量子化的形成以及延伸出对一维光子晶体、超晶格、固体能带复杂量子力学体系的理解,从而为学习和应用量子理论体系建立一个牢固可靠的认知基础.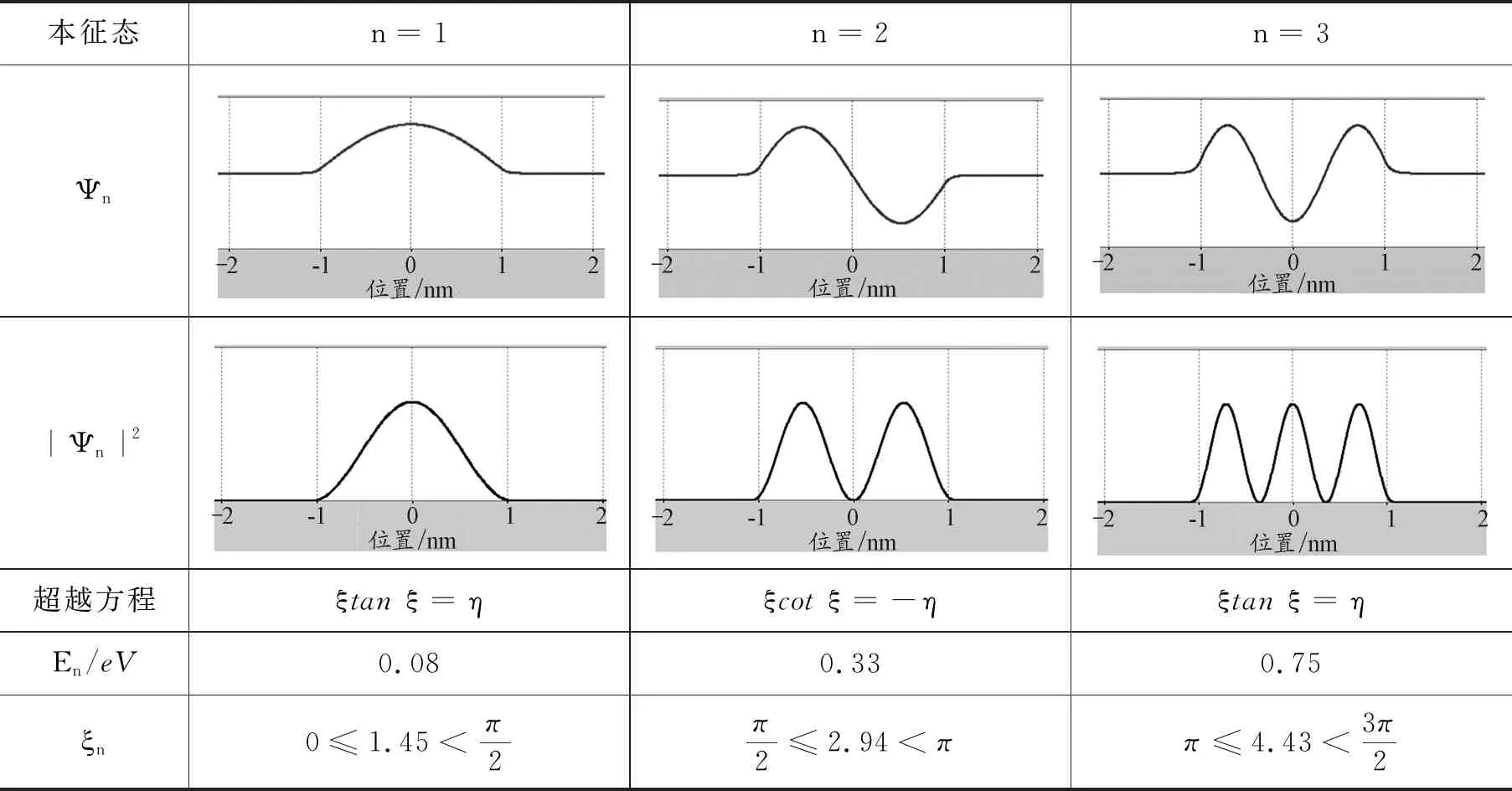

3 有限深多势阱
3.1 有限深多势阱的能级
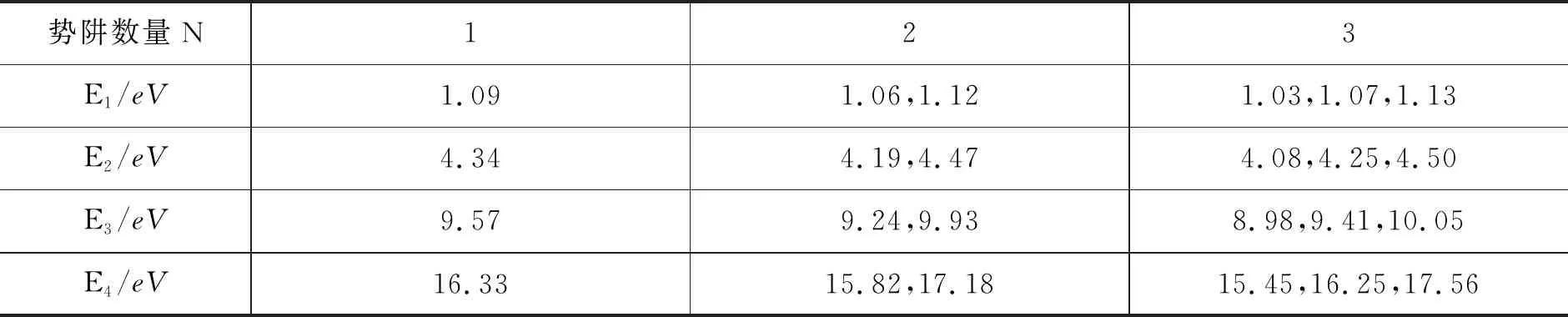

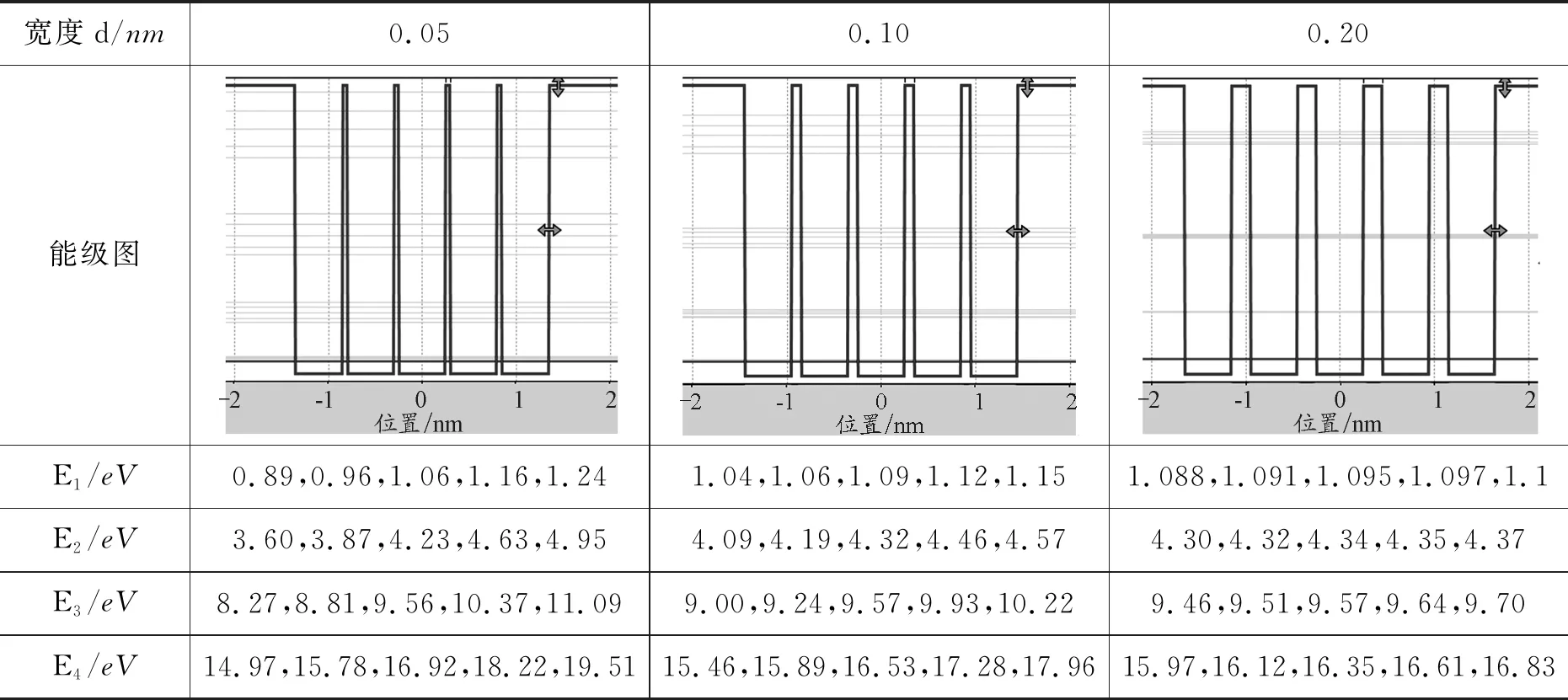
3.2 有限深多势阱本征态下的概率分布

4 教学过程
4.1 课前预习
4.2 翻转课堂
4.3 课后
5 结论
