有关变压器空载电流问题的探究

2016-01-12郑金

物理通报 2015年6期

关键词：原线圈副线圈自感

有关变压器空载电流问题的探究

郑金

(凌源市职教中心辽宁朝阳122500)

摘要：用多种方法定量推导了变压器空载电流的解析式、有效值、电功率以及空载电流与磁通量的关系、空载电流与原线圈中电流的关系.

关键词：变压器空载电流自感电动势磁通量

收稿日期：(2014-11-03)

在对变压器的教学过程中，有关空载电流的问题是难点，常产生一些疑问，如变压器空载时，即副线圈开路时，原线圈中是否有电流？究竟为多大？如何变化，由哪些因素决定？有何特点？下面从5个方面进行分析.

1空载电流的解析式

对于变压器空载时原线圈中的电流解析式，有多种推导方法.

方法1:利用部分电路欧姆定律

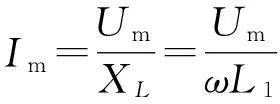
或者根据纯电感电路中电流、电压的瞬时值函数是互余关系，得

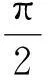
方法2:利用自感电动势和微积分知识

由于理想变压器的原线圈没有电阻，则有u1=

两边积分得

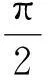
该结果是错误的，因为在纯电感电路中，虽然电流、电压的有效值之间遵循欧姆定律，但电流、电压的瞬时值之间却不遵循欧姆定律，因此初始条件中的电流关系式不成立.

方法3:利用变压器线圈自感和互感理论

理想变压器的结构示意图如图1所示.当原、副线圈中的电流都为正方向时磁通量方向一致，而自感电动势总是阻碍线圈中电流的变化，即感应电动势与电流变化的方向相反，则原线圈中的感应电动势为

由于线圈没有电阻，则uab=-eab，udc=-edc，因此

(1)

同理

图1

由于理想变压器没有漏磁，则

可得互感系数为

(2)

设u1=U1cosωt，则

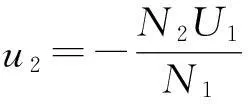
输出电路为纯电阻电路，则由欧姆定律得

(3)

设

i1=I1cos(ωt+θ)

(4)

将式(3)、(4)及u1关系式代入式(1)，化简得

由辅助角公式可知

由等式两边对应项系数相等可得

因此原线圈中的电流为

i1=I1cos(ωt-φ)=I1cosφcosωt+I1sinφsinωt

所以

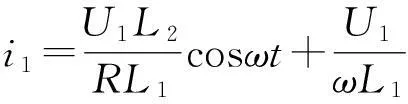
电压最大值为U1=Um，当R→时，即副线圈空载时，原线圈中的电流即空载电流为

可知当副线圈接上负载时，原线圈增加的电流为

该电流与副线圈的电流之比跟线圈匝数成反比，且与电压之间的相位差为零，因此是有功电流.

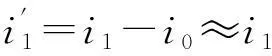
【例题】一个理想变压器匝数比为10∶1，原线圈接正弦交流电压u1=Umsinωt，其中Um=311 V,ω=100π s-1,副线圈开路，当原线圈中电流的瞬时值为零时，副线圈两端电压的瞬时值为多少？

2空载电流的有效值

或者从自感电动势角度而言，如果L1→，则自感电动势与输入电压的大小相等，方向相反，即u1=-e1，因此电路中I0→0.

但实际上，由于有漏磁通，而且线圈存在很小的电阻，使自感电动势略小于电源电压，二者不能完全相互抵消，因此原线圈回路中有很小的电流，称为空载电流，也叫磁化电流，是反映变压器的一个参量，其值越小越好，一般为初级额定电流的3%～8%，如果大于此值，表明初级线圈匝数绕少了(电感不够)，或者是铁芯结合处距离太大，或者是铁芯的磁导率太小.若发现磁化电流太大，则变压器不能使用.

3空载电流的电功率

空载电流的瞬时功率为