正弦波传播介质中的质点在做简谐运动吗——对人教版《物理·选修3-4》波动部分的一点看法

正弦波传播介质中的质点在做简谐运动吗
——对人教版《物理·选修3-4》波动部分的一点看法

张建斌柴春琪

(嘉兴市第一中学浙江 嘉兴314050)

摘 要：人民教育出版社2010年4月第3版《物理·选修3-4》认为,有正弦波传播的介质中的质点在做简谐运动.但笔者查阅了相关书籍后发现这一说法欠妥.本文将从平面简谐波的波动方程和介质波的能量出发，分析机械波能量在空间上的分布、随时间的变化与能量传递的实质，通过与简谐运动进行对比，对新教材中关于机械波传播过程中介质中质点的运动作新的描述,即“简谐波是简谐运动在介质中的传播，介质中各质点做的是运动规律满足正弦(或余弦)图像的受迫振动”.

关键词：受迫振动简谐运动机械波能量传递

收稿日期：(2014-05-08)

普通高中课程标准实验教科书《物理·选修3-4》(人民教育出版社2010年4月第3版)第27页有这样一句话，“介质中有正弦波传播时，介质的质点在做简谐运动”.但简谐运动的能量在整个振动过程中是一个守恒量，简谐运动的过程是动能和势能相互转化的过程，这样做简谐运动的介质中质点将无法实现传递能量的功能.本文主要阐述机械波的能量及其传递，并尝试对新教材中关于机械波传播过程中介质中质点的运动谈一点自己的看法.

1平面简谐波的波动方程

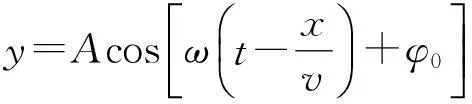
(1)

这就是平面简谐波方程，它可以描述平面简谐波在传播方向上任意点的振动规律.

2介质中波的能量分布

一列波在弹性介质中传播时，各体元都在平衡位置附近振动，所以具有动能，同时，各体元发生形变，又有弹性势能.现以简谐横波为例，研究某体元的动能、势能和总能量的变化规律.

2.1动能

在有简谐横波传播的介质中，取一微元，根据平面简谐波方程可得到其振动速度

设介质密度为ρ，微元体积为dV，则该体元的动能为

2.2形变势能

我们选取的介质中的微元同时受到相邻的微元的作用而发生剪切形变(即在力偶作用下，两平行截面发生相对移动的形变)，如图1所示.

图1

对于传播横波的介质中的微元而言，其剪切形变简化为如图2所示，有

所以选取的微元的形变势能为

图2

2.3总能量

弹性介质中横波的波动方程可写为

对式(1)偏导运算可得

即波动中某一微元的动能和势能具有相同的数值，它们同时达到最大和最小.微元的总能量等于两者之和，即

实际中，常用能量密度

也是时间和空间坐标的函数，体现出波的能量在时间和空间上的周期性.

3机械波能量及其传递的高中教学

基于高中学生的数学基础，我们在进行这部分内容教学时，应切合学生实际，从学生已有知识基础和能力水平去构建新的知识体系.笔者在实际辅导教学中先让学生回顾弹簧拉伸形变和形变势能，然后简单介绍剪切形变和剪切形变势能.接着如下过程.

3.1机械波能量在空间上的分布

机械波在传播过程中，某时刻介质中某处质点的动能决定于该处质点的振动速度的大小，而势能决定于该处介质的形变(即剪切形变)大小.

图3所示为一列沿弹性绳传播的简谐横波，分别在位于平衡位置的B和位于最大位移的A,C处，取相同长度Δx(Δx→0)的媒质微元来讨论.

图3

可以看出B处质点的振动速度最大，同时该处绳子的形变也最大，因此该处质点的动能和势能为最大，其总能量也就最大.而对于A,C两处的质点，此时它们的振动速度为零，且该处绳子的形变也趋于零，因此该处质点的动能和势能都为零，即总能量也就最小(为零)，而A与B之间,B与C之间的质点的能量就介于最大和零之间.可见，同一时刻介质中各处的能量分布并不相同，在波峰和波谷处质点的能量最小(为零)，而在平衡位置处质点的能量最大.质点离平衡位置越近，能量就越大，即能量在波的传播方向上呈现周期性的分布，随着波形的向前传播，这种能量分布的状态也以波的传播速度向前传递.

3.2机械波能量随时间的变化

弹簧振子和单摆做自由的简谐运动时，只有振动系统内部的动能和势能的转化，系统的总能量是守恒的，这表明振动系统不与外界交换能量，可认为是一个“保守系统”.在简谐波的传播过程中，每一质点的运动规律与简谐运动相同，那么每一质点的能量是否也守恒呢?

图4

3.3机械波能量传递的实质

如图5所示为一列沿绳子向右传播的简谐横波在某一时刻的波形图.A,B,C为绳子上3个相邻的质点，设波是由A传向B，再传向C的，则B质点的振动是由于A质点的振动使绳子发生形变而产生的弹力F带动的，这个弹力对A做负功而对B做正功，使A质点不断释放能量，而使B质点不断吸收能量，使能量从A传递给B.同理,B质点又不断地向C质点传递能量.但每一质点在任一小段时间Δt(Δt→0)内，从前一质点吸收的能量并不等于向后一质点释放的能量，如图5中的质点B，由于两侧介质的形变大小不同，两侧质点A,C对它的弹力也就不同，左侧形变小,弹力小，右侧形变大,弹力大，因此在这一时刻附近的一小段时间Δt(Δt→0)内A对B做的正功小于B克服C做的功，也就是说B从A吸收的能量小于B向C释放的能量.因而B向上离开平衡位置的过程中总能量是减少的.同理，在B返回平衡位置的过程中总能量又是增加的.这样通过介质之间的相互作用力做功，使每一质点周期性地积累能量和释放能量，实现了能量随波的传递.

图5

综上，机械波在传播过程中，每一时刻介质中各处的能量(即能量密度)在波的传播方向上呈现周期性分布，是不均匀的，而每一质点的能量也是随时间周期性变化的，是不守恒的，能量的传递是通过质点之间的相互作用力做功来实现的.

4对教材中 “波动”部分的一点看法

4.1关于简谐运动

质点在某位置所受的力(沿运动方向受的力)为零，则此位置称为平衡位置.若作用于质点的力总与质点相对平衡位置的位移(线位移或角位移)成正比，且指向平衡位置，则此作用力称为线性回复力.以平衡位置为原点，以x表示质点相对于原点的位移，线性回复力fx=-κx，κ是正常量.力fx是质点位移x的线性函数，且与位移x反向，即促使质点返回平衡位置.质点在线性回复力作用下围绕平衡位置的运动叫做简谐运动.

x=Acos(ω0t+α)=Asin(ω0t+α′)

这就是简谐运动的运动学方程，其运动图像为余弦(或正弦)图线.

教材对简谐运动的定义，“如果质点的位移与时间的关系遵从正弦函数的规律，即它的振动图像(x-t图)是一条正弦曲线，这样的振动叫做简谐运动”，这个定义显然不够.教材既然通过振动图像来定义简谐运动，则必须同时应说明图像x=Asin(ω0t+α′)中的ω0是由振动系统本身的性质决定的.这样也有助于学生区分简谐运动与有简谐波传播的介质中质点的运动.