对一道典型运动学例题错解剖析

对一道典型运动学例题错解剖析

陈向群 孟凡玲

(马鞍山市第二中学安徽 马鞍山243000) (阜阳市第二中学安徽 阜阳236033)

摘 要：通过对一道典型运动学例题错解剖析，进一步分析了在解答问题过程中思维偏差产生的根源以及应对的教学策略.对帮助学生进一步认清杆在圆柱体或球上的运动过程和物理图景，突破思维的难点，扫清学习中的障碍以及对帮助学生从本质上把握物理规律和解决物理问题，将起到积极的促进作用.

关键词：运动学合成与分解 错解分析物理图景

收稿日期：(2014-07-29)

笔者在各种自主招生和竞赛的教辅资料中常看到这样一道典型运动学例题，但无一例外，解答都是错误的.

图1

【例题】如图1所示，AB杆的A端以匀速v在水平地面上运动，运动时杆始终与一半圆柱体相切.半圆柱体的半径为R.当杆与水平线的交角为θ时，求杆的角速度ω及杆上与半圆柱体相切点C的速度及杆与半圆柱接触点C′的速度大小.

错解:由于半圆柱体静止，杆上C点的速度的法向分量为零，故杆上C点速度必沿杆，以C点为基点，将杆上A点速度v分解为沿杆方向的分量v1和

垂直于杆方向的分量v2，如图2所示.

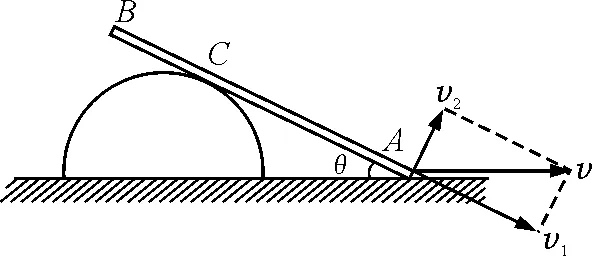
图2

则v1是A点与杆上C点相同的沿杆方向平动的速度，v2是A点对C点转动速度，故杆上C点速度为

vC=v1=vcosθ

(1)

又

v2=vsinθ=ω·AC

而

AC=Rcotθ

故

如图3所示，由于杆与圆柱的接触点C′沿圆周运动，杆转过的角度与半径转过的角度相同，所以杆转动的角速度与C′点沿圆柱体转动的角速度相同,所以C′点的速度为

vC′=ωR=vtanθsinθ

(2)

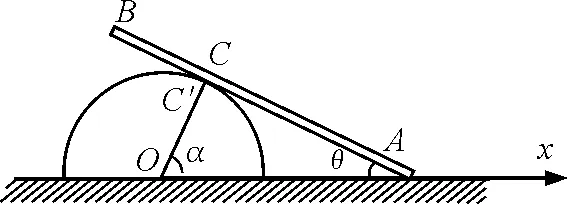
图3

粗看起来，我们很难发现错在哪里，有一定的隐蔽性，到底哪里出了问题？

正解:结合图3，以圆柱体横截面的圆心O为坐标原点,沿地面上杆A点的速度方向建立x轴，A点的坐标为x.则

对x求导

(3)

由于

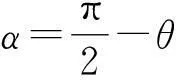
(4)

联立式(3)，(4)，则有C′点沿圆柱体转动的角速度为

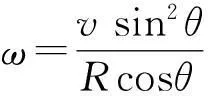
(5)

所以C′点的速度为

vC′=ωR=vtanθsinθ

(6)

式(2)与式(6)相同，此解与上面的解法不同，但结论相同，没有发现错误.

由于杆上C点的速度是接触点C点相对于杆的端点A点的速度，故以A点为坐标原点，沿杆AB的方向建立x轴，如图4所示.

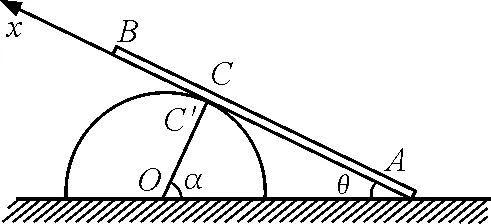
图4

C点的坐标为x.则

(7)

将式(5)代入式(7)，得到

(8)

式(8)与式(1)明显不同，造成原因是我们只考虑杆在圆柱体上的平动导致的杆上C点的移动，没有把杆在圆柱体上的转动所导致的杆上C点的移动考虑进来！

如图5所示，杆在圆柱体上发生无滑动的纯转动，杆由①位置转动到②位置的过程中，杆上C点同时也发生了移动.由于杆在圆柱体上没有滑动， 故杆上C点移动的速度与圆柱体上C′点移动速度始终大小相等.

图5

所以杆上的C点实际的速度是由两个速度叠加而成的，则有

以上对错因的剖析，使我们认识到物理图景是把物体的运动和相互作用生动形象地描绘出来，是抽象思维得以顺利进行的基础；综合表达了物理现象、本质规律及其内在联系，是具有物理意义的空间几何图形和数量关系的集合；是使我们更快、更准确地把握个物理量中的各种关系，找到恰当的突破口和解决问题的最佳方案；是分析、解决物理问题的必经之路. 构建物理图景不仅是物理思维的一种能力问题，更重要的是蕴含着一种思想、方法或者科学精神.实践证明，构建物理图景的过程就是培养物理素养的过程，也就是培养学生的形象思维能力、创造思维能力及模型构建能力的过程.教师在教学中不断引导学生活化物理过程和图景，能增强学生空间想象的自觉性，使空间想像力有充分锻炼的机会.为提高学生的解题能力，培养学生的形象思维能力、创造能力和空间想象能力，提供了一种有效的教学策略.

参 考 文 献

1赵凯华,等.新概念物理教程：力学.北京：高等教育出版社，2004

2哈尔滨工业大学理论力学教研室编.理论力学.北京：高等教育出版社，2002

3同济大学数学系.高等数学.北京：高等教育出版社，2007

竞赛与物理专题研修