从错误题解谈二重积分极坐标变换的积分限安排

从错误题解谈二重积分极坐标变换的积分限安排

陈凤德1陈柳娟2吕书龙1

(1.福州大学数学与计算机科学学院，福建福州350116；2.福建教育学院理科研修部，福建福州350025)

摘要：以学生的错误解答为切入点，给出二重积分极坐标变换下积分限安排的一点心得体会。

关键词：数学分析；二重积分；极坐标

作者简介：陈凤德(1974-)，男，福建屏南人，福州大学教授。

中图分类号：O175.14文献标识码：A

重积分的计算在数学分析课程中多变量积分学部分占有特别重要的地位，其掌握与否直接涉及到后续的曲线积分，曲面积分以及三大公式的学习，在二重积分的计算中，极坐标变换和广义极坐标变换是一个重要内容,而这部分内容并不容易掌握，文献[1-3]对极坐标系下积分限的安排进行了探讨，其中文[2-3]侧重从教师教学研究的角度进行了深入的理论探讨，文[1]则根据学生学习中出现的解题情况进行了探讨，回答了学生作业中出现的跟标准答案不一致的情况。笔者在教学中发觉哪怕限制角度变换范围到[0，2π]，由于受直角坐标系的影响，学生照样会出现错误。本文受论文[1]启发，也从学生的常见错解出发，来进一步谈谈学生该如何学习极坐标系下重积分积分限的安排。

由复旦大学数学系欧阳光中、朱学炎、金福临和陈传璋等老师[4]编写的《数学分析》(第三版)是国内很多高校数学系采用的教材,其下册第297页第7题的(3)(4)两小题：

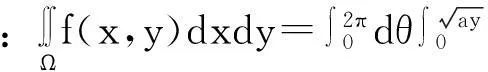
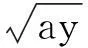
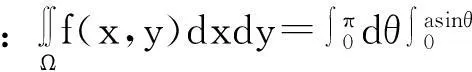
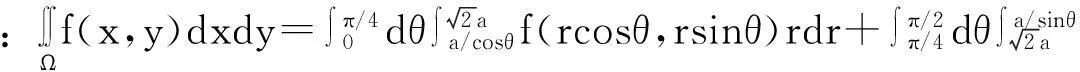
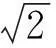
总体来说，教师在教学中要有意识的强调：(1)在直角坐标系下画出草图；(2)借助x=rcosθ,y=rsinθ确定边界方程r=r1(θ),r=r2(θ)；(3)强调的积分限安排要以固定的θ来确定，是从极角θ出发的射线跟r=r1(θ),r=r2(θ)的交点。经过这样的强调后学生在做作业时就可能会较少出现上述错误，或者在出现上述错误后，经过教师讲评也能较快理解自己的错误之处并进一步掌握正确的积分限安排手法。

参考文献：

[1]任丽平.用极坐标计算二重积分教学初探[J].吕梁高等专科学校学报,2009(1).

[2]高玉芬.重积分在极坐标变换下确定积分限的方法探究[J].青海师范大学学报(自然科学版),2012(1).

[3]袁荣.利用极坐标计算二重积分的方法与技巧[J].数学学习与研究,2012(1).

[4]欧阳光中,朱学炎,金福临，等.数学分析(下)(第三版)[M].北京：高等教育出版社,2010.