圆柱壳振动控制中约束阻尼拓扑优化研究

2016-01-11窦松然,桂洪斌,李承豪等

振动与冲击 2015年22期

圆柱壳振动控制中约束阻尼拓扑优化研究

窦松然，桂洪斌，李承豪，乔永亮

(哈尔滨工业大学(威海) 船舶与海洋工程学院，山东威海264209)

摘要：基于RAMP(Rational Approximation of Material Properties)插值模型密度法，以结构模态损耗因子倒数最小化为优化目标、阻尼结构体积为约束条件、约束阻尼单元相对密度为设计变量，建立约束阻尼结构拓扑优化模型。基于优化准则法推导设计变量更新准则，结合有限元法编写约束阻尼材料拓扑优化程序，对圆柱壳在振动控制中约束阻尼结构进行拓扑优化分析。结果表明，基于优化准则的振动拓扑优化方法所需迭代次数少，能有效减少结构的振动响应。从而验证设计方法的有效性。

关键词：拓扑优化；RAMP插值；密度法；优化准则法；约束阻尼；有限元

中图分类号:O328；TB535文献标志码：A

基金项目：国家自然科学基金资助项目(51208471)；高等学校博士学科点专项科研基金(20114101120008)；河南省科技攻关计划项目(142102210486)；郑州大学优秀青年教师发展基金(1421322059)

收稿日期：2014-05-19修改稿收到日期：2014-10-17

Topological optimization for constrained damping in vibration control of cylindrical shell

DOUSong-ran,GUIHong-bin,LICheng-hao,QIAOYong-liang(School of Naval Architecture and Ocean Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China)

Abstract:Structures with damping have a better performance in reducing vibration. Based on the density approach with RAMP interpolation model, a topologic model of constrained damping structure was established with the minimum of reciprocal of modal loss factors as a target function, the volume of damping structure as a constraint condition, and the relative density of constrained damping element as a design variable. The updating criterion of design variable was derived based on an optimal criteria method. And the topologic optimization program was developed based on the finite element method. The topological optimization for constrained damping structure in vibration control of cylindrical shell was carried out. The analysis shows that the topologic optimization method combined with the optimal criteria method needs less number of iterations and can reduce the vibration response of structure effectively, which indicates the validity of the design approach.

Key words:topologic optimization; RAMP interpolation; density approach; optimal criteria method; constrained damping; finite element

圆柱壳结构在潜艇、飞机等工程领域中应用较广，其振动普遍存在。为抑制结构振动，常在表面敷设约束阻尼[1]。在船舶、航空、汽车、土木等工程振动、噪声控制中，若将阻尼敷设于整个结构表面，并不能有效利用阻尼，会造成材料浪费；而实际中为减轻结构重量会减少阻尼敷设面积。因此如何正确敷设阻尼、提高结构减振效果成为研究解决的重要问题。

对约束阻尼圆柱壳振动已有诸多研究。Bieniek[2]提出约束阻尼圆柱壳受迫振动研究方法，并对载荷垂直壳体中性面情形进行分析。Rahmani等[3]用高阶夹层板理论分析约束阻尼圆柱壳自由振动，研究几何参数对结构振动特性影响。Mohammadi等[4]用半解析有限元法对约束阻尼圆柱壳的阻尼特性进行线性、非线性分析，研究夹层间滑移对模态损耗因子影响。

由于工程中对材料用量要求严格，且在约束阻尼体积减少合适前提下，部分敷设约束阻尼减少材料用量亦能获得更好减振效果，因此约束阻尼结构优化得到重视。杨德庆等[5]用阻尼拓扑灵敏法对短边固支的自由阻尼板布局形式进行优化。Zheng等[6]用遗传算法研究约束阻尼梁结构在布局的优化问题。Araujo等[7]用直接多元搜索法对约束阻尼夹层板进行多目标拓扑优化。张志飞等[8]基于优化准则法编制阻尼材料的拓扑优化程序，并结合有限元法对铝板阻尼材料布置进行优化。Cameron等[9]结合拓扑、尺寸及性能优化使约束阻尼板结构与声学性能达到最优。以上文献所用模型大多为梁、平板，模型较简单，而采用圆柱壳作为优化模型的研究较少。Kumar等[10-11]通过实验对约束阻尼圆柱壳阻尼层位置进行优化，并研究部分敷设主动约束阻尼层的振动特性。石慧荣等[12]分析局部敷设约束阻尼圆柱壳，讨论阻尼段结构参数变化对振动特性影响。李超等[13]用渐进结构法对圆柱壳结构进行的拓扑优化，缺乏严格数学推导，且在迭代过程中删除的单元不能恢复，易获得局部最优解。

结构材料插值模型及拓扑优化方法为拓扑优化技术基础，而密度法为具有代表性的插值方法常用于工程中。密度插值模型有固体各向同性微结构惩罚模型(Solid Isotropic Microstructures with Penalization, SIMP)及材料属性合理近似模型(Rational Approxim- ation of Material Properties，RAMP)，且RAMP较SIMP稳定性更好，更适合动力学分析[14]。拓扑设计中主要优化方法有优化准则法(OC)及数学规划法(MP)。因圆柱壳结构在工程领域广泛应用，研究其减振及阻尼拓扑优化有重要理论意义与实际工程价值。本文基于RAMP插值密度法建立约束阻尼结构拓扑优化模型，推导结构模态目标函数灵敏度表达式，用优化准则研究圆柱壳在振动中约束阻尼拓扑优化问题。

1基于RAMP插值的拓扑优化模型

对约束阻尼结构而言，为使其在振动中能量耗散达到最大，常以结构模态损耗因子最大化作为优化目标。为方便得到通用更新格式，以损耗因子倒数最小化为优化目标、约束阻尼单元相对密度xi为设计变量、优化后阻尼材料体积为约束条件，建立圆柱壳约束阻尼拓扑优化模型，即

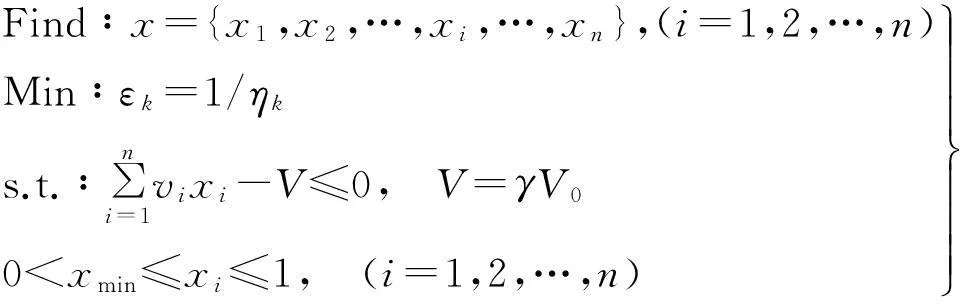
式中：ηk为第k阶损耗因子；vi为单元体积；V0为优化前初始体积；V为优化后体积；γ为约束体积分数；xmin为设计变量下限值。

据模态应变能理论，约束阻尼结构第k阶模态损耗因子倒数为

(2)

式中：ηc为阻尼层损耗因子；Uck为结构第k阶模态应变能；Uk为阻尼层第k阶模态应变能。

式(2)两边对相对密度xi求导，得

(3)

式中：Udk为基层、约束层第k阶模态应变能之和。

(4)

式中：ui为单元i的位移向量；Kci为单元i中对应阻尼层单元刚度矩阵。

据结构动力学理论，对第k阶模态特征值λk及特征向量φk满足运动方程的特征方程及振型正交性条件为

(K-λkM)φk=0,φTkMφk=1

(5)

将式(5)求导并代入式(4)，得

(6)

式中：Mci为单元i中对应阻尼层单元质量矩阵。

同单元约束层与阻尼层位移向量相同，则有

(7)

式中：Mri，Kri为单元i中对应的约束层单元质量、刚度矩阵。

由RAMP理论，设初始材料密度为1的单元，则单元密度、弹性模量可表示为

(8)

整理各式获得结构第k阶模态目标函数灵敏度为

(9)

2基于优化准则法的设计变量更新、收敛准则

优化准则法(OC)在工程上以一定假设为基础，建立优化设计迭代公式迭代求解。此法与结构变量多少及复杂程度无关，迭代次数较少，因此适合大型结构优化设计。实际结构的设计变量上万个，可利用优化准则法对设计变量进行更新，优化结构。利用拉格朗日乘子法将有约束最优问题转化为无约束最优问题，构造拉格朗日函数，即

λ2(xmin-xi)+λ3(xi-1)

(10)

式中：λ1，λ2，λ3为拉格朗日乘子。

(11)

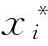
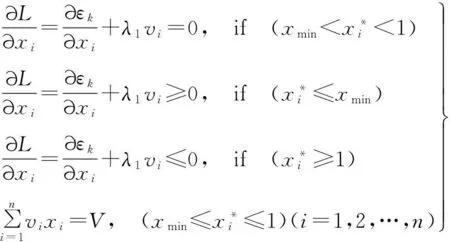
(13)

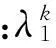
(14)

式中：σ(k+1)=ασ(k)为惩罚系数，α>1为放大系数；ξ为阻尼因子，保证计算的收敛性及稳定性；m为变量更新限值。

设计变量更新后需通过收敛准则检查结果是否收敛，据乘子法收敛性知，收敛判定准则为

(15)

即，每次迭代后的体积与目标约束体积差值绝对值需小于极小值。ε为收敛精度。

3约束阻尼结构阻尼优化步骤及流程图

用优化准则法基于RAMP插值的约束阻尼结构振动拓扑优化步骤为：①确定设计变量及非设计变量，初始化设计变量xi，据RAMP插值模型设置变量单元材料属性，建立有限元模型；②对约束阻尼结构进行模态分析，计算整个结构第k阶模态应变能、动能及相对设计变量的灵敏度；③据优化准则法求解拉格朗日乘子，进行变量更新；④据收敛判定准则判定是否满足收敛条件，若不满足则转到②，满足则进行⑤；⑤输出设计变量及其它结果，结束计算。

基于优化准则法的振动拓扑优化流程图见图1。

4约束阻尼圆柱壳振动阻尼优化

以长500 mm，半径100 mm，两端采用完全固定边界条件的约束阻尼圆柱壳为研究对象。材料阻尼层损耗因子为0.8，其它材料参数见表1。

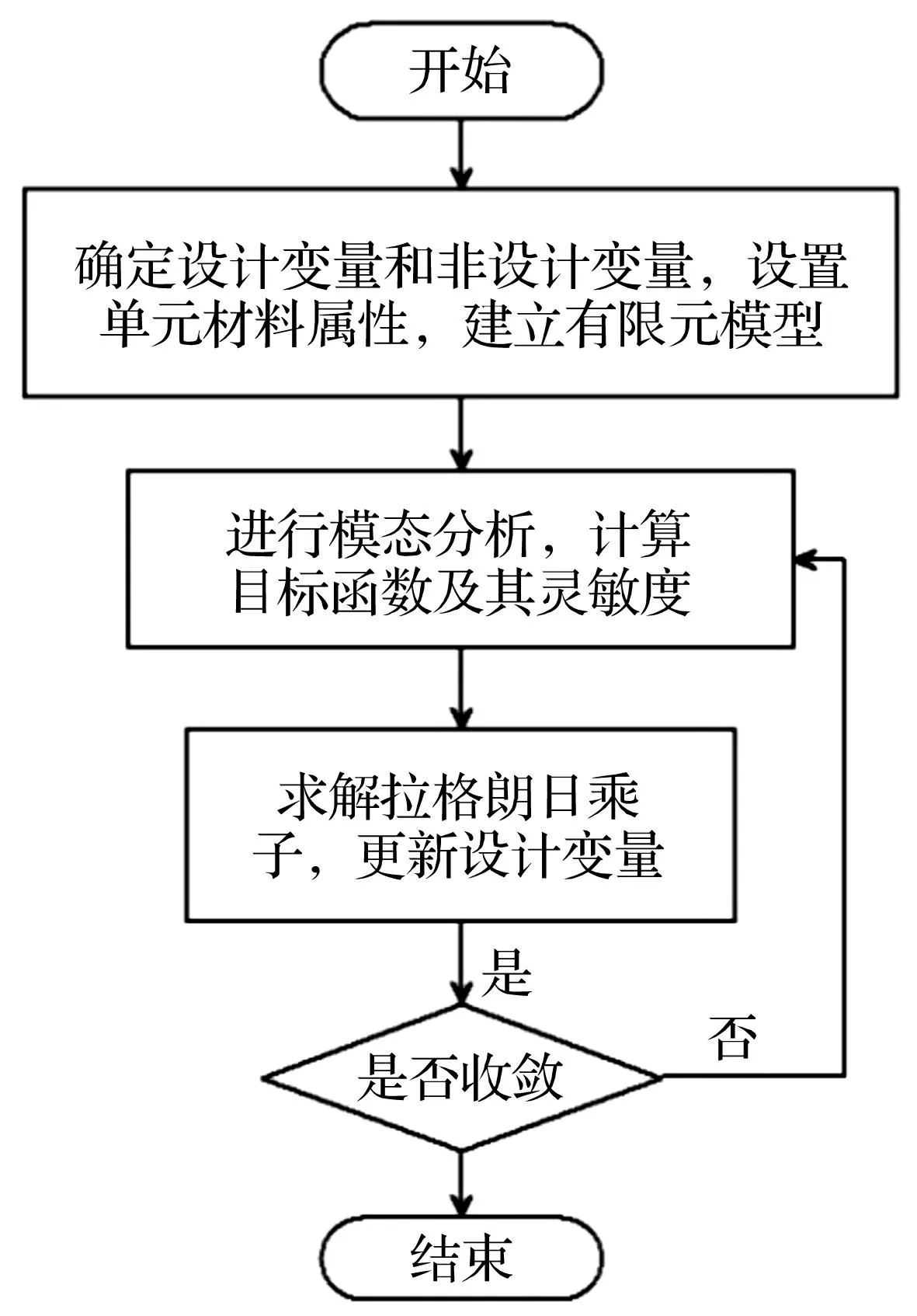
图1　约束阻尼结构拓扑优化流程图 Fig.1 Flow chart for topological optimization of constrained layer damping structure

厚度/mm弹性模量/Pa泊松比密度基层 22.1×10110.37800阻尼层12.3×1070.41340约束层22.1×10110.37800

图2　约束阻尼圆柱壳有限元模型 Fig.2 FEM of cylindrical shell with constrained damping

不同阶模态阻尼材料拓扑优化分布见图3。由图3看出，对中心对称的圆柱壳结构，阻尼材料也关于中轴呈对称分布。随模态阶数增加、振型变复杂、阻尼材料优化分布也变复杂，且优化的阻尼材料均未分布在边界处。优化前后不同阶模态振型见图4、图5。由2图看出，阻尼材料最优分布与模态振型联系紧密。圆柱壳中间响应较大，阻尼材料大部分分布在此片区域。而在临近边界处，由于受边界条件限制，圆柱壳响应较小，因此阻尼材料在此区域分布较少。

图3　拓扑优化后阻尼分布 Fig.3 Damp distribution after topological optimization

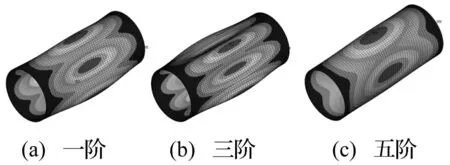
图4　拓扑优化前结构振型 Fig.4 Vibration type before topological optimization

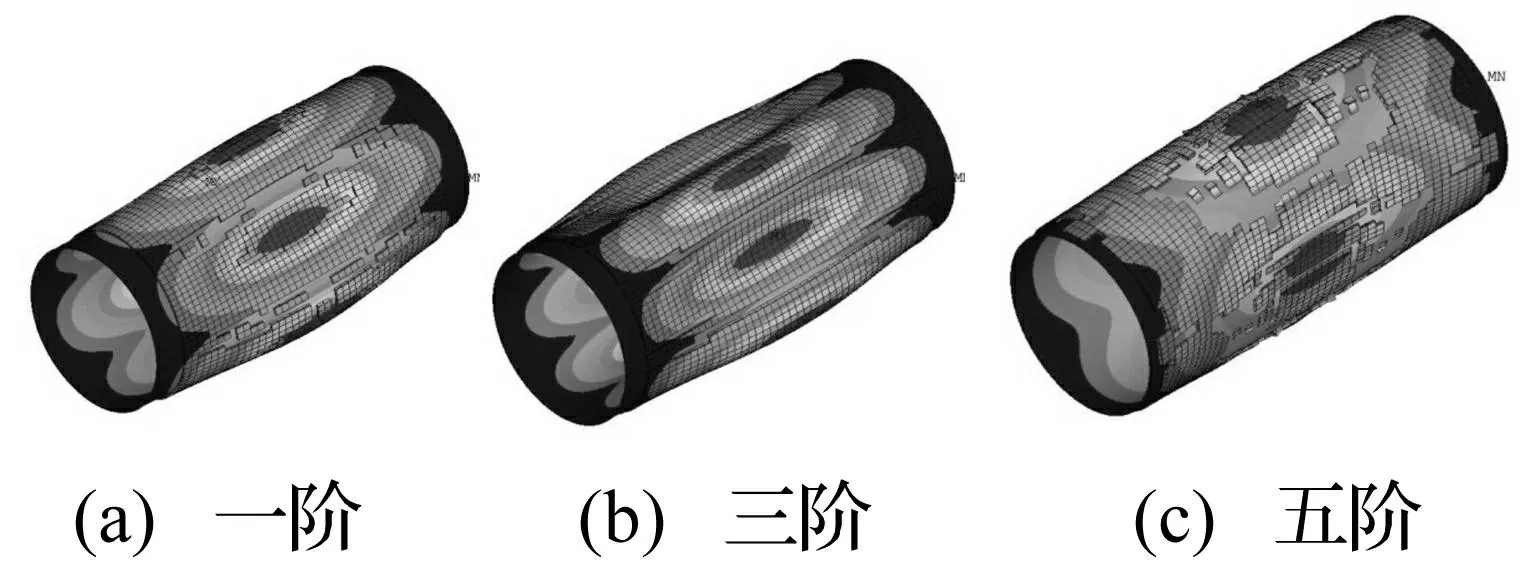
图5　拓扑优化后结构振型 Fig.5 Vibration type aftertopological optimization

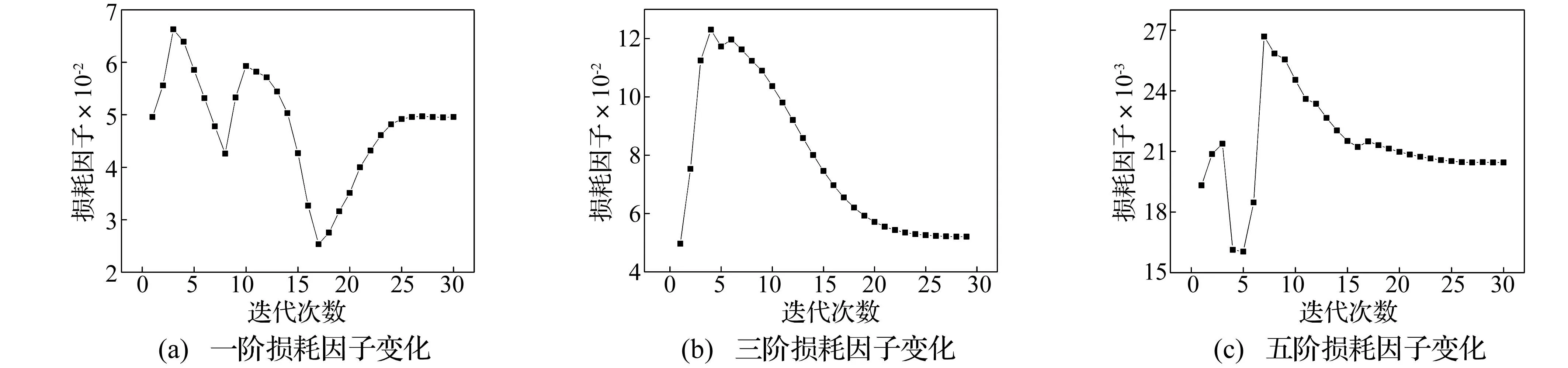
图6　模态损耗因子变化过程 Fig.6 Change process of modal loss factor

模态损耗因子随迭代次数变化见图6。由图6看出，每阶迭代过程均在一定波动后逐渐达到稳定平衡，最终收敛。一阶模态经30次迭代达到收敛，三阶经29次达到收敛，五阶经30次达到收敛，说明基于优化准则法的振动拓扑优化所需迭代次数较少，对每阶模态优化所需迭代次数基本相同。

拓扑优化前后各阶损耗因子变化见表2。由表2看出，拓扑优化后结构损耗因子有较小提升，一阶损耗因子增长8.5%，三阶增长6.4%，五阶增长6.2%。说明在约束阻尼减少合适情况下可通过拓扑优化，使阻尼材料利用率最大化，并在节省阻尼材料前提下提升结构的阻尼性能。计算达到预期优化目标，从而验证利用优化准则法的圆柱壳振动拓扑优化有效性。

表2　拓扑优化前后各阶损耗因子

5结论

基于RAMP插值建立约束阻尼结构拓扑优化模型，推导结构模态目标函数灵敏度表达式，提出基于优化准则法的振动拓扑优化方法。用优化准则法编写程序，建立约束圆柱壳模型，研究约束阻尼圆柱壳结构阻尼拓扑优化，结论如下：

(1)利用基于优化准则法的振动拓扑优化方法分析阻尼结构可有效减少结构振动响应，且计算中所需迭代次数较少。

(2)用优化准测法对约束阻尼圆柱壳结构阻尼进行拓扑分析可有效提高阻尼材料利用率，在合适减少阻尼材料情况下，亦可增加结构的损耗因子，获得最大能量耗散，降低结构振动响应。

(3)对约束阻尼圆柱壳结构阻尼优化后，可将阻尼材料大部分敷设在结构振动响应较大区域，响应较小区域则不敷设，能最大限度降低结构响应。阻尼材料敷设形式的复杂程度随结构振型的复杂增加。

(4)基于优化准则法编写程序对约束阻尼结构阻尼布局优化，理论推导严谨，用于工程切实可行。

参考文献

[1]李以农,谢熔炉,王宜,等. 约束阻尼结构拓扑优化设计的进化算法[J]. 重庆大学学报:自然科学版, 2010, 33(8):1-6.

LI Yi-nong, XIE Rong-lu, WANG Yi, et al. Topology optimization for constrained layer damping material in structures using ESO method[J]. Journal of Chongqing University: Natural Science Edition, 2010, 33(8): 1-6.

[2]Bieniek M P. Forced vibrations of cylindrical sandwich shells[J]. Journal of the Aerospace Sciences, 1962,29(2): 180-184.

[3]Rahmani O, Khalili S M R, Malekzadeh K. Free vibration response of composite sandwich cylindrical shell with flexible core[J]. Composite Structures, 2010, 92(5): 1269-1281.

[4]Mohammadi F, Sedaghati R. Linear and nonlinear vibration analysis of sandwich cylindrical shell with constrained viscoelastic core layer[J]. International Journal of Mechanical Sciences, 2012, 54(1): 156-171.

[5]杨德庆,柳拥军. 自由阻尼层结构阻尼材料配置优化的拓扑敏度法[J]. 振动工程学报, 2004, 16(4): 420-425.

YANG De-qing, LIU Yong-jun.Topological sensitivity method for the optimal placement of unconstrained damping material in structures[J].Journal of Vibration Engineering,2004,16(4):420-425.

[6]Zheng H, Cai C, Tan X M. Optimization of partial constrained layer damping treatment for vibrational energy minimization of vibrating beams[J].Computers & Structures,2004, 82(29): 2493-2507.

[7]Araujo A L, Madeira J F A, Mota Soares C M, et al. Optimal design for active damping in sandwich structures using the Direct MultiSearch method[J]. Composite Structures, 2013, 105: 29-34.

[8]张志飞,倪新帅,徐中明,等. 基于优化准则法的自由阻尼材料拓扑优化[J]. 振动与冲击, 2013, 32(14): 98-102.

ZHANG Zhi-fei, NI Xin-shuai, XU Zhong-ming, et al.Topologic optimization of a free damping material based on optimal criteria method[J]. Journal of Vibration and Shock, 2013, 32(14): 98-102.

[9]Cameron C J, Lind Nordgren E, Wennhage P, et al. On the balancing of structural and acoustic performance of a sandwich panel based on topology, property, and size optimization[J]. Journal of Sound and Vibration, 2014, 333(13): 2677-2698.

[10]Kumar N, Singh S P. Experimental study on vibration and damping of curved panel treated with constrained viscoelastic layer[J]. Composite Structures, 2010,92(2): 233-243.

[11]Kumar N, Singh S P. Vibration control of curved panel using smart damping[J]. Mechanical Systems and Signal Processing, 2012, 30: 232-247.

[12]石慧荣,高溥,李宗刚,等. 局部约束阻尼柱壳振动分析及优化设计[J]. 振动与冲击, 2013, 32(22):146-151.

SHI Hui-rong, GAO Pu, LI Zong-gang, et al. Vibration analysis and optimization design of a cylindrical shell treated with constrained layer damping[J]. Journal of Vibration and Shock, 2013, 32(22):146-151.

[13]李超,李以农,施磊,等. 圆柱壳体阻尼材料布局拓扑优化研究[J]. 振动与冲击, 2012, 31(4): 48-52.

LI Chao, LI Yi-nong, SHI Lei, et al. Topological optimization for placement of damping material on cylindrical shells[J].Journal of Vibration and Shock, 2012, 31(4): 48-52.

[14]李家春,叶邦彦,汤勇,等. 基于密度法的热传导结构拓扑优化准则算法术[J].华南理工大学学报:自然科学版, 2006, 34(2):27-32.

LI Jia-chun, YE Bang-yan, TANG Yong, et al.Algorithm of topology optimization criteria for heat conduction structure based on density approach[J].Journal of South China University of Technology:Natural Science Edition,2006,34(2):27-32.

[15]李攀. 约束阻尼结构动力学拓扑优化方法研究[D]. 重庆:重庆大学, 2013.

[16]郑玲,谢熔炉,王宜,等. 基于优化准则的约束阻尼材料优化配置[J]. 振动与冲击, 2010, 29(11): 156-159.

ZHENG Ling, XIE Rong-lu, WANG Yi, et al.Optimal placement of constrained damping material in structures based on optimality criteria[J]. Journal of Vibration and Shock, 2010, 29(11): 156-159.