基于相空间重构与平稳子空间分析的滚动轴承故障诊断

基于相空间重构与平稳子空间分析的滚动轴承故障诊断

刘尚坤，唐贵基，庞彬

(华北电力大学机械工程系，河北保定071003)

摘要：针对如何分离淹没在与转子转速相关的背景信号及其它噪声中的滚动轴承故障特征信号问题，提出将相空间重构与平稳子空间分析相结合的滚动轴承故障诊断方法。用相空间重构实现对滚动轴承故障振动信号升维；用平稳子空间对高维信号中平稳、非平稳源信号进行区分，并对峭度值最大的非平稳源信号进行最小熵解卷积降噪；对降噪信号进行包络谱分析提取轴承故障特征频率。仿真信号、故障诊断实例表明，诊断效果优于基于EMD的包络解调方法。

关键词：相空间重构；平稳子空间分析；最小熵解卷积；滚动轴承；故障诊断

中图分类号:TH133.3；TH165+.3文献标志码：A

Fault diagnosis for rolling bearings based on phase space reconstruction and stationary subspace analysis

LIUShang-kun,TANGGui-ji,PANGBin(Mechanical Engineering Department, North China Electric Power University, Baoding 071003, China)

Abstract:Rolling bearing’s fault feature signals are non-stationary, transient and often submerged in background signals associated with the components of rotating speed and other noises. How to separate the fault feature signals from the rolling bearing’s blind sources is an important issue. A method combining the phase space reconstruction technique with the stationary subspace analysis (SSA) was proposed. The fault vibration signal’s dimension was increased by the phase space technique and the non-stationary source components in the high-dimensional signals were distinguished from the stationary components by using the SSA. Then, the selected non-stationary component with the maximum kurtosis value was de-noised by the minimum entropy deconvolution (MED). Finally, the de-noised non-stationary component was analyzed by the envelope spectrum to extract the fault characteristic frequency. The simulation and experiment results indicate that the proposed method can extract the fault frequency better than the envelope demodulation method based on empirical mode decomposition (EMD).

Key words:phase space reconstruction; stationary subspace analysis; minimum entropy deconvolution; rolling bearing; fault diagnosis

滚动轴承作为旋转机械系统核心元件之一，对旋转机械设备的正常运行至关重要。由于承受载荷复杂且工作环境特殊，滚动轴承亦为脆弱部件之一，约30%的机械故障由滚动轴承引起。因此对滚动轴承故障特征诊断，尤其早期微弱故障诊断意义重大[1]。

相空间重构技术是为非线性问题处理方法[2]，适用于机械冲击故障的典型非线性特点，已证明重构高维相空间与系统的动力学特征相同，能在高维空间反映各故障状态下系统的动力学特征更清晰[3]。平稳子空间分析法(Stationary Subspace Analysis，SSA)可从高维信号中分离出平稳源、非平稳源信号[4-5]。较独立分量分析等传统盲源分离方法，该方法对原信号各分量的独立性并无要求。SSA方法已在地球磁场动态数据分析[6]、脑电信号分析[7]、高维信号突变点监测[8]等得到成功应用，并被逐渐引入故障诊断领域[9]。

将相空间重构结合盲源分离方法对多源盲信号分析可有效分离出原信号中的独立信号源。如相空间重构与独立分量分析(Independent Component Analysis，ICA)结合方法提取滚动轴承周期性故障冲击信息[10]，再如基于相空间重构与ICA的局部投影独立算法进行信号降噪分析，并用于滚动轴承故障诊断[11]。滚动轴承故障振动信号可视为由故障特征信号与转频相关背景信号、噪声等组成的多分量信号。本文将相空间重构与新盲源分离方法-平稳子空间分析结合进行滚动轴承故障信号提取。用相空间重构实现滚动轴承故障振动信号升维，利用平稳子空间对高维信号中平稳、非平稳源信号进行区分，并对峭度值最大非平稳源信号进行最小熵解卷积(Minimum Entropy Deconvolution，MED)降噪，对降噪信号进行包络谱分析提取轴承故障特征频率。

1相空间重构技术

相空间重构技术为时间序列分析方法，对一维时间序列，用该技术可扩展到高维相空间。相空间重构目的为从高维空间恢复出混沌吸引子。因其含重要的系统分量信息。对离散时间信号xi(i=1,2, 3,…N)，选择嵌入维数d及时间延迟τ，可重构一个d维相空间，即

X=

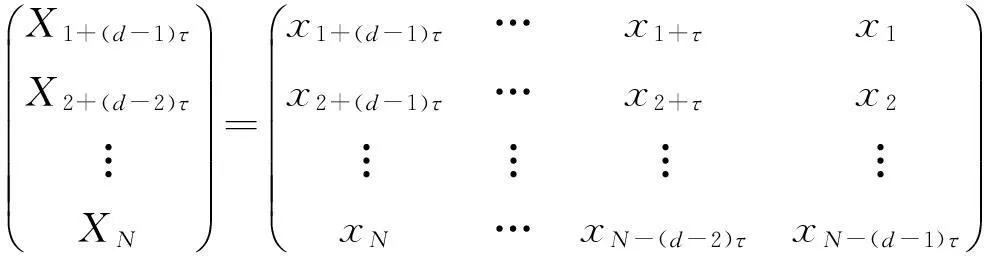
(1)

式中：Xi为第i相点，表示d维相空间中一个态。

在相空间重构中，时间延迟及嵌入维数选择非常重要，直接决定相空间矩阵能否真实反映隐含在时间序列中的非线性规律及动力学特征，间接影响SSA方法的分析效果。交互信息方法及伪临近点方法计算的时间延迟τ及嵌入维数d。

2平稳子空间分析与最小熵解卷积降噪

2.1平稳子空间分析方法

SSA算法核心思想即将多维时间序列分解为平稳、非平稳部分。设D维观测信号x(t)含m维平稳源信号ss(t)=[s1(t),…,sm(t)]T及D-m维非平稳源信号sn(t)=[sm+1(t),…,sD(t)]T，则存在一个可逆混合矩阵A，使

(2)

式中：As，An为列向量，生成的空间称为平稳(s-)空间、非平稳(n-)空间。

(3)

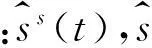
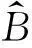
(4)

由式(5)最小化目标函数

(5)

(6)

(7)

2.2最小熵解卷积降噪

由于SSA分析的非平稳信号由最大化非平稳性获得，该非平稳源信号分量会受噪声等干扰。设离散信号y(n)为SSA分解所得任意一非平稳源信号，则y(n)可描述为由滚动轴承局部损伤故障引起的冲击信号x(n)与传递响应函数h(n)卷积后，又叠加噪声干扰信号e(n)，即

一般而言，“顾忌”是中性词，而本文作者显然充分挖掘了“顾忌”一词的负面影响。仔细想来，非常有道理。正如作者所言：“内心足够强大，便可无所顾忌。”而相反，顾忌重重，则变成畏首畏尾，也就自然贻误了时机。阅卷经验告诉我们，好的议论文总有令人耳目一新的感觉，甚至于乍看起来，观点还有些“故作惊人之语”之嫌，而仔细一读，才觉很有道理。

y(n)=x(n)*h(n)+e(n)

(8)

为进一步抑制噪声干扰信号e(n)，突出非平稳源信号分量中的冲击信号x(n)，用最小熵解卷积(MED)对非平稳源信号分量y(n)进行降噪[12]，寻找一个逆滤波器w(n)，由y(n)恢复输入信号x(n)，即

x(n)=w(n)*y(n)

(9)

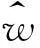
本文算法主要步骤为：①将一维待分析信号经相空间重构得到高维空间，即选择合适的时间延迟τ及嵌入维数d实现单通道信号升维。②结合嵌入维数d并据待分析信号具体情况确定SSA方法中平稳、非平稳源信号数目分析获得非平稳源信号。③对峭度值最大非平稳源信号进行最小熵解卷积(MED)降噪。④对降噪后非平稳源信号进行包络谱分析提取轴承故障特征频率。

3仿真信号分析

为验证本文算法提取非平稳源信号的有效性，构造多源信号x(t)。x(t)中非平稳源信号为滚动轴承外圈故障模拟信号x1(t)，平稳源信号由调幅调频信号x2(t)与正弦信号x3(t)组成，并加入噪声模拟信号x4(t)。其中f1=4 000 Hz, 外圈故障特征频率fo=45 Hz。各分量信号时域波形见图1，x(t)的时域波形见图2。时域波形并未表现出冲击特征。

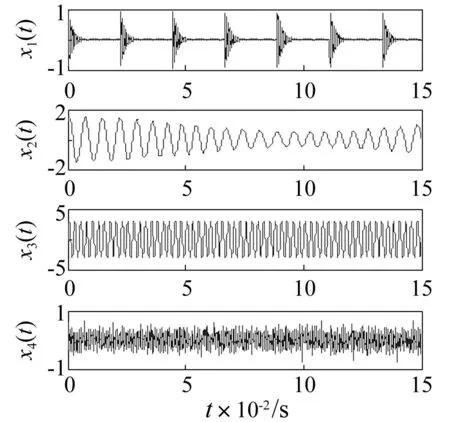
图1　x(t)各分信号时域波形 Fig.1 Time domain waveforms of x(t) component signals

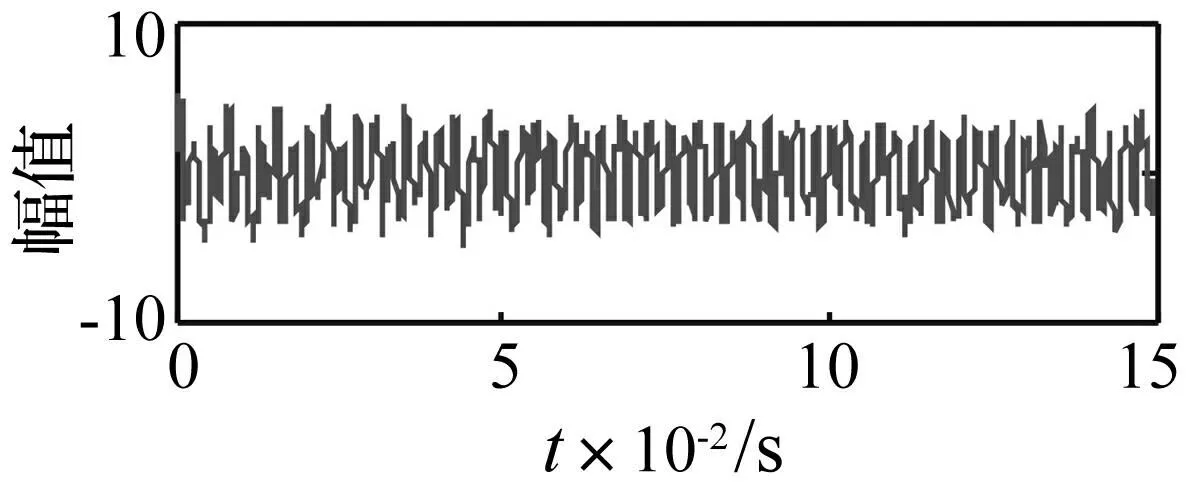
图2　x(t) 时域波形 Fig.2 Time domain waveform of x(t)

对x(t)进行相空间重构，嵌入维数d=4，将重构的4维时间序列为观察信号，用SSA算法对观察信号非平稳源信号进行提取。SSA算法分析结果见图3(a)，可知非平稳源信号峭度值为5.363，时域波形体现出与外圈故障模拟信号x1(t)一致的冲击特征，但噪声干扰严重，使冲击特征表现受到影响。经MED降噪后结果见图3(b)，可见非平稳源信号中噪声得到较大程度抑制，冲击特征更明显，非平稳源信号峭度值高达16.75。由此表明，本文算法能较好提取轴承故障特征信号的冲击特性。

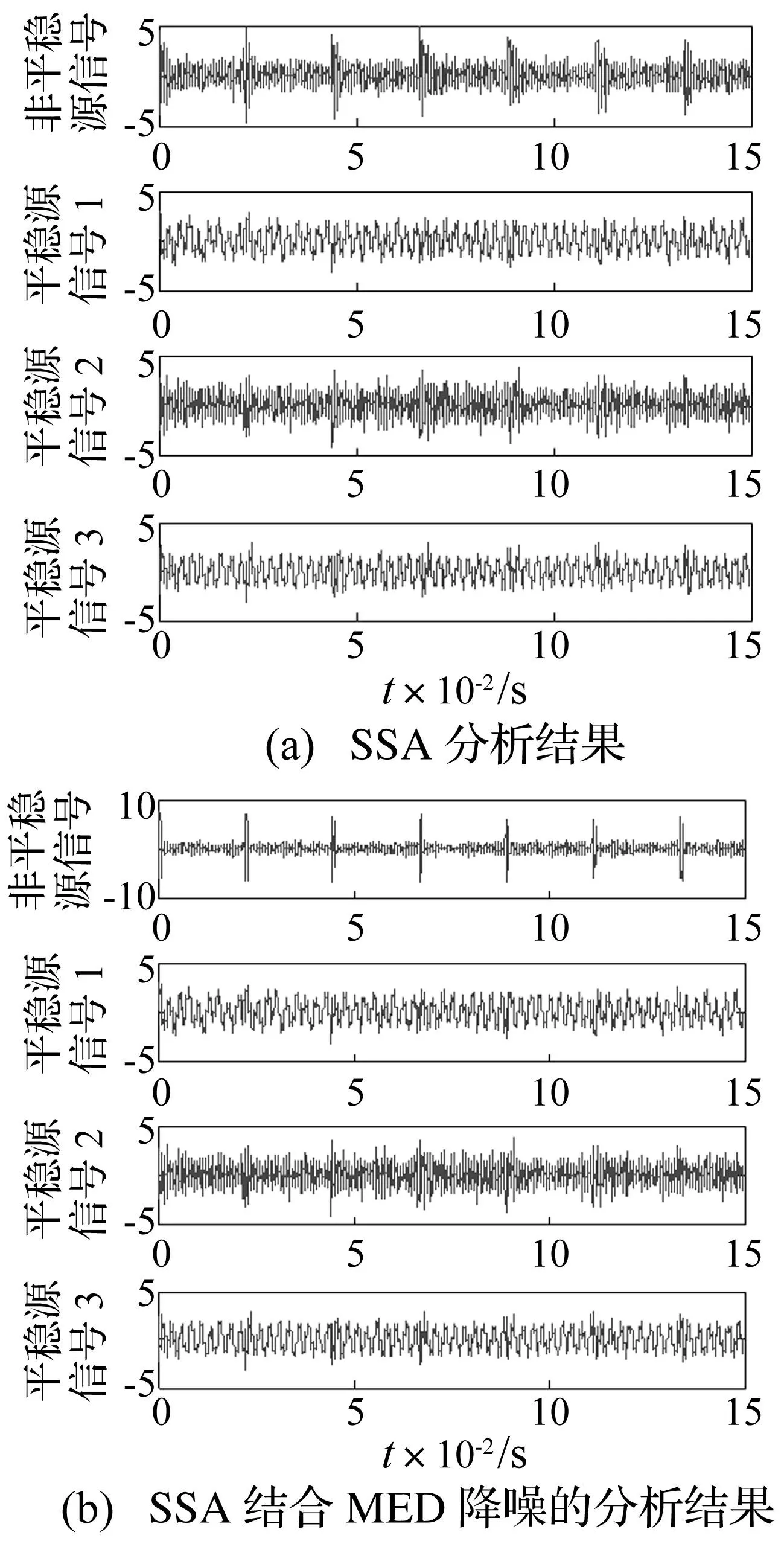
图3　仿真信号直接SSA分析及SSA结合MED降噪分析结果 Fig.3 The results of SSA analysis and SSA combined with MED denoising

将x(t)进行EMD分析，其中峭度值最大分量的时域波形见图4。由图4虽能看出故障冲击特征，但受噪声干扰较大，较本文方法分析效果较差。

图4　仿真信号EMD中峭度值最大分量时域波形 Fig.4 Time domain waveform of the max kurtosis component in EMD

4试验故障检测

通过QPZZ试验平台模拟滚动轴承内圈故障，试验台结构见图5。试验轴承型号为N205，在滚动轴承内圈线切割出一条0.5 mm深沟槽模拟滚动轴承故障。试验中对轴承端加载，并利用电涡流传感器及NI9234数据采集卡采集转轴振动信号，采样频率12.8 kHz。轴承节圆直径D=39 mm，滚动体直径d=7.5 mm，压力角α=0°，滚动体个数n=12，工作轴转速1 440 r/min。计算获得滚动轴承内圈故障特征频率fi=172 Hz。

图5　轴承故障试验平台 Fig.5 The test platform of bearing fault

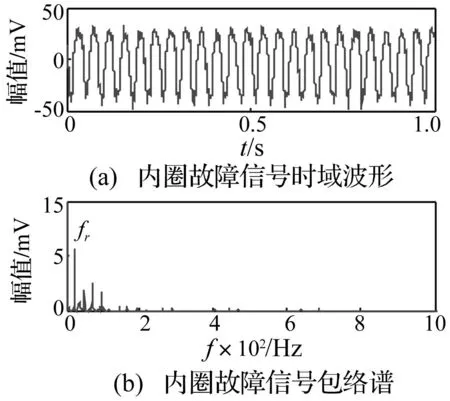
图6　内圈故障信号时域波形及包络谱 Fig.6 Time domain waveform and envelope of inner fault signal

对滚动轴承内圈故障振动信号进行相空间重构，延迟τ=1，嵌入维数d=4，将重构的4维相空间升维信号进行SSA算法分解，结果见图7(a)，可见非平稳源信号仍含较大程度转频及噪声成分干扰。两个非平稳源信号分量峭度值分别为6.674，5.328。经MED降噪的分量信号见图7(b)，可见两非平稳源信号分量的冲击特性更突出，噪声成分得到抑制，两非平稳源信号分量的峭度值分别为36.67，36.42。对降噪后峭度值最大非平稳源信号1的包络谱进行分析，结果见图8，图中可清晰识别内圈故障特征频率及倍频成分，连续倍频高达5阶。

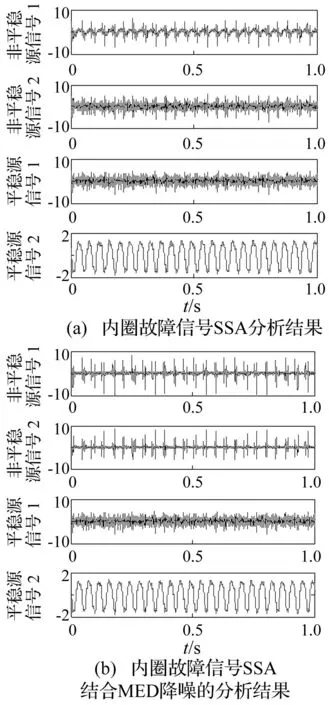
图7　内圈故障信号直接SSA分析及SSA结合MED降噪结果 Fig.7 The results of SSA analysis and SSA combined with MED denoising for inner fault signal

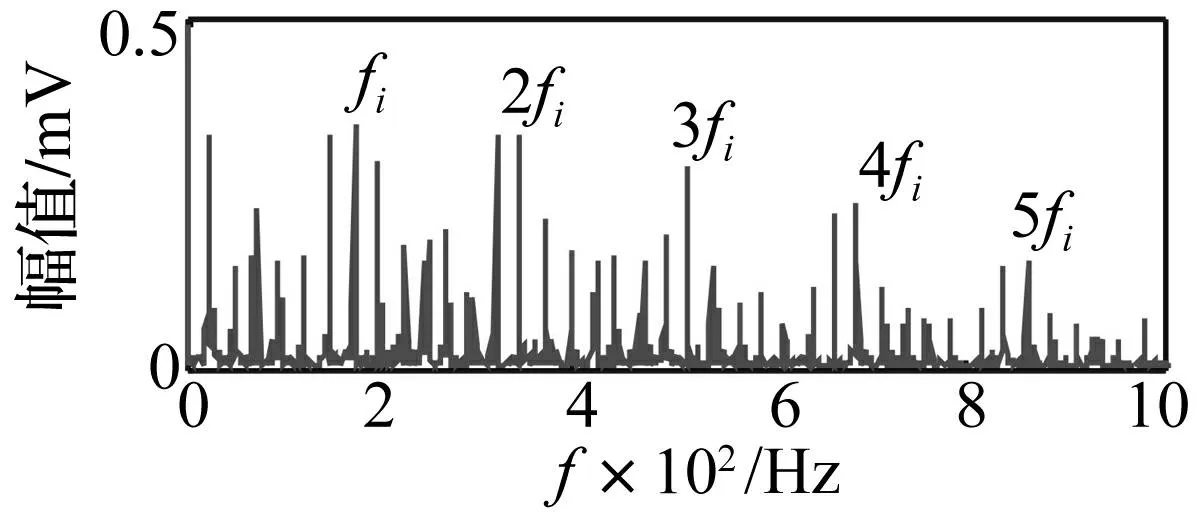
图8　包络谱分析结果 Fig.8 The result of envelope spectrum

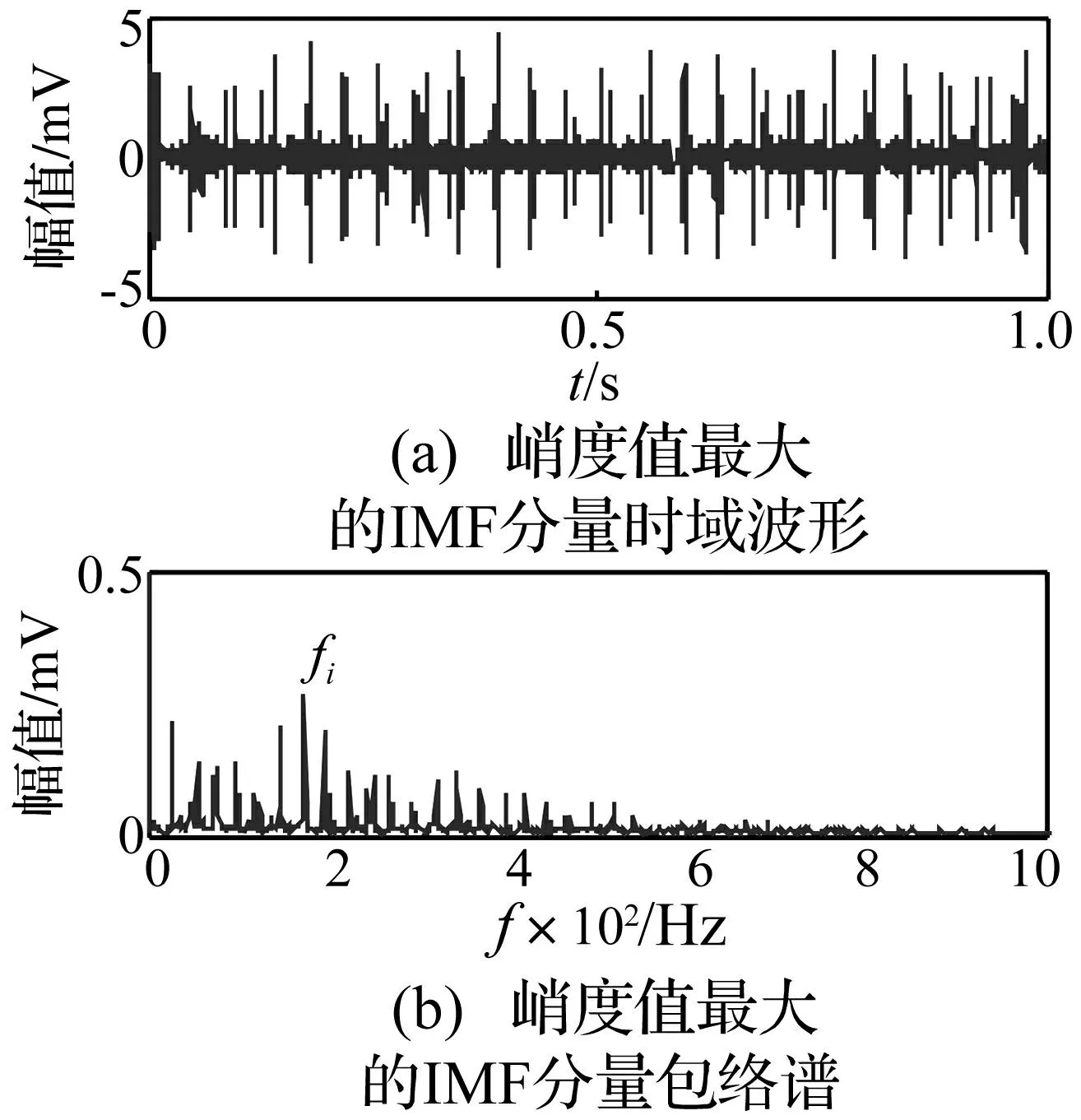
图9　内圈故障信号EMD中峭度值最大分量分析 Fig.9 The analysis of the max kurtosis component in inner fault signal’s EMD

为进一步验证本文方法的有效性，与基于EMD的包络谱方法进行对比分析。图9为对滚动轴承内圈故障振动信号进行EMD分解后，峭度值最大分量时域波形及包络谱，明显峰值频率为内圈故障特征频率，其它倍频并不突出。

5结论

(1)所提将相空间重构技术与平稳子空间分析相结合方法，可实现信号升维与分解。采用最小熵解卷积对分解的非平稳源信号降噪处理，再利用包络谱分析轴承故障频率特征。

(2)该方法能有效将单通道信号升维至高维空间并进行非平稳源信号分量提取，通过MED降噪能突出非平稳源信号分量的冲击特性，有效诊断滚动轴承故障。

(3)通过对比分析结果表明，本文方法优于基于EMD的包络谱分析方法，并可作为滚动轴承故障诊断的有效途径。

参考文献

[1]钟秉林,黄仁．机械故障诊断学[M]. 北京：机械工业出版社, 2007:298-313.

[2]Takens F. Detecting strange attractors in fluid turbulence [A]. Rand D, Young L S. Dynamical systems and turbulence[C]. Berlin: Springer, 1981:366-381.

[3]刘清坤,阙沛文,郭华伟,等．基于相空间重构和独立分量分析的超声信号噪声消除[J].上海交通大学学报, 2006, 40(10): 1739-1742.

LIU Qing-kun, QUE Pei-wen, GUO Hua-wei,et al. The noise cancellation for ultrasonic signals using reconstructed phase space and independent component analysis[J]. Journal of Shanghai Jiaotong University, 2006, 40(10): 1739-1742.

[4]Von Bunau P，Meinecke F C，Kiraly F，et al. Finding stationary sub-spaces in multivariate time series[J]. Physical Review Letters, 2009, 103(21): 214101.

[5]Kawanabe M,Samek W， von Bünau P，et al. An infor-mation geometrical view of stationary subspace analysis [J]. ICAA’11 Proceedings of the 21st International Conference on Artificial Neural,2011,6792: 394-404.

[6]Hara S，Kawahara Y，Washio T，et al. Separation of stationary and non-stationary sources with a generalized eigenvalue problem [J]. Neural Networks, 2012, 33: 7-20.

[7]Von Bunau P，Meinecke F C，Scholler S，et al. Finding stationary brain sources in EEG data[C]. The32nd Annual International Conference of the IEEEEMBS,Buenos Aires, Argentina,2010:2810-2813.

[8]Blythe D A J，Von Bunau P, Meinecke F C，et al. Feature extraction for change-point detection using stationary subspace analysis[J]. IEEE Transactions on Neural Network and Learning System, 2012,23(4): 631-643.

[9]严如强,钱宇宁,胡世杰,等．基于小波域平稳子空间分析的风力发电机齿轮箱故障诊断[J]. 机械工程学报,2014, 50(11): 9-16.

YAN Ru-qiang，QIAN Yu-ning，HU Shi-jie，et al. Wind turbine gearbox fault diagnosis based on wavelet domain stationary subspaces analysis[J]. Journal of Mechanical Engineering, 2014,50(11): 9-16.

[10]赵长生,姜立勇,蔡娟,等. 基于相空间重构的独立分量分析及其工程应用[J]. 轴承,2013(1): 51-54.

ZHAO Chang-sheng, JIANG Li-yong, CAI Juan, et al. Independent component analysis and its engineering application based on the phase space reconstruction[J]. Bearing,2013,(1): 51-54.

[11]黄艳林,李友荣,肖涵,等．基于相空间重构与独立分量分析局部独立投影降噪方法[J].振动与冲击,2011,30(1):33-36.

HUANG Yan-lin，LI You-rong，XIAO Han，et al. Local independent projection de-noising algorithm based on phase-space reconstruction technique and independent component analysis[J]. Journal of Vibration and Shock, 2011, 30(1): 33-36.

[12]Endo H，Randall R B. Enhancement of autoregressive model based gear tooth fault detection technique by the use of minimum entropy deconvolution filter[J]. Mechanical Systems and Signal Processing, 2007(21): 906-917.

[13]刘志川,唐力伟,曹立军.基于MED及FSK的滚动轴承微弱故障特征提取[J]. 振动与冲击,2014, 33(14): 137-142.

LIU Zhi-chuan, TANG Li-wei, CAO Li-jun. Feature extraction of rolling bearing’s weak fault based on MED and FSK [J]. Journal of Vibration and Shock, 2014, 33(14): 137-142.