用于雷达数据实时传输的LZW算法优化

2016-01-10

雷达科学与技术 2016年4期

(海军航空工程学院,山东烟台264001)

0 引言

船用导航雷达是一种用于船体探测周围目标,以便及时进行避让,进行自身定位等用的雷达,它能获得目标的距离、方位等基本信息[1]。为了实现雷达的远程显控,将其应用于无人值守雷达并实现雷达数据的入网共享功能,需要采集的雷达数据主要包括视频信号、触发脉冲、方位脉冲和船首脉冲四路信号。导航雷达扫描一帧所产生的数据量很大,要想实现雷达图像远程显示,需要将采集到的雷达数据实时回传给服务器,在服务器上进行实时图像显示,但由于网络传输带宽有限,直接进行数据传输效率低下,无法满足实时性要求,因此需要在数据传输前对其进行有效的压缩[2]。

针对实际雷达数据噪声和杂波多,数据熵值较大,且相邻帧之间相关性较高,采用LZW字典算法能达到很好的效果。但由于经典LZW压缩算法是基于字典的压缩算法,使用固定长度的码字对相继出现的、由单个信源符号所构成的、长度可变的符号序列进行编码,而不依赖于带编码信源符号出现的先验概率,因此在压缩比和压缩速率上还有很大提升空间。本文在原有LZW压缩算法的基础上,改变了字典查询的方式,通过空间换时间提升压缩速率,已达到数据实时传输的要求并满足无线网络带宽的限制。

1 实际雷达数据分析

在雷达天线获得的回波信号中,有需要的目标信号,为了方便雷达图像进行显示,需要将视频回波信号进行采集,同时包括触发脉冲、船首脉冲和方位脉冲三路同步信号。利用AD芯片,设计数据采集电路,将上述四路信号同时进行采集,使模拟信号转换为数字信号。本文主要以JMA2254雷达为研究对象,分析采集到的实际数据,其天线扫描周期是2 s,每个周期内完成2 048个方位的扫描,每个扫描线上采集2 000个点,那么通过计算可知其产生的数据率需要2 000×2 048×8/2=15.625 Mbit/s,保存一帧的雷达图像需要4 MB。对于现有的几种无线民用网络而言,只有4G网络才能勉强完成实时传输任务,但传输代价太大,且4G网络的传输距离有限,不适合远程传输工作,因此需要在进行数据传输前对其进行高效的压缩。

通过分析实际采集的雷达数据可知,相邻方位、相邻帧之间的雷达数据具有很高的相关性,从数据特点来讲具有很大的压缩空间。针对这种较高的数据相关性,LZW字典查询算法比较适合这类数据的压缩。图1是选取的任意两个相邻方位的数据进行的图像显示,以及两个方位相应距离点上的信号回波差值。从图1可以看出,方位间的数据相关性较大,对数据进行压缩前的预处理可以进一步提高压缩比。

通过对图1的分析可知,对雷达数据进行相关性处理,以其中一个方位为参考,其他方位可以用与参考方位的差值来表示。这样,原本需要8位二进制来表示一个距离点的数据,现在只需6位二进制来表示即可,经过预处理之后数据量会压缩到原来的75%,提高了压缩比。

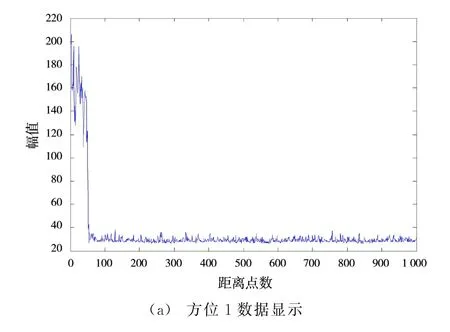
图1 相邻方位间的数据对比

2 LZW压缩算法

2.1 算法原理

LZW算法属于字典编码,根据数据本身包含重复代码的特性,用前面已经出现的字符串的代码来代替后面相同字符串的内容,从而实现数据压缩。由于该算法的压缩器不输出单个字符,只输出词典字符串中的代码,因此字典在开始时不能是空的,应该包含可能在字符流中出现的所有单个字符[3]。

该算法的基本思想是用简单的代码来代替复杂的字符串以实现数据的压缩,在压缩的过程中自适应建立一个字典,反映字符串与代码之间的对照关系,通过查询字典来确定字符串压缩代码的输出。

LZW编码能够有效地利用字符出现的频率冗余度、字符重复性和高使用率模式冗余度,不需要提前预测字符的概率分布,只要扫描一次字符,无需有关输入数据统计量的先验信息,并且运算时间和文件的长度成正比。

LZW压缩算法有3个重要的对象:数据流、编码流和编译表。在编码时,数据流是输入对象,编码流是输出对象;在解码时,编码流是输入对象,数据流是输出对象;编译表是在编码和解码时都要借助的对象。当编码的信源序列较短时,LZW编码性能将会有所下降,但当序列增长时,编码效率会提高,平均码长也会逼近信源熵[4]。LZW解码也比较简单,可以一边解码一边建立字典,只需要传输字典的大小,无需传输字典本身。

设长为L的信源序列μ分为M(μ)段码段,每段短语的二元码符号长度为[lgM(μ)+lgK],因此,μ编码后总码元长度为M(μ)·([lgM(μ)+lgK]),每个源符号的平均码长为

去掉向上取整符号,有下面不等式:

长度为l的段有K l种。若把长为L的信源序列μ分为M(μ)段码段之后,设最长段的长度为lmax,而且包含各种长度的所有段型,则

当lmax足够大时,式(3)和式(4)近似为M(μ)≈代入式(2),得到

设信源为平稳无记忆信源,信源符号的分布概率为P(a k),k=1,2,…,k,当lmax足够大时,典型的段中a k出现的次数接近lmaxP(a k)。这种段型的数目为Mlmax种,则

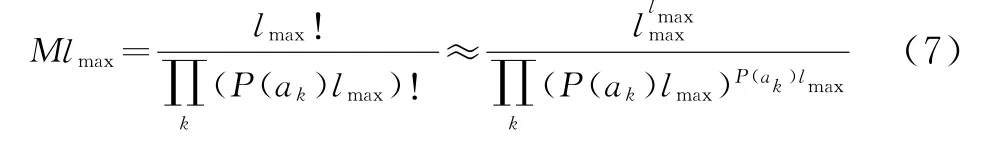
取对数,得

设较短的段型可以忽略不计,得

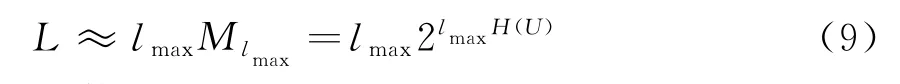
即总段数M(μ)≈M lmax,得到

将解码的信源序列趋于无穷时,lmax也趋于无穷,平均码长趋近于信源熵[5]。

2.2 算法实现

LZW是一种基于字典的算法。所谓字典算法,即认为信源输出的信息序列是由一本“字典”中的各种“词条”构成的。显然,该字典的词条应由信源符号的不同排列组合产生。但是该字典不是固定不变的,而是根据信源发出的编码动态地建立的。编码过程也就是建立字典的过程[6]。如果接收端建立的字典与发送端一样,就达到了正确的信息传送目的。LZW算法是围绕字典建立起来的一种压缩算法。通过字典,把输入的字符串映射成等长码字输出。LZW算法的字典具有前缀特性,这样就使得任何一个字典中字符串的前缀也一定在字典中。

LZW算法对每个输入字符串进行逐个字符检查,试图找到和字典已有字符串匹配的最长字符串并进行解析,这样字典内的编码项会越来越多,匹配几率也会随之增大,从而达到压缩目的。每个被解析了的字符串通过下一个输入字符扩展,这样形成的新字符串会被存入字典,新字符串会有一个新的标示符,称为编码值,并且同时输出前缀码的编码值。虽然LZW编码方式能够不依赖于数据的概率统计特征,但是会涉及到字典查找问题[7]。算法流程图如图2所示。

由于传统查找方式的查找效率太慢,故引入哈希函数[8],把哈希函数和传统LZW算法结合起来就形成了哈希和LZW的结合算法。此算法使得字典查找效率大大提高,由此增加了数据的压缩效率。

在编程实现过程中,用于压缩的哈希函数采用移位和基本算数运算来构造[9],这样哈希函数不仅运算速度快,易于硬件实现,而且比特之间的异或运算和位移运算能够提高哈希值的随机特性[10]。

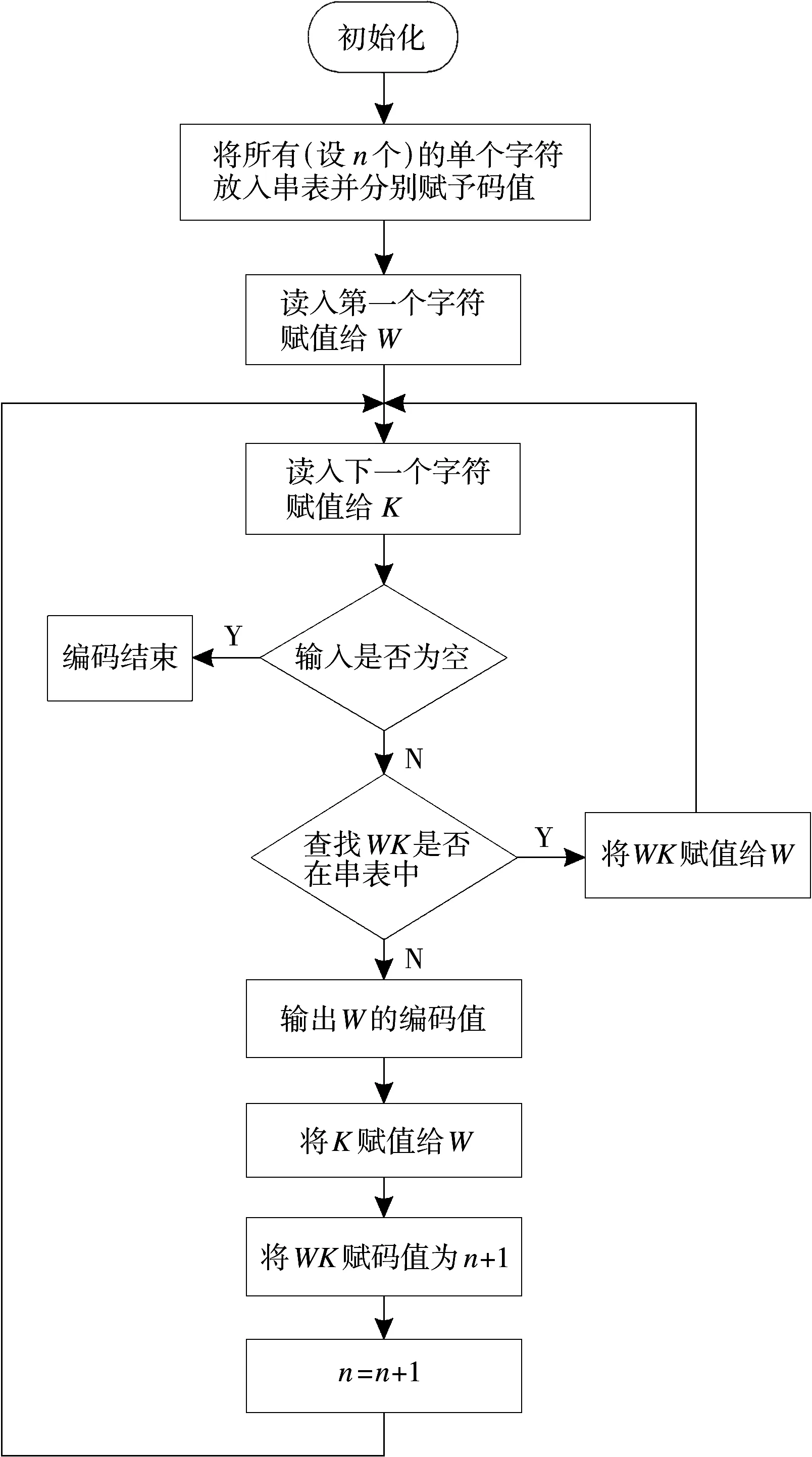
图2 LZW压缩算法流程图

将前缀W和后缀K加在一起形成新的字符串value,其中前缀W为字典中的编码,后缀K为新进的字符,将value通过上述位移运算生成一个key值,通过二叉树法对产生的key值进行查找对比,若已经存在,则原查找表中的key值对应的value中的前缀W即为新字符的字典编码;若不存在,则用新的编码来代替value中的前缀,继续进行上述查找过程[11]。

在查找过程中会不可避免地产生冲突以及哈希性能问题,需要对其进行不断的改进。

3 改进型LZW压缩算法

在基本LZW压缩算法的基础上,可以通过改变字典查找方式,加快查找速度,提高压缩效率。第2节介绍了通过引入哈希函数对字符串进行哈希变换,从而提高压缩效率的方法,但这种方法会涉及到哈希函数的选择以及产生冲突的问题,对于编程实现较复杂。

现对字典查找方式进行适当改变,利用“空间换时间”的思维进行查找[12]。

建立一个数组,大小是:字典大小×根字符数×字节数。在本次实际应用中,选择建立字典的大小为4 096,根字符数为256个,每个数据为2个字节,那么建立的数组大小为4 096×256×2=2 MB。将数组定义为uint8 dict[4 096][256],具体流程如图3所示。

图3 改进LZW字典查找算法流程图

从上述算法流程图可以看出,改进的算法每一步只需一次查找,查找速度非常快,但这个高速查找是通过大量消耗内存为代价的,这就是所谓的“空间换时间”算法[13]。随着科技的不断进步,几兆内存对于计算机而言非常小,不会影响其正常工作,而且对于FPGA、ARM等嵌入式系统和芯片来说,随着技术的不断改进,其内存也不断增大,开辟几兆内存供压缩使用提高压缩效率也是值得的。

4 压缩结果分析

以实际采集到的雷达数据为压缩对象,运用基本遍历查找的LZW压缩算法、哈希函数查找的LZW压缩算法、改进的空间换时间LZW压缩算法,以及WinRAR软件四种方式对同一数据进行压缩,通过对比,体现改进算法的优势。表1是4种方法对30 MB雷达数据进行压缩的效率对比。

表1 不同算法压缩效率对比

通过对表1压缩效率对比分析可以看出,基本遍历算法的压缩效率是30/739.516≈0.04 MB/s,哈希函数算法的压缩效率是30/134.643≈0.22 MB/s,本文算法的压缩效率是30/3.898≈7.69 MB/s,Win RAR软件的压缩效率是30/5=6.00 MB/s。对于同一数据,压缩效率差距很大,而本文在第1节中就对实际雷达数据进行分析,雷达一帧的数据是4 MB,扫描周期是2 s,也就是说每秒要压缩至少2 MB才能满足实时传输的要求,而基本遍历算法和哈希函数算法都不能达到这个要求,这就会引起数据堆积,占用大量的缓存,不适合实时传输;本文的算法和Win RAR都能很好地达到2 MB/s的速率要求,实现传输的实时性,且本文提出的算法还略胜于Win RAR软件。

表2是4种方法的压缩比对比,以及其实时传输所需的传输带宽。

表2 不同算法压缩比结果对比

通过对表2压缩比对比分析可知,经过预处理后的空间换时间算法大大提高了压缩比,且对于第1节提供的实际雷达数据,数据率是15.6 Mbit/s,本文相对于其他方法,压缩程度更大,所需的传输带宽更小,更容易实现无线网络的实时传输,从而进一步提高了压缩效率,使其更加符合实时性传输的要求。

从表1、表2的分析中可以看出,本文提出的空间换时间算法在压缩效率和压缩比上更具有明显的优势,更能实现数据的实时传输。

由于LZW压缩算法是一种无损压缩算法,通过反向解压,可以将数据完整地解压出来,与原始数据保持一致。而本文提供的空间换时间算法也是在LZW的基础上进行的改进,其解压后的数据也保持了一致性。

利用空间换时间的算法对实际雷达数据进行压缩,达到了实时性的要求,通过图像显示,使采集后的数据能经过传输后实时显示出来,显示效果如图4所示。

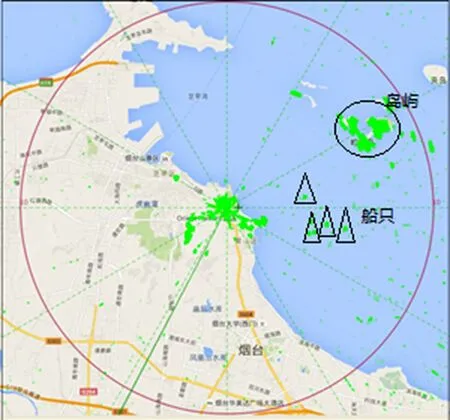
图4 雷达图像实时显示图

这是在某海边的一部导航雷达所收到的回波信号,将数据采集、压缩、传输以及显示实时同步,并与实际地图结合。从图4可以看出,对应回波有船只、岛屿、建筑物等,很好地反映了实际的情况,从而也说明达到了实时的要求。

5 结束语

本文所涉及到的空间换时间的改进LZW算法是为了更进一步提高压缩的效率,在基本LZW算法的基础上,通过分析哈希函数算法的优缺点,从消耗内存、提高速度的角度提出的。

为了将采集到的雷达数据能进行实时传输并进行实时显示,需要对其进行实时压缩,这就需要压缩比高且压缩速度快的压缩算法。在压缩前对雷达数据进行相关性预处理,可以大大提高压缩比;空间换时间的算法在原有LZW压缩算法的基础上,通过消耗2 MB内存,使压缩速度提高了2～3个数量级,对于压缩效果而言,性能非常好。将该方法运用到实际雷达数据中,实现了数据采集、压缩、传输和显示的实时同步。

该算法实现较简单,且不易出现冲突的情况,性能较稳定,其最大的特点就是通过消耗内存来提高速度。如果压缩的数据很大,建立的字典也随之增大,那么所消耗的内存也会不断增大,这对于FPGA、ARM等嵌入式系统和芯片而言会影响到其他功能的实现,因此对于内存的消耗还有进一步的改进空间,在内存与速度之间要找到一个平衡点,以同时满足两方面要求。

通过对压缩算法的改进,满足了实时传输的要求,为实现雷达实时显示来提供数据,完成对雷达的远程显控功能,实现了雷达数据的入网共享等应用。

[1]徐龙飞.基于FPGA的数据采集系统[D].太原:中北大学,2014.

[2]LI Leiding,MA Tiehua.FPGA-Based Implementation of LZW Algorithm[J].Electronic Measurement Technology,2008,31(10):170-172.

[3]韩慧.一种易于硬件实现的LZW算法的应用[J].电子技术应用,2015,41(2):68-71.

[4]王育民,李晖,梁传甲.信息论与编码理论[M].北京:高等教育出版社,2005.

[5]王智.LZW字典压缩改进算法研究及FPGA硬件实现[D].南京:南京师范大学,2012.

[6]王怀光,张培林,吴定海,等.基于动态LZW与算术编码的缓变信号无损压缩[J].计算机应用研究,2015,32(9):2742-2745.

[7]常传文,茅文深.雷达数据无损压缩研究[J].舰船电子工程,2008,28(4):103-105.

[8]刘林.基于LZW优化算法的雷达数据压缩技术[J].舰船科学技术,2015,37(11):120-123.

[9]TRAPPE W,WASHINGTON L C.Introduction to Cryptography with Coding Theory[M].2nd ed.India:Pearson Education,2006.

[10]冯振.基于LZW的数据压缩硬件系统设计[D].荆州:长江大学,2013.

[11]耿赟,薄保林.实时LZW压缩算法的FPGA实现[J].数字技术与应用,2014(4):135,137.