一种变PRF双基SAR快速极坐标格式算法

丁 晶,李盘虎,毛新华,2

(1.南京航空航天大学电子信息工程学院,江苏南京211106;2.雷达成像与微波光子技术教育部重点实验室(南京航空航天大学),江苏南京211106)

0 引言

双基地合成孔径雷达(SAR)是发射机和接收机分别安装在不同平台上的合成孔径雷达系统。近年来,双基SAR成为雷达领域研究的热点之一。许多高校以及雷达技术研究所都对双基SAR系统进行了研究。2007年,电子科技大学获得了国内第一幅机载双基SAR非同步成像图,其中部分关键技术达到了国际先进水平,这也是国内公开文献中唯一提到并获得的双基SAR实测数据。与国外研究成果相比,国内的双基SAR研究仍然存在一定的差距[1]。

相比于单基SAR,双基SAR无论是成像信号处理还是系统实现都要复杂得多。双基SAR成像目前存在着两个主要的难点,一是距离历程具有双根式性,另一个是成像几何具有三维特性。这两个难点使得基于驻留相位原理的回波信号频谱推导具有很大难度,并且很多单基SAR成像算法无法直接推广应用于双基SAR。尽管如此,科研工作者们还是提出了很多行之有效的成像算法。目前,能够应用于双基移变模式的成像算法主要有卷积反投影算法和极坐标格式算法。卷积反投影算法属于时域算法,计算效率非常低,目前仍然很难达到实时处理。极坐标格式算法是聚束SAR成像的一种经典算法,能够自动补偿载机机动航迹,而且易于与自聚焦算法相结合,因此成为一种很好的双基SAR成像算法[2-3]。

双基SAR极坐标格式算法的处理流程与单基情况下类似。该算法采用平面波前假设,通过重采样将极坐标格式回波数据转换为均匀间隔分布的数据后,进行二维快速傅里叶变换(Fast Fourier Transform,FFT)即可实现成像。极坐标格式算法的实现步骤较为简单,但是需要在空间频率域进行插值运算,空间频域局部的误差会导致图像质量的整体下降,因此该过程对插值算法精度要求很高。而高精度的插值会使得计算效率降低,PFA的应用受到限制[4-5]。针对此问题,单基PFA中分别应用了Chirp-Z变换和PCS代替插值来实现数据重采样。其中,基于PCS的方法效率较高,应用较为方便。对于双基PFA,本文将从信号二维解耦合的角度进一步分析双基SAR极坐标格式插值对目标距离徙动的校正过程,给出双基SAR极坐标格式算法的一种新解释,然后根据该解释提出一种基于变PRF的双基SAR极坐标格式算法,实现提高算法计算效率的目的。

1 对双基SAR极坐标格式算法的一种新解释

1.1 双基SAR信号模型

双基聚束模式合成孔径雷达数据采集空间几何关系如图1所示,地面为xoy平面,成像场景中心点位于坐标系的原点。为了不失一般性,假设发射机和接收机沿任意航迹飞行。发射机与接收机的瞬时方位角和俯仰角分别定义为它们在孔径中心时刻的值分别为接收机接收到的回波信号经解调、脉冲压缩以及运动补偿后可以表示为

式中,c表示电磁波传播速度,fc表示发射信号载频,fτ表示距离向频率,A表示回波信号幅度。根据PFA算法采用的平面波前假设,差分距离ΔR(t)可基于点目标坐标(x0,y0)进行泰勒展开,取其线性项为

式中,rtc(t)和rrc(t)(rt(t),rr(t))分别表示发射机和接收机到场景中心(点目标(x0,y0))的瞬时距离。将式(2)代入式(1),可得回波信号在距离频率域近似:

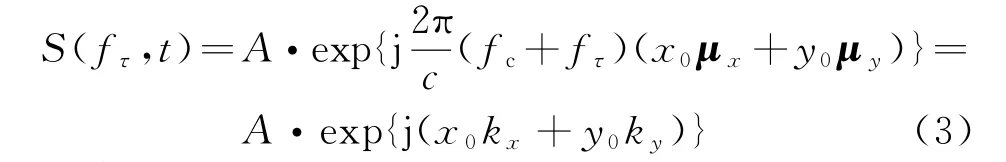
式中,

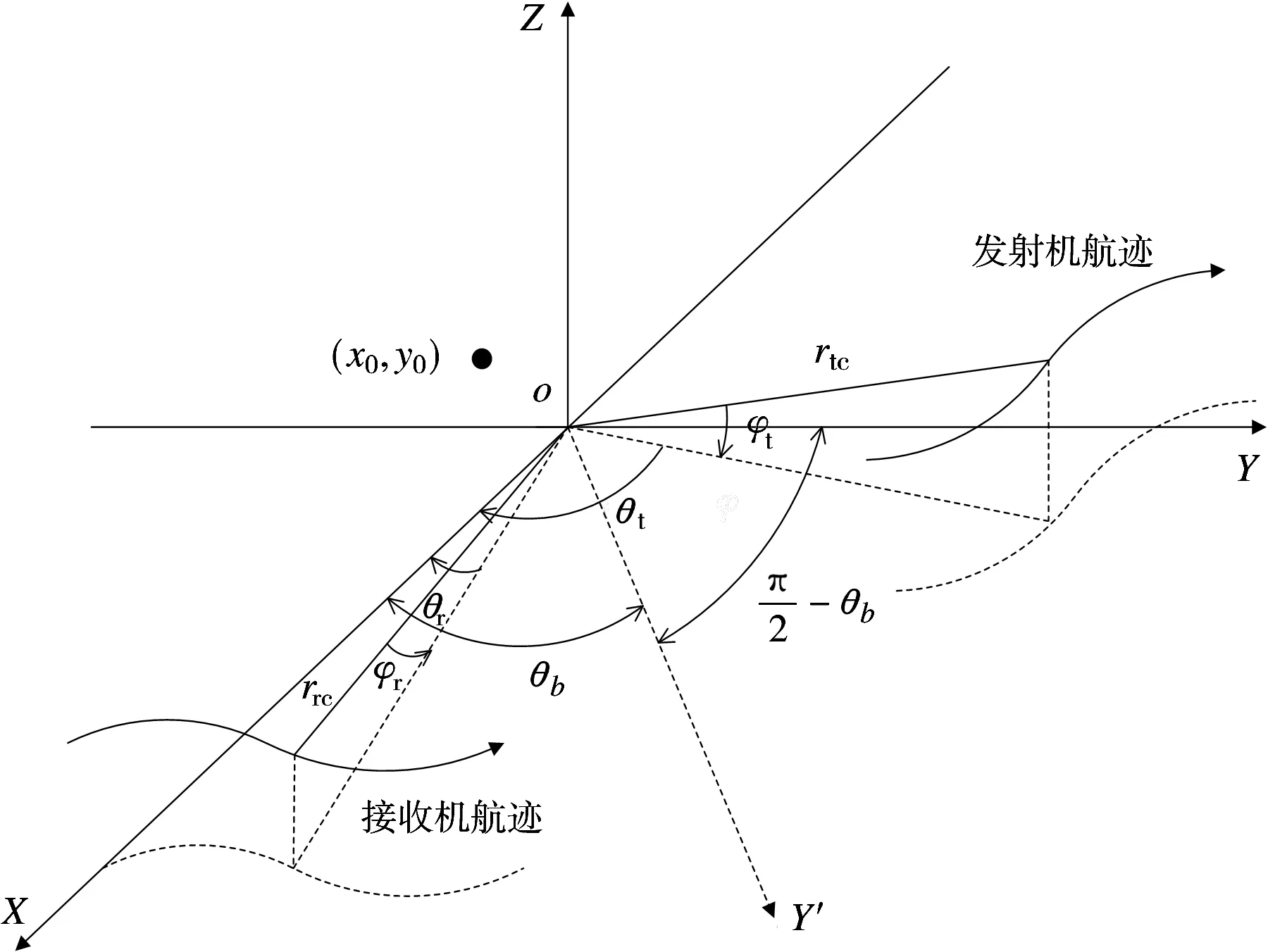
图1 双基SAR数据采集模型

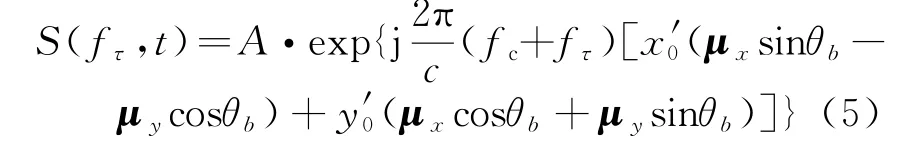
式中,

从式(5)可以看出,回波信号的相位信息包含距离信息和方位信息两个部分,这两个部分方位时间t和距离频率fτ都存在着耦合,这种耦合使得目标存在着距离徙动。PFA通过两维插值实现距离徙动校正即解耦合,其中距离向插值消除目标距离位置项中两变量的耦合,方位向插值消除方位位置项中两变量的耦合。

1.2 距离向插值

距离向插值的目的是消除式(5)中y′0项系数随方位时间t的变化,校正由目标距离位置y′0引起的距离徙动[6]。在数学上,这一过程可以理解为对距离频率作一个变量替换,即令中为新的距离频率变量),使其满足:

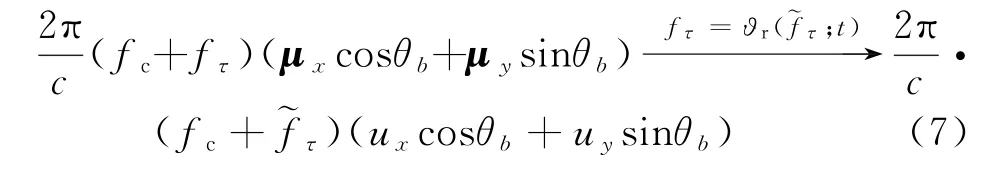
式中,u x和u y分别为μx和μy在孔径中心时刻的值。由式(7)可以得到替换的变量:

由式(9)可以看出,经距离向插值后,距离位置项y′0的系数仅为距离频率的线性函数,与方位时间无关,距离向解耦合完成。

1.3 方位向插值

与距离向插值类似,方位向插值的目的是消除式(9)中x′0项系数随距离频率的变化,校正由目标方位位置x′0引起的线性距离走动、二次及高次距离弯曲[7]。同样,从数学的角度,这一过程可以理解为对方位时间作一个变量替换,即令t=(其中~t为新的方位时间),使其满足

在发射机与接收机的飞行航迹都是任意的情况下,根据式(10)无法得到的解析表达式。因此,将方位向重采样过程分解成如下两步实现:

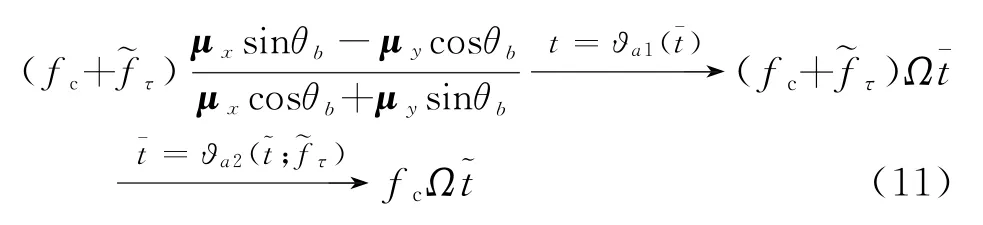
由式(12)可知,方位向第一步重采样消除了方位位置变量引入的二次及高次距离弯曲,仅余线性距离走动。第二步重采样是一个与距离频率有关的方位时间重采样,由式(11)知:

上式表明第二步方位重采样实质上是一个Keystone变换[8],经过Keystone变换后,目标方位位置引起的线性距离走动得到校正,式(12)变为

1.4 两维Fourier变换成像

从式(14)不难看出,经过距离向和方位向重采样后,距离频率和方位时间不再存在耦合,距离徙动得到完全校正,因此再对式(14)作两维傅里叶变换即可实现对目标的聚焦成像,即

式中,F[·]表示两维傅里叶变换,ft表示方位频率,τ表示距离时间,sincr(·)和sinca(·)分别表示距离向和方位向的sinc函数。

2 变PRF双基SAR快速极坐标格式算法

经典的极坐标格式成像算法其实存在着明显的缺陷,在极坐标格式数据到矩形格式数据转换的过程中需要经过两维高精度的插值[9],因为只有插值的精度足够高,最终图像的质量才能得到保障,然而高精度的插值算法又会导致计算效率的下降,因此极坐标格式插值是限制PFA应用的一个主要因素。由上一节对双基SAR极坐标格式算法的一种新解释可知,距离向插值校正了由目标距离位置y0引起的距离徙动,方位向插值校正了目标方位位置x0引入的线性距离走动、二次及高次距离弯曲。方位向插值可以分解为两步进行,第一步是与距离频率无关的重采样,从根本上来说,这一步其实就是对方位时间t进行了非均匀化,校正了由目标方位位置x0引入的二次及高次距离弯曲。由此,本文考虑采用变化的脉冲重复频率,即非均匀采样的方位时间,实现回波信号不存在目标方位位置引入的二次及高次距离弯曲的目的。在采集回波数据后,只需进行距离向解耦合以及方位向Keystone变换便可进行两维傅里叶变换聚焦成像。

2.1 变化的PRF

采用变化的PRF即非均匀采样的方位时间,使得回波数据不存在由方位位置x0引入的二次及高次距离弯曲。由1.3节可知,可以通过线性化来确定非均匀采样的方位时间t,其具体实现过程如图2所示。图中黑色正方形代表假设的均匀采样的方位时间位置,映射到域为非均匀采样,黑色圆点代表非均匀采样的方位时间位置,此时在域为均匀采样。这一过程,在数学上等效于令

由式(5)可知,采用非均匀的方位时间t后,采集的回波信号在经过解调、匹配滤波、运动补偿以及坐标系旋转后可以表示为

由式(17)可知,采用变化的PRF即非均匀采样的方位时间后,回波信号将不存在方位位置x′0引起的二次及高次距离弯曲,故只需再校正距离位置y′0引起的距离徙动和方位位置x′0引起的线性距离走动即可进行两维傅里叶变换实现成像。

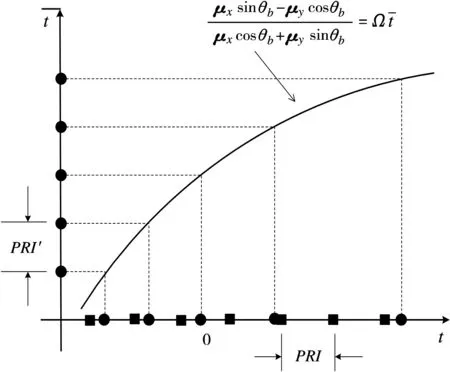
图2 方位时间非均匀化示意图

2.2 距离频率重采样

对距离频率重采样的目的在于校正回波信号中由距离位置y′0引起的距离徙动,等价于在距离向作如下尺度变换:

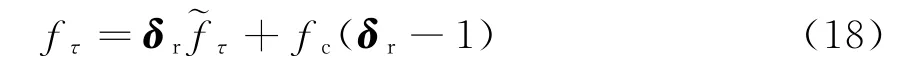
式中,δr=(u xcosθb+u ysinθb)/(μxcosθb+μysinθb)为距离频率变换尺度因子为变换后的距离频率变量。具体的实现过程如图3所示,其中黑色圆点表示原来的距离频率,白色圆点表示重采样后的距离频率。由式(17)可知,对距离频率进行重采样后,回波信号可以表示为

距离频率重采样解除了距离信息部分距离频率与方位时间的耦合,使其仅为距离频率的函数。由式(19)可知,由目标距离位置y′0引起的距离徙动已经得到了校正,只剩下目标方位位置引起的线性距离走动。

图3 距离向重采样示意图

2.3 方位Keystone变换

方位Keystone变换的目的是校正目标方位位置引起的线性距离走动,实际上就是一个与距离频率有关的方位时间重采样,该采样过程可以用以下数学形式表示:

经过Keystone变换后,回波信号可以表示为

从上面的分析可知,变PRF模式可以明显简化后面的信号处理过程,但这一模式也对雷达硬件实现提出了更加严格的要求,目前,美国Sandia实验室开发的雷达已经能够实时进行PRF调整,相信国内也很快能够实现这一技术。因此本文所提方法将会具有较好的应用前景。

3 仿真验证

为了验证上述变PRF双基SAR快速极坐标格式算法的可行性,本节用IDL仿真软件进行了点目标仿真验证。对4个点目标分别运用传统的双基SAR极坐标格式算法和变PRF双基SAR快速极坐标格式算法进行成像。这4个点目标在地面有效成像场景范围内,一个为场景中心O点,另外3个分布于以场景中心O点为圆心,以300 m为半径的圆上,具体位置关系如图4所示。

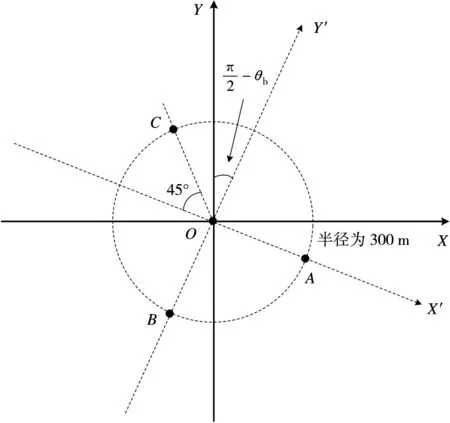
图4 仿真点目标位置关系图

在表1所示仿真参数下,采用传统双基PFA算法和变PRF双基SAR快速极坐标格式算法的仿真结果如图5所示。为了将两种方法的成像结果进行对比,图6～9分别给出了点目标O,A,B,C的两维点目标响应等高线图,可以看到两种方法处理后的点目标响应特性几乎完全一样。

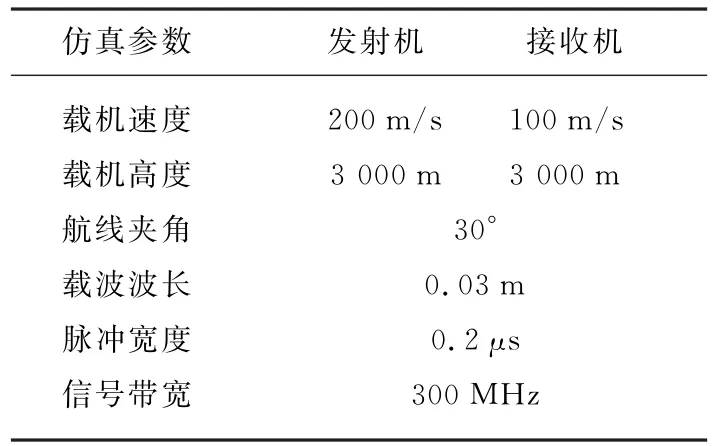
表1 点目标仿真参数

图5 点目标仿真结果图

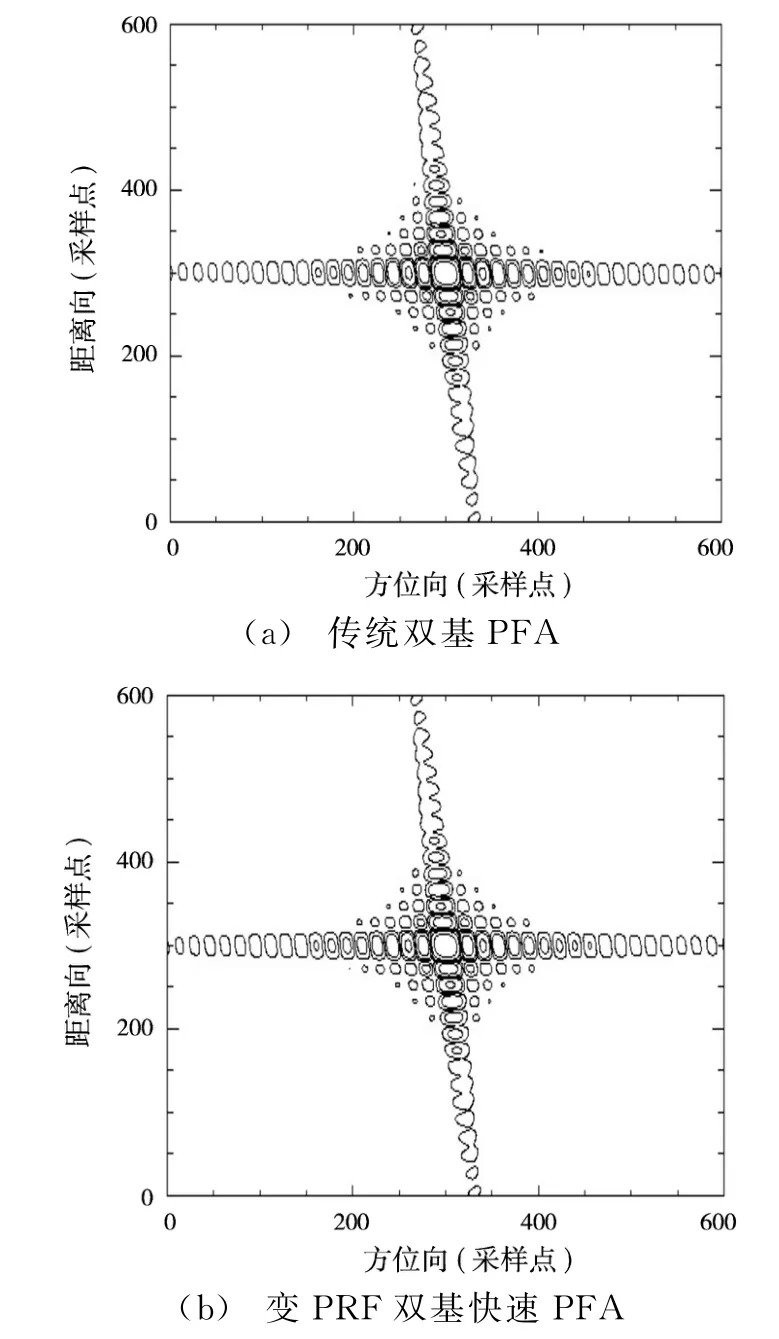
图6 点目标O的两维成像特性

图7 点目标A的两维成像特性

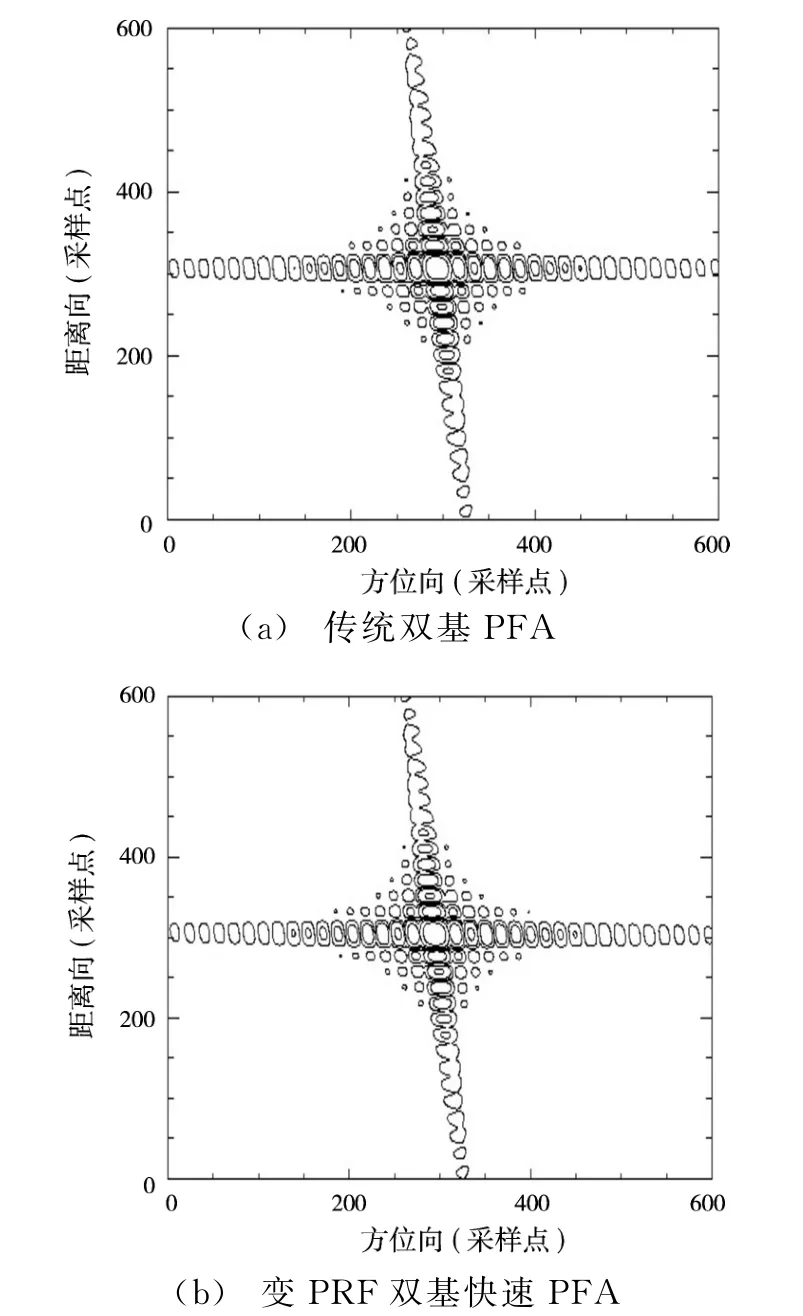
图8 点目标B的两维成像特性

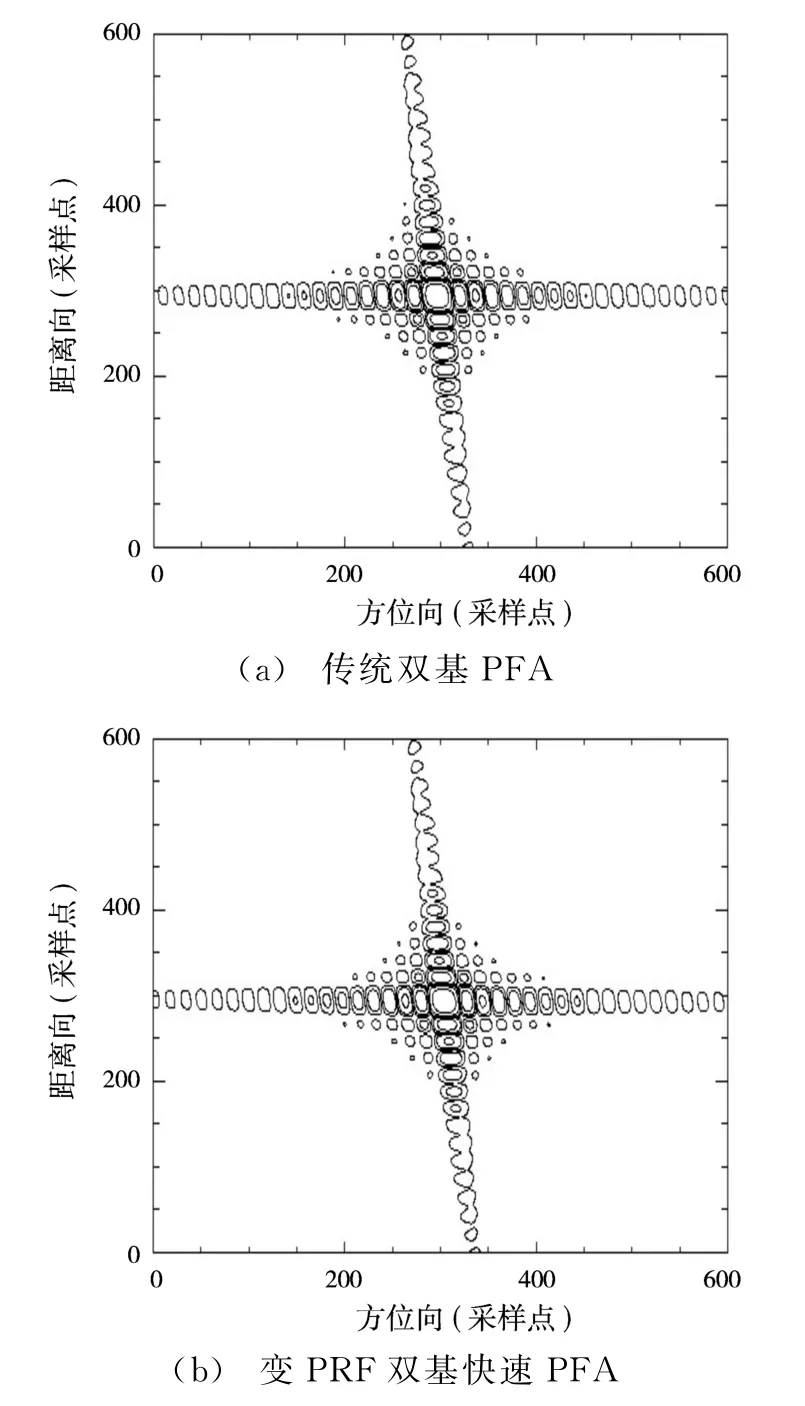
图9 点目标C的两维成像特性

4 结束语

双基SAR极坐标格式算法中距离向插值和方位向插值的本质从距离徙动校正的角度可以理解为回波信号中距离频率和方位时间两个变量的解耦合过程,该解耦合的过程从理论上讲可以用变量替换的方式来实现。本文所提出的变PRF双基SAR快速极坐标格式算法采用变化的PRF,即非均匀采样的方位时间,直接消除方位位置引起的二次及高次距离弯曲,使得采集的回波信号中只存在距离位置引起的距离徙动和方位位置引起的线性距离走动,经距离向重采样和Keystone变换后便可直接进行两维傅里叶变换聚焦成像,一定程度上简化了信号处理的过程,提高了计算效率。点目标仿真验证了该方法的有效性。

[1]SIMPSON R A.Spacecraft Studies of Planetary Surfaces Using Bistatic Radar[J].IEEE Trans on Geoscience and Remote Sensing,1993,31(2):465-482.

[2]王洋,金胜,黄璐.空间目标双基地雷达ISAR成像技术研究[J].雷达科学与技术,2015,13(5):485-489.

[3]WANG Y,BAO Q,WANG D,et al.An Experimental Study of Passive Bistatic Radar Using Uncooperative Radar as a Transmitter[J].IEEE Geoscience and Remote Sensing Letters,2015,12(9):1868-1872.

[4]孙进平,白霞,毛士艺.聚束模式双基地SAR极坐标格式成像算法研究[J].电子学报,2008,36(12):2324-2327.

[5]支双双.双基地雷达两种目标定位方法误差分析与仿真[J].西安工程大学学报,2015(2):209-214.

[6]MAO X,ZHU D,WU D.A New Formulation of Polar Format Algorithm for Bistatic Spotlight SAR[C]∥IEEE Radar Conference,Arlington,VA:IEEE,2015:68-71.

[7]丁金闪,OTMAR L,HOLGER N,等.双基SAR成像的点目标解析频谱研究[J].电子与信息学报,2009,31(4):763-767.

[8]RAINVILLE N.Development of a Real Time Bistatic Radar Receiver Using Signals of Opportunity[D].West Lafayette:Purdue University,2014.

[9]LIN C,WANG D,TIAN R,et al.Target Discrimination Method for Passive Bistatic Radar Using Narrowband and Low-Frequency Illuminator[J].Journal of Applied Remote Sensing,2015,9(1):1-7.