光子晶体能带特性的理论算法和数值模拟

光子晶体能带特性的理论算法和数值模拟

韦德泉

(枣庄学院光电工程学院，山东枣庄277160)

[摘要]基于Maxwell方程研究光子晶体能带结构的理论算法，推导了计算光子晶体能带的时域有限差分方法，传输矩阵法和平面波展开方法，以二维光子晶体为例进行了数值模拟，得到了其能带结构，研究结论对于光子晶体的理论算法具有参考意义.

[关键词]光子晶体;能带特性;理论算法;数值模拟[收稿日期]2015-08-03

[基金项目]国家自然科学

[作者简介]韦德泉(1964-)，男，山东枣庄人，枣庄学院光电工程学院教授，主要从事光学方面的研究.

[中图分类号]04-33 [文献标识码]A

0引言

光子晶体的概念自1987年被S.John和E.Yablonovitch[1,2]提出来之后，光子晶体的研究就成为一个热点，光子能带是光子晶体的一个重要研究方向，通过人为设计光子晶体结构，可以得到电磁波在其中的传播的能带结构，在能带中的电磁波损耗小具有非常好的传输性能，可以按照人为设计的结构传输，因此可以利用这个特性设计滤波器等器件.在设计过程中追求宽的能带结构，达到光子晶体器件设计性能越好.光子晶体能带的计算方法主要有时域有限差分方法[3]，传输矩阵法[4]，平面波展开方法[5]等,按照结构分光子晶体有一维、二维和三维光子晶体，一般可以用传输矩阵法计算一维光子晶体，平面波展开法计算二维光子晶体，时域有限差分法计算三维光子晶体[6-14].本文就光子晶体能带特性的几种理论算法进行研究.

1理论算法

电磁波在光子晶体中传播的理论可以用Maxwell方程精确描述，其方程表示为公式(1)(2)

(1)

▽·[ε0ε(r)E]=0 ,▽·[μ0μ(r)H]=0

(2)

公式(1)(2)没有考虑自由电荷电流，对公式(1)(2)用傅立叶转换到(K,ω)域得到如下的公式(3)(4).

K×H=-ε0ε(r)ωE，K×E=μ0μ(r)ωH

(3)

K·[ε0ε(r)E]=0，K·[μ0μ(r)H]=0

(4)

基于上面的Maxwell方程推导研究计算光子晶体能带的几种方法.

1.1时域有限差分法

1966年K.S.Yee提出了计算电磁场的时域有限差分法.它的基本思想是将空间电磁场的离散单元用Yee元胞表示，即将空间电磁场分成很多网格单元(Δx,Δy,Δz)，就是Yee的差分格式，电磁场E、H分量可分解为四个H或E场分量，将Mexwell方程转化成差分方程求解电磁场特性.这种算法的优点是解具有精确性、收敛性和稳定性.E、H分量方程如公式(5)-(10)所示.

(5)

(6)

(7)

(8)

(9)

(10)

公式(5)至(10)中△t为时间间隔， n为时间步长.在FDTD算法中，稳定性要求是

(11)

计算公式(5)～(10)式，利用边界条件求出时域场，将其转化到频率域中求得本征频率，从而得到光子晶体的能带结构.

1.2传输矩阵法

传输矩阵法的求解思想是将Mexwell方程组化成传输矩阵形式，最后求解本征值问题.利用这个思想将公式(1)，(2)的Maxwell方程化为：

(12)

(13)

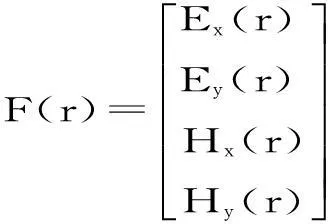
(14)

则下一层的电磁场为

F(r+c)=M(r)F(r)

(15)

根据Bloch定理：

(16)

得到

M(r)F(r)=exp(ik2c)F(r)

(17)

不同的ω可以解的不同的本征值，从而对应不同的波矢量,就得到了光子晶体的能带结构.

1.3平面波展开法

平面波展开法的基本思想是应用Bloch定理，对Maxwell方程进行Fourier变换，将电磁波能带计算问题转化为求解代数本征值的问题.忽略电荷和电流，Maxwell方程可表示如下：

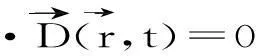
(18)

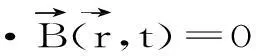
(19)

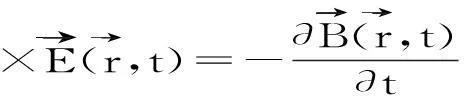
(20)

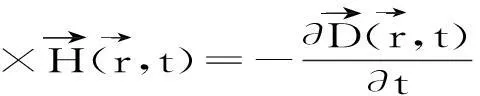
(21)

将公式(18)-(21)的解写成谐振波的形式：

(22)

(23)

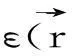
(24)

(25)

将公式(22)～(25)式带入Maxwell方程式得到

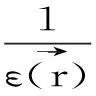
(26)

(27)

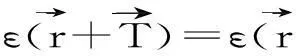
(28)

(29)

(30)

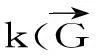
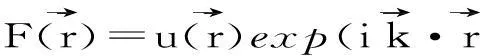
(31)

(32)

将(28)，(29)，(30)代入(26)和(27)并加以整理得到

(33)

(34)

2能带计算

2.1一维光子晶体能带计算

一维光子晶体的模型如图1所示，图中由两层结构组成，介电常数为1和13，应用传输矩阵法计算得到一维光子晶体的能带结构图.图2是一维光子晶体TE模能带结构图，从图2中可以看到出现三个能带结构，带隙范围为0.1452-0.2541He，0.3527-0.5057He，0.5888-0.7340He.图3是一维光子晶体TM模能带结构图，从图3中可以看到出现三个能带结构.图4是一维光子晶体TE/TM模能带结构图，从图4中可以看到出现三个能带结构.

图1　一维光子晶体模型　　　　　图2　一维光子晶体TE模能带结构

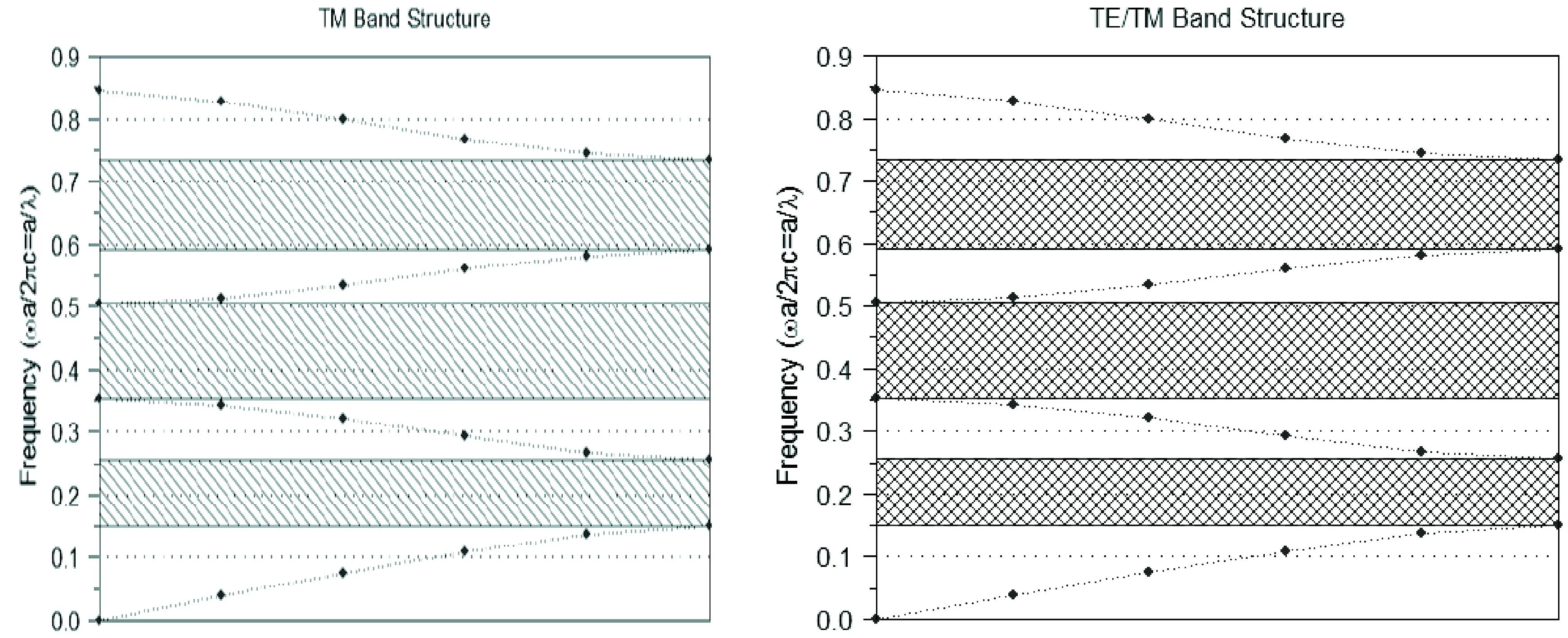
图3　一维光子晶体TM模能带结构　　图4　一维光子晶体TE/TM模能带结构

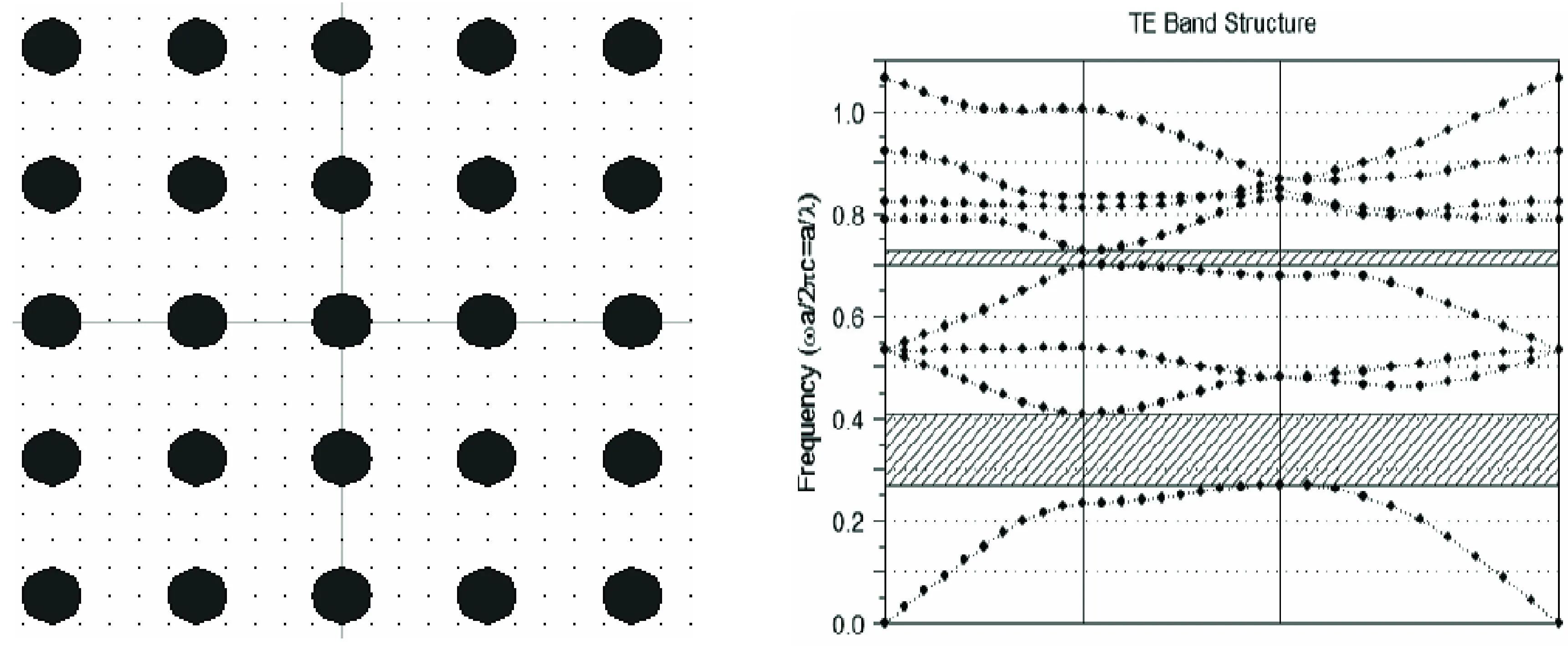
图5　二维正方光子晶体模型　　　　图6　二维光子晶体TE模能带结构

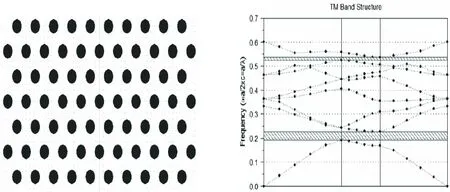
图7　二维三角光子晶体模型　　　图8　二维三角光子晶体TE模能带结构

2.2二维光子晶体能带结构计算

二维光子晶体的模型如图5所示，图中介电常数为1和13的两种材料组成，黑色圆柱介电常数是13，周围是空气，结构成正方形排列，称这种结构为正方晶格二维光子晶体结构.应用平面波展开法计算得到二维光子晶体的能带结构图.图6是二维光子晶体TE模能带结构图，从图6中可以看到出现两个能带结构，较宽带隙范围为0.2726-0.4089He.图7成三角排列，称为三角晶格光子晶体，在图8中可以看到是TM模能带结构，出现两个能带，其中较宽的能带为0.1937-0.2279Hz.

2.3三维光子晶体能带结构计算

三维光子晶体的模型如图9所示，图中介电常数为1和13的两种材料组成，黑色圆柱介电常数是13，周围是空气，图9结构为金刚石三维光子晶体结构，应用时域有限差分法计算得到三维光子晶体的能带结构图，图10是其能带结构图，从图10中可以看到出现一个能带结构，带隙范围为0.4954-0.6355He.图11结构为蛋白石三维光子晶体结构，图12是应用时域有限差分法计算得到的能带结构图，从图12中可以看到出现一个能带结构，带隙范围为0.7827-0.8125He.图13结构为木堆三维光子晶体结构，图14是应用时域有限差分法计算得到的能带结构图，从图14中可以看到出现一个能带结构，带隙范围为0.3406-0.4288He.

图9　三维金刚石结构光子晶体模型　　图10　三维金刚石结构光子晶体能带结构

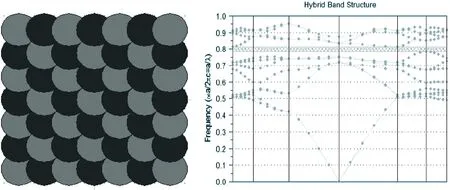
图11　三维蛋白石结构光子晶体模型　　图12　三维蛋白石结构光子晶体能带结构

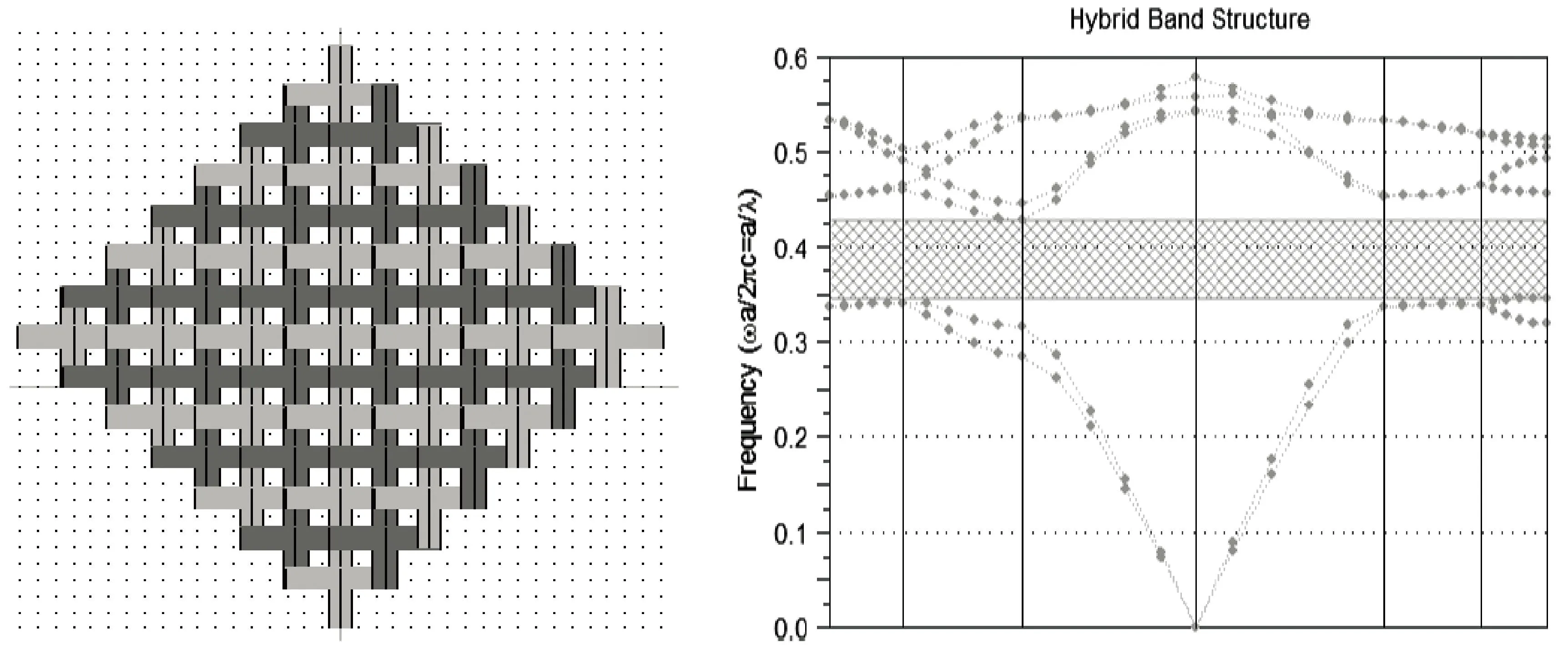
图13　三维木堆结构光子晶体模型　　图14　三维木堆结构光子晶体能带结构

3结论

总结推导了计算光子晶体的三种方法传输矩阵法、平面波展开法和时域有限差分法，并分别用传输矩阵法计算了一维光子晶体的能带结构，用平面波展开法计算了二维正方晶格、三角晶格的能带结构，用时域有限差分法计算了三维金刚石结构、蛋白石结构和木堆结构光子晶体的能带结构.研究结论对于光子晶体的算法以及数值模拟提供参考.

参考文献

[1]John S .Strong locali Zation of Photons in certain disordered dielectric superlattices[J].Physical Review Letter,1987,58(23)：2486-2488.

[2]Yablonvitch E.Inhibited Spontaneous Emission in Solid-State Physics and Electronics[J].Physical Review Letter,1987,58(20)：2059-2061.

[3]I. S. Maksymov，G.I .Churyumov. Photonic Green’s functions calculation by using FDTD method [J].Mathematical Method in Electromagteic Theroy，Interilational Conference on MMET’02,2002,1：201-203.

[4]J.B.Pendry,A.MacKinnon.Calculation of Photon dispersion Relation [J]. Physical Review Letter,1992,69(9)：2772-2775.

[5]H .Miguez，A. Blanco，C. Lopez. Face centered cubic Photonic bandgap materials based on Opal-semiconductor composites[J].Journal of Lightwave Technology，1999,17(11)：1975-1981.

[6]陈淑瑜,韦德泉.三角晶格光子晶体第一带隙特性研究[J].枣庄学院学报,2014：31(5)：47-50.

[7]陈淑瑜,韦德泉.一维光子晶格透射率的数值模拟[J].激光杂志,2014：35(10)：27-28.

[8]H.-T.Chen, J.F.O’Hara,A.J.Taylor,et al...Complementary planar terahertz metamaterials[J].Opt.Express 2007,15(3)：1084-1095.

[9]Hou-Tong Chen, Willie J.Padilla, Richard D.Areritt, et al.. Electromagnetic Metamaterials for Terahertz Applications [J].Terahertz Science and Technology, 2008,1(1)：42-50.

[10]W. J. Padilla, A. J. Taylor, C. Highstrete,et al.. Dynamical electric and magnetic metamaterial response at terahertz frequencies[J].Phys.Rev.Lett.2006,96(10)：107401-1-3.

[11]H.-T. Chen, W. J. Padilla, J. M. O. Zide, et al, Active metamaterial terahertz devices[J].Nature, 2006,444(05343)： 597-600.

[12]X.H.Wang,B.Y.Gu,R.Z.Wang.Numerical method of Brillouin zone integrals of vectorial fields in photonic crystals[J].Phys.Lett.A,2003,308(2)：116-119.

[13]R.Z.Wang,X.H.Wang,B.Y.Gu et al..Local desity of states in three-dimensional photonic crystals：Calculation and enhancement effects[J].phys,Rev.B,2003,67(15)：1551141-1551147.

[14]Amit Agrawal, Ajay Nahata.Coupling terahertz radiation onto a metal wire using a subwavelength coasxial aperture[J].Optics Express, 2007,15(14)： 9022-9028.

[15]Charles.Kittel,Introduction to Solid State Physics (Wiley, 1996).

[责任编辑：闫昕]

Theoretical Algorithm and Numerical Simulation of Bandgap Properties

for the Photonic Band Gap Photonic Crystal

WEI De-quan

(Department of Opto-electrical Engineering, Zaozhuang University, Zaozhuang 277160, China)

Abstract：Finite difference time domain method, the transfer matrix method and plane wave expansion method were deduced based on the Maxwell equation theoretical algorithm for the photonic crystal band structure. The band structure of two-dimensional photonic crystals were simulated based on the above these methods. The research conclusion has reference significance for the theoretical algorithm of the photonic crystal.

key words：photonic crystal; bandgap properties; theoretical algorithm; the numerical simulation