协同学，耗散结构理论和超循环论

协同学，耗散结构理论和超循环论

张一方

(云南大学物理系，云南昆明650091)

[摘要]首先讨论协同学及其应用，由此说明生命在于混沌中的协同.其次探讨了耗散结构理论及某些问题，进而研究孤立系统的熵减.最后讨论超循环论，其可以用图论中的连通度定义.此外，提出它们可能的发展方向.

[关键词]协同学;耗散结构理论;超循环论;非线性[收稿日期]2015-08-10

基金项目

[作者简介]张一方(1947-)，男，云南大学物理系教授，主要从事理论物理的研究.

[中图分类号]R338 [文献标识码]A

0引言

已知在广泛应用的横向理论中，系统论、信息论、控制论被称为“老三论”.协同学、耗散结构理论、突变论、混沌、分形、超循环论被称为“新六论”.对这些理论已经存在许多专著.笔者在简要介绍系统论、控制论、信息论、突变论和混沌等五种理论的基础上，提出易拓扑学，探讨了它们与易的关系.同时讨论了其中的某些基本问题，如系统结构动力学，信息和负熵的关系，突变和地震的非线性动力学等.并且总结了这些理论的共同特点和关系[1].基于分形，笔者讨论了分形相对论、推广的Noether定理和时空的新探索[2]，研究了 Higgs机制、强子的质量公式、暗物质和粒子的分形模型[3]，探索了生物学中的分形和混沌[4].进而，笔者提出复数维[5-7]，并且探讨了分形的某些应用，包括应用于社会科学和文学，研究了分形中的若干基本问题，特别是分维、分形中量纲的奇异性，探索了宇观-微观分形、泛量子理论和对分形的展望[8].笔者引入的泛相对论及由此联系于多世界等[9]，其主要数学基础之一就是分形.在此讨论协同学、耗散结构理论、超循环论及其相关的问题和应用，并提出它们可能的发展方向.

1协同学及其应用

哈肯提出的协同学，研究一个由性质完全不同的大量子系统(诸如光子、电子、分子、细胞、器官、生物、人以及各种社会系统)以复杂的方式相互作用所构成的种种复杂系统，在一定条件下，子系统之间按照一些普适规律，通过非线性作用产生相干效应和协同现象，使系统形成有一定功能的空间、时间或者时空、功能的结构.协同学的目的是建立一种用统一的观点去处理复杂系统的概念和方法.它的中心议题是，探索存在于支配生物界和非生物界及一般系统的宏观尺度上的结构、功能的自组织形成过程的某些普遍原理.协同学是一门学科，而自组织是一种现象.这是一种相变的统一性，结构形成过程及其规律的统一性[10-13].

协同学从创立之日起就已被用于众多方面和领域.在数十卷的《Springer协同学丛书》中有最集中的反映.近年哈肯重点研究了复杂系统的典型、新科学的前沿——大脑工作原理[14]和大脑动力学[15].他认为大脑是一个产生活动时空模式的自组织系统，是遵从协同学规律的复杂巨系统，由此在宏观层次建立了脑活动的连贯理论.哈肯及其合作者以手的运动为起点，讨论了运动协调及其相关领域的实验和模型，协同学在其中必然起着基本作用.以行为模式转变为例，手的运动的状态只有两种稳定的位相存在，二者之间的突变发生在临界频率处，突变后只能观察到一种运动模式.进而，我们的身体，一个具有大量自由度的高度复杂的系统，其高度协调的宏观运动可以用单个序参量描述，它支配着整体的运动模式.与其出现紧密相联的是一种经过压缩的容量极低的信息.根据最大信息原理，可以找到合适的序参量.进一步，结合脑电图分析、视觉的方方面面和神经计算机、协同学计算机等，由一个(或几个)序参量可以描述行为，决定宏观模式.而且，他们证明了通过学习，大脑如何减少序参量的数目，并由役使原理(包括循环因果律)在宏观层次和微观层次之间架起桥梁.从而建立了大脑的网络模型，其中存在序参量的等级.在许多情况下，甚至可以求得相应的支配宏观行为的耦合的非线性振荡器方程.

在实验事实的基础上，哈肯用数学方法讨论了神经元和它们间的协作，并具体提出了脑活动的场论，神经网络的灯塔模型和综合-发射模型(Integrate and Fire Model)、相锁、协调等，及相应的各种方程.深入的研究揭示出，大脑动力学可以归结为极大简化后的序参量动力学，由低维系统的方程支配.它的行为可以化为求解微分方程，由具有能产生空间和时间的高度相干现象，决定整个神经系统的属性.这将有助于建立认知过程的动力学，进而破译精神与物质，这个永恒的难题.

基于大脑神经网络巨系统的功能特点和知觉及思维的产生是大脑复杂的神经网络巨系统中各子系统的协同综合作用的结果，我们提出大脑协同学及相应的某些基本原理和方法[16,17].并且由协同学的基本方程定量导出Lorenz方程和Lorenz模型，其中的两翼对应于大脑的两个半球，两翼之间的跳来跳去形象地描述思维.由此说明生命在于混沌中的协同.大脑协同学具有三个层次：大脑的结构、活动和思维，及进一步把气功作为一种心身协同学[18].人体协同，大脑是指挥.

我们定量分析了种群动力学及生物-生态协同学[19,20].并由Lorenz模型可以描述两种种群的变化关系.当取绝热近似时，还可以导致种群动力学的不同模型，并指出保护濒危物种的两条出路.因此，生物协同学能够深刻揭示不同物种之间，既竞争又协同的复杂的非线性关系.

协同学的基本方程之一是Langevin方程[10]

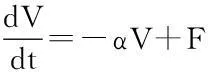
(1)

它是具有阻尼，又有随机力的一阶微分方程.其解为

(2)

最后一项随时衰减.方程可以发展为

(3)

其中右边一、二项决定总的演化方向，如对经济、舆论等，Kif有导向作用，确定增或减；J(f)是非线性项，可以导致孤子、混沌等；F(t)是随机项，能引起涨落，导致相变.概率分布变化的Fokker-Planck(FP)方程为

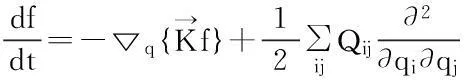
(4)

这既能描述决定论性的过程，也能描述随机过程.它的定态解可以导致Langevin方程(1)，变化形式后可以作为连续性方程.由守恒定律、连续性方程也可导出FP方程.

一般非线性方程的关键是控制参量(序参量)，其在不同区域是1，2，4，…2n周期和混沌.三个量协同可用激光方程[10].二个量协同可用生态互惠方程[21,22].协同学方程可以化为Lorenz方程，因此具有其各种特征.由此可以描述大脑的形成和功能，肺的形成，舆论聚焦于两种[23]等各种对称结构的形成.这就是由协同、混沌产生对称.

物理方面，协同学可以联系于半导体和脉冲现象，导出单峰.进而可用于统计物理、冷聚变[24]、化学、天文、地学、生物、生态、生命、经济、管理、结构、哲学、宗教、美学等方方面面.可结合各种非线性理论和三维、多维哲学.

协同学研究整体性、整体运动、整体状态.广义协同学还应该研究结构解体，熵极大，混沌，序参量向相反方向变化等相反或更深的领域.耗散结构、混沌和超循环可以认为是广义协同学的三种结构.

更一般，任意两个(多个)相关系统的强或弱协同学.基本原则是协同，但协同学已经包括竞争.具体原则是竞争中1).多数为主原则，仅有小涨落；2).力度原则.二者结合导致伺服原理.激光方程和各种可用于种、群的方法都可用于此及人-自然协同学[25]，可以讨论其双螺旋结构及相应的方程组.

协同学中对生物促进生长的激素和阻止生长的抑素，类似阴阳学说.协同学可以成为老庄哲学、易经、中医、气功及互助论等和谐、统一哲学的数理基础.心身协同[17]，人与自然协同[25]，对应天人合一.协同学应该联系于佛、道等各种宗教.

心-身协同学[17]、人-自然协同学[25]推广为人与时间、空间、环境协同学[20].协同学使日地变化的地壳运动、地磁场变化、地球自转、太阳黑子、气候变化、地震等六大周期彼此相关.由协同学得到Lotka-Volterra(LV)等非线性方程组，导致黑子等各种周期.进一步建立各种周期的泛理论.Lotka-Volterra模型及其发展是：

(5)

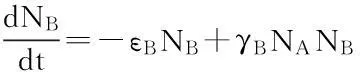
(6)

这是保守的非线性系统，其中有三个因素，会出现振荡周期.

1997年，哈肯对协同学作了简明扼要的总结，并讨论了系统论、控制论、信息论、耗散结构理论、协同学及自组织、行为和认知等之间的关系.由于协同学研究的是一般规律，因此与它的应用的广泛性相一致，而和诸多的领域关系密切，使用了其中的各种术语和方法.但是，协同学引人了与每个专门领域不同的特征、概念和方法.它研究的是一种普遍的动力学行为，其中的变化具有十分丰富的多样性.虽然协同学和系统论都探索支配系统行为的一般原理，但它的目标明确地集中于系统的宏观性质经历显著变化的情况.在协同学中，信息论是一种基础，一种工具.协同学用了控制论的概念，然而目的是为了研究在控制作用下系统的变化、结构的形成和自组织行为.协同学和耗散结构理论都研究远离平衡的状态和非平衡相变，但是协同学研究的范围要广泛得多，不仅包括稳定的时空结构，而且包括各种振荡、混沌和十分广义的相变.因为协同学研究相变，所以它必然可以应用突变论的某些方法和结果，但二者的数学方程都有很大差别.又因为协同学本质上是一种非线性理论，所以它可以导出混沌.由于协同学和各种新兴科学密切相关，所以它具有新颖性.它又和众多理论广泛联系，所以具有综合性.此外，由于它所建立的基础的特点，所以具有明显的数学化、定量化特征.协同学可以被看作最先进的自组织理论.

协同学作为一门新兴科学，已经取得了举世瞩目的成绩.但是，它还在发展，还有一些问题有待探求，还有广阔领域等待开拓.哈肯就指出下列问题还需要发展：1)一种新型的信息已经出现，它涉及序参量并反映着系统集体性质，而称为“协同学信息”.同时，序参量具有“信息子”的意义.2)在发生分支的情况下，如何构造随机过程的势函数.这对生物的进化或者发育都有根本性的重要意义.而且，这样一种函数是否真正存在，仍然是一个没有解决的问题.3)应用什么样的控制参量可以使系统得到一个所需要的新状态，即用控制参量的方法影响系统的行为，使其自组织形成理想的结构.4)协同学进一步应用的一个广阔领域是网络，它可以发生在一切大小不同的水平上，可以是在人之间、机器之间以及人机之间.如何控制它们，教导它们，如何寻找一个支配着网络程序的适当的序参量.用各种复杂的网络模拟不同的生物系统，由此认识血液循环、呼吸系统、甚至大脑的功能.此外，协同学还可以更深入地应用于生物系统、经济领域和城市计划等方面.

协同学正在发展，并不断开拓自己的研究领域，甚至用于中医学和瑜伽术等，因此可以预言它将应用于更广阔的天地.

更一般说，协同学力图揭示自然界变化和结构的更本质的规律，实现自然界在各个层次、各个方面的统一，并进而达到自然科学和社会科学的统一，所以它的目标是远大的，也是艰巨的.但是，正因为协同学可以广泛应用，可以继续发展，它才是大有希望的.

2耗散结构理论和孤立系统中的熵减

耗散结构研究开放系统，其具有三个共同特性：存在于开放系统中，保持远离平衡态的条件，系统内各要素之间存在非线性相互作用[26-29].局部非平衡通过统计平均化为整体的平衡.I.Prigogine用局域平衡假定把很多概念(如熵)、方法等推广到整体非平衡态.他认为复杂系统必须用Liouville方程，推广Liouville方程，有扩散项时导致时间不可逆.

耗散结构，其形成在物理方面是一个非平衡的相转变；其理论在数学方面联系于非线性数学，Markov过程可以提供一定的数学工具.Prigogine指出耗散结构三个互相关联的方面，“功能⟺结构⟺涨落之间的相互作用，是理解社会结构及进化的基础.”这基于系统的划分，所以又联系于系统论.

Prigogine系统讨论了混沌生序(OrderoutofChaos)[27].一切系统都含有不断“起伏”着的子系统.当这种涨落在某种条件下被放大时，原有的结构就会被破坏.并且在某个奇异时刻(相应于分支点)，系统可能化为混沌状态，或跃迁到新的结构.这种变化是在远离平衡的状态，与非线性过程结合.由于非线性相互作用，结果出现多样性.涨落导致有序.

由偶然性决定分支点后系统的下一步状态.这是偶然性和必然性的综合.“仅当一个系统的行为具有足够的随机性时才可能区分过去和未来”，才导致不可逆性.Prigogine指出：“有序和无序总是同时出现的，这可能就是生命出现的规则，也可能是宇宙创立的规则.”耗散结构理论是研究向有序转化的机理、条件和规律.这是非平衡系统的自组织理论.远离平衡的稳定态是一种开放的有序结构.它可以统一生命和非生命科学.

我们处于一个存在多种涨落的世界，有些涨落导致进化，有些涨落导致退化.这些涨落是不稳定的动力学系统在微观层次上产生的涨落在宏观层次的表现.对于开放系统，可能进入的是增加有序度的负熵流，也可能是增加无序度的正熵流.远离平衡可能是有序、发展，也可能是无序、衰亡.只有当开放系统的熵流deS<0，才能降低熵值，在系统中形成结构，并保持下去.对此，我们定量论证了虽然负熵流的引人可以使系统的熵减少，但由于熵产生Si和总熵S必须为正.

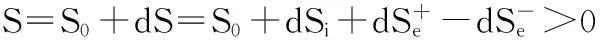
(7)

(8)

即负熵的绝对值大于零，但不能使总熵为负值.这就是任何开放系统输入负熵流的适度性的定量范围.并且开放系统还可能流入正熵[30].

进一步，笔者于1994和1997年分别在国内外提出，热力学第二定律建立在统计独立性等基础上，因此孤立系统中存在熵减的可能性，其必要条件是孤立系统中的子系统间存在涨落和内部相互作用，特别对于吸引过程、内能、系统熵和非线性相互作用等时[31-33].此时熵就不是可加的广延量，由此笔者提出孤立系统总熵变化的推广公式是[33]:

dS=dSa+dSi,

(9)

其中孤立系统内部熵的可加部分是恒为正的dSa；而dSi是相互作用部分，可正可负.(9)式类似Prigogine耗散结构理论中的著名公式：

dS=diS+deS.

(10)

它们分别用于系统内部和外部存在相互作用时.这样就可能形成熵较低的自组织结构.(9)和(7)结合，则熵的总变化公式是[34]：

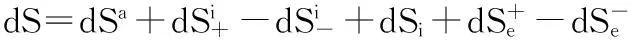
(11)

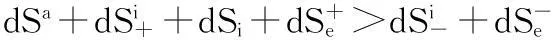
(12)

熵增dS>0，系统趋于无序.当

(13)

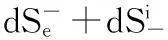
我们的这一研究不仅和系统论、协同学等是一致的，而且在自然科学[34-36]和社会科学[37,38]的很多领域中都存在这种可能性.现在它已被列为中国《21世纪100个交叉科学难题》[39].此外，热力学中的负温度与通常温度的意义及物理和数学的某些基本概念是完全矛盾的，它必然导致熵减[35].最近，Shokef等研究了对能量守恒非平衡定态的一个可解模型，接触的两个系统并不达到相同的有效温度，与这一操作温度相联的系统总熵可以减小[40].Erez等则讨论了用量子测量控制热力学，并且发现相应于系统和热浴二者的熵和温度增加或减少仅决定于观测率，这与标准的热力学规则相反[41].由此可知，对热力学第二定律普适性的质疑已经开始再次成为令全世界科学家关注的问题.

Prigogine指出，在量子力学中存在一种二元性：一方面是时间可逆的薛定谔方程，另一方面则是波函数的坍缩.因此，量子理论是不完备的，必须进行根本性的修正.实际上，在持续的相互作用中，扩散项变成支配项.任何测量已经暗示着一个不可逆过程，而测量仪器提供了时间对称性的破缺.结合不可逆性，动力学定律具有了新的含义，它们不再表达确定性，而是表达概率性.在新的表述中，概率是自然法则的结果，是一个基本量.

Prigogine还指出，目前的科学要么用个体描述，要么用统计描述，对简单的稳定系统，个体观点(就轨道而言)和统计观点(就概率而言)是等价的.但是不稳定性和不可积性，在所有层次上都打破了这两种描述之间的等价性.它使概率获得了一个内在的动力学意义.由此导出一种新型的Prigogine提倡的群体动力学.它联系着被Poincare证明的动力学系统基本上是不可积的观念，并且把不可积性作为动力学的新起点.其中由共振以及由充分发展的混沌，在经典力学中就可以精确导致扩散，从而引入不确定性，形成一个产生熵的不可逆过程，并达到时间对称性的破缺.

Prigogine提出对于物质状态而言，相变在单个粒子的层次上毫无意义，只有在群体层次上才有意义.持续的相互作用意味着我们不能把系统的一部分取出来，孤立地加以考虑.正是在这种群体和全局的层次上，过去和未来之间的对称性被打破了，由此科学中可以引入时间流.而在宏观物理学中，不可逆性和概率是最明显不过的.同时，不稳定性也要求推广经典力学.并且他具体应用Perron-Frobenius算符的统计描述方法，由轨道层次上的不稳定性导致统计层次上的稳定性，从而打破个体观点与统计描述之间的等价性.Prigogine不仅提出混沌定律，认为混沌问题不能在个体轨道层次上解决，但可以在系综层次上解决.他还提出一个基本的创新思想：对于不稳定的动力学系统必须走出Hilbert空间.这与需要整体的非局域描述的持续相互作用有关.只有在Hilbert空间之外，个体描述和统计描述之间的等价性才会被无可挽回地打破，不可逆性才能结合到自然法则之中.

Prigogine提出[26]：量子力学中有坐标和动量的互补性，我们也应该有动力学描述和热力学描述的互补性.以后，他对不稳定系统动力学深入研究以后，进而提出应该在统计层次上重新表述动力学，并断言这将导致经典力学和量子力学的扩展.当然，动力学的不稳定性只是提供产生自然演化模式的必要条件.一旦我们完成了统计描述，就能表述复杂性，例如在宏观层次上的耗散结构，所需要的附加因素.由此可以认识各种结构、自组织和生命出现等复杂性的十分重要的动力学根源.我们必须依据我们置身其中的开放的演化的宇宙来修正物理学定律的表述.

Prigogine认为，探讨耗散结构及更一般地认识复杂性的动力学起源，是当代科学最引人入胜的基本难题之一.我们的兴趣正在从“实体”转变到“关系”，转变到“信息”，转变到“时间”上.由此他提出一个以时间为序的关联流，并在计算机模拟中得到证实，从而发展为关联动力学.

一般地说，在我们的世界里，在所有层次都存在涨落、分岔和不稳定性，由这些不确定性将产生时间之矢，并导致大自然的统一性、多样性和复杂性.我们的世界是一个充满涨落的、嘈杂的、混沌的世界，但也是一个生机勃勃、丰富多彩的世界.

Prigogine坚信，科学的发展正处于一个重要的转折点.著名的未来学家托夫勒认为，Prigogine的思想是改变科学本身的一个杠杆，是迫使我们重新考虑科学的目标、方法、认识论、世界观的一个杠杆，也将是当今科学的历史性转折的一个标志，是最近一次科学革命的中心.它使科学面对一个更现实的、不稳定的、非平衡的、动荡的世界，它帮助我们创造一种崭新的秩序.Prigogine还提出过一个大胆的充满哲学意味的命题：“时间先于存在(timeprecedesexistence)”.他从大爆炸理论和宇宙起源开始，一直讨论到真空中能量守恒的涨落、广义相对论和宇宙学原理等.他认为宇宙的出现与引力场的量子涨落相联系.我们的宇宙在创生之前就存在时间之矢，并且这个时间箭头将永远继续.时间的起源问题也许将永远伴随着我们，但它可能没有开端.

耗散结构理论目前形式的问题有：1)系统应该只分为两类，因为能量和质量是统一的.2)贝纳特花样就是只有能量交换而无物质交换的耗散结构.推广到社会科学等，交换的应当包括既非物质又非能量的信息.3)远离不明确，什么条件下出现等，仍然是不定量.耗散结构理论主要指出一种可能性，但定量化不够.理论一具体化就成为布鲁塞尔振子，或分岔-混沌理论等.高维耗散系统δ,α与一维不可逆映象的结果一样.保守系统的δ=8.721… α=4.02…一维拓扑熵可以定量计算单因素，如时间的社会科学.以后推广到有限维，和有限起伏(涨落).

熵可用于探讨环境、资源、信息化社会等问题.确定各个领域，各个部门的熵、负熵、信息、能量、自由能等.耗散结构、负熵结合信息论、控制论，研究有序和广义进化.这应该是泛熵.

Prigogine等认为耗散结构、演化趋于稳定态[27,28]：Planck所说，自然偏爱某些态.而经典力学则相反，它对应于吸引子.这在物理上是广义惯性原理、最小作用原理等.但是经典力学演化结果可知，而非线性结果无法预言，当然更无稳定态.这是一个巨大的矛盾！可能两方面都存在，而且可以有更大的统一.数学上应该统一为极限环、奇点等.趋于极限环是演化，达到极限环是守恒.而守恒系统，轨道完全由初值决定.

Prigogine有一个雄心勃勃的宏伟理想，试图把科学活动合并到社会之中，试图把二者统一起来，试图在新的观念上实现它们的综合.这个理想是伟大的，也是艰巨的.这是一个兼备哲学家和科学家素质的人，才可能具有的追求.这是在所有时代，一切伟大的人始终追寻的美好的梦.

3超循环论及其可能的发展方向

1960年由Ross Ashby提出超稳定性，描述在达到平衡之前系统对环境的逐级适应.以后，艾根(Manfred Eigen)提出著名的超循环论，这是依靠其自身内部因素进行自我调节、自我组织，而形成的一种有序机制[42].它是一种复杂系统产生生命等自组织结构，并不断演化的重要理论和方法，是一种大循环中包含小循环的定量化的理论.

超循环提出循环的等级组织，信息和功能互为因果.多样性的生物，其细胞又只有一种基本的分子机构，即普适的遗传密码，基本一致的翻译机构和一种大分子手性.这是统一性.系统中有竞争，也有协同，出现非线性选择行为，产生超循环组织.分子自组织，超循环应该是一个非平衡熵减过程，应该发展相应的非线性方程.其由化学反应出发，而不能是孤立系统.互相催化的超循环又类似粒子物理中互相组成的靴带(bootstrap)模型.复杂的Feynman图可以类似超循环，二者可以类比发展.

典型的超循环对应于对称性(群、置换群、旋转群)；但一般的超循环则不是完全对称的，而具有对称破缺.对此引入熵流、能流.超循环理论的数学发展方向之一应是极限环结合非标准分析(NSA)，可称NSA的极限环，其中又有放大后为环的点.可能联系于量子引力环理论、肺模型和非线性整体生物学[43].超循环是一种组成日益复杂的拓扑结构.

其实整个生态系统就是一个多级超循环.单个物种循环(繁殖)，n个相关物种循环.如同一株大树发展到同一局部区域，再发展到更大区域和整个区域.叶绿素的合成，人类的发展都应该是超循环.社会发展结构可以归为大的超循环.社会科学中的各种超循环都有良性、恶性二种，如教育、经济、法制、改革等[44].这些都可以用超循环的各种方法研究并发展.

近年Campos等解析地研究了偏向错误的自复制模板的网络形成一个不对称的超循环及其错误尾巴的稳态政体[45].Ferreira和Fontanari解析地研究了住在二维格子中自复制分子的小群体能够坚持的必要条件，这些分子用超循环复制品模拟，从而讨论生命起源模型中的非平衡相变[46].Montina等讨论了非Gauss统计和一个非线性光学空穴中的极端波，并确定由空穴场的非局域耦合得到的超循环类型扩大产生的空间对称破缺机制[47].

最近，笔者基于超循环论的基础、数学和结构，提出超循环论的图论及其矩阵表示，图G=(V,E)，V是点集，E是边集.因此由图论的点连通度k(G)和边连通度λ(G)就可以定义超循环，连通度越大，超循环越高[48].其中某些表示已经涉及图论的推广.并且讨论了超循环论的应用，及其与五行和东方经济学[49,50]等的关系.

在回顾西方经济学的某些不足后，结合东方的思维体系，笔者提出东方经济学及其三个基本原理(阴阳、五行生克原理，三才整体原理，多元循环原理)[49,50].其主要特点是整体、平衡与和谐，其最高境界是天人合一原理，即自然-人-社会和谐原理，进而探讨了相应的数学理论及某些具体应用.东方经济学是一种非线性整体经济学，也是顾及各种因素的多连通拓扑经济学[49,51,52].东方经济学和经济拓扑学密切地联系于超循环论，而中国传统农业和农村中已经存在完全的循环经济[53].目前循环经济是资源→产品→废物→再生资源的三元循环.笔者提出以后发展为五元就可能有生克关系.更具体说，金木水火土可能分别对应工业、生态、商业(水利)、管理(交通)、农业[49].多元循环对应循环经济.其中每一方面又有循环，就组成超循环[42].

总之，超循环推广后可用于各种广义进化和宇宙演化，它由简单向复杂进化[54].道生一、二、三，三(出现相互作用和非线性)生万物.而且，超循环及其发展、应用、泛化等可以在不同层次.

参考文献

[1]张一方.易拓扑学、混沌和五种横向理论的基础研究[J].安阳工学院学报.2012.11(6): 84-88;90.

[2]Chang Yi-Fang. Fractal relativity, generalized Noether’s theorem and new research on space-time[J]. Galilean Electrodynamics. 2010,21(6):112-116.

[3]Chang Yi-Fang. Higgs mechanism, mass formulas of hadrons, dark matter and fractal model of particle[J]. International Journal of Modern Theoretical Physics. 2014,3,1,1-18.

[4]Chang Yi-Fang. Chaos, fractal in biology, biothermodynamics and matrix representation on hypercycle[J]. NeuroQuantology. 2013,11(4):527-536.

[5]张一方.粒子的分形模型,复数维及其意义[J].大自然探索.1988,7(2):21-23.

[6]张一方.数学,物理中分维的发展和分维时空理论[J].大自然探索.1991,10(2):49-54.

[7]Chang Yi-Fang. New tree-field representations in graph theory, extension of Dirac extraction, differential test for series of positive terms, complex dimension and their applications[J]. International Journal of Modern Mathematical Sciences. 2014,9(1):1-12.

[8]张一方.分形的推广、应用和某些基本问题[J].枣庄学院学报.2014.31(5):1-8.

[9]张一方.泛相对论，物理中的各种方向性和多世界[J].枣庄学院学报.2015.32(2):1-8.

[10]H.哈肯,徐锡申等译.协同学导论[M].北京:原子能出版社.1984.

[11]H.哈肯, 郭治安译.高等协同学[M].北京:科学出版社.1989.

[12]H.哈肯,协同学和信息:当前情况和未来展望,喻传赞,彭匡鼎,张一方,黄兆雄编:熵、信息与交叉科学[C].昆明:云南大学出版社.1994.1-42.

[13]H.哈肯,凌复华译.协同学,大自然构成的奥秘[M].上海:上海译文出版社.2001.

[14]H.哈肯,郭治安,吕翎译.大脑工作原理[M].上海：上海科技教育出版社.2000.

[15]H.Haken. Brain Dynamics[J]. Springer. 2002.

[16]张一方,杨全.大脑协同学,Lorenz模型和认知科学[J].商丘师范学院学报.2001,17(6):25-27.

[17]Chang Yi-Fang. Neural synergetics, Lorenz model of brain, soliton-chaos double solutions and physical neurobiology[J]. NeuroQuantology. 2013,11(1):56-62.

[18]张一方,罗新,朱念麟.气功:一种心身协同学[C].第八届国际医学气功研讨会论文集.2001. 51-54.

[19]张一方,欧阳志勤.生物协同学,Lorenz模型和种群动力学[J].生物数学学报.2003,18(2): 218-223.

[20]Chang Yi-Fang. Environment, population dynamics and ecological synergetics[J]. International Journal of Environment and Bioenergy.2013,7(1): 18-27.

[21]陈兰荪.数学生态学模型与研究方法[M].北京:科学出版社.1991.

[22]马知恩.种群生态学的数学模型与研究[M].合肥:安徽教育出版社.1996,96-106.

[23]Chang Yi-Fang. Social synergetics, equations on the rule of law and two-party mechanism[J]. International Journal of Modern Social Sciences. 2013,2(1):10-19.

[24]Chang Yi-Fang. Potential exploration of cold fusion and its quantitative theory of physical-chemical-nuclear multistage chain reaction mechanism[J]. International Journal of Modern Chemistry. 2013,5(1):29-43.

[25]张一方.知识经济和人-自然协同学[C].中国知识经济文选.中国经济出版社.2000.1. 275-278.

[26]I.普里戈金,曾庆宏,沈小峰译.从存在到演化[M].上海:上海科学技术出版社.1986.

[27]I.普里戈金.I.斯唐热,曾庆宏,沈小峰译.从混沌到有序[M].上海:上海译文出版社.1987.

[28]尼科里斯,普里戈金,罗久里,陈奎宁译.探索复杂性[M].成都:四川教育出版社.1986.

[29]普里戈金,湛敏译.确定性的终结[M].上海:上海科技教育出版社.1998.

[30]张一平,张一方.开放系统负熵流输入的适度性[C].熵,信息与交叉科学.喻传赞等编.云南大学出版社.1994.79-84.

[31]张一方.孤立系统的内部机制和热力学第二定律局限性的新探索[C].熵、信息与交叉科学.喻传赞等编.昆明:云南大学出版社.1994. 53-60.

[32]Chang Yi-Fang. Possible decrease of entropy due to internal interactions in isolated systems[J]. Apeiron. 1997, 4(4):97-99.

[33]Chang Yi-Fang. Entropy, fluctuation magnified and internal interactions[J]. Entropy. 2005, 7(3): 190-198.

[34]Chang Yi-Fang. Entropy decrease in isolated system and its quantitative calculations in thermodynamics of microstructure[J]. International Journal of Modern Theoretical Physics. 2015,4(1):1-15.

[35]Chang Yi-Fang. “Negative temperature” fallacy, sufficient-necessary condition on entropy decrease in isolated systems and some possible tests in physics, chemistry and biology[J]. International Review of Physics. 2012,6(6):469-476.

[36]Chang Yi-Fang. Possible entropy decrease in biology and some new research of biothermodynamics[J]. NeuroQuantology. 2013,11(2):189-196.

[37]Chang Yi-Fang. Social thermodynamics, social hydrodynamics and some mathematical applications in social sciences[J]. International Journal of Modern Social Sciences. 2013,2(2): 94-108.

[38]Chang Yi-Fang. Entropy decrease in isolated system and its quantitative calculations in thermodynamics of microstructure[J]. International Journal of Modern Theoretical Physics. 2015,4(1):1-15.

[39]张一方,郭国霖.孤立系统中的自组织与熵增疑难[C].21世纪100个交叉科学难题.李喜先主编.北京:科学出版社.2005.1.214-218.

[40]Y.Shokef, G.Shulkind and D.Levine. Isolated nonequilibrium systems in contact[J]. Phys.Rev. 2007, E76(3):030101(R).

[41]N.Erez, G.Gordon, M.Nest and G.Kurizki. Thermodynamic control by frequent quantum measurements[J]. Nature. 2008, 452,724-727.

[42]M.艾根,P.舒斯特尔,曾国屏,沈小峰译.超循环论[M].上海:上海译文出版社.1990.

[43]Chang Yi-Fang. Nonlinear whole biology and loop quantum theory applied to biology[J]. NeuroQuantology. 2012,10(2):190-197.

[44]Chang Yi-Fang. Structure-function-result mode in sociology, hypercycle and knowledge economic theory[J]. International Journal of Modern Social Sciences. 2013,2(3):155-168.

[45]P.R.A.Campos, J.F.Fontanari and P.F.Stadler. Error propagation in the hypercycle[J]. Phys.Rev. 2000,E61(3):2996-3002.

[46]C.P.Ferreira and J.F.Fontanari. Nonequilibrium phase transitions in a model for the origin of life[J]. Phys.Rev. 2002, E65(2):021902.1-10.

[47]A.Montina, U.Bortolozzo, S.Residori and F.T.Arecchi. Non-Gaussian statistics and extreme waves in a nonlinear optical cavity[J]. Phys.Rev.Lett. 2009,103(17):173901.1-4.

[48]张一方.超循环论的图论矩阵表示及其发展与应用[J].吉首大学学报.2011,32(2):36-41.

[49]张一方.多连通拓扑和东方经济学的原理及其数学分析[J].吉首大学学报.2010,31(4): 59-66.

[50]张一方.老庄哲学与可持续发展的经济观[J].商丘师范学院学报. 2010,26(5):16-18.

[51]Chang Yi-Fang. Multiply connected topological economics, nonlinear theory of economic growth and its three laws, and four theorems on knowledge economic theory[J]. Global Journal of Science Frontier Research. Mathematics and Decision Science. 2012,12(13)V1.0: 1-13.

[52]Chang Yi-Fang. Social thermodynamics, social hydrodynamics and some mathematical applications in social sciences[J]. International Journal of Modern Social Sciences. 2013,2(2): 94-108.

[53]张一方.东方经济学,经济拓扑学,经济进化论和循环经济[J].吉首大学学报.2011, 32(1):98-104.

[54]E.拉兹洛.微漪之塘[M].钱兆华译.社会科学文献出版社.2001.34.

[责任编辑：闫昕]

Synergetics, Theory of the Dissipative Structure and Supercycle Theory

CHANG Yi-fang

(Department of Physics, Yunnan University, Kunming 650091, China)

Abstract：First, synergetics and its applications are discussed, and it shows that life lies in cooperation in chaos. Next, theory of the dissipative structure and some questions are researched, and entropy decrease in an isolated system is investigated. Finally, we discuss the supercycle theory, which may be defined by a degree of connectivity. Moreover, their possibly developed directions are proposed.

Key words: synergetics; theory of the dissipative structure;supercycle theory; nonlinearity