如何进行数学开放题教学

邹淑衡

【摘 要】数学开放题教学应注意低起点、趣味性，重过程，重小结，重师生互动、生生互动。

【关键词】数学开放题教学；学生的学习兴趣；实践

随着开放性试题在中考和高考试题中频频出现，数学开放题越来越多地被师生所关注，也越来越快地成为数学教学中的热点问题。因此，加强对开放题及其教学的研究就显得十分必要。

实施开放题教学时，在新课的引入、课堂结构设计、例习题的处理、课内外作业等方面应注意采取不同的形式，从而使学生积极参与到教学活动中，真正体现学生的主体地位和教师的主导作用。

一、在新课引入中融入适当的开放题，激发学生的学习兴趣

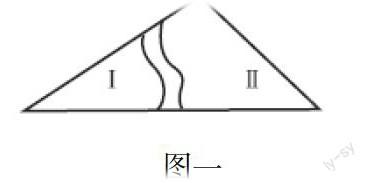
兴趣是成功的一半，教学必须以学生兴趣为起点。为此，在新课的引入上，应通过设置适当的开放性问题，使学生较快地进入新的学习情境。如对三角形全等的ASA公理的教学，可先提出这样一个问题：一块三角形形状的玻璃被打碎成两片（如图1），配一块同样大小的三角形玻璃要不要两块都带？若只带一块，则应带哪一块？为什么？学生思考上述问题时，已感知到ASA这一判定公理，并且兴趣很浓。

图一

二、在课堂结构设计中融入开放性问题，让学生参与知识形成过程

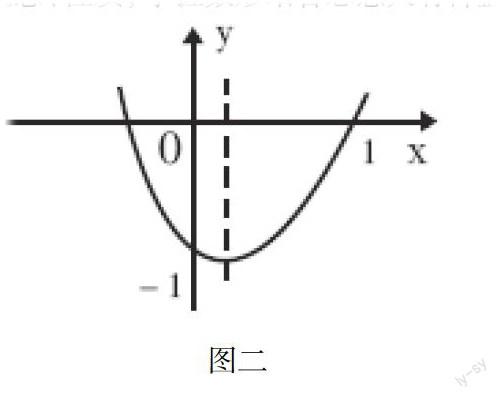
在课堂结构设计中想方设法营造轻松、活泼的课堂教学氛围，在师生之间、学生之间造成“情意共鸣、沟通信息、反馈流畅、思维活跃”的最佳情境，达到培养学生发散思维的目的。提倡在课堂上敢说、敢想、敢疑、敢动手操作、敢于探索，教师在帮助学生解疑时要善于、敢于暴露思维过程，营造一个开放的情境。如在教学“二次函数的图像”一节时，笔者设计了这样一道题：已知二次函数的图像如图2所示，由图可以得到的哪些关系和结论？通过“放开”，让学生自己去尝试、探索，这对理解概念、性质，掌握数形结合思想大有裨益。

图二

三、改造例、习题为开放性问题，为学生提供想象的空间

在例、习题的教学过程中，可以通过添加猜测过程，不给出命题的结论，抽掉命题的部分条件等方法，将课本中例、习题变“封闭”为“开放”。例如在教学例题：“求证顺次联接四边形四条边的中点，所得的四边形是平行四边形”时，我们可以把它改编为“画出一个四边形，顺次连接四边形四条边的中点，观察所得的图形是什么图形？并加以证明”，这时我们可得如下变式：变式1，连结长方形、菱形、正方形、等腰梯形各边中点，让学生画图→观察→探求规律，从而发现结论。变式2，连接任意四边形各边中点，让学生画图→猜想→转化，从而得出结论。变式1，当一般四边形的两条对角线分别满足什么条件时，顺次连接各边中点所得四边形为菱形？矩形？正方形？会是梯形吗？引导学生展开想象，使学生余兴无穷。

在教学中老师需要注意以下几点：

（1）开放题的教学内容应满足起点低，切合学生的实际或来源于学生的生活，是通过学生现有的知识能够解决的问题，有趣味性，是学生愿意研究的。

（2）注重过程。开放题有多种解题策略，不同的答案，学生能否找到全部的解法，是否找到了最佳的答案，寻找结果不是关键。老师的首要任务应该是注重开放性教学的过程，让学生的思维活跃起来，提高学生综合分析问题、解决问题的能力，使学生养成一种创新意识，一种独立思考的习惯。

（3）重视师生互动、生生互动。在教学前，老师应该首先对学生的思维过程作大致的估计，对课堂结构做总体构思。课堂上提倡先个人探索，老师做适当的引导，然后小组讨论，进行学生间的交流，最后由老师组织全班交流。

（4）重视小结。开放题有利于学生思维的发散创新，因此，老师要做好小结。当一道开放题的各种策略都运用了，各种结论都推断出来时，老师应带领学生一起小结，比较各种策略间的优缺点，找找结论间的层次性和规律性，这是教学过程中不可或缺的环节。

参考文献：

[1]宋训邦.开放题在数学教学中的作用[J].中学教学参考，1997（6）.

[2]胡仁德.数学开放性试题三例[J].数学通讯，2002（1）.

[3]俞求是.中学数学教科书中的开放题[J].中学数学教学参考，1999（4）.

[4]张奠宙.题型开放与思想开放[J].数学教学，1994（3）.

[5]刘士勇，李宏军.数学开放题型浅析[J].中学教与学，2000（7）.

[6]曾昭成.数学开放题类型分析[J].中小学教材教学，2004（27）.

[7]张彦.数学开放题及其编制方法[J].数学教学，1999（6）.

[8]张琼.试析中考试题中的数学开放题[J].黔南民族师范学院学报，2001（3）.

[9]王琛.例谈传统题形成开放题的五条途径[J].数学教学研究，2002（6）.