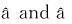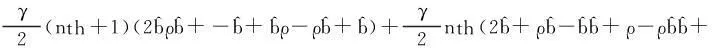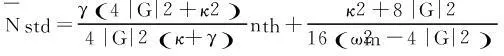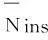结构相对数在结构分析运用中的费解
2016-01-08游新彩
结构相对数在结构分析运用中的费解*

游新彩
(吉首大学商学院,湖南 吉首 416000)
摘要:结构相对数是综合指标中最重要的指标之一,运用十分广泛.其理论内涵和算法似乎很完善,但在结构分析运用中常出现令人费解的情形,说明结构相对数还存在缺陷.通过推敲内涵,列示典型实例,显摆问题,分析产生问题的原因.指出必须区分总体基本结构和派生结构,在算法方面进一步细化,对派生结构的计算作例外规定,才能适应各种统计分析的需要.
关键词:结构相对数;推敲;完善;费解
文章编号:1007-2985(2015)01-0019-02
中图分类号:O213 文献标志码:A
DOI:10.3969/j.issn.1007-2985.2015.01.006
收稿日期:*2014-03-11
作者简介:游新彩(1963-),男,湖南益阳人,吉首大学商学院教授,主要从事统计学理论研究.
DOI:10.3969/j.issn.1007-2985.2015.01.007

总体特征常会从其结构上体现出来,结构分析就成为各种统计分析的主要内容.结构相对数作为反映总体结构唯一的综合指标,运用十分普遍,似乎在理论和实际应用都很成熟,但在某些方面还有进一步推敲的必要.
1费解实例
财务分析中结构分析是重中之重,诸如收入结构、成本结构、利润结构和现金流结构等,都是财务分析必须要深入研究的.文中以“三一重工”股份有限公司为例进行讨论.表1系根据“三一重工”股份有限公司2011年年报综合统计而得.

表1 三一重工2011年现金净流量和利润结构
不难发现,表1中存在以下2个问题:
(1)总体中的一部分,筹资活动的现金净流量比例已超过100%,主营业务利润、投资收益、营业外收支净额等3项比例之和也超过100%,这与结构相对数的概念相矛盾.
(2)总体结构是可以用平面或立体图来形象地描述其状况的,Excel和Spss等软件都有总体结构绘图功能.表1中2种结构却无法用图形来描述,违背常态.
这种现象在公司财务结构中并不少见,既不能说明指标数值的具体经济含义,也无法用结构相对数的原理解释其合理性.
2查根索源
之所以出现上述令人费解的问题,是因为结构相对数的概念不够完善而导致的.究其原因,主要体现在以下2个方面:
(1)总体基本结构与派生结构的差异.计算结构相对数的基础是统计分组,而统计分组是将总体单位按分组标志在各组间进行分配,形成次数分布数列.计算结构相对数的第1层次是依据次数分布数列的总体单位分布状况,也就是用总体单位总数这一总量指标来计算,称为总体基本结构.总体单位是客观存在的事物,它的数量不可能出现负数,当然不可能出现上述令人费解的问题.次数分布数列的进一步延伸就是计算各组和全总体的总体标志总量指标,延伸计算的总体标志总量也能反映总体结构,称之为总体派生结构,当然有可能与总体单位总数反映的总体结构不一致.如果某些总体单位的标志是负值,就可能出现上述令人费解的问题.
(2)统计指标与会计指标的差异.统计中的总量指标数值不允许有相反方向的值同时存在,一般是正数.会计中某些财务指标允许有相反方向的值同时存在,可正可负.比如企业的“利润”指标,统计上企业收大于支实现的赢利统计为“利润”,企业收不抵支统计为“亏损”,“亏损”在统计上是不能称之为“利润”的.会计报表中“利润”这一财务指标是可正可负的,实现的赢利在报表中用正数列示,出现亏损则用负数列示,正或负值都列在“利润”这一指标下,这是会计方法所允许的.正因为2专业在指标处理上存在差异,所以使得财务结构分析在运用结构相对数时出现上述令人费解的问题.
3解题释疑
要解决前面所述问题,应从以下2方面考虑:
(1)细化结构相对数的算法.设总体有N个总体单位,其总体标志总量为M,统计分组后可分组成N1,N2,N3,…,Nk个部分,各部分对应的标志总量分别为M1,M2,M3,…,Mk,显然,N1+N2+N3+…+Nk=N,M1+M2+M3+…+Mk=M,则总体结构相对数的算法见表3.表3反映了总体结构有2个层次,一是由总体单位总数计算的基本结构,二是由总体标志总量计算的派生结构.

表3 结构相对数的算法
(2)总体派生结构的例外规定.极少数经济指标是一种合成指标.如“进出口净额”,有“顺差”和“逆差”2种情况,“顺差”以正数列示,“逆差”以负数列示;又如“财政收支净额”,财政“节余” 以正数列示,财政“赤字”以负数列示.财务指标中的“利润”、“现金净流量”、“投资收益”等最为典型,都是有正有负的.这类指标在运用结构相对数作结构分析时就有可能出现令人费解的情形,有必要作例外规定.
(a)总体各部分标志总量M1,M2,M3,…,Mk中出现了负值,其中某个部分标志总量Mi>M或︱-Mi︱>M,则不能计算结构相对数.表1中现金净流量的后2项就是这种情况,此时不能计算结构相对数.
(b)总体各部分标志总量M1,M2,M3,…,Mk中出现了负值,其中任意Mi 总之,费解的情形已经提出,也是统计学理论必须解决的问题. 参考文献: [1]栗方忠.统计学原理.沈阳:东北财经大学出版社,2004. [2]黄良文,陈仁恩.统计学原理.北京:中央广播电视大学出版社,1996. [3]陈少华.财务报表分析方法.厦门:厦门大学出版社,2011. [4]张新民.财务报表分析.北京:中国人民大学出版社,2011. [5]郭富初.财务分析学.北京:首都经济贸易大学出版社,2008. [6]李鸥.揭示奥秘之数—结构相对数.中国统计,2001(7):51-53. [7]王涛.结构分析的统计方法与应用.统计与咨询,2011(5):26-27. Inexplicability of Structural Relative Number in Structure Analysis Application YOU Xincai (College of Business,Jishou University,Jishou 416000,Hunan China) Abstract:Structural relative number is one of the most important indexes in the comprehensive indexes,and is widely used.The connotation of the theory and the algorithm seems to be perfect,but in the structural analysis,some puzzling situations often appear in operation,which suggests the presence of defects in the structural relative number.In this paper,through elaborating connotation,listing the typical examples,presenting the problems,and analysing the cause of the problem,it is pointed out that the general basic structure and derivative structure must be distinguished,further refinement must be made in the aspect of algorithm,exceptions must be provided for calculating the derived structure,so that the needs of various statistical analysis can be met. Key words:structural relative number;refining;improvement;inexplicability (责任编辑陈炳权) Article ID:1007-2985(2015)01-0021-07 Dynamical Dissipative Cooling of a Cavity Opto-Mechanical Oscillator* MI Xianwu,LI Xiuhong Abstract:The dynamical cooling process of a cavity opto-mechanical system is investigated by a master equation.The mean phonon number is calculated using the covariance approach.Firstly,the effect of different cavity dissipation rate on the mean phonon number is discussed in the strong coupling system.Then the variation of mean phonon number changing with different parameters in the weak and strong coupling system is compared.For strong coupling regime,the mean phonon number oscillates periodically with the increase of coupling strength and it decreases fast as the cavity dissipation rate increases.Finally,it reaches a cooling limit.In the weak coupling regime,the mean phonon number increases fast as the cavity dissipation rate increases and it reaches equilibrium in the end. Key words:dynamical dissipative cooling,mean phonon number,strong coupling system CLC number:O47Document code:A *Received date:2014-08-12 Foundation item: Project supported by the National Science Foundation of China (10647132);Scientific Research Fundation of Hunan Provincial Education Department,China (10A100) Biography:MI Xianwu(1973—),male,was born in Hunan,China;received the microelectronics and solic state electronics Ph. D degree from the graduate school of Chinese Academy of Sciences;research interests include theoretical aspects of semiconductor lasers and amplifiers and terahertz physics. 1Introduction As we all know,optical micro-cavity,nano-mechanical and electrical systems have been widely used,but recently there is other two independent systems coupled together through interaction between radiation light pressures.Actually,in the past 50 years the radiation light pressure and the relevant physics research have long been recognized as an important subject in the atomic physics,and the resulting cavity mechanical system is closely related to them.The problem of cooling the mechanical oscillator has been a research hotspot in recent years.Now the most concerned problem is how to cool the oscillator to the ground state of energy.Because we want to see many fancy quantum phenomena after cooling the oscillator to the ground state,such as the Schrödinger cat state,quantum entangled state,etc.For different vibration frequency of the oscillator,the corresponding ground state temperature is different.For 109Hz oscillator,the temperature is 50 mk.With the loss of the vibration frequency,the critical temperature also decreases.So for general NEMS system,it is useless to make it to the ground state by lowering the environment temperature.The only way is cooling it actively.In recent years,the progress of this experiment is large,but not a landmark experiment shows that the oscillator can be cooled to the ground state.However,in 2011 a team comes from California institute of technology and the University of Vienna,cooling the nanomechanical resonator to the ground state by a bunch of laser,namely the lowest energy state.This result paved the way for the research of highly sensitive sensors and quantum experiments.The relevant research report was published on the journal Nature . In fact.For example,the coupling between optical and mechanical system has been observed by many research teams,for example,Walther observed radiation light pressure in their pioneering work and confirmed the existence of the bistable effect,of course,in the field of microwave,which was observed by Braginsky much earlier.In addition to that,the correction of mechanical oscillator stiffness coefficient caused by radiation light pressure (optical spring) has also been observed in the experiments[2-9].In this article,we will control the cooling and heating process of the system by changing the magnitude of the dissipation rate,at the same time,in different coupling system,we compare the influence of the dissipation rate and coupling strength to the whole system. Fig.1 Diagram of a Cavity Optomechanical System In order to understand how optical degree of freedom and mechanical degree of freedom coupling together,we consider a kind of typical cavity optical mechanical system,a standard Fabry-Perot resonant cavity,as illustrated in fig.1,in which a mirror at one side can vibrate freely,and the other side is fixed.When the cavity is driven by a bunch of laser,the cycle vibration light field in the optical cavity will generate a radiation pressure to the movable mirror.The force makes the mirror produce forced vibration;in turn,the tiny changes of the mirror’s position will change the effective length of optical cavity,and thus it changes the light intensity distribution in the cavity because the vibration mode of the optical cavity has changed.It is this dynamic coupling that leads to a series of interesting phenomenon. Thus,the linearized system Hamiltonianis[10] (1) Considering the dissipation effect,the quantum master equation is (2) (3) Now,taking the counter-rotating terms into consideration,we obtain the following differential equations (4) (5) Here the first term is the classical cooling limit.The second term is the quantum cooling limit.In the strong coupling system,eq. (5) reduces as (6) However,in the weak coupling system,the final phonon occupancy can be writen as (7) (8) whereΓ=4|G|2/κ is the cooling rate. In the strong coupling system,neglecting the counter-rotating term and directly solving the eq.(3),the mean phonon number is (9) where (10) are the eigen-frequencies of the normalmode.Next,taking the counter-rotating terms into consideration,solving the equations (4) and settingnth=0,we obtain (11) Hence in the strong coupling system,the time evolution of the mean phonon number is (for details see supplementary material [16]) (12) Here the first term comes from energy exchange between optical and mechanical modes;the second term is induced by quantum backaction. (13) (14) So the instantaneous-state cooling limit is (see supplementary material [16]) (15) 2The Numerical Results and Discussion In fact,we can realize the dynamic control of cavity dissipation experimentally by using a light absorber/scatter[17]or modulating free-carrier plasma density[18-20].In order to observe quantum effects experimentally,we have to overcome the thermal noise which is one of the ultimate goals in quantum physics.Cavity opto-mechanics is a remarkable example[21-22];however,the most important thing is to get the mechanical resonator into the quantum regime[23-25].In this paper,we take a generic opto-mechanical system as an example,discussing the cooling problem of the system and the variation of mean phonon number with the change of different parameters in the weak and strong coupling system. The parameter values used for the numerical simulation are:dissipation rate of the mechanical mode isγ/ωm=10-5,and thermal phonon number at the environmental temperatureTisnth=103.Fig. 2 displays Fig.2 Time Evolution of Mean Phonon Number N b with Different Cavity Dissipation Rate κ(t). the time evolution of mean phonon numberNbwith different cavity dissipation rateκ/ωm=0.01,1 in the strong coupling system,the linear coupling strength |G|/ωm=0.1.In fig. 2,we plot the numerical results based on the master equation for variousκ.It shows that whenκ/ωm=0.01,the envelope of the mean phonon number decreases gradually with the increase of time;at last it reaches and remains near the steady-state cooling limit(the dash-dotted line),given by eq.(5),but it cannot reach the instantaneous-state cooling limit (the dotted line),given by eq.(15).However,whenκ/ωm=1,the oscillation frequency becomes larger and the envelope of the mean phonon number keeps at a stable level.Most importantly it always below the steady-state cooling limit (the dashed line),given by eq.(5) and the instantaneous-state cooling limit (the dotted line).That is to say,by increasing the cavity dissipation rate,we can accelerate the cooling process. Fig.3 Three Dimensional Diagram About the Mean Phonon Number in the Strong Coupling System In fig.3 we plot the three dimensional figure about the mean phonon number in the strong coupling system forγ/ωm=10-5,nth=103andωmt=30.It shows that in the strong coupling regime,the mean phonon number decreases gradually before the cavity dissipation rateκ/ωm≈1;afterκ/ωm≈1 the mean phonon number decreases quickly;at last it reaches and remains a stable limit.As the increase of the coupling strengthG/ωm,the mean phonon number oscillates periodically,and whenG/ωm=0.02~0.05,there occurs a small crest which consist of many sine waves.After that there occurs a larger crest and cycles periodically as the same crest value. In Fig 4,we plot the three dimensional figure about the mean phonon number in the weak coupling Fig.4 Three Dimensional Figure About the Mean Phonon Number in the Weak Coupling System system forγ/ωm=10-5,nth=103andωmt=200.On the contrary,in the weak coupling regime,the mean phonon number increases gradually as the increase of the cavity dissipation rateκ(t)/ωm.At last it reaches and remains a limit.What’s more,as the increase of the coupling strengthG/ωm,the mean phonon number doesn’t show periodically oscillation.That is to say,in the weak coupling regime,increasing the cavity dissipation rate is able to accelerate the heating process.At the same time,it may also strongly cause the heating noise. 3Conclusion In summary,we discussed the dynamic cooling problem of an opto-mechanic coupling system,compared the influence of different dissipation rate of the optical cavity mode on the mean phonon number in the strong coupling system.In a certain range,the larger of the cavity dissipation rate,the smaller of the mean phonon number,and with the larger cavity dissipation rate,the mean phonon number can reach the instantaneous-state cooling limit quickly.That is to say,by increasing the cavity dissipation rate,we can accelerate the cooling process.For strong coupling regime,with the increase of the coupling strength,the mean phonon number oscillates periodically;at the same time,the mean phonon number decreases fast as the cavity dissipation rate increases.In the end,it reaches a cooling limit.On the contrary,for weak coupling regime,the mean phonon number increases fast as the cavity dissipation rate increases,and then it reaches equilibrium.What’s more,with the increase of the coupling strength,the mean phonon number doesn’t occur periodically oscillation.So in the weak coupling system,increasing the cavity dissipation rate is able to accelerate the heating process. References: [1]CHAN J,MAYER ALEGRE T P,AMIR H,et al.Laser Cooling of a Nano Mechanical Oscillator into Its Quantum Ground State.Nature,2011,478:89-92. [2]SHEARD B S,GRAY M B,MOW-LOWRY C M,et al.Observation and Characterization of an Optical Spring.Phys.Rev.A,2004,69(5):051 801. [3]BRAGINSKY V B,STRIGIN S E,VYATCHANIN S P.Parametric Oscillatory Instability in Fabry-Perot Interferometer.Physics Letters A,2001,287(5/6):331-338. [4]KIPPENBERG T J,ROKHSARI H,CARMON T,et al.Analysis of Radiation-Pressure Induced Mechanical Oscillation of an Optical Microcavity.Phys.Rev.Lett.,2005,95:003 901. [5]ARCIZET O,COHADON P F,BRIANT T,et al.Radiation-Pressure Cooling and Optomechanical Instability of a Micromirror.Nature,2006,444(7 115):71-74. [6]SCHLIESSER A,DEL’HAYE P,NOOSHI N,et al.Radiation Pressure Cooling of a Micromechanical Oscillator Using Dynamical Backaction,.Phys.Rev.Lett.,2006,97(24):243,905. [7]THOMPSON J D,ZWICKL B M,YARICH A M,et al.Strong Dispersive Coupling of a High Finesse Cavity to a Micromechanical Membrane,.ArXiv:0707.1724 (2007). [8]POGGIO M,DEGEN C L,MAMIN H J,et al.Feedback Cooling of a Cantilever’S Fundamental Mode Below 5 mK.Phys.Rev.Lett.,2007,99(1):017 201. [9]MARSHALL W,SIMON C,PENROSE R,et al.Towards Quantum Superpositions of a Mirror.Phys.Rev.Lett.,2003,91(13):130 401. [10] LIU Y C,XIAO Y F,LUAN X S,et al.Dynamical Dissipation Cooling of a Mechanical Oscillator in Strong-Coupling Optomechanics.ArXiv:1303.3657 (2013). [11] MARQUARDE F,CHEN J P,CLERK A A,et al.Quantum Theory of Cavity-Assisted Sideband Cooling of Mechanical Motion.Phys.Rev.Lett.,2007,99:093 902. [12] DOBRINDT J M,WILSON-RAE I,KIPPENBERG T J.Parametric Normal-Mode Splitting in Cavity Optomechanics.Phys.Rev.Lett.,2008,101:263 602. [13] WILSON-RAE I,NOOSHI N,DOBRINDT J,et al.Cavity-Assisted Back Action Cooling of Mechanical Resonators.New J.Phys.,2008,10:095 007. [14] WILSON-RAE I,NOOSHI N,ZWERGER W,et al.Theory of Ground State Cooling of a Mechanical Oscillator Using Dynamical Backaction.Phys.Rev.Lett.,2007,99:093 901. [15] MARQUARDT F,CHEN J P,CLERK A A,et al.Quantum Theory of Cavity-Assisted Sideband Cooling of Mechanical Motion.Phys.Rev.Lett.,2007,99:093 902. [16] LIU Y C,XIAO Y F,LUAN X S,et al.Supplementary Material for:Dynamical Dissipation Cooling of a Mechanical Oscillator In Strong-Coupling Optomechanics.ArXiv:1303.3657 (2013). [17] FAVERO I AND KARRAI K.Cavity Cooling of a Nanomechanical Resonator by Light Scattering.New J.Phys.,2008,10:095 006. [18] XU Q,DONG P,LIPSON M.Breaking the Delay-Bandwidth Limit in a Photonic Structure.Nature Phys.,2007,3(6):406-410. [19] KONDO K,SHINKAWA M.Ultrafast Slow-Light Tuning Beyond the Carrier Lifetime Using Photonic Crystal Waveguides.Phys.Rev.Lett.,2013,110:053 902. [20] SOREF R A,BENNETT B R.Electrooptical Effects in Silicon.IEEE J.Quantum Electron.,1987,23(1):123-129. [21] KIPPENBERG T J,VAHALA K J.Cavity Optomechanics:Back-Action at the Mesoscale.Science,2008,321:1 172-1 176. [22] MARQUARDT F,GIRVIN S M.Optomechanics.Physics,2009(2):40. [23] TEUFEL J D.Sideband Cooling of Micromechanical Motion to the Quantum Ground State.Nature (London),2011,475:359-363. [24] CHAN J,MAYER ALEGRE T P,SAFAVI-NAEINI A H,et al.Laser Cooling of a Nanomechanical Oscillator Into Its Quantum Ground State.Nature (London),2011,478:89. [25] VERHAGEN E,DELEGLISE S,WEIS S,et al.Quantum-Coherent Coupling of a Mechanical Oscillator to an Optical Cavity Mode.Nature (London),2012,482:63.