圆型图像特征点检测算法
2016-01-08黎票,杨天龙,廖建国等
圆型图像特征点检测算法*

黎票,杨天龙,廖建国,赵前程
(湖南科技大学机电工程学院,湖南 湘潭 411201)
摘要:为了提高圆型图像特征点检测算法的准确性和稳定性等,提出了一种基于圆型特征图像中心灰度对称的检测算法.先利用Sobel算子进行圆型特征图像边缘检测,然后采用灰度质心法求出圆型特征图像的中心,最后引入灰度对称因子获得圆型图像特征点的亚像素位置坐标.用仿真投影实验和实际实验来评估算法精度,结果表明新算法精度可控制在0.2个像素左右.
关键词:特征点;亚像素;角点检测;摄像机标定
文章编号:1007-2985(2015)01-0028-07
中图分类号:TP391文献标志码:A
DOI:10.3969/j.issn.1007-2985.2015.01.008
收稿日期:*2014-07-16
基金项目:国家自然科学基金资助项目(51275169,51345009);湖南省教育厅高校科研资助项目(12C0117)
作者简介:黎票(1987—),男,湖南长沙人,湖南科技大学机电工程学院硕士生,主要从事机械设计、图像处理和机器视觉研究;赵前程(1969—),男,安徽合肥人,湖南科技大学机电工程学院教授,博士,主要从事精密计量测试技术、在线检测、图像处理和机器视觉等研究.

在三维视觉检测中,圆和椭圆特征点是需要经常处理的图像特征[1-3].实际应用中,常见的圆和椭圆特征有被测零件上的定位孔和标定靶上的特征图像等.尤其在实现摄像机或传感参数的标定时,也经常是基于立体球靶或平面圆靶为图像特征对象的.圆型靶标因其形状特征独特的优势,且圆型靶标的特征点容易识别提取,故圆型靶标在摄像机标定等领域应用比较多.而圆型图像特征点检测的精度直接影响摄像机标定的精度.
常用的圆型图像特征点检测算法比较多[4-7],大部分是基于Hough变换的检测算法、基于最小二乘拟合的检测算法以及基于椭圆的几何特征检测算法.对于相对较小,只有几个或者十几个像素大小的椭圆及圆孔图像,通常用重心法进行处理就非常有效.重心法包括带有阈值的重心法和平方加权重心法.夏瑞雪等利用自适应阈值分割和最小二乘椭圆拟合实现圆点靶标图像特征定位.徐鹏等根据透视不变性原理,利用圆形靶标的椭圆像的公切线求出椭圆的虚圆心像点坐标.安新源等[10]通过最小二乘优化椭圆的参数来实现椭圆的检测.李占利等[11]根据透射投影模型误差和建立2个空间椭圆的位置关系来实现椭圆的中心的检测.该算法先利用空间矩算子实现图像边缘像素点的亚像素定位,再以光心为顶点和检测出理想的图像的边缘为准线建立2个具有投影关系的空间圆,然后根据目标的匹配关系来求出空间圆圆心的像点位置.王静等[12]提出了一种基于非极大值抑制的圆特征亚像素中心提取算法.该算法首先利用Sobel算子对图像进行边缘检测得到椭圆的边缘特征信息,并利用非极大值抑制方法对椭圆的边缘像素进行细化得到像素级边缘点坐标,然后用Zernike正交矩实现边缘点的亚像素级定位,最后利用最小二乘法进行拟合来获取图像圆特征中心的亚像素坐标.上述文献中的方法各有优点,不过存在稳定性和检测效率等方面的不足,受噪声影响比较大.
基于Hough变换椭圆检测是一种计算相对复杂的椭圆检测算法,难以实现.而基于最小二乘椭圆检测算法是最简单、最容易实现的,可是受噪声影响大,稳定性和精度不高.鉴于椭圆的几何对称特性,椭圆经过透射投影在摄像机成像的图像具有几何对称性质,为此笔者提出一种基于椭圆中心灰度对称检测算法.采用Sobel算子和灰度质心法能够快速得到椭圆图像的中心位置坐标,可有效降低噪声和其他不确定因素对角点亚像素定位精度的影响.通过仿真投影和实际试验对算法精度进行评价,将新算法与目前通用性的最小二乘拟合方法的提取结果进行比较,结果表明,新算法精度可靠,效率提升明显.
1基于椭圆中心灰度对称的检测算法
基于椭圆中心灰度对称的检测算法的基本原理为:利用Sobel算子进行边缘检测,并用灰度质心法可以快速得到椭圆的中心坐标.鉴于椭圆的几何对称性,文中引用灰度对称因子.在椭圆中心点附近取一定大小的兴趣区域,对图像椭圆的灰度进行变换,求出该区域内每个像素的权值,利用加权法实现椭圆的中心点的亚像素定位.
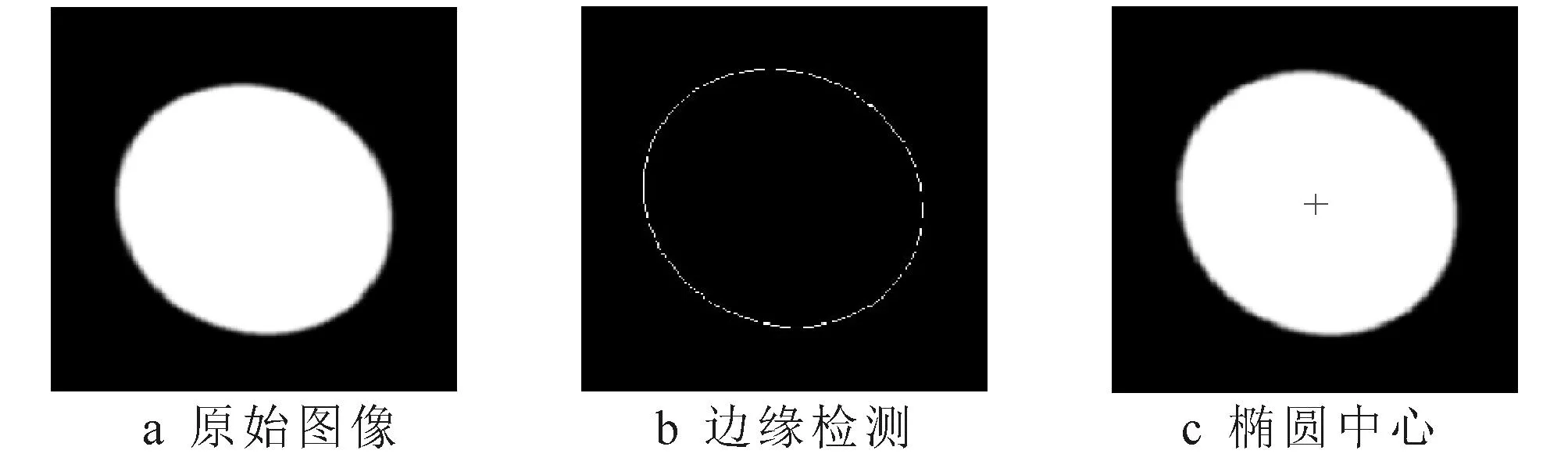
图1 椭圆检测的效果图
如图1a所示,对于一幅含有椭圆特征的图像,利用Sobel算子进行边缘检测可得其边缘轮廓图像如图1b所示,根据边缘像素点集坐标,采用质心法可获得椭圆中心的粗定位结果如图1c所示.
令I(u,v)为图像坐标系(o-uv)对应的灰度函数,以上文获得的椭圆中心为区域中心,在其附近取一个大小为W的兴趣区域,该区域需包含完整的椭圆特征信息.利用椭圆的几何对称性质,引入灰度对称因子来求取趣区域W内每个像素的权值,定义W内某像素点(u,v)所对应的灰度对称因子为
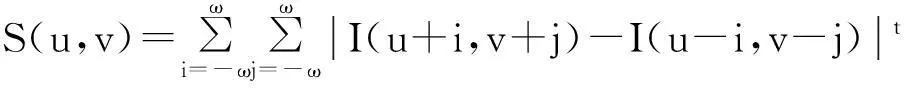

图2 灰度对称因子变化趋势图
其中ω为以像素点(u,v)为中心的方形窗口半径,t为指数.根据椭圆的几何对称性可知,若S(u,v)的值越小,说明以图像中像素点(u,v)为中心的方形窗内的椭圆的灰度中心对称性越高,对应的(u,v)越接近椭圆中心.在计算S(u,v)时,ω的取值应综合考虑镜头畸变和噪声抑制,在取ω=4,t=1时,某椭圆中心对应的兴趣区域W内的灰度对称因子S(u,v)关于坐标(u,v)的变化趋势如图2所示.
利用已求出的椭圆中心像素点邻域内的灰度对称因子S(u,v),可求出兴趣区域W内每个像素所对应的权因子C(u,v):
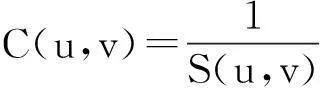
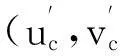
(1)

2仿真实验
本实验通过相机线性投影模型创建棋盘格图像进行仿真实验.相机线性透射投影模型如下:
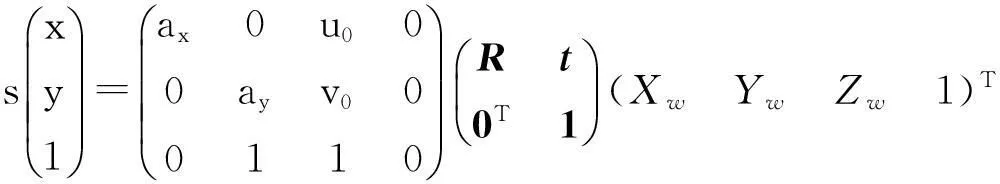
其中:(u0,v0)为主点坐标;(Xw,Yw,Zw)为世界坐标系中空间点的坐标;s为比例因子;ax,ay分别为图像坐标系u轴和v轴上的归一化焦距;R,t分别为旋转矩阵和平移矩阵.

图3 圆型仿真图像
仿真实验1利用摄像机线性投影模型创建圆和椭圆图像进行仿真实验.该仿真实验可以参考格型图像的仿真实验设置参数.其中,空间圆的半径为30 mm,空间圆心的世界坐标为(-5,-8,0);摄像机分辨率设为640×480,ax,ay设为3 200,并令u0=320,v0=240,角点世界坐标系坐标为[0,0,0,1],设R中的θx,θy,θz为0 π,t中的tx,ty在[-50 mm,50 mm]范围内随机变化,tz在[1 000 mm,2 000 mm]范围内随机变化.为使仿真图像与实际拍摄的图像相接近,对于任意一副仿真图像s0,引入标准差为σ1的高斯噪声得到图像s1,并与标准差为σ2的高斯卷积核进行卷积[13]得到边缘扩散后的仿真图像s2,如图3所示.
对于σ1,σ2不同的取值情况,每种情况运行200次仿真投影程序获得200幅仿真图像,为方便对比,在Matlab语言环境下对其分别采用新算法和最小二乘角点检测算法进行角点提取,所获得的提取结果误差统计如图4—9所示.在采用新算法进行提取时,先利用Sobel算子进行圆型图像的边缘检测,再利用质心法定位椭圆中心的位置坐标,亚像素定位时取ω=4,w=74×74,t=1.
由图4—9可知,新算法相比最小二乘法在不同噪声级别和边缘扩散程度下都具有更高的鲁棒性.
仿真实验2利用摄像机线性透射投影模型,设置仿真实验参数.其中,空间圆的半径为30 mm,空间圆心的世界坐标为(-5,-8,0);摄像机分辨率设为640×480,ax,ay设为3 200,并令u0=320,v0=240,角点世界坐标系坐标为[0,0,0,1],设R中的θy,θz为分别为-π/6,π/18,θx在[-]π/12,π/12] 范围内随机变化,t中的tx,ty,tz分别为20,10,1 500 mm.可以保持椭圆靶标真实投影的中心点不变.
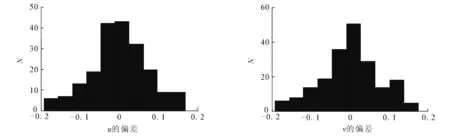
图4 偏差直方图(σ 1=0,σ 2=0,新算法提取)
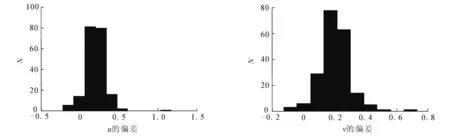
图5 偏差直方图(σ 1=0,σ 2=0,最小二乘检测算法提取)

图6偏差直方图(σ 1=10,σ 2=1,新算法提取)
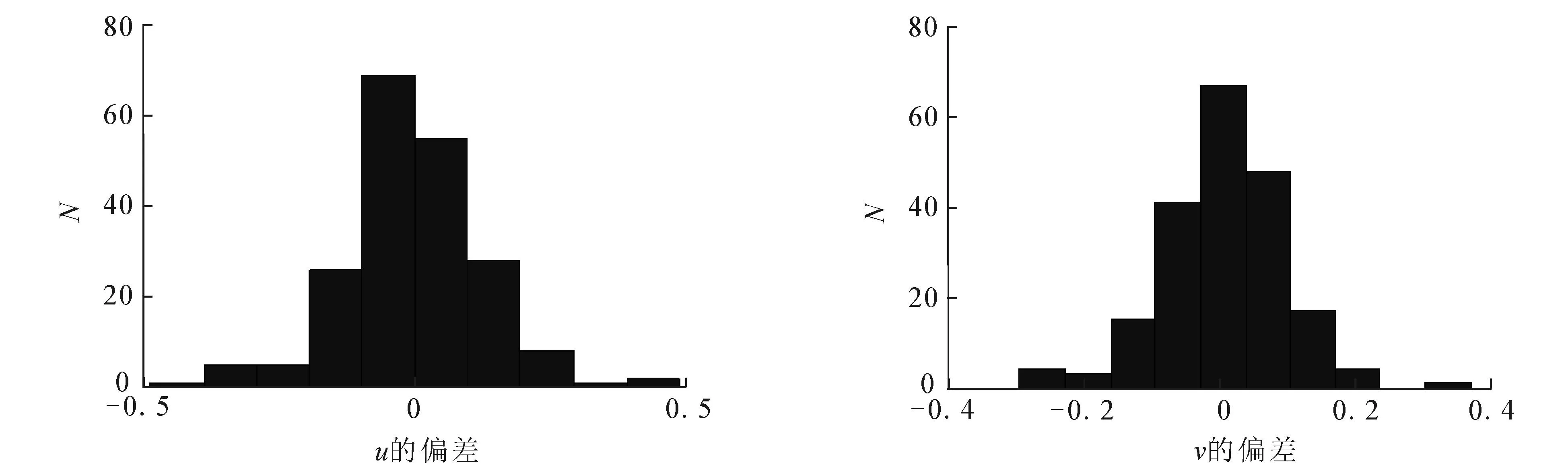
图7偏差直方图(σ 1=10,σ 2=1,最小二乘检测算法提取)

图8偏差直方图(σ 1=20,σ 2=2,新算法提取)
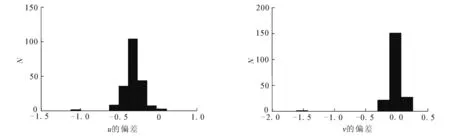
图9偏差直方图(σ 1=20,σ 2=2,最小二乘检测算法提取)

图10 椭圆仿真图像
取σ1=10,σ2=1,运行200次仿真投影程序获得200幅椭圆型仿真图像,如图10所示.由于椭圆透视投影存在畸变误差,因此利用新算法求出每幅椭圆图像特征点,并与真实投影点相减,得到每幅椭圆图像之间的投影偏差d,然后求200幅图像投影偏差d之间的偏差为Δd,u方向的偏差为Δu,v方向的偏差为Δv.图11a,11b为先利用Sobel算子进行边缘检测,再利用质心法求椭圆型图像的中心,最后利用椭圆中心灰度对称检测算法获得椭圆图像特征点的实验结果.图11c,11d为先利用Sobel算子进行边缘检测,再利用最小二乘求椭圆型图像的中心,最后利用椭圆中心灰度对称检测算法获得椭圆图像特征点的实验结果.


图11 2种方法提取结果(单位:像素)
由上面的实验可知,新算法与最小二乘检测的结果相比较,检测精度要高.
仿真实验3当摄像机与靶标处于平行的关系,也就是靶标图像的正投影时,圆投影还是保持圆的特性.该实验利用透射投影模型,旋转和平移矩阵保持不变,通过改变靶标圆半径的大小,圆的半径r在[100 mm,10 mm]范围内随机变换.靶标圆的中心点为(-5,-8,0),R中的θx,θy,θz的值都为0 π,t中的tx,ty,tz分别为20,10,1 500 mm,取σ1=10,σ2=1.可以得到不同半径大小的圆型特征图像,如图12所示.
利用新算法,求出创建得到圆型图像特征点的坐标.利用文中圆型检测方法计算得到圆型图像特征点与真实靶标圆的投影之间的偏差为Δd.实验数据结果如图13所示.
由上面的实验可知,当摄像机与靶标相平行时,靶标中圆的半径改变,利用新算法进行检测也能达到很高的精度.

图12 仿真圆特征图像
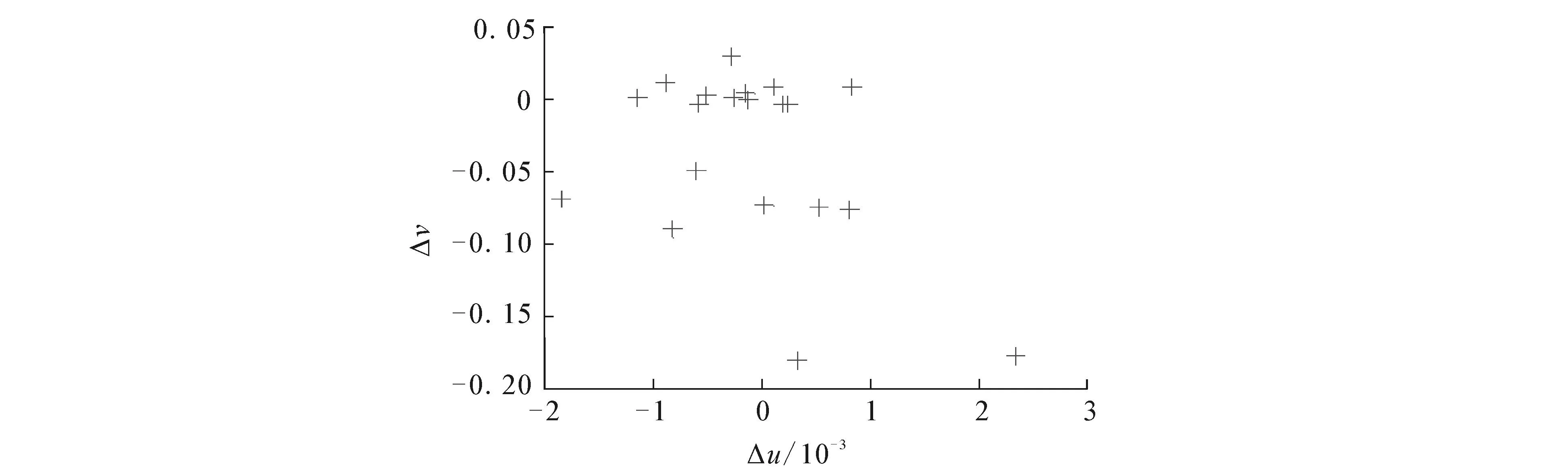
图13 误差分布
3实际实验
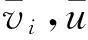
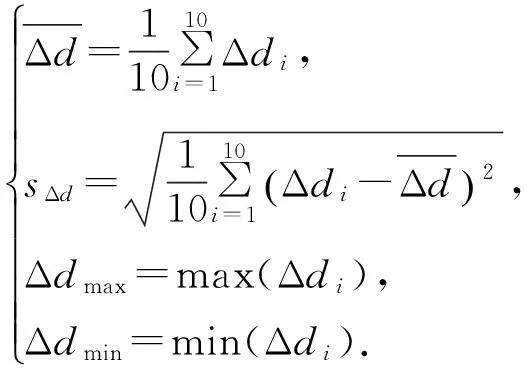

图14 圆特征图像
利用新算法和最小二乘拟合得到特征点坐标数据,并按上述公式进行计算,得到实验结果见表1,2.由表1,2可知,新算法相比最小二乘拟合法,在检测实际圆特征图像时,精度更好,稳定性更高.其中圆特征半径越小,精度越好,且受图像噪声的影响不大.
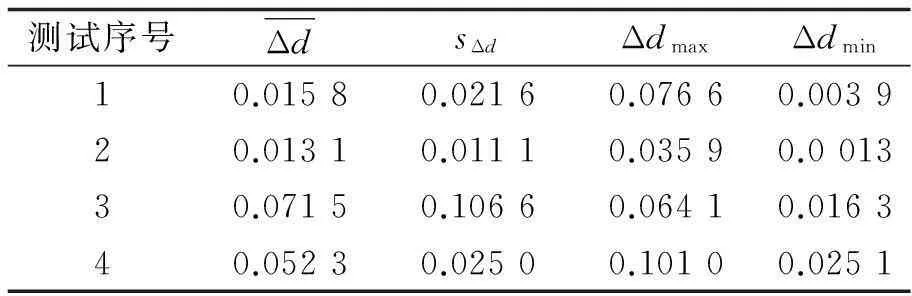
表1 新算法评价结果 像素
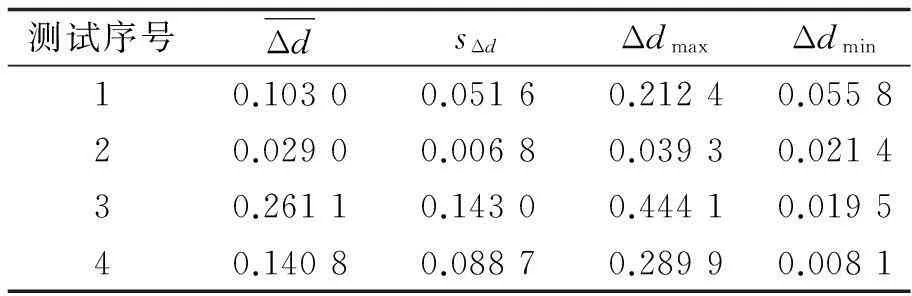
表2 最小二乘法评价结果 像素
4结语
对现阶段具有代表性的圆型图像特征点检测算法进行分析,在此基础上,针对圆特征图像的灰度分布和几何特征提出一种基于圆型特征图像中心灰度对称的检测算法.该算法采用Sobel算子进行图像边缘提取得到圆型特征图像的边缘信息,利用灰度质心法快速获取圆形特征图像像素级中心坐标,并引入灰度对称因子,采用加权法使定位精度达到亚像素级.通过仿真和实际实验进行验证,通过与最小二乘法进行比较,结果表明新算法计算速度快,效率高,受靶标位姿、环境亮度变化的影响较小,且对噪声的抑制能力较强,定位准确.
参考文献:
[1]马文娟,孟广军.采用同心圆图像的摄像机标定方法.计算机仿真,2013,30(2):410-425.
[2]陈济棠,徐杜,蒋永平,等.计算机三维视觉测量中相机标定的圆形校正方法.电子测量技术,2011,34(3):95-98.
[3]高俊鑫,华炜,章国锋,等.带约束的摄像机定标方法.中国图象图形学报,2010,15(3):536-540.
[4]吴斌,朱洪岩,肖心通,等.视觉测量中基于单应性矩阵的平面靶标图像特征提取.光电子·激光,2011,22(8):1 211-1 215.
[5]MANUELE.L,ALBERTOBR,MARCELOG.Multi-CameracalibrationBasedonanInvariantPattern.Computers&Graphics,2011(35):198-207.
[6]董明利,刘镖峰,吕乃光.基于虚拟靶标的摄像机标定.北京信息科技大学学报,2010,25(1):11-15.
[7]邹益民,汪勃.一种基于最小二乘的不完整椭圆拟合算法.仪器仪表学报,2006,27(7):808-812.
[8]夏瑞雪,卢荣胜,刘宁,等.基于圆点阵列靶标的特征点坐标自动提取方法.中国机械工程,2010,21(16):1 906-1 910.
[9]徐鹏,汪建业,王燕儒.摄像机标定中靶标圆心像点坐标的精确计算.红外与激光与工程,2011,40(7):1 342-1 346.
[10] 安新源,周宗潭,胡德文.椭圆拟合的非线性最小二乘方法.计算机工程及应用,2009,45(18):188-190.
[11] 李占利,刘梅,孙瑜.摄影测量中圆形目标中心像点计算方法研究.仪器仪表学报,2011,32(8):2 235-2 241.
[12] 王静,王海亮,向茂生.基于非极大值抑制的圆目标亚像素中心定位.仪器仪表学报,2012,33(7):1 460-1 468.
[13] 尚雅层,陈静,田军委,等.高斯拟合亚像素边缘检测算法.计算机应用机,2011,31(1):179-181.
Algorithm for Detecting Feature Points of Circle Image
LI Piao,YANG Tianlong,LIAO Jianguo,ZHAO Qiancheng
(College of Electromechanical Engineering,Hunan University of Science and Technology,Xiangtan 411201,Hunan China)
Abstract:In order to improve the accuracy and stability of circular image feature point detection,an algorithm is put forward based on the gray-scale symmetry of circular image center.Through this algorithm,the edge of circular image is firstly detected by Sobel operator;then gray-scale qualitative method is used to determine the center of the circular image;and finally gray-scale symmetry factor is introduced to obtain the sub-pixel coordinates of the feature points of circular image.Projection simulation experiment and measuring experiment are adopted to evaluate the precision of this algorithm,and the experiment results show that the precision of this method is around 0.2 pixels.
Key words:feature points;sub-pixel;corner detection;camera calibration
(责任编辑向阳洁)

