车站结构型式对地铁诱发环境振动的影响分析

第一作者赵斌男，博士，教授，1967年10月生

车站结构型式对地铁诱发环境振动的影响分析

赵斌1，杨彪1，李明文2，马忠政3

(1. 同济大学土木工程防灾国家重点实验室，上海200092；2. 上海市隧道工程轨道交通设计研究院，上海2002353.上海轨道交通十号线发展有限公司，上海201103)

摘要：地铁诱发环境振动是城市轨道交通工程设计中重点关注的课题。系统研究了地铁车站考虑地铁运行诱发环境振动的数值建模问题，给出了计算模型建立的思路及相关计算参数的取值方法。以某拟建地铁车站为例，建立了车站结构—土的准三维有限元模型，分析车站结构型式对地铁诱发环境振动的影响，从振动加速度时程反应、1/3倍频程谱和峰值衰减规律等方面对叠合墙式、复合墙式和离壁墙式三种不同型式车站方案进行了详细的对比分析。研究结果表明：分离车站结构内衬墙和地下连续墙可减小地铁诱发的环境振动。对于环境振动水平需要严格控制的地区，地铁车站可选用离壁墙式结构方案。

关键词：车站结构；离壁墙式车站；环境振动；有限元分析

基金项目：上海市建交委项目(建管2013-006-007)

收稿日期：2014-03-10修改稿收到日期：2014-09-30

中图分类号:TU921；TB533.2

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.07.019

Abstract:Considerable attention has been drawn to the environmental vibration induced by railway traffic in rail transit design. The numerical modeling strategies of metro station used for predicting the railway traffic induced environmental vibration were studied, and the practical analytic model as well as the methods of the related parameter identification were presented. Based on a proposed metro station project, a quasi-three-dimensional station dynamic structure-soil interface FEM model for the station was established to investigate the influence of station structure on the environmental vibration induced by railway traffic. Three different station structures with composite walls, compound walls and separated walls respectively were analyzed and compared in time history responses, 1/3 octave spectra and attenuation tendencies of peak acceleration. The results show that separation of lined wall and retaining wall can reduce the environmental vibration and station with separated-wall is the optimal solution for the area having high limitation of the environmental vibration.

Investigation on influences of metro station structures on environmental vibration induced by railway traffic

ZHAOBin1,YANGBiao1,LIMing-wen2,MAZhong-zheng3(1.State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092,China;2. Shanghai Tunnel Engineering & Rail Transit Design and Research Institute, Shanghai 200235,China3. ShanghaiRail Transit L10 Development Co.Ltd, Shanghai 201103,China)

Key words:metro station structure; station with separated walls; environmental vibration; finite element analysis

近年来，随着国内城市化进程的加速，地铁得到大力发展，其建造位置也距地面建筑物越来越近。地铁在运营过程中产生的振动，经岩土介质向周边地层表面和建筑物基础传播，引起周边环境和建筑物的振动，从而影响周边居民的正常工作和生活[1]，一些对振动敏感的精密仪器设备也可能受此影响而不能正常使用[2]。因此，地铁运营诱发的环境振动正成为城市轨道交通工程设计中重点关注的问题。

地铁隧道结构型式是影响地铁诱发环境振动的重要因素之一，国内外学者对此进行了相关研究。Gupta等[3]研究了隧道的埋深、尺寸及形状对地铁振动的影响。辜小安等[4]对国内一些城市地铁的环境振动进行了现场实测，对比了不同隧道结构型式和埋深下隧道壁的振动特性。田春芝[5]综合国外研究资料，总结了隧道结构型式对地铁振动的影响。目前关于车站结构型式对地铁振动影响的研究却较少。

本文对地铁车站考虑地铁运行诱发环境振动的数值建模方法进行了系统研究，以上海某拟建的地铁车站为背景，从减小地铁诱发环境振动的角度出发，采用数值模拟的方法，通过建立车站—土的准三维有限元模型，分析叠合墙式、复合墙式及离壁墙式三种车站结构方案对地铁诱发环境振动的影响，并通过对数值分析结果的对比，探讨车站结构的最佳方案，其相关方法和主要结论对同类地铁工程的车站结构选型具有很好的参考应用价值。

1工程概况

拟建的某地铁站主体结构距离某高校实验楼约50m，该实验楼中有较多对振动敏感的精密仪器，需对周围环境的振动进行严格限制，以保证其正常工作。为此，车站结构设计给出了三种备选结构方案，分别为叠合墙式、复合墙式和离壁墙式结构型式，需要通过分析研究确定最合理的技术方案。

叠合墙式车站方案在围护结构(地下连续墙)和车站内衬墙之间设置钢筋接驳器连接，叠合后两者可视为整体，如图1所示。复合墙式方案围护结构和内衬墙之间是分离的，中间设防水层，两者不能视为整体，如图2所示。离壁墙式方案围护结构和内衬墙分离一定距离，两者由横向支撑连接，如图3所示。复合墙式和离壁墙式车站都设压梁和抗拔桩用以抵抗车站上浮。三种车站方案均为钢筋混凝土结构，混凝土强度等级为C30。

图1　叠合墙式车站结构 Fig.1 Station structure with composite walls

图2　复合墙式车站结构 Fig.2 Station structure with compound walls

图3　离壁墙式车站结构 Fig.3 Station structure with separated walls

2数值建模方法

2.1计算模型

对地铁车站建立有限元模型进行计算分析时，为了节省计算工作量，考虑到车站轴向长度较长，通常可以考虑将其简化为二维平面应变问题。然而，平面二维模型无法充分反应车站结构的实际情况，如对梁、柱和板的准确模拟。本文截取地铁车站典型的一段(8 m)，如图4所示，建立准三维有限元模型，通过约束模型轴向自由度，以使其符合真实情况。

图4　计算模型立面截取示意图 Fig.4 Analyticmodel interception

分析建模选用通用有限元软件ABAQUS。考虑结构和土体的相互作用，土体尺寸水平方向取所关心区域的范围，即距车站外墙100 m。竖直方向取车站结构竖向尺寸的3倍，即距地面75 m。引入人工边界，以消除边界上波的反射影响。考虑到结构的对称性，取半结构计算，模型计算简图如图5所示。

图5　模型计算简图 Fig.5 Analytic model diagram

选用实体单元模拟车站结构和土体，杆单元模拟抗拔桩。对于叠合墙式方案，内衬墙和地下连续墙用绑定命令连为整体。对于复合墙式方案，内衬墙和地下连续墙间设法向接触连接。对于离壁墙式方案，内衬墙和地下连续墙完全分离，用弹簧阻尼器单元连接。

2.2土体参数

土体在地铁列车振动荷载作用下剪应变的范围一般在10-5~10-4之间，仍处在弹性应变范围内[6]。为此，在分析车站结构型式对地铁诱发环境振动的影响时，结构和土体统一采用线弹性力学模型。根据弹性波理论[7]，介质的弹性模量E，泊松比μ，剪切模量G，密度ρ及剪切波速vs间存在关系：

(1)

结合实际工程相关地质勘查报告资料，整理计算得到各土层土体的计算参数如表1所示。表中，弹性模量则根据式(1)逆推得到。

2.3人工边界

建模过程中截取了有限范围内的土体，与土体范围无限的实际情况不符。若直接将边界设为固定端，则振动产生的波会在固定边界上产生反射，使计算分析结果失真。通过在边界上设置人工边界，可消除反射现象，确保分析模型和结果与实际相吻合。

表1　土层计算参数

表2　一致黏弹性人工边界参数

(2)

(3)

(4)

式(2)~(4)中，h为单元厚度(h=5 m)；G为土的剪切模量；ρ为土体密度；vs和vp为土的P波和S波波速；R为波源至人工边界的距离；αN和αT为法向与切向黏弹性人工边界修正系数(αN=4/3，αT=2/3)；α=αN/αT。

2.4输入荷载

为使输入荷载的特性更接近实际情况，模型选用同类场地地铁车站列车通过时实测的道床加速度时程记录作为输入荷载作用在模型对应的道床位置。即假设列车荷载为作用在道床表面的沿轨道方向无限长同相位振动[10]。由于本文主要考察不同车站结构型式对地铁诱发环境振动向外传播的影响，这一假定用于不同方案的对比是合理有效的。

实测加速度记录的时程曲线如图6所示；相应傅里叶谱曲线如图7所示。由图7知，加速度输入的卓越频率集中在40~140 Hz。

根据我国规范[11]，通常使用Z振级评价地铁诱发的环境振动，其定义如下：

(5)

式中，VLz为Z振级(dB)；aw为振动计权加速度有效值(m/s2)；a0为基准加速度(a0=10-6m/s2)。

按式(5)计算得输入的实测道床表面加速度Z振级为94.8 dB。

图6　输入加速度时程曲线 Fig.6 Time history of input acceleration

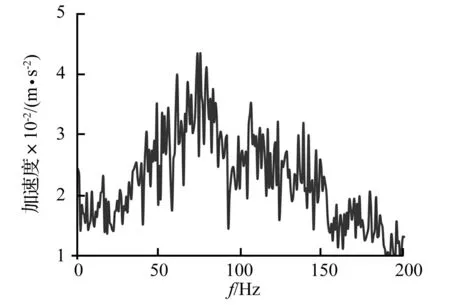
图7　输入加速度傅里叶谱 Fig.7 Fourierspectrum of input acceleration

2.5计算方法及阻尼

由于模型中存在接触问题，属于非线性模型，计算分析时应采用直接积分法。动力分析采用瑞利阻尼形成阻尼矩阵。瑞利阻尼的两个参数由下式确定[7]。

(6)

(7)

式(6)~(7)中，ζ0为阻尼比，ω1和ω2为所关心频段对应的上下限圆频率。

确定参数α和β后，任意一阶模态阻尼比可由下式计算得到。

(8)

式中，ω为模型的模态频率。

现有研究成果表明，当软土的剪应变在10-5~10-4范围时，其阻尼比约为0.02~0.05[12]。由于地铁引起的环境振动存在较多的高频成分，若取模型前几阶模态频率作为ω1和ω2计算瑞利阻尼参数，则由式(8)可知，高阶模态频率对应的模态阻尼将远高于低阶频率对应的模态阻尼，振动的高频分量会因此过早衰减，这与实际情况不符。

根据2.4节中输入荷载的频谱规律，取模型的基频2.4 Hz及荷载的卓越频率上限140 Hz作为ω1和ω2，取ζ0=0.05，得到瑞利阻尼参数：α=1.48，β=1.12×10-4这种取值方法保证了关心频段内模型的阻尼比处在合理的范围内。

3计算结果分析

3.1控制点选取

为考察对比不同车站结构型式对地铁诱发环境振动向外传播的影响，同时为方便地铁运营后做进一步测量验证，选取地表平面车站正上方处、地下连续墙后及目标建筑物室外地坪处作为控制点，如图8所示。图中控制点1距控制点2水平距离为13 m，控制点2距控制点3水平距离为50 m。

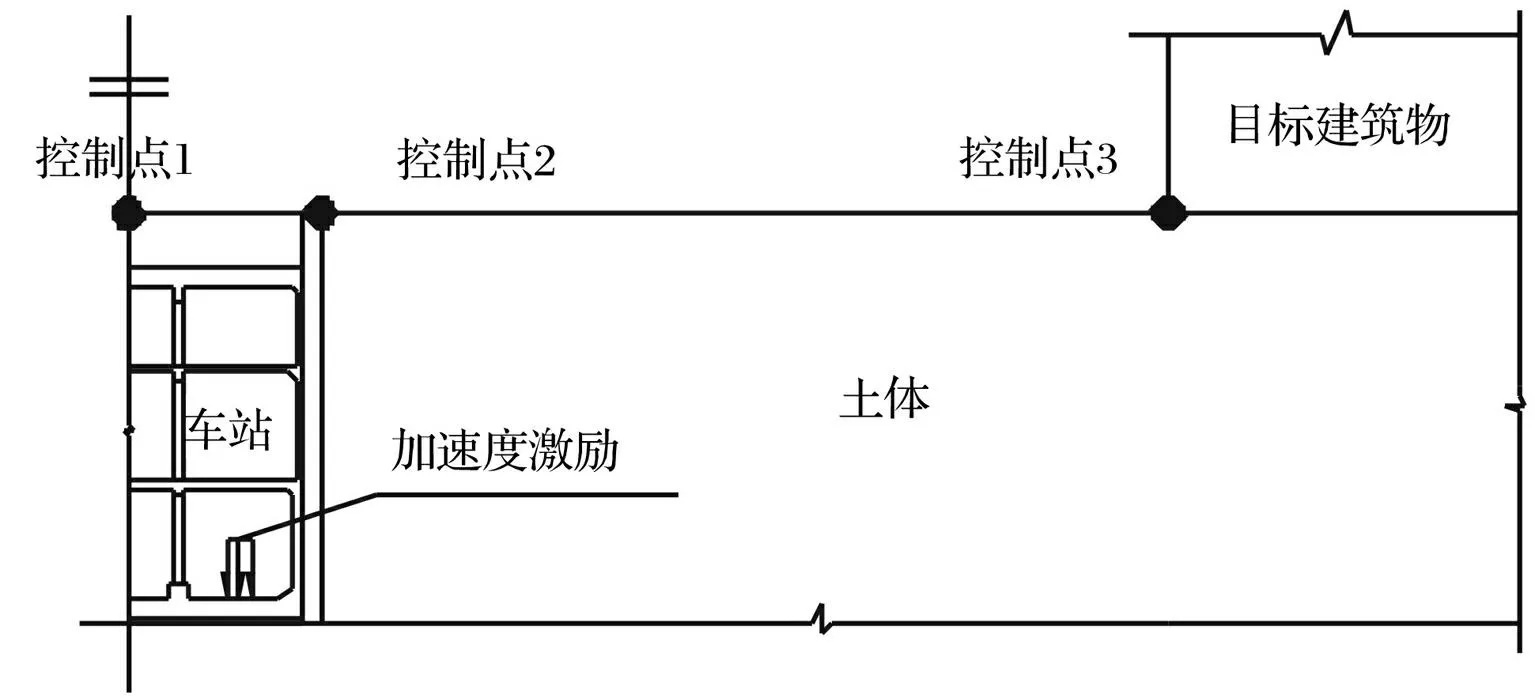
图8　控制点布置图 Fig.8 Distribution of control points

3.2时域结果及分析

计算得到实测竖向加速度作用下三种车站方案模型的加速度时程反应。三个控制点的加速度反应时程曲线如图9至图11所示(图中DHQ、FHQ、LBQ分别代表叠合墙式、复合墙式、离壁墙式车站方案的分析结果，下同)。

由图9至图11可知，采用离壁墙式车站方案时，地铁诱发振动的加速度峰值在控制点2和控制点3处最小，其次为复合墙式车站，叠合墙式车站最大。这说明车站内墙和外墙的分离可以有效地阻隔振动向外传播。控制点1处的加速度反应表明：离壁墙式和复合墙式车站由于有抗拔桩与压梁的存在，车站结构上部的振动加速度幅值与叠合墙式车站方案接近。

图9 控制点1加速度反应时程曲线Fig.9TimehistoryofaccelerationresponseatPoint1图10 控制点2加速度反应时程曲线Fig.10TimehistoryofaccelerationresponseatPoint2图11 控制点3加速度反应时程曲线Fig.11TimehistoryofaccelerationresponseatPoint3

3.3频域结果及分析

为进一步分析计算结果在频域中所揭示的规律，计算3个控制点的1/3倍频程谱，其结果如图12至图14所示。

由图12可知，车站正上方控制点1处，各车站方案振动卓越频率集中在15-30 Hz，当采用复合墙式车站方案时，各频率分量的幅值最小，离壁墙式车站次之，叠合墙式车站总体较大。

由图13可知，当振动传播至外墙后面控制点2时，5-10 Hz及15-30 Hz频段分量都明显衰减，卓越频率集中在2-3 Hz及15-30 Hz频段。离壁墙式方案车站地面振动大部分频率分量幅值已小于其他两个方案。

由图14可知，当振动传播至控制点3时，10 Hz以后的频率分量已大幅衰减，振动的卓越频率集中在2-8 Hz，其中2-3 Hz段和6-8 Hz段各有一波峰，前者峰值更大。此时，当采用离壁墙式车站方案时，各频率分量的幅值最小，复合墙式车站次之，叠合墙式车站最大。

图12 控制点1加速度反应1/3倍频程加速度谱Fig.121/3octavespectrumofaccelerationresponseofPoint1图13 控制点2加速度反应1/3倍频程加速度谱Fig.131/3octavespectrumofaccelerationresponseofPoint2图14 控制点3加速度反应1/3倍频程加速度谱Fig.141/3octavespectrumofaccelerationresponseofPoint3

从图12至图14还可以看出：随控制点距离的增加地表振动衰减非常明显，但相对于低频区域，振动在高频区域的衰减更加显著，地面振动的卓越频率逐渐前移。

3.4振动衰减规律及对比分析

三种车站方案在地表的加速度反应峰值随距离的衰减曲线如图15所示。由图中可知，地表振动加速度反应峰值随距离增加衰减明显，但在20 m和50 m附近都出现了轻微反弹(振动幅值随距离增加而略微增大)。对比三种车站方案的衰减曲线，可以发现从减小振动的角度看，采用离壁墙式方案时，地铁诱发的环境振动最小，复合墙式车站次之，叠合墙式车站总体最大。这说明分离车站结构内衬墙和地下连续墙对减小地铁所诱发的环境振动具有很好效果。

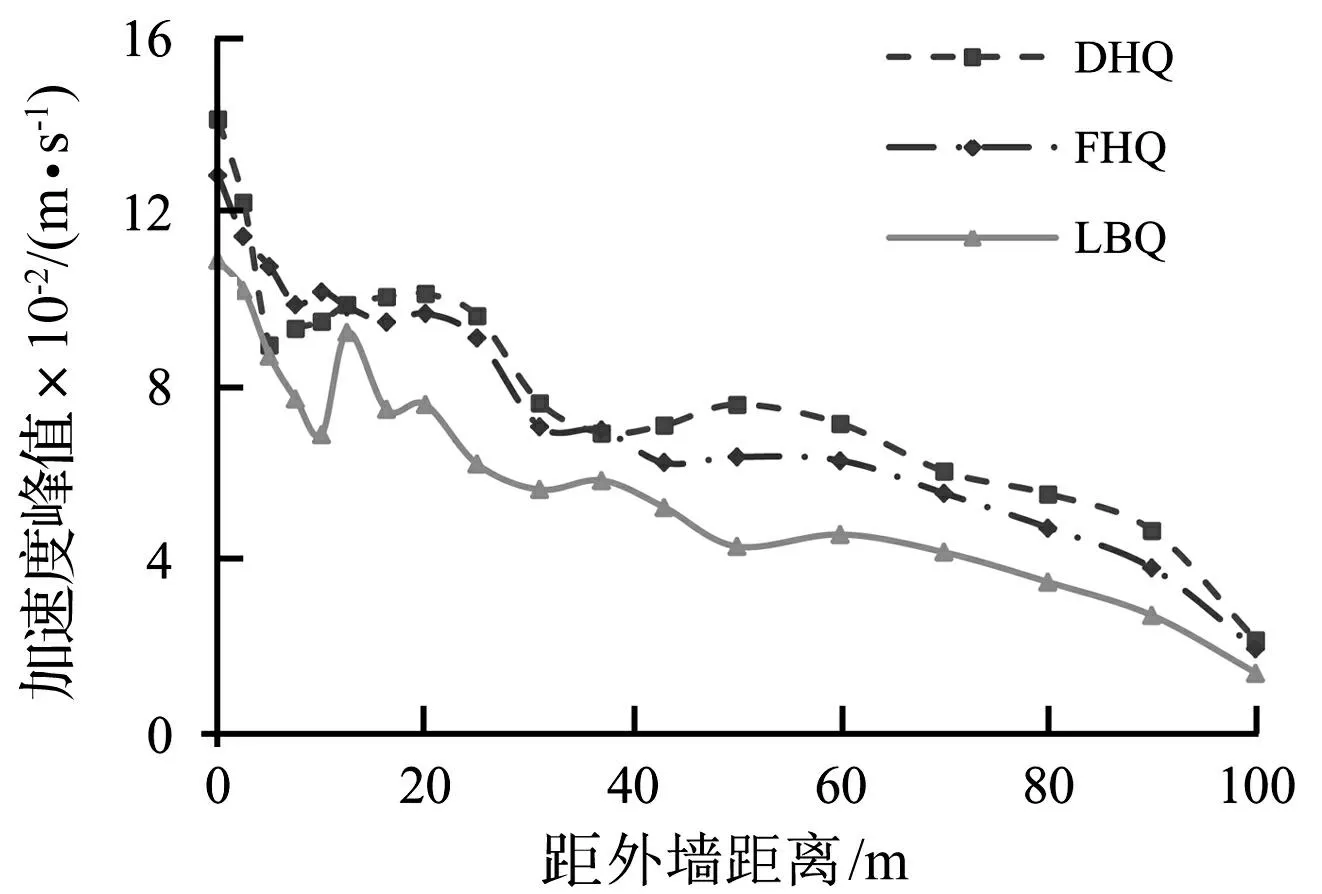
图15　加速度峰值衰减曲线 Fig.15 Attenuation curve of peak acceleration

为进一步研究离壁墙式和复合墙式车站方案的减振效果，考虑到目前常见的车站型式为叠合墙式，以叠合墙式车站对应振动量值为参考标准，按下式定义振动计权加速度有效值减振效果系数d1和振动加速度峰值减振效果系数d2：

(9)

式中，aw为振动计权加速度有效值；aw0为叠合墙式方案振动计权加速度有效值。

(10)

式中，ap为振动加速度峰值；ap0为叠合墙式方案振动计权加速度有效值。

按照式(9)和式(11)计算得到复合墙式和离壁墙式车站方案在地表距离外墙0 m、25 m、50 m和100 m的减振系数d1和d2，结果列于表3。由表3知，与叠合墙式车站相比，复合墙式车站对振动计权加速度有效值和加速度峰值的最佳减振效果分别达到了26%和16%，相应离壁墙式车站的最佳减振效果则分别达到了46%和32%。车站型式对地铁诱发的环境振动有明显的影响，其中离壁墙式车站方案的减振效果最好，为最佳方案。

表3　减振效果系数

4结论

本文对地铁车站考虑地铁运行诱发环境振动的数值建模方法进行了系统研究，以某拟建地铁车站为工程背景，建立了车站—土的准三维有限元模型，计算分析了不同车站结构形式下地铁所诱发的环境振动的传播衰减规律，得到的主要结论如下：

(1)采用离壁墙式车站方案，地下连续墙外地铁所诱发环境振动的加速度反应峰值和Z振级最小，复合墙式车站次之，叠合墙式车站最大。

(2)地铁所诱发的环境振动在传播一定距离后，其高频分量迅速衰减，振动卓越频率集中在2-8 Hz，且采用离壁墙式车站方案，环境振动的各频率分量最小，复合墙式车站次之，叠合墙式车站最大。

(3)分离地铁车站结构内衬墙和外围地下连续墙对减小地铁所诱发的环境振动向外传播具有较好的效果。对于环境振动水平需要严格控制的地区，地铁车站可选用离壁墙式结构方案。

参考文献

[1]洪俊青, 刘伟庆. 地铁对周边建筑物振动影响分析[J]. 振动与冲击，2006, 25(4): 142-145.

HONG Jun-qing, LIU Wei-qing. Analysis of effects induced by subway train on surrounding building vibration[J]. Journal of Vibration and Shock, 2006, 25(4): 142-145.

[2]Hung H H, Yang Y B. A review of researches on ground-borne vibrations with emphasis on those induced by train[J]. Proceeding of the National Science Council, ROC(A), 2001, 25(1): 1-16.

[3]Gupta S, Stanus Y, Lombaert G, et al. Influence of tunnel and soil parameters on vibrations from underground railways[J]. Journal of Sound and Vibration, 2009, 327: 70-91.

[4]辜小安, 任京芳, 刘扬,等. 我国地铁环境振动现状及控制措施[J]. 铁道劳动安全卫生与环保, 2003, 30(5): 206-208.

GU Xiao-an, REN Jing-fang, LIU Yang, et al. The status quo of environment vibration level and control measures of subway in China[J]. Railway Occupational Safety Health & Environmental Projecion, 2003, 30(5): 206-208.

[5]田春芝. 地铁振动对周围建筑物影响的研究概况[J]. 铁道劳动安全卫生与环保, 2000, 27(1): 64-67.

TIAN Zhi-chun. Influence of subway vibration on surroun-ding buildings[J]. Railway Occupational Safety Health & Environmental Projecion, 2000, 27(1): 67-70.

[6]周萌, 韦凯, 周顺华,等. 轨道型式对地铁与建筑共建结构振动响应的影响[J]. 中国铁道科学, 2011, 32(2): 33-40.

ZHOU Men, WEI Kai, ZHOU Shun-hua, et al. Influence of different track types on the vibration response of Jointly-Built Structure of Subway and the Buildings[J].China Railway Science, 2011, 32(2): 33-40.

[7]胡聿贤. 地震工程学[M]. 北京: 地震出版社, 2006.

[8]方志. 土-结构相互作用体系人工边界的动力反应与分析[J]. 力学季刊, 2009, 30(3): 475-480.

FANG Zhi. Dynamic response and artificial boundary analysis in soil structure interaction system[J]. Chinese Quarterly of Mechanics, 2009, 30(3): 475-480.

[9]刘晶波, 谷音, 杜义欣. 一致黏弹性人工边界及黏弹性边界单元[J]. 岩土工程学报, 2006, 28(9): 1070-1075.

LIU Jing-bo, GU Yin, DU Yi-xin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1070-1075.

[10]孟宪春, 景立平, 孙海峰. 地铁运行对地面环境的振动影响[J]. 世界地震工程, 2010, 26:310-314.

MENG Xian-chun, JING Li-ping, SUN Hai-feng. Ground vibration induced bymetro running[J]. World Earthquake Engineering,2010, 2010, 26:310-314.

[11]城市区域环境振动标准(GB 10070-88) 及城市区域环境振动测量方法(GB 10071-88) [S]．中华人民共和国国家标准.

[12]白玉, 余湘娟，高磊.南京地区粉质粘土动剪切模量与阻尼比试验研究[J]. 水利与建筑工程学报, 2013, 11(1): 27-30.

BAI Yu, YU Xiang-juan, GAO Lei. Experimental study on dynamic shear modulus and damping ratio of silty clay soil in nanjing[J]. Journal of Water Resources and Architec-ture Engineering, 2013, 11(1): 27-30.