RC柱对串联隔震体系水平刚度影响研究

2016-01-04吴忠铁,杜永峰,李慧

合肥工业大学学报（自然科学版） 2015年1期

关键词：有限元分析

杜永峰(1962-),男,甘肃正宁人,博士,兰州理工大学教授,博士生导师;

李慧(1954-),女,甘肃天水人,兰州理工大学教授,博士生导师.

RC柱对串联隔震体系水平刚度影响研究

吴忠铁1,2, 杜永峰2,李慧2

(1.西北民族大学土木工程学院,甘肃兰州730050; 2.兰州理工大学防震减灾研究所,甘肃兰州730050)

摘要:为了研究RC柱对串联隔震体系水平刚度的影响,文章以串联隔震体系及其构件的水平刚度方程为基础,基于假定提出了串联隔震体系刚度的简化方程;以橡胶支座基本设计荷载和常用参数为依据,主要分析了RC柱的轴压比和高宽比对构件自身及整体水平刚度的影响;并与三组串联隔震体系的有限元分析数据进行对比,结果表明了公式的正确性和适用性。

关键词:串联隔震体系;水平刚度;简化方程;轴压比;高宽比;有限元分析

基金项目：国家自然科学基金资助项目(51178211);西北民族大学引进人才科研资助项目(xbmuyjrc201405)

作者简介：吴忠铁(1982-),男,黑龙江绥化人,博士,西北民族大学副教授;

doi:10.3969/j.issn.1003-5060.2015.01.017

中图分类号:TU352.12文献标识码：A

EffectofRCcolumnonhorizontalstiffnessofserialisolationsystem

WUZhong-tie1,2,DUYong-feng2,LI Hui2

(1.SchoolofCivilEngineering,NorthwestUniversityforNationalities,Lanzhou730050,China; 2.InstituteofEarthquakeProtectionandDisasterMitigation,LanzhouUniversityofTechnology,Lanzhou730050,China)

Abstract:In order to study the effect of reinforced concrete(RC) column on the horizontal stiffness of serial isolation system, and on the basis of the serial isolation system and the calculation formula of horizontal stiffness of laminated rubber bearing and column, the simplified calculation formula of the stiffness of serial isolation system is proposed based on the assumptions. According to the basic design loads and the common parameters of the laminated rubber bearing, the effect of axial compression ratio and aspect ratio of RC column on the components and the serial isolation system is studied respectively and compared with the data of three groups of finite element models. The results show that the calculation formula is correct and applicable.

Keywords:serialisolationsystem;horizontalstiffness;simplifiedcalculationformula;axialcompressionratio;aspectratio;finiteelementanalysis

串联隔震体系已经在隔震结构中大量应用,常见于将隔震支座置于首层柱顶或地下室顶,其特点是把叠层橡胶支座和钢筋混凝土柱组成的串联隔震体系作为隔震结构的隔震层。国内外专家学者对于橡胶支座的力学性能进行了广泛的理论研究和试验研究,提出了一些线性和非线性的计算模型,并对于不同状态下橡胶支座的稳定性和水平刚度进行了研究[1-9]。而对于串联隔震体系的研究相对较少,串联RC柱的串联隔震体系的力学性能变化值得关注和研究。文献[10]首先对串联隔震体系水平刚度系数进行了理论分析,探讨了临界荷载公式；文献[11-15]采用微分求积法对于串联隔震体系进了大变形理论分析、随机屈曲分析、模型的相关参数分析和缩尺试验;文献[16-17]对带串联隔震体系的隔震结构进行了动力测试和数值分析。本文推导了串联隔震体系中叠层橡胶支座的变形方程,给出钢筋混凝土柱的变形方程,求解了各构件的水平刚度和整体刚度方程,基于假定提出简化方程,主要分析了RC柱的高宽比和轴压比对水平刚度的影响,并与有限元模型进行了对比。

1理论分析与参数设定

根据文献[15]给出串联隔震体系的整体刚度方程和构件方程。

叠层橡胶支座的水平刚度KR(P)为:

(1)

钢筋混凝土柱的水平刚度KC为:

(2)

串联体系整体的水平刚度K(P)为:

(3)

其中

h为叠层橡胶支座的高度;ER为橡胶支座的弹性模量;IR为橡胶支座的截面惯性矩;GR为橡胶支座的剪切模量;AR为橡胶支座的截面面积;H为钢筋混凝土柱的高度,EC为钢筋混凝土柱的弹性模量;IC为钢筋混凝土柱的截面惯性矩;GC为钢筋混凝土柱的剪切模量;AC为钢筋混凝土柱的截面面积;μR和μC为截面形状系数;P为竖向荷载。

为了方便计算串联隔震体系整体刚度K(P),将(3)式解耦,忽略RC柱的二阶矩和剪切变形的影响,提出一种串联隔震体系刚度简化方程,即

(4)

其中,KSR(P0)=GRAR/h为普通橡胶支座竖向荷载P=0时的水平刚度;KC=3ECIC/H3。

将叠层橡胶支座视为等效均质柱,其等效抗弯刚度ERIR和抗剪刚度GRAR计算公式为:

(5)

(6)

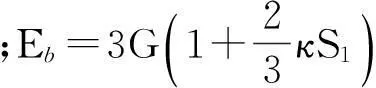
为了研究钢筋混凝土柱参数对于串联隔震体系及构件水平刚度的影响,设定钢筋混凝土柱的轴压比和高宽比分别表示为RN和RBC,叠层橡胶支座的高宽比为RBR,其计算公式为:

(7)

(8)

(9)

其中,p为叠层橡胶支座压力设计值,按照文献[18]甲、乙、丙类建筑分别可取10、12、15MPa;DC为方形柱的截面尺寸;fC为混凝土材料强度设计值。

上述各水平刚度方程中含有4个参数εR、εC、λR、λC,其计算公式为:

(10)

(11)

(12)

(13)

2数值分析与讨论

为了分析方便，选用文献[19]的叠层橡胶支座参数,详见表1所列。在进行隔震设计时选取叠层橡胶支座的原则是以竖向荷载为标准,按照叠层橡胶支座的竖向承载力来确定叠层橡胶支座的类型。根据文献[18],叠层橡胶支座根据建筑的类型(甲、乙、丙)竖向设计荷载依次对应10、12、15MPa。本文选择按照乙类建筑,竖向荷载为12MPa。因此,在选用某一类的叠层橡胶支座时,轴力与设计竖向荷载基本一致,根据叠层橡胶支座的直径和设计竖向荷载则可确定轴力。房屋建筑结构混凝土常用型号为C30,按文献[18],混凝土材料参数取fC=14.3MPa,EC=30GPa,υC=0.2。

表1　普通叠层橡胶支座不同D R下的相关参数

考虑混凝土柱高宽比的变化情况,对9种普通叠层橡胶支座在轴压比一定的条件下进行分析。

水平刚度比与RBC和DR三维变化关系如图1所示。图1中，K为串联隔震体系的水平刚度;KR为叠层橡胶支座的水平刚度;KC为钢筋混凝土柱的水平刚度;KSR为两端固定时叠层橡胶支座水平刚度;KS为由简化方程得到的串联隔震体系的水平刚度。

图1　水平刚度比与R BC和D R三维变化关系 (p=12 MPa)

柱与叠层橡胶支座串联的构件状态下,关于钢筋混凝土柱的抗震等级和设计要求,建筑抗震设计规范没有明确提出。对于串联隔震体系中柱抗震等级主要参考文献[19],其建议串联隔震体系中柱宜按悬臂柱进行计算,抗震等级宜按二级。根据文献[18]中表6.1.2确定框架柱的抗震等级,按照8度0.2g设防地区框架柱的等级应为一、二级,其隔震层下部结构应按罕遇地震下验算。而串联隔震体系的钢筋混凝土柱与框架柱的连接约束存在较大的差异性。因此,本文在进行分析时柱的轴压比按照抗震等级为一级取值,RN=0.65,隔震支座设计荷载按乙类建筑设计荷载值p=12MPa。

由图1可以看出,4种刚度比随着高宽比RBC的增大而减小,随着隔震支座的直径增大而增大,但从变化趋势来看,KR/KSR(P0)、KC/KSR(P0)和K/KSR(P0)受高宽比RBC的影响较大,而受叠层橡胶支座的类型影响不明显,所以可以按照常用一类隔震支座进行其他相关参数影响分析。图1d中,KS/K的值均在1以上,表明简化计算公式KS大于精细计算公式K值,当RBC在10以内时总体差值小于20%,当RBC在4以内时总体差值在7%以内;随着直径的增大,误差值更小,表明简化计算公式KS在低高宽比的情况下,具有足够的精度,能够满足工程需要。

以上分析表明叠层橡胶支座直径DR对于以上分析方法影响较小,故选用叠层橡胶支座直径DR=700mm的参数,进行设计荷载作用下钢筋混凝土柱的轴压比RN和高宽比RBC对串联隔震体系的水平刚度的影响分析。各水平刚度比(k)与RN和RBC变化关系如图2所示。

由图2a可知,在轴压比一定的情况下刚度比KSR/KSR(P0)、KR/KSR(P0)和K/KSR(P0)随着高宽比的变化情况,KSR/KSR(P0)的比值不受高宽比的影响,KR/KSR(P0)的比值随着高宽比的增大而降低。随着轴压比的不同,刚度比值降低的程度也不相同,随着轴压比的增大降低速度增大,轴压比RN在0.1～0.9内,高宽比RBC在0～10内,KR/KSR(P0)刚度比变化均小于10%；当高宽比RBC在0～4范围内，刚度比KR/KSR(P0)小于5%,此时隔震支座的刚度取固结时隔震支座的刚度进行计算。从K/KSR(P0)的变化可以看出,在轴压比一定的条件下,K/KSR(P0)值随着高宽比的增大而降低,轴压比越大降低的速度越快,图2a中当RN=0.1时降低的速度最慢,在RN=0.9时降低的速度最快。轴压比RN在0.1～0.9内和高宽比RBC在1～10内K/KSR(P0)值变化最大为30%,当高宽比RBC为1～3时K/KSR(P0)值变化在5%左右,可以按照叠层橡胶支座两端固定取值。

从图2b可以看出轴压比RN在0.1～0.9范围内KC/KSR(P0)随着RBC增大而降低,高宽比小于4时,不同的轴压比下KC/KSR(P0)还有一定的差别,随着高宽比的增大,差别越来越小,当高宽比达到10时,其值均小于10。

不同构件水平刚度比k与RN的变化关系如图3所示。

从图3a中可知,KSR/KSR(P0)、KR/KSR(P0)和K/KSR(P0)在给定的高宽比RBC下,随着轴压比RN的增大,各刚度比值在降低,且随着高宽比RBC的增大,降低的趋势增大,在给定轴压比范围内,叠层橡胶支座的水平刚度变化范围均值在10%以内,而整体刚度的变化在26%以内,显然,刚度的变化不容忽视;而当高宽比RBC<5时,整体刚度变化小于10%;高宽比RBC≤3.5时,整体刚度的变化均为5%左右,此时可按两端固定的叠层橡胶支座刚度取值。从图3b可以看出,在一定的高宽比时,KC/KSR(P0)随着轴压比的增大而降低,当高宽比较小时降低相对明显,而当高宽比较大时变化相对平缓。

简化水平刚度方程KS/KSR(P0)和精细水平刚度方程K/KSR(P0)与RN和RBC的三维变化关系如图4所示,KS/K与RN和RBC的三维变化关系如图5所示。

图2　不同构件水平刚度比k与R BC的变化关系

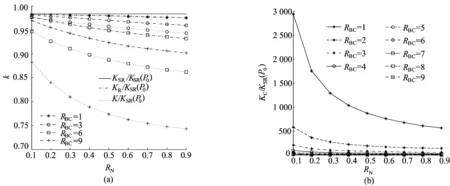
图3　不同构件水平刚度比k与R N的变化关系

从图4可以看出,KS/KSR(P0)和K/KSR(P0)变化趋势基本一致,KS/KSR(P0)值比K/KSR(P0)值大,结合图5可知轴压比RN在0.1～0.9和高宽比RBC在1～10之间时KS/K值在1~1.08以内,可知简化方程与原方程计算的水平刚度误差在8%以内，表明简化刚度方程具有足够的精度。

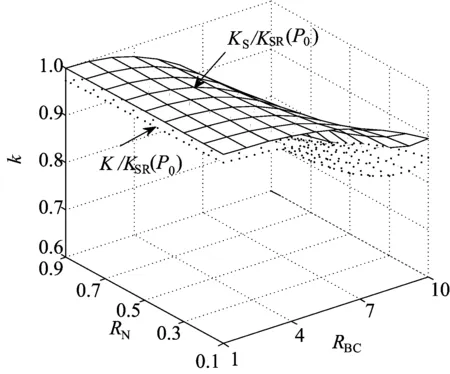
图4　水平刚度比k与R BC和R N三维变化关系

图5　K/K S与R BC和R N三维变化关系

3理论模型与有限元模型对比分析

为了表明上述理论分析模型具有一定的代表性,随机建立了3类串联隔震体系模型,进行有限元分析。用有限元结果与精细模型和简化模型的计算结果进行了对比,给出了整体等效刚度与单独橡胶支座等效刚度对比图,如图6所示,其中实线为理论计算公式曲线。

图6中,虚线为有限元模型分析曲线,分别为KeqFEA90、KFEA90和KFEA500。其中,KeqFEA90为串联直径90mm铅芯橡胶支座的串联隔震体系,竖向应力为4MPa;KFEA90和KFEA500为串联直径90mm和500mm普通橡胶支座的串联隔震体系,竖向应力分别为4MPa和12MPa。建模过程和相关材料参数参照文献[14]。

从图6可以看出,5条曲线变化趋势基本一致,低高宽比时3组有限元刚度比曲线均与简化模型较为接近,随着高宽比的增大,KeqFEA90和KFEA500有限元刚度比曲线远离简化模型,逐渐接近精细模型。从整个曲线的变化情况来看,KFEA90和KFEA500的刚度比曲线均在精细模型和简化模型附近变化,误差值均在5%以内,基本一致,而KeqFEA90的刚度比曲线变化幅度相对较大,当高宽比大于8时,其值均比精细模型和简化模型的刚度比曲线低,当高宽比为10时刚度比分别低了5%和10%左右。理论分析结果和有限元分析较为接近,表明了精细模型和简化模型的正确性与合理性。

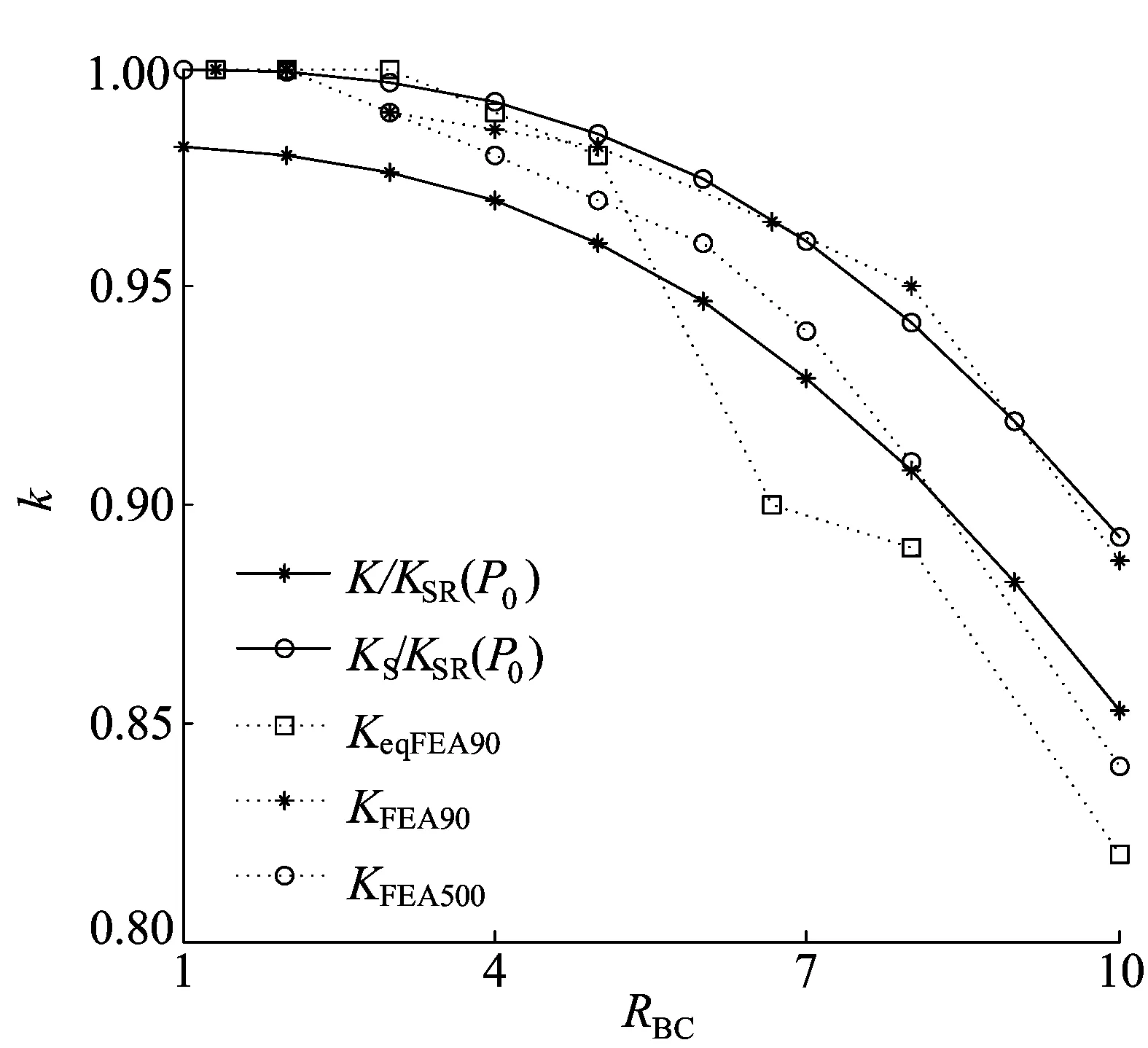
图6　理论分析和有限元分析对比

4结论

(1)RC柱对串联隔震体系的刚度影响明显,可以根据高宽比和轴压比进行控制分析。

(2) 在常规的轴压比和高宽比下,串联隔震体系的水平刚度简化方程与原方程的误差在8%以内,具有一定的适用性。

(3) 当高宽比小于等于3.5时,串联隔震体系刚度可用叠层橡胶支座的水平刚度替代计算。

(4) 理论模型和有限元模型曲线变化基本一致,表明了理论模型的正确性。

[参考文献]

[1]ImbimboM,KellyJM.Stabilityofisolatorsatlargehorizontaldisplacements[J].EarthquakeSpectra, 1997, 13(3):415-430.

[2]KellyJM,MarsicoMR.Stabilityandpost-bucklingbehaviorinnonboltedelastomericisolators[J].SeismicIsolationProtectSyst, 2010,1(1):41-54.

[3]IizukaM.Amacroscopicmodelforpredictinglarge-deformationbehaviorsoflaminatedrubberbearings[J].EngineeringStructures,2000,22(4):323-334.

[4]AminAFMS,WiragunaSI,BhuiyanAR.Hyperelasticitymodelforfiniteelementanalysisofnaturalandhighdampingrubbersincompressionandshear[J].JournalofEngineeringMechanics,2006,132(1):54-64.

[5]RavariAK. P-Δandendrotationeffectsontheinfluenceofmechanicalpropertiesofelastomericisolationbearings[J].JournalofStructuralEngineering,2012,138:669-675.

[6]刘文光,周福霖,庄学真.柱端隔震夹层橡胶垫力学性能试验研究[J].地震工程与工程振动,1999, 19(3):121-126.

[7]张敏政,孟庆利,裴强.叠层橡胶隔震支座的动态稳定性和力学特性研究[J].地震工程与工程振动,2002,22(5):87-91.

[8]杨巧荣,庄学真,刘文光,等.夹层橡胶隔震支座全刚性性能、回转刚性及高压缩应力性能试验研究[J].地震工程与工程振动,2000,20(4):118-125.

[9]杜永峰, 吴忠铁, 范萍萍.端部固定转角对叠层橡胶支座水平刚度影响分析[J].合肥工业大学学报:自然科学版,2013,36(12):1489-1494.

[10]周锡元,韩淼.橡胶支座与R/C柱串联隔震系统水平刚度系数[J].振动工程学报,1999,12(2):159-165.

[11]杜永峰,李慧.叠层橡胶垫与RC柱串联隔震体系的随机屈曲分析[J].防灾减灾工程学报,2010,30(Z1):16-21.

[12]杜永峰,朱前坤,李慧.串联隔震体系的大变形力学行为分析与试验[J].振动与冲击,2011,30(11):236-239.

[13]杜永峰,林治丹,李慧.橡胶支座与柱串联体系的动力特性分析[J].振动与冲击,2012,31(17):134-138.

[14]杜永峰,吴忠铁.考虑初始位移的串联隔震体系竖向承载力有限元分析[J].土木工程学报,2012,45(2):128-132.

[15]杜永峰,吴忠铁.串联隔震体系水平刚度的参数研究[J].振动与冲击,2013,32(23):68-73.

[16]吴应雄,祁皑,颜学渊.某首层柱顶隔震结构动力特性测试研究[J]. 地震工程与工程振动,2011,31(6):147-152.

[17]马长飞,谭平,周福霖.近场地震作用下考虑Ρ-Δ效应的首层柱顶隔震结构地震反应分析[J].振动工程学报,2012,25(4):439-445.