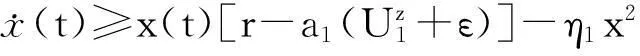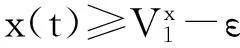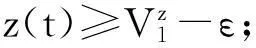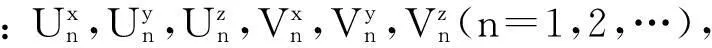一类捕食者具有阶段结构的时滞捕食模型的稳定性分析

段复建(1965-),女，黑龙江黑河人，博士，桂林电子科技大学教授，硕士生导师.

一类捕食者具有阶段结构的时滞捕食模型的稳定性分析

袁媛1,段复建2

(1.桂林航天工业学院 理学部,广西 桂林541004; 2.桂林电子科技大学 数学与计算科学学院,广西 桂林541004)

摘要:文章考虑捕食者具有阶段结构的时滞捕食模型,通过研究模型雅克比矩阵的特征方程得到所有非负平衡点的局部稳定性,并得到Hopf分支存在性的充分条件;利用比较原理并构造Lyapunov函数得到边界平衡点的全局稳定性;运用迭代方法与比较原理得到正平衡点的全局渐近稳定的充分条件。

关键词:阶段结构;时滞;捕食模型;全局稳定性;Hopf分支

收稿日期：2013-12-27；修回日期：2014-04-10

基金项目：广西自然科学基金资助项目(2011GXNSFA018138);广西高校科研资助项目(LX2014469)

作者简介：袁媛(1982-),女，四川自贡人，桂林航天工业学院讲师;

doi:10.3969/j.issn.1003-5060.2015.01.030

中图分类号:O29 文献标识码：A

Stabilityanalysisofadelayedpredator-prey

modelwithstagestructureforpredator

YUANYuan1,DUAN Fu-jian2

(1.FacultyofScience,GuilinUniversityofAerospaceTechnology,Guilin541004,China; 2.SchoolofMathematicsandComputingScience,GuilinUniversityofElectronicTechnology,Guilin541004,China)

Abstract:A delayed predator-prey model with stage structure for predator is considered. By studying the characteristic equation of the Jacobian matrix, the local stability of all the non-negative equilibria is obtained as well as the sufficient conditions for the existence of Hopf bifurcation. And by using comparison arguments and Lyapunov functions, the global stability of the boundary equilibrium is investigated. Moreover, the sufficient conditions of the global asymptotic stability of the positive equilibrium are derived by using iteration technique and comparison arguments.

Keywords:stagestructure;timedelay;predator-preymodel;globalstability;Hopfbifurcation

0引言

捕食者-食饵模型是种群动力学中的基本模型,通常研究者假设所有的捕食者具有捕食能力和生育能力,这对大多数物种来说是不现实的。实际上,很多物种在成长过程中至少要经历2个阶段:幼年和成年。因此近年来考虑食饵或捕食者具有阶段结构的捕食模型备受关注[1-6]。但是大多数捕食者在捕食食饵时是不管食饵年龄大小的,而捕食者在不同的年龄段生理机能如捕食率、繁殖率等有很大的差异,因此在捕食模型中考虑捕食者的阶段结构具有现实意义。

另一方面,捕食者捕食食饵后并不会立即转化为自身的营养,需要一段时间才能转化,即存在时滞。一般地,时滞微分方程比常微分方程有更复杂的动力学行为,因为一个时滞能引起稳定的平衡点变得不稳定,并能引起捕食系统出现周期振荡的现象。文献[7]提出了具有捕食时滞和消化时滞的食饵具有阶段结构的捕食模型,通过研究得到了非负平衡点的局部与全局稳定性、Hopf分支的存在性等充分条件。

基于上述思想,本文改进文献[8]的捕食者具有阶段结构的时滞捕食模型,假设捕食者分为幼年与成年两类,成年捕食者具有捕食能力,成年捕食者捕食食饵后一方面会降低食饵种群的增长率,另一方面通过消化转化为自身的营养用于自身成长与繁殖后代,为此引入捕食时滞和消化时滞,具体模型如下:

(1)

在模型(1)式中,y(t)、z(t)分别为t时刻食饵、幼年捕食者、成年捕食者的密度;r为食饵种群的内禀增长率;η1、η2为食饵、成年捕食者的种内竞争率;d1、d2为幼年捕食者与成年捕食者的死亡率;c为捕食者从幼年个体向成年个体的转化率;a1为成年捕食者的捕食率;a2/a1为成年捕食者转化为自身营养用于繁殖的转化率;τ1为捕食时滞, 即单位时间内成年捕食者需要经过τ1的时滞才具有降低食饵种群平均增长率的能力;τ2为成年捕食者捕食食饵后需要消化为自身营养的时滞。以上参数都是正常数。

模型(1)式的初始条件为:

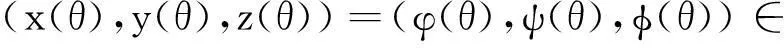
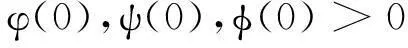
(2)

1局部稳定性与Hopf分支

当a2rc>η1d2(d1+c)时,正平衡点E*(x*,y*,z*)存在。

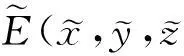
(3)

在E0(0,0,0)处,特征方程(3)式简化为：

可见一个正实根为λ1=r>0,其余2个根为负实数,故E0(0,0,0)总是不稳定的。

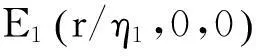
其中,λ1=-r<0;λ2+λ3<0;λ2λ3=d2(d1+c)-a2rc/η1。故当η1d2(d1+c)>a2rc时,E1(r/η1,0,0)是局部渐近稳定的, 当η1d2(d1+c)

在E*(x*,y*,z*)处,(3)式简化为:

(4)

其中,τ=τ1+τ2;p2=η1x*+d1+c+d2+2η2z*>0;p1=η1x*(d1+c+d2+2η2z*)+η2z*(d1+c)>0;p0=η1η2(d1+c)x*z*>0;q0=a1a2cx*z。

当τ=0时,特征方程为λ3+p2λ2+p1λ+(p0+q0)=0,显然,p0+q0>0,p2>0均成立。经计算有:

因此由Routh-Hurwitz定理可知:当τ=0时,如果η1η2(d1+c)>a1a2c成立,E*是局部渐近稳定的。

当τ>0时,设iω(ω>0)是方程(4)式的一个根,则iω满足等式, 代入分离实部与虚部得到:

(5)

(5)式中2个等式平方后相加得:

(6)

经过简单计算有:

进一步, 对(4)式左右两边关于τ求导,得到:

解出：

因此有：

于是,总结以上的论证过程有定理1。

定理1对模型(1)式来说, 有如下结论:

(1) E0(0,0,0)总是不稳定的。

(2) 当η1d2(d1+c)>a2rc时,E1(r/η1,0,0)是局部渐近稳定的; 当η1d2(d1+c)

2全局稳定性

引理1模型(1)式满足初始条件(2)式的解都是非负的。

引理2考虑模型:

(7)

有如下结论:

(1) 当η1d2(d1+c)>a2rc时, 模型(7)式的平衡点(0,0)是全局渐近稳定的。

(2) 当η1d2(d1+c)

证明经计算(7)式的雅克比矩阵的特征方程容易得到: 当η1d2(d1+c)>a2rc时, (0,0)是唯一的非负平衡点且是局部渐近稳定的,进而是全局渐近稳定的;当η1d2(d1+c)

定义Lyapunov函数如下：

其中，k1=1;k2=a2rv*/(η1cu*)。

沿着模型(7)式的任意解,V(t)对t求导:

即

(8)

(8)式等号成立当且仅当u=u*,v=v*。由文献[9]中定理6.3可知, 所有的解都趋近于最大的不变子集{V′(t)=0}。因此, 由LaSalle不变性原理可得(u*,v*)是全局渐近稳定的。

定理2如果η1d2(d1+c)>a2rc成立, 则边界平衡点E1(r/η1,0,0) 是全局渐近稳定的。

考虑模型(1)式中后2个等式的辅助系统:

(9)

定理3如果η1d2(d1+c)a1a2c成立,则E*是全局渐近稳定的。

由引理2与比较原理可知,

因为ε充分小,所以有：

对充分小的ε>0, 当 t>T2+τ2时,模型(1)式的后2个方程变为:

由引理2与比较原理可得：

因为ε>0充分小, 所以有：

心理数字线假说的最大特点：强调数量表征的先天性，独立于言语，与空间注意有关。大脑不同区域具有功能特异性，顶叶皮层主要参与空间注意、空间工作记忆、视空搜索等任务。如果数量任务能同样激活顶叶皮层区域兴奋，就可以建立数量表征与空间知觉神经机制上的关联。

通过比较论证得:

对充分小的ε>0, 当t>T4+τ1时, 模型(1)式的后2个方程有如下形式:

由引理2和比较原理可得：

因为ε>0充分小, 所以有：

(10)

[参考文献]

[1]XuRui,ChaplainMAJ,DavidsonFA.Persistenceandglobalstabilityofaratio-dependentpredator-preymodelwithstagestructure[J].AppliedMathematicsandComputation，2004,158(3):729-744.

[2]LiFeng,LiHongwei.Hopfbifurcationofapredator-preymodelwithtimedelayandstagestructurefortheprey[J].MathematicalandComputerModelling,2012,55(3/4):672-679.

[3]XuRui.Globaldynamicsofapredator-preymodelwithtimedelayandstagestructurefortheprey[J].NonlinearAnalysis:RealWorldApplications,2011,12(4):2151-2162.

[4]ChakrabortyK,JanaS,KarTK.Globaldynamicsandbifurcationinastagestructuredprey-predatorfisherymodelwithharvesting[J].AppliedMathematicsandComputation, 2012, 218(18): 9271-9290.

[5]FuShengmao,ZhangLina,HuPing.GlobalbehaviorofsolutionsinaLotka-Volterrapredator-preymodelwithprey-stagestructure[J].NonlinearAnalysis:RealWorldApplications, 2013,14(5): 2027-2045.

[6]HuHaijun,HuangLihong.StabilityandHopfbifurcationinadelayedpredator-preysystemwithstagestructureforprey[J].NonlinearAnalysis:RealWorldApplications, 2010, 11(4): 2757-2769.

[7]苗宝军，李雪臣.具混合边界条件的捕食模型正稳态解的存在性[J].合肥工业大学学报：自然科学版，2013，36(4)：491-497.

[8]KarTK,JanaS.Stabilityandbifurcationanalysisofastagestructuredpredatorpreymodelwithtimedelay[J].AppliedMathematicsandComputation,2012,219(8):3779-3792.

[9]LaSalleJP. 动力系统的稳定性[M]. 陆征一,译.成都:四川科学技术出版社, 2002:37.

(责任编辑张镅)