环F2m+uF2m上常循环码及其Gray像

开晓山(1975-),男,安徽青阳人,博士,合肥工业大学副教授,硕士生导师.

环F2m+uF2m上常循环码及其Gray像

张付丽1,开晓山1,陈安顺2

(1.合肥工业大学 数学学院,安徽 合肥230009; 2.滁州学院 数学科学学院,安徽 滁州239000)

摘要:文章研究了环F2m+uF2m上的循环码与(1+u)-常循环码之间的关系,其中u2=0。利用F2m+uF2m到的Gray映射,确立了F2m+uF2m上(1+u)-常循环码的Gray像,由此证明了F2m+uF2m上奇长度的循环自对偶码是类型Ⅰ码。

关键词:(1+u)-常循环码;循环码;Gray映射;自对偶码;类型Ⅰ码

收稿日期：2013-12-05

基金项目：国家自然科学基金资助项目(61370089);安徽省自然科学基金资助项目(1208085MA14);安徽省高校省级自然科学研究资助项目(KJ2013Z276);安徽省高等学校省级优秀青年人才基金资助项目(2012SQRL156)和滁州学院校级科研资助项目(2011kj00B)

作者简介：张付丽(1986-),女,安徽临泉人,合肥工业大学硕士生;

doi:10.3969/j.issn.1003-5060.2015.01.029

中图分类号:TN911.22 文献标识码：A

ConstacycliccodesovertheringF2m+uF2mandtheirGrayimages

ZHANGFu-li1,KAI Xiao-shan1,CHEN An-shun2

(1.SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009,China; 2.SchoolofMathematicalSciences,ChuzhouUniversity,Chuzhou239000,China)

Abstract:The relationship between cyclic codes and (1+u)-constacyclic codes over the ring F2m+uF2m is studied, where u2=0.. Further, it is proved that cyclic self-dual codes of any odd length over F2m+uF2m are Type I codes.

Keywords:(1+u)-constacycliccode;cycliccode;Graymap;self-dualcode;TypeIcode

0引言

1预备知识

设环R=F2m+uF2m,其中u2=0,显然环R是一个特征为2的有限交换链环,其极大理想为〈u〉。R上长为n的码C是Rn的一个非空子集,若C为Rn的一个R-子模,则称C为R上长为n的线性码。对Rn中任意的2个码字x=(x0,x1,…,xn-1)、y=(y0,y1,…,yn-1),定义其内积为:

若x·y=0,则称x和y正交。定义线性码C的对偶码为C⊥={x∈Rn|x·y=0,∀y∈C}。若C=C⊥,则称为R上长为n的自对偶码。设c=(c0,c1,…,cn-1)为Rn上的任意码字,Rn上的循环移位σ和(1+u)-常循环移位ν分别定义为:

2Gray映射

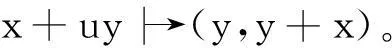
自然地,可以将φ扩展到Rn上,即

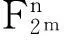
为了利用Gray映射研究R上的线性码,首先给出2个引理。

证明对于任意a(x),b(x)∈R[x],a(x)≡b(x)mod(xn-1)当且仅当存在h(x)∈R[x],使得a(x)-b(x)=h(x)(xn-1),当且仅当a((1+u)x)-b((1+u)x)=h((1+u)x)(((1+u)x)n-1)。而

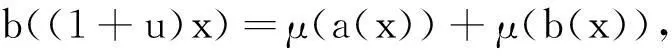
由引理1容易得到推论1。

引理2环R上长为n的线性码C是循环自对偶码当且仅当μ(C)是R上长为n的(1+u)-常循环自对偶码,且每个码字的Lee重量与Gray重量均保持不变。

证明对C中任意的码字c=(c0,c1,…,cn-1),注意到μ(C)=(c0,(1+u)c1,c2,(1+u)c3,…,(1+u)cn-2,cn-1)。

任取C中2个码字a=(a0,a1,…,an-1),b=(b0,b1,…,bn-1),若C是R上长为n的循环自对偶码,则a·b=0,即a0b0+a1b1+…+an-1bn-1=0,由此得到：

从而μ(a)·μ(b)=0。由引理1可知,μ(C)是(1+u)-常循环自对偶码。反之,若μ(C)是R上长为n的(1+u)-常循环自对偶码,则由μ(a)·μ(b)=0类似可得a·b=0。因此,C是R上长为n的循环自对偶码当且仅当μ(C)是R上长为n的(1+u)-常循环自对偶码。最后,欲证每个码字的Lee重量保持不变,只需证明对每个奇数i=1,3,…,n-2,wL(ci)=wL((1+u)ci)。设ci=ai+ubi,其中ai,bi∈F2m。注意到：

从而wL((1+u)ci)=wL(ai+bi,bi)=wL(ci)。同理可证wG(ci)=wG((1+u)ci),由此可得每个码字的Gray重量保持不变。证毕。

3(1+u)-常循环码的Gray像

下面研究R上长为n的(1+u)-常循环码的Gray像,一方面,建立R上(1+u)-常循环码与F2m上循环码之间的联系;另一方面,利用R上(1+u)-常循环码得到F2m上的最优码。

证明由Gray映射的定义,对任意x,y∈Rn,有dG(x,y)=wG(x-y)=wH(φ(x-y))。因φ是同态映射,故wH(φ(x-y))=wH(φ(x)-φ(y))。因此有：

引理4若C是R上长为n的线性码,则φ(C)是F2m上长为2n的线性码。

证明对任意的c,c′∈C,α∈F2m,由于Gray映射φ是加法同态映射,因此有:

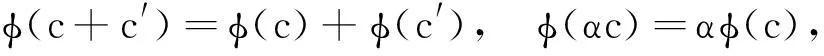
从而φ(C)是线性的。

引理5设σ和ν分别是Rn上的循环移位和(1+u)-常循环移位,则φν=σφ。

证明对任意的c=(c0,c1,…,cn-1)∈Rn,其中ci=ai+ubi,ai,bi∈F2m,0≤i≤n-1。由φ的定义可得:

另一方面,ν(c)=((1+u)cn-1,c0,…,cn-2),而(1+u)cn-1=an-1+u(bn-1+an-1),由此得到:

因此,φν=σφ。

定理1R上长为n的(1+u)-常循环码的Gray像是F2m上长为2n的线性循环码,且dG(C)=dH(C)。

证明设C是R上的线性(1+u)-常循环码,则ν(C)=C,φν(C)=φ(C)。由引理5得σφ(C)=φν(C)=φ(C),所以φ(C)是F2m上长为2n的线性循环码。再由引理3可知,dG(C)=dH(C)。

例1已知F8={0,1,ω,…,ω6},其中ω3+ω+1=0。考虑F8+uF8上长n=9的(1+u)-常循环码。在F8+uF8中有：

其中,f1(x)=x-1；f2(x)=x2+x+1；f3(x)=x2+ωx+1；f4(x)=x2+ω2x+1；f5(x)=x2+ω4x+1。

由引理1可得:

其中,g1(x)=x-(1+u)；g2(x)=x2+(1+u)x+1；g3(x)=x2+(ω+uω)x+1；g4(x)=x2+(ω2+ω2u)x+1；g5(x)=x2+(ω4+ω4u)x+1。

设C是F8+uF8上长为9的(1+u)-常循环码,利用MAGAMA程序可得到φ(C)是F8上[18,14,4]-循环码,该码是一个最优码，即

4F2m+uF2m上的循环自对偶码

文献[5]引入R上类型Ⅰ与Ⅱ码,给出这2类码的许多性质。下面首先给出R上类型Ⅰ与Ⅱ码的定义,然后证明R上长为n的循环自对偶码都是类型Ⅰ码。设C是R上长为n的自对偶码,若C中每个码字Lee重量都是4的倍数,则称C为R上的类型Ⅱ码,否则称C为R上的类型Ⅰ码。

引理6线性码C是R上长为n的自对偶码当且仅当φ(C)是F2m上长为2n的自对偶码。

xx′+xy′+x′y=0,

从而φ(C)⊆φ(C)⊥。因为φ是双射,所以|φ(C)|=|C|。而C是自对偶码,则可推知|φ(C)⊥|=|φ(C)|=2mn,故φ(C)是F2m上长为2n的自对偶码。

定理2线性码C是R上的类型Ⅰ码当且仅当φ(C)是F2m上的类型Ⅰ码。

证明设z=(z0,z1,…,zn-1)∈C,其中，zi=xi+uyi；xiyi∈F2m；0≤i≤n-1,则

于是

已知F2m上循环自对偶码是类型Ⅰ码[10],由此可以得出定理3。

定理3环R上长为n的循环自对偶码是类型码Ⅰ。

证明设C是R上长为n的循环自对偶码,由引理2知,μ(C)是R上长为n的(1+u)-常循环自对偶码,且Lee重量保持不变。由定理1与引理6知,φ(μ(C))是F2m上长为2n的循环自对偶码。已知φ(μ(C))是类型Ⅰ码,由定理2可推出,μ(C)是R上的类型Ⅰ码。由此得到,C是R上的类型Ⅰ码。证毕。

5结束语

[参考文献]

[1]BonnecazeA,UdayaP.Cycliccodesandself-dualcodesoverF2+uF2[J].IEEETransInformTheory,1999,45 (4):1250-1255.

[2]余海峰,朱士信.环F2+uF2上线性码及其对偶码的二元像[J].电子与信息学报,2006,28(11):2121-2123.

[3]李平,朱士信.环F2+uF2上长为2e的循环码[J]. 电子信息学报,2007,29(5):1124-1126.

[4]QianJF,ZhangLN,ZhuSX. (1+u)-constacyclicandcycliccodesoverF2+uF2[J].AppliedMathematicsLetters,2006,19 (8): 820-823.

[5]BestsumiyaK,LingS,NemenzoFR.TypeIIcodesoverF2m+uF2m[J].DiscreteMathematics,2004,273:43-65.

[6]张元婷.环F2+uF2+vF2上的一类常循环码[J].合肥工业大学学报:自然科学版,2013,36(3):381-384.

[7]唐刚,许小芳.环Fp+uFp+vFp循环码[J].武汉大学学报:理学版,2012,58(2):105-108.

[8]ZhuSX,WangLQ.AclassofconstacycliccodesoverFp+vFpanditsGrayimage[J].DiscreteMathematics,2011,311:2677-2682.

[9]KaiXS,ZhuSX,WangLQ.AfamilyofconstacycliccodesoverF2+uF2+vF2+uvF2[J].JSystSciComplex,2012,25:1032-1040.

[10]KaiXS,ZhuSX.Oncyclicself-dualcodes[J].ApplicableAlgebrainEngineering,CommunicationandComputing,2008,19:509-525.

(责任编辑张镅)