无急回运动特性的曲柄摇杆机构的设计
2015-12-31齐晓霞
齐晓霞
(湄洲湾职业技术学院 机械工程系,福建 莆田 351254)
0 引言
曲柄摇杆机构是铰链四杆机构的基本类型之一,在工程中具有广泛的应用前景。急回特性是铰链四杆机构的一个重要特性,可以缩短非生产时间,提高生产率。但是随着机械行业的发展,出现了许多在去程和回程都是工作行程的设备,如空调的摆风机构、电风扇的摇头机构、有株距要求的播种机机构等。因此,对无急回特性的曲柄摇杆机构的研究也变得非常有意义和有价值。
1 曲柄摇杆机构无急回运动特性的条件
连杆机构有无急回运动特性,完全取决于极位夹角θ。当极位夹角θ=0°时,行程速度变化系数K=1,机构没有急回运动特性。
在曲柄摇杆机构ABCD中,设曲柄AB为主动件,BC为连架杆,摇杆CD为从动件,AD为机架;各杆件的长度分别为AB=a、BC=b、CD=c、AD=d,摇杆CD的摆角为φ。机构无急回特性时,极位夹角θ=0°,即CD处于两极限位置时,AB1C1和AB2C2共线,如图1所示。

图1 θ=0°时的曲柄摇杆机构的极限位置
由图1中的几何关系可知:

作DE⊥C1C2,则有:
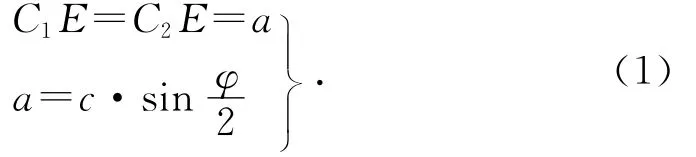
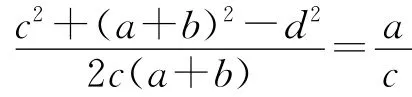

由式(1)、式(2)可知,无急回运动特性的曲柄摇杆机构存在的条件是:①连杆和摇杆的平方和等于曲柄和机架的平方和;②曲柄的长度a等于摇杆长度c和1/2摆角即φ/2的乘积;③最短杆与最长杆的长度和小于等于其余两杆的长度和。
2 无急回运动特性的曲柄摇杆机构的特点
无急回运动特性的曲柄摇杆机构的特点如下:(1)曲柄摇杆机构在某一瞬间会出现铰链中心A、B、C、D位于同一个圆上的情况,如图2所示。

图2 机构四杆长度间的关系
(2)当摇杆处于两个极限位置时,A、B1、B2、C1、C2共线。
3 用图解法设计无急回特性的曲柄摇杆机构
在给定行程速比系数K=1,摆角φ和任意两杆长度时,设计平面曲柄摇杆机构的实质就是确定铰链中心A的位置。
3.1 已知摆角φ、曲柄长度a和摇杆长度c的设计
首先根据给定尺寸大小确定作图比例μ1。如图3所示,任选固定铰链中心D的位置,由摇杆长度c和摆角φ作出摇杆的两个极限位置C1D和C2D。延长连线C2C1并在其上任选一点A作为铰链中心,以A为圆心,a为半径画圆,与C2C1的交点即为铰链中心B的两个极限位置B1、B2。连接AD两点即得机构杆长为:b=μ1×AB1,d=μ1×AD。
由于铰链中心A是任意选的,只要在C1C2连线上即可,故有无穷多解,必须给出辅助条件,才能得出确定的解。
3.2 已知摆角φ、连杆长度b和摇杆长度c的设计
如图4所示,连接C2C1并作其垂直平分线得交点E,由式(1)可知曲柄长度a=C1E,μ1=C2E,μ1。以C1为圆心,(b-a)/μ1为半径画弧,与C2C1的交点即为铰链中心A的位置。连接AD即得机架长度d。
3.3 已知摆角φ、曲柄长度a和连杆长度b的设计
如图 5 所 示,作C1C2=2a/μ1,过C1C2作∠C1C2D=∠C2C1D=90°-φ/2,交点即为铰链中心D的位置。以C1为圆心,(b-a)/μ1为半径画弧,与C2C1的交点即为铰链中心A的位置。连接AD即得机构各构件长度。
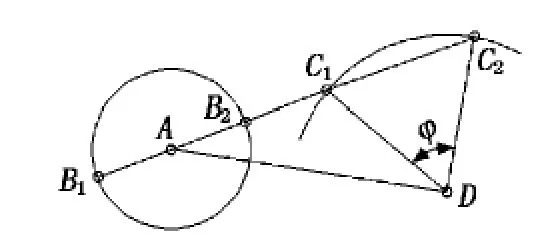
图3 已知摆角φ、曲柄长度a和摇杆长度c的设计简图

图4 已知摆角φ、连杆长度b和摇杆长度c的设计简图

图5 已知摆角φ、曲柄长度a和连杆长度b的设计简图
4 结论
按照给定摆角φ和任意两杆长度,依据无急回特性曲柄摇杆机构的特性就可以确定其余各杆的长度,这种方法使得设计的曲柄摇杆机构具有合理的结构尺寸,而且使设计过程更加简单、灵活。
[1]马璇,马英,高英敏.无急回特性的曲柄摇杆机构的性质及设计[J].机械科学与技术,2003(22):152-153.
[2]方世杰.无急回特性曲柄摇杆机构设计[J].机械设计,2001(4):33-34.
[3]苏有良.无急回特性曲柄摇杆机构新的解析设计法[J].轻工机械,2007(7):60-62.
[4]刘远伟,常勇.无急回运动平面曲柄摇杆机构的图解设计法[J].轻工机械,2006,24(3):53-54.
