基于MATLAB的圆锥滚子圆柱分度凸轮的设计

李建功，王晓月

（河北联合大学 机械工程学院，河北 唐山 063009）

0 引言

圆柱分度凸轮机构中滚子的形式分为圆锥滚子和圆柱滚子。圆柱滚子圆柱分度凸轮磨损较快，调整滚子与凸轮工作面之间啮合间隙也比较困难，因此圆锥滚子凸轮机构比圆柱滚子凸轮机构有更显著的优越性。但圆柱分度凸轮的廓面设计多采用包络法，需要具备包络面理论的知识基础，对此方法的推广和应用带来了一定的困难。本文针对具有圆锥型滚子的分度盘，提出了一种计算凸脊型圆柱分度凸轮轮廓曲面三维坐标的新方法，并在MATLAB中以图形方式绘制出来，根据绘制的曲面对所设计的凸轮进行合理性分析，进而确定凸轮机构的基本尺寸和参数。

1 凸轮的廓面方程

图1为凸脊型圆柱分度凸轮机构示意图。凸轮以角速度ω1匀速转动，推动分度盘做间歇运动。将通过转盘轴线并与凸轮轴线相垂直的平面记为W，以凸轮轴线与W面的交点为原点，以凸轮轴线为z轴建立坐标系oxyz。图1中，Ψ02为分度盘静止时滚子2的初位角，rp为滚子中心到分度盘中心的距离，即分度盘半径，B为滚子宽度，C为分度盘轴线到xoz面的垂直距离，A为凸轮轴线到滚子大端端面的垂直距离。

凸脊型圆柱分度凸轮轮廓展开图如图2所示，其动程段廓面由四部分组成，从上至下依次表示为廓面Ⅰ、廓面Ⅱ、廓面Ⅲ和廓面Ⅳ。下面以廓面Ⅲ为例，说明各廓面方程的建立过程。

按选定的运动规律，建立以凸轮转角δ为参变量的分度盘角位移方程Ψ＝Ψ（δ）和类角速度方程dΨ/dδ＝Ψ′（δ），利用“反转法”求解。如图3所示，保持凸轮静止不动，分度盘与机架以角速度－ω1绕z轴反转，同时分度盘按Ψ＝Ψ（δ）规律相对机架转动。在反转过程中，滚子轴线的运动轨迹即为凸轮的理论廓面。

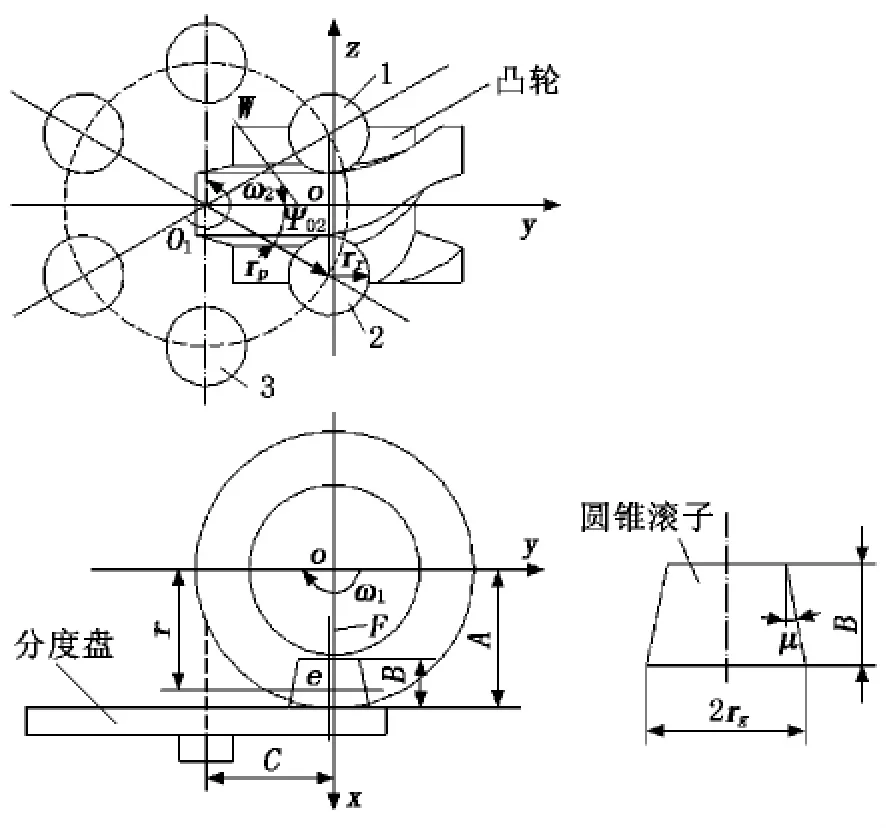
图1 凸脊型圆柱分度凸轮机构示意图

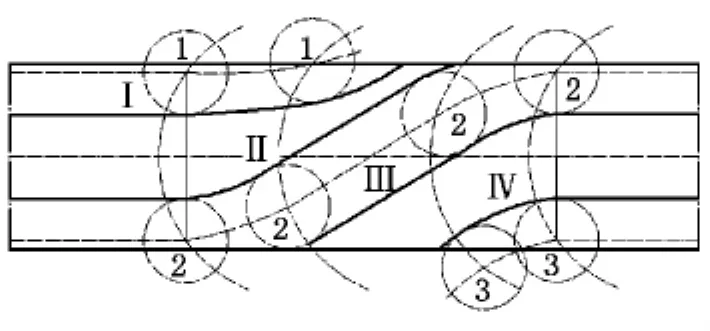
图2 凸脊型圆柱分度凸轮轮廓展开图

图3中，F为与xoz面重合并与分度盘固定且一起反转的平面，e为滚子轴线上的任意点，H－H为过e点的滚子端面。当反转过δ角时，分度盘产生角位移Ψ。

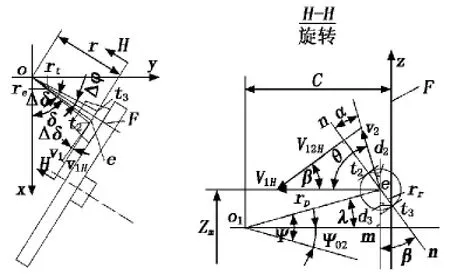
图3 圆柱分度凸轮机构剖视图

由图3所示几何关系可得e点的柱面坐标为：

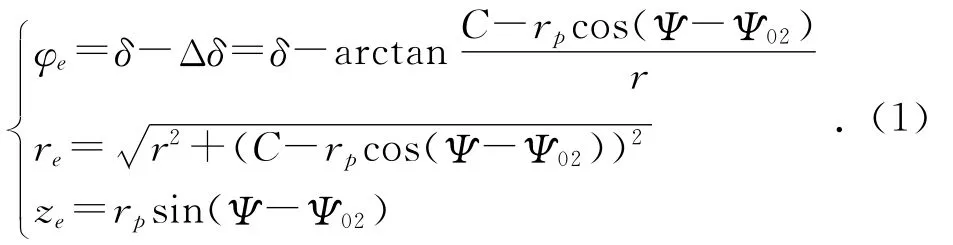
其中：r为H－H面到z轴的距离；Δδ为e点的向径re与F面之间的夹角。由图3可得：

显然，凸轮上e点的速度v1垂直于re，则v1＝reω1。转盘上e点的速度v2垂直于分度盘半径rp，分度盘的角速度为ω2，则v2＝rpω2＝rpdΨ/dt＝rp（dΨ/dδ）（dδ/dt）＝rpω1dΨ/dδ。如图3所示，v1H为v1在H－H面内的分速度，显然有：

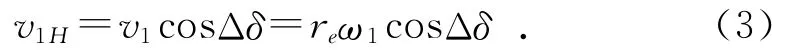
在图3中，θ为v1H与v2之间的夹角，有：

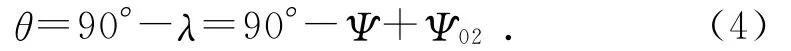
由H－H面内的速度三角形得该面内凸轮与分度盘在e点处的相对速度为：

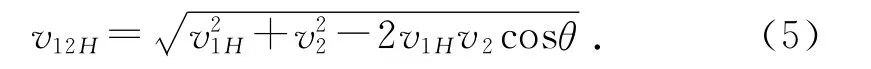
图3中β为v12H与v1H之间的夹角，由正弦定理得：

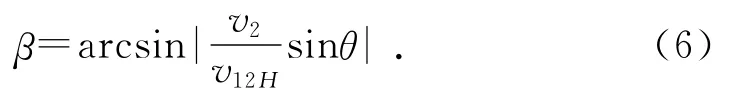
将v2＝rpω1dΨ/dδ和式（3）、式（4）、式（5）代入式（6）并整理得：

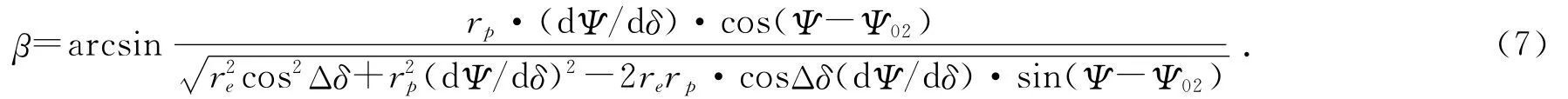
图3中，t3为H－H面内过凸轮廓面Ⅲ与滚子2的接触点，n－n为该面内廓面Ⅲ与滚子2的公法线，rr为该面内的滚子半径，rg为圆锥滚子大端半径，μ为滚子锥角，结合图1可得：

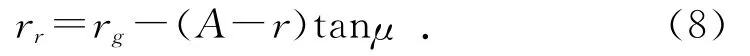
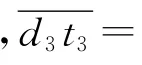
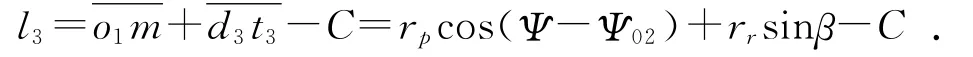
而图3中：

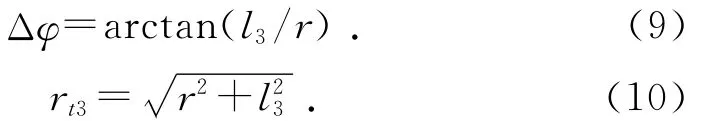
由上述各式整理得t3点的柱面坐标为：

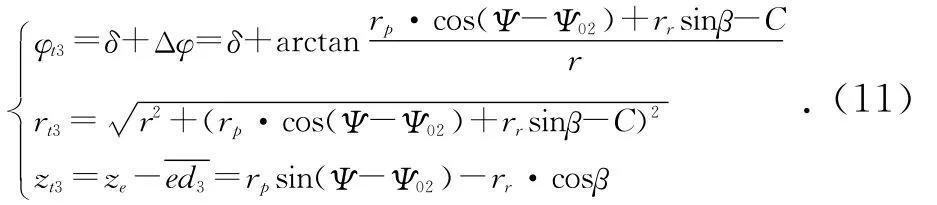
式（11）即为以δ和r为参变量的凸轮廓面Ⅲ的柱面坐标方程。

t2为廓面Ⅱ与滚子2的接触点，t2与t3位置关系如图3所示，廓面Ⅱ和廓面Ⅲ的方程基本相同，按照与上述相同的方法可得t2点的柱面坐标为：

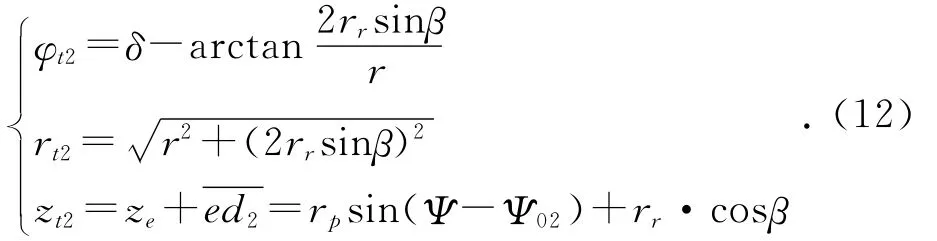
由图2可见，廓面Ⅰ为滚子1的共轭曲面，其廓面方程与廓面Ⅲ的方程基本相同，差别仅在于滚子1的位置角Ψ01＝－Ψ02。廓面Ⅳ为滚子3的共轭曲面，其廓面方程与廓面Ⅱ的方程基本相同，差别仅在于滚子3的位置角Ψ03＝Ψ02＋Ψm。

2 凸轮轮廓曲面的计算与绘制

选定凸轮机构的主要参数如下：C＝90mm；A＝92mm；B＝14mm；rp＝100mm；rg＝14mm；μ＝π/24；动程角δ0＝2π/3；分度盘滚子数z＝12；Ψm＝2π/z＝π/6；选余弦加速度运动规律为凸轮机构的运动规律，即Ψ＝Ψm［1－cos（πδ/δ0）］/2。

根据已推导的方程和给定的参数，利用MATLAB语言编制程序，得到圆柱分度凸轮轮廓曲面，如图4所示。

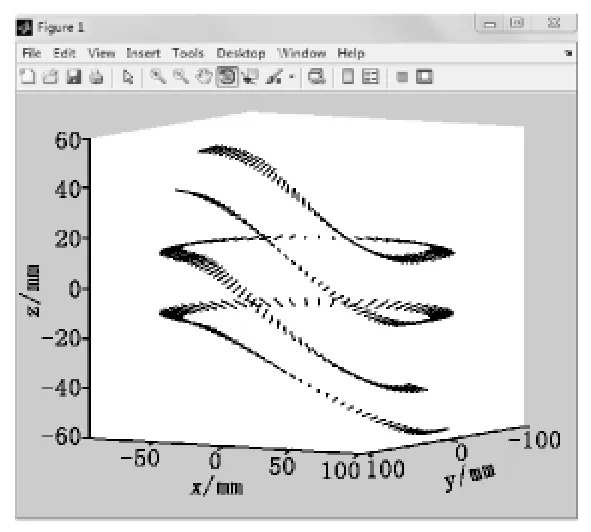
图4 圆柱分度凸轮工作轮廓曲面

3 结语

本文提出了一种采用MATLAB实现凸轮设计的方法，推导出圆锥滚子凸脊型圆柱分度凸轮廓面坐标方程，过程简单，容易理解。取式（8）中μ＝0，则本文所述方法也完全适用于具有圆柱滚子的圆柱分度凸轮的设计。此方法实用性强，有利于一般工程人员掌握和应用。

［1］李建功，黄永强.用柱面坐标计算圆柱滚子直动从动件圆柱凸轮的轮廓曲面［J］.机械工程师，1997（6）：23－24.

［2］彭国勋，肖正扬.自动机械的凸轮机构设计［M］.北京：机械工业出版社，1990.

［3］杜明华，李建功.圆柱滚子摆动从动件圆柱端面凸轮的解析设计［J］.机械设计，2002（6）：23－24.

［4］邹慧君，董师予.凸轮机构的现代设计［M］.上海：上海交通大学出版社，1991.

［5］尚锐.圆锥滚子圆柱分度凸轮廓面的通用方程式［J］.辽宁工学院学报，1997，17（2）：5－8.

［6］郭飞，杨绿云.凸轮机构轮廓曲线在 Matlab中的实现［J］.煤矿机械，2010，31（7）：221－222.