～ρ混合序列加权和的完全收敛性及a.s.收敛性

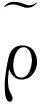
混合序列加权和的完全收敛性及a.s.收敛性

陈晨1，2

(1 中南民族大学 数学与统计学学院，武汉 430074；2 湖北大学 应用数学湖北省重点实验室， 武汉 430062)

摘要在新的条件下讨论了不同分布的混合序列加权和的完全收敛性，获得了混合序列完全收敛的两个充分条件及Marcinkiewicz-Zygmund型的强大数定律.

关键词混合序列；加权和；完全收敛法；a.s.收敛

作者简介陈晨(1980-)，女，硕士，讲师，研究方向：随机级数，E-mail:wenter_198294@163.com

基金项目应用数学湖北省重点实验室开放课题资助项目

中图分类号O211.4文献标识码A

Complete Convergence and Almost Sure Convergence for Weighted

ChenChen1，2

(1 College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074,China;

2 Hubei Key Laboratory of Applied Mathematics, Hubei University, Wuhan 430062,China)

1预备知识与引理

设N为自然数集，{Xn,n≥1}是概率空间(Ω，Ψ，P)上的随机变量序列，Fs=σ(Xi,i∈S⊂N)为σ域，记Lp(Ψ)为所有的Ψ可测且p阶矩有限的随机变量全体，在Ψ中给定σ域F，U，令：

ρ(F,U)=sup{|corr(X,Y)|;X∈L2(F),Y∈L2(U)}.

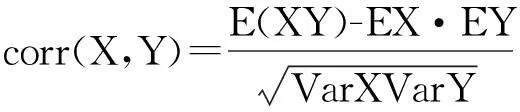
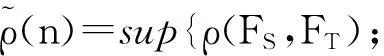
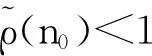
关于独立随机变量的一些经典的极限理论，在20世纪30年代已获得较为完善的发展.实际上我们所遇到的很多问题中的随机变量都是不独立的，因此随机变量的相依性概念引起许多学者的研究兴趣.对于混合序列的情形，已有许多学者给出了一系列深刻的结果，当然这些结果大都是建立在强平稳或者同分布的条件之下.

2完全收敛性

首先我们讨论非同分布的混合序列加权和的完全收敛性.

证明令Xni=XiI(|aniXi|≤nα) ,先证:

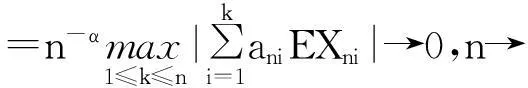
(1)

①当α>1,p≥1时,

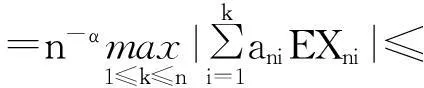
n1-α→0,(n→∞).

②当α>1,p<1时,

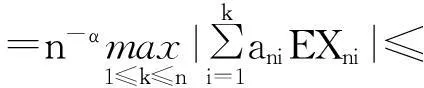
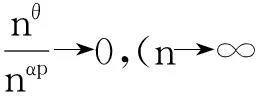
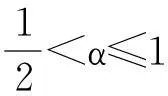
n-αnθn-α(p-1)=nθ-αp→0,(n→∞).

因此∀ε>0,当n充分大时，有

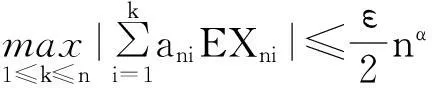
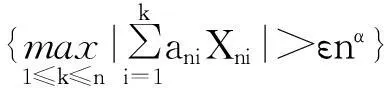
故要证明结论成立，只需证明：

(2)

(3)

先证明(2)式：

在定理1中若θ=1，则有以下相似结论，其证明过程与定理1类似.

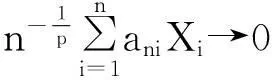
推论1的证明过程与文[3]中定理2的证明方法相同.

3M-Z型强大数定律

证明不失一般性，令|ani|≤n-α,1≤i≤n,n∈N.

Xni=XiI(|Xi|≤nα) ,Yni=XiI(|Xi|>nα) ,

故要证结论成立，只需证：

(4)

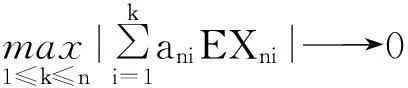
(5)

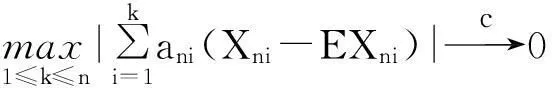
(6)

然后证明(5)式：

最后证明(6)式.由Markov不等式及引理1知，

T1+T2.

故只需证T1,T2<∞.

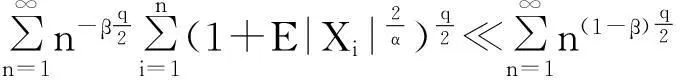
-1,T1<∞的证法同(1).

(3) 当α>1时，取q=2.

由此，定理2得证.

在定理2中若θ=1，则类似地有以下结果.

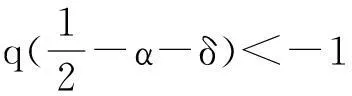
参考文献

[4]Soo Hak Sung. Complete convergence for weighted sums ofρ*-mixing random variables[J]. Discrete Dynamics in Nature and Society, 2010,52:447-454.

[5]Utev S, Peligrad M. Maximal inequalities and an invariance principle for a class of weakly dependent random variables[J].Theoret Probab, 2003(16):101-115.

[6]陈晨.随机级数的T-可和性与本性收敛[J].中南民族大学学报：自然科学版，2013，32(1)：116-119.