一类具时滞的病毒模型的稳定性与Hopf分支

一类具时滞的病毒模型的稳定性与Hopf分支

殷红燕， 宁娣, 周静

(中南民族大学 数学与统计学学院，武汉430074)

摘要研究了一类具有时滞的病毒模型的稳定性和Hopf分支的存在性问题．通过分析特征方程，得到了正平衡点全时滞稳定的充要条件；然后以时滞τ为参数，给出了模型存在Hopf分支的条件和分支值，并对所得理论结果进行了数值模拟.结果表明：时滞τ能够引起系统正平衡点稳定性的改变.

关键词病毒模型；时滞；全时滞稳定性；Hopf分支

收稿日期2014-11-14

作者简介殷红燕(1978-)，女，讲师，硕士，研究方向：微分方程定性理论、分支理论，E-mail: yhy781028@163.com

基金项目中央高校基本科研业务费专项资金资助项目(CZQ13016)

中图分类号O175.13文献标识码A

Stability and Hopf Bifurcation for a Class of Viral Model with Delay

YinHongyan,NingDi,ZhouJing

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

AbstractIn this paper, stability and existence of Hopf bifurcation for a class of viral model with delay are investigated. By analyzing the corresponding characteristic equation, the sufficient and necessary conditions of complete delay stability are obtained. Furthermore, regarding the delay τ as a parameter, conditions of the existence of Hopf bifurcation and bifurcation value are given. Numerical simulations are carried out to illustrate the theoretical results.

Keywordsviral model; delay; complete delay stability; Hopf bifurcation

生物体内存在大量的病毒，同时，也存在着许多抗病毒的细胞. 因此，病毒与抗病毒的相互作用过程成为人们研究的焦点. Bocharov G.A.[1]通过对小鼠分别注射高、中、低剂量的淋巴细胞性脉络丛脑膜炎病毒，观察病毒在小鼠体内的反应，建立了淋巴细胞性脉络丛脑膜炎病毒与抗病毒的细胞毒性T淋巴细胞之间反应的数学模型，并对模型的合理性进行了分析.根据数值分析的方法，给出了模型中各个参数的最优估计和参数的范围.Tatyana Luzyanina[2]通过近些年发展起来的软件包，利用数值分析的方法对Bocharov G.A. 的模型进行了合理简化，得到了如下模型：

(1)

本文研究模型(1)的一种特殊情形：关于特定病毒V的毒害细胞的T淋巴细胞的分裂的持续时间为0，即V(t-τ)中的τ为0.此时模型(1)变为：

(2)

本文对模型(2)进行理论分析，给出该模型全时滞稳定的充要条件，然后以滞量τ为参数, 讨论Hopf分支出现的条件以及分支值，最后,通过数值模拟验证所得理论结果.

1正平衡点的全时滞稳定性

为了讨论模型(2)的正平衡点的全时滞稳定性，首先给出引理1.

引理1[4]具有时滞的常系数线性系统：

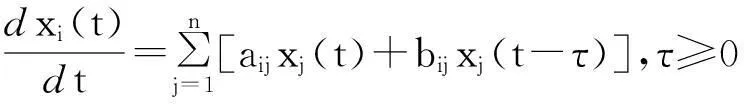
其零解全时滞稳定的充要条件为：

(i) 其特征方程Δ(λ,τ)=0，当τ=0时所有根具有负实部；

(ii) 对∀y,τ∈R，τ>0,均有Δ(iy,τ)≠0.

(3)

令X(t)=x(t)-x0,Y(t)=y(t)-y0,Z(t)=z(t)-z0，则系统(3)变为：

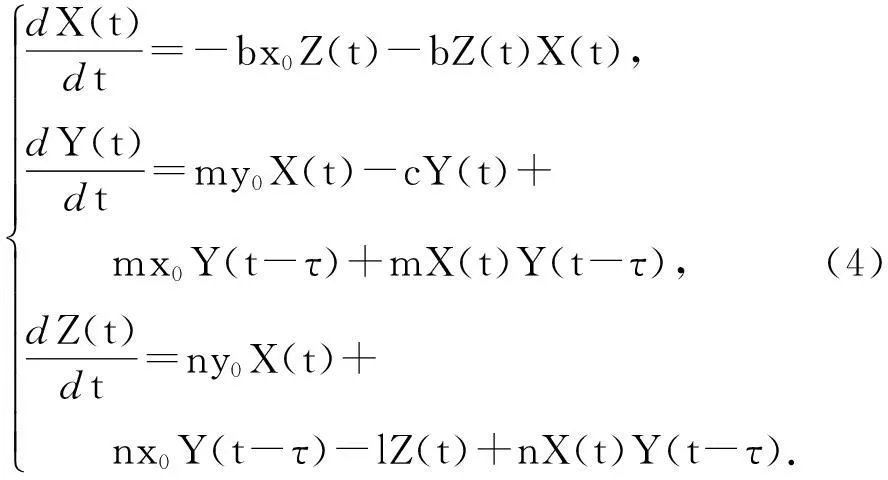
系统(4)的线性近似系统为：

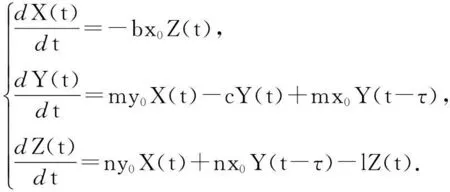
(5)

系统(5)的特征方程为：

λ3+p2λ2+p1λ+p0+(q2λ2+q1λ)e-λτ=0,

(6)

这里p2=l+c,p1=l(c+a),p0=alc,q2=-mx0,q1=-mlx0．

当τ=0，系统(5)变为：

λ3+(p2+q2)λ2+(p1+q1)λ+p0=0.

(7)

由Hurwitz判据，可知方程(6)的两个根均具有负实部的充要条件为：

p2+q2=l+c-mx0>0,

(p2+q2)(p1+q1)-p0=l(l+c-mx0)(c+a-mx0)-alc>0.

当τ>0时，若λ=iω(ω>0)是特征方程(6)的一个根当且仅当ω满足：

(8)

对(8)的两个方程分别平方再相加得：

ω6+h2ω4+h1ω2+h0=0,

(9)

H(σ)=σ3+h2σ2+h1σ+h0=0.

(10)

H(σ)=H1(t)=t3+pt+q,

(11)

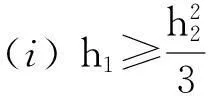
由如上讨论可得系统(3)在平衡点A全时滞稳定的充要条件即定理1.

定理1系统(2)的平衡点全时滞稳定的充要条件是：

(P1) l+c-mx0>0,(l+c-mx0)(c+a-mx0)>ac;

(P2)条件(i)、(ii)、(iii)与(iv)之一成立．

2Hopf分支的存在性

为了讨论Hopf分支的存在性，首先给出如下引理2.

(i) h1<0；

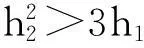
则方程H(σ)=0至少有一个正单根存在.

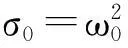
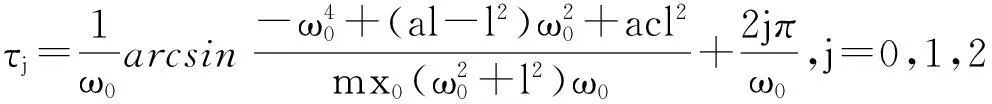
(12)

则λ=±iω0是方程(6)当τ=τj(j=0,1,2,…)时的一对共轭纯虚根，且易证λ=±iω0是唯一的.

对于特征方程(6),两端关于时滞τ求导,整理可得:

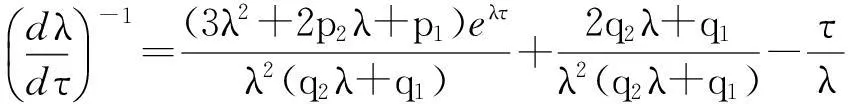
在λ=iω0处，有：

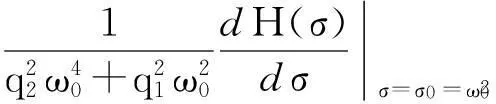
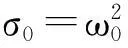
根据引理2和文献[6-8],可得定理2.

定理2如果引理2中的条件成立，则当τ<τ0时，系统(3)的正平衡点A是不稳定的；当τ0<τ<τ1时，系统(3)的正平衡点A是渐近稳定的；当τ=τj(j=0,1,2,…)时，系统(3)在正平衡点A附近产生Hopf分支,其中分支值τ=τj由(12)式确定.

3数值模拟

根据文[1]所给的模型参数的范围，选取a=3.35,b=1.34×10-6,c=0.45,l=0.4,k=265,m=0.001,n=0.01作为系统(3)的一组参数，计算可得τ0≈0.4508.取τ=0.2，所得数值模拟图如图1所示，从而可知，当τ<τ0时，系统(2)的正平衡点是不稳定的；取τ=0.9，所得数值模拟图如图2所示，从而可知，当τ>τ0时，系统(2)的正平衡点是渐近稳定的；当τ=0.444<τ0时，系统存在分支周期解，如图3所示，于是τ0≈0.4508是下临界Hopf分支点.

4结语

本文主要研究了时滞对病毒模型稳定性的影响，以时滞量τ为参数，分析了模型正平衡点的全时滞稳定性和Hopf分支存在的条件. 通过理论分析及数值模拟可以看出：时滞τ能够引起系统正平衡点稳定性的改变.

图1　取τ=0.2<τ 0,系统(2)的正平衡点不稳定 Fig.1　The positive equilibrium of systems (2) is unstable when τ=0.2<τ 0

图2　取τ=0.9>τ 0，系统(2)的正平衡点渐近稳定 Fig.2　The positive equilibrium of systems (2) is asymptotically stable when τ=0.9>τ 0

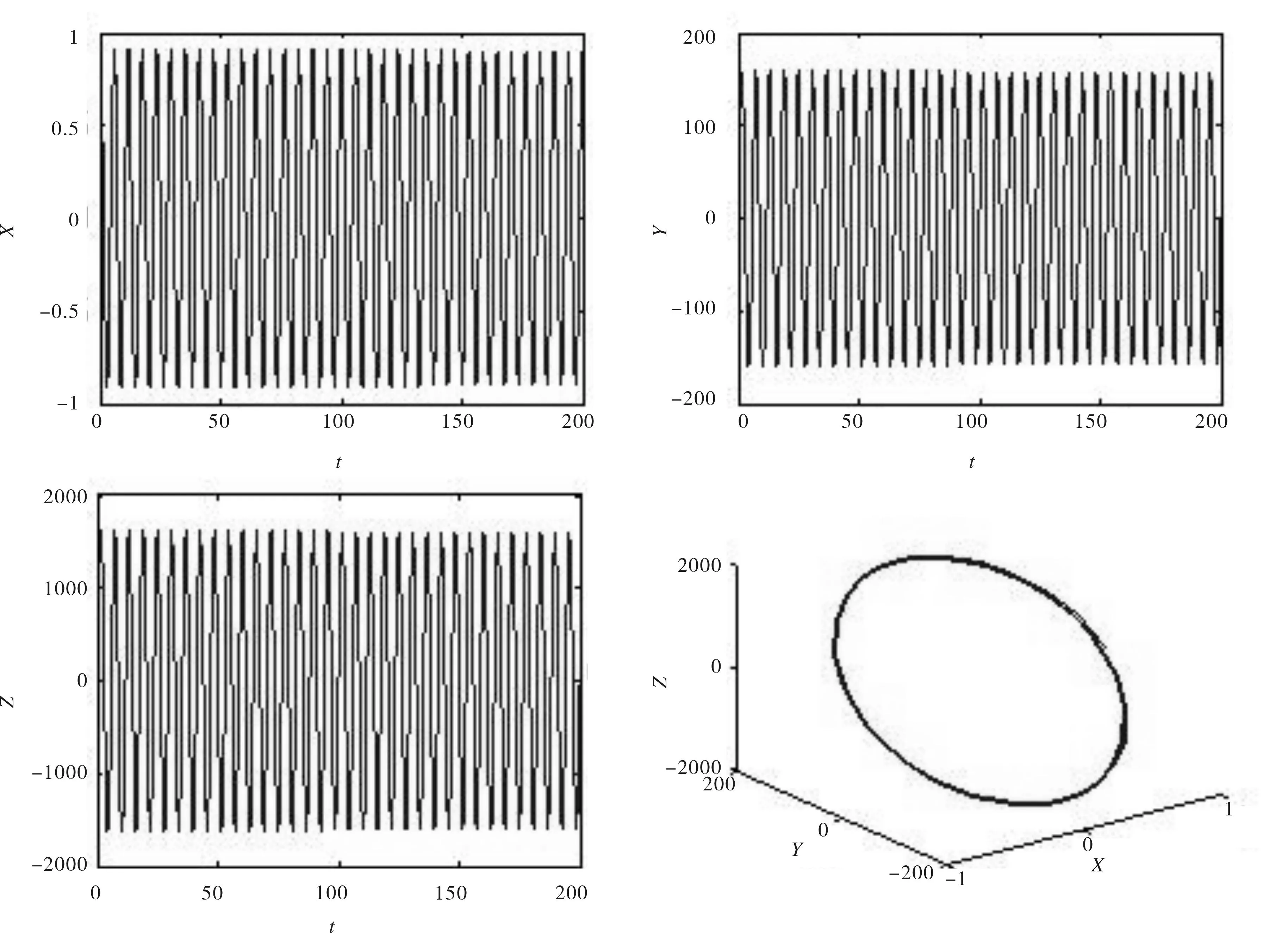
图3　取τ=0.444<τ 0,系统(2)产生周期解 Fig.3　Systems(2) has a period solution when τ=0.444<τ 0

[1]Bocharov G A.Modelling the dynamics of LCMV infection in mice: conventional and exhaustive CTL responses[J]. Journal of Theoretical Biology, 1998, 192(3):283-308.

[2]Tatyana L, Koen E. Low level viral persistence after infection with LCMV: a quantitative insight through numerical analysis[J]. Mathematical Biosciences, 2001,173: 1-23.

[3]徐洪玲.一类具有时滞的病毒模型的Hopf分支[D].长春:东北师范大学数学与统计学学院,2008.

[4]秦元勋，刘永清，王联. 带有时滞的动力系统的运动稳定性[M]. 北京:科学出版社，1963.

[5]黄建科, 陈斯养.一类具时滞的Logistic模型的Hopf分支[J].陕西师范大学学报:自然科学版,2004,32(4):19-22.

[6]刘正荣，李继彬. 哈密顿系统与时滞微分方程的周期解[M]. 北京:科学出版社，1996.

[7]殷红燕.一类具有周期扰动的向日葵方程的次调和分支[J].中南民族大学学报：自然科学版，2012，31(2)：117-119.

[8]殷红燕.向日葵方程的周期扰动Hopf分支[J].中南民族大学学报：自然科学版，2010，29(4)：115-117.