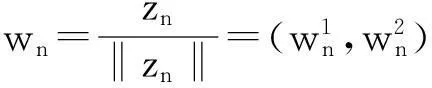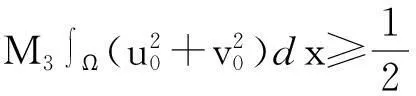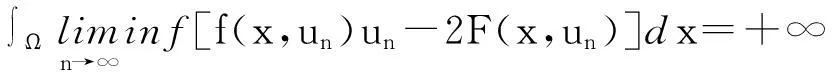带参数的渐近线性椭圆方程组非平凡解的存在性

带参数的渐近线性椭圆方程组非平凡解的存在性

彭超权,刘颖,王芳

(中南民族大学 数学与统计学学院,武汉 430074)

摘要研究了一类带参数的渐近线性椭圆方程组,其非线性项不满足增长性条件.利用山路定理,证明了在一定条件下该方程组非平凡解的存在性.

关键词渐近线性方程组；山路定理；非平凡解

收稿日期2014-10-23

作者简介彭超权(1979-),男,副教授,博士,研究方向：偏微分方程,E-mail: pcq1979@163.com

基金项目中南民族大学研究生创新基金资助项目(2014sycxjj125);中南民族大学中央高校基本科研业务费专项资金资助项目(CZY12013)

中图分类号O175.25文献标识码A

收稿日期2014-10-17

The Existence of Nontrivial Solutions for a Class of

Asymptotically linear Elliptic System with Parameters

PengChaoquan,LiuYing,WangFang

(College of Mathematics and Statistics,South-Central University for Nationalities,Wuhan 430074,China)

AbstractIn this paper,a class of asymptotically linear elliptic system with parameters is studied.The nonlinear term of this elliptic system does not satisfy increasing condition. Under certain conditions, the existence of nontrivial solution to the system is obtained by using Mountain pass theorem.

Keywordsasymptotically linear system; Mountain Pass theorem;nontrivial solution

1问题的引入

本文考虑如下一类带参数的半线性椭圆型方程组

(1)

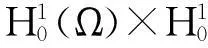
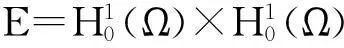
∫Ωf(x,u)φdx-∫Ωg(x,v)ψdx.

与方程组(1)对应的能量泛函为:

I(u,v)=

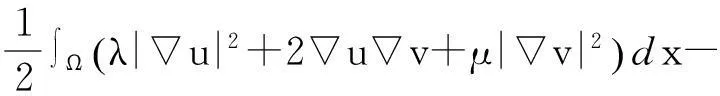
∫ΩF(x,u)dx-∫ΩG(x,v)dx,

在过去几十年里,很多学者关注于研究椭圆方程组(1)中f,g为超线性,参数λ=μ=0的情形[1-3],他们在分数维Sobolev空间中讨论相关问题非平凡解的存在性.在文[4]中LiGB和YangJF利用环绕定理讨论了渐近线性方程组：

-Δu+u=g(x,v),-Δv+v=f(x,u),x∈N,

正解的存在性.而文[5]讨论了方程组(1)中λμ>1,f,g渐近线性时的情形.在文[5]中f,g满足如下条件:

(H1) f,g∈C1(Ω×,),f(x,t)=g(x,t)=0若t≤0;

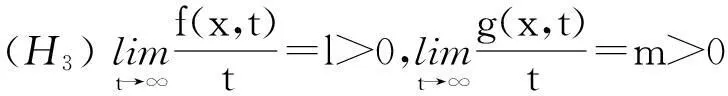
文[5]利用带(PS)条件的山路定理,得到了方程组(1)非平凡解以及最小能量解的存在性.在文[5]中,单调性条件(H4)在验证(PS)序列的有界性时起到了重要的作用.本文拟考虑方程组(1)中λμ>1,f,g为渐近线性但不满足(H4)的情形.为了证明(C)C序列的有界性,我们引入文[6]中提到的条件.

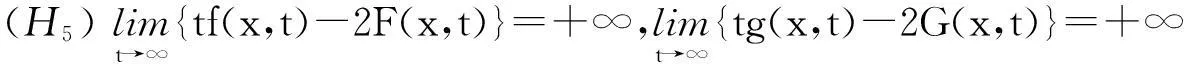
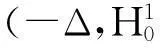
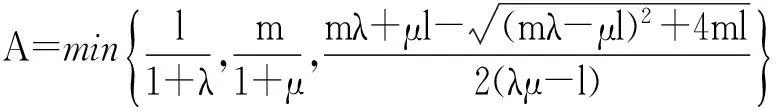
本文的主要结果为定理1.

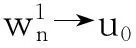
定理1假设条件(H1)～(H3),(H5)成立,如果λ,μ非负,λμ>1且有λ1

2预备知识

因为λ,μ非负且满足λμ>1,由文[5]可知,我们可以在E上定义一个等价范数:

因此,与方程组(1)对应的能量泛函可写为：

I(z)=I(u,v)=

为了证明定理1,我们将用到文[7-9]中提出的山路定理.

引理1设E为Banach空间,I∈C1(E,R)且I满足：

3定理1的证明

引理3[5]假设函数f(x,t)满足条件(H1)～(H3),则有:

(1) ∃ρ,β>0,使得I(z)≥β,‖z‖=ρ;

(2) ∃e∈E,‖e‖≥β使得I(e)<0.

定理1的证明由引理1及引理3可知,存在序列{zn}⊂E满足：

I(zn)→c≥β>0,(1+‖zn‖)I′(zn)→0.

(2)

因为Ω为有界区域,由Sobolev嵌入定理可知,为了得到非平凡解的存在性,只需证明{zn}在E中有界.

我们用反证法来证明.假设当n→∞时有‖zn‖→∞.由式(2)可知,∃M1>0使得:

(3)

其中H(zn)=f(x,un)un-2F(x,un)+g(x,vn)vn-2G(x,vn).

因为I(zn)→c,从而∃M2>0,使得当n充分大时有:

由条件(H1)～(H3)可知,∃M3>0使得F(x,t)≤M3t2,G(x,t)≤M3t2,对∀(x,t)∈Ω×成立,从而有:

(4)

(5)

这与式(3)矛盾,从而定理1得证.

参考文献

[1]Hulshof J,Van De Vorst R C A M.Differential systems with strongly indefinite variational structure[J].J Funct Anal,1993,114:32-58.

[2]Van De Vorst R C A M.Variational identities and applications to differential systems[J].Arch Rational Mech Anal,1991,116:375-398.

[3]De Figueiredo D G, Felmer P L.On superquadratic

elliptic systems[J]. Tras Amer Math Soc,1994,343:99-116.

[4]Li G B,Yang J F. Asymptotically linear elliptic systems [J].Comm PDE,2004,29:925-954.

[5]Peng C Q.Asymptotically linear elliptic systems with parameters[J].Glasgow Math J,2010,52:383-389.

[6]Furtado M F,Maia L A,Silva E A B.On a double resonant problem inRN[J].Diff Int Equations,2002,15:1335-1344.

[7]Zhou H S. An application of a Mountain Pass theorem [J]. Acta Math Scie, 2002, 18(1):27-36.

[8]彭超权.一类渐近线性方程非平凡解的存在性[J].中南民族大学学报：自然科学版，2010，29(4)：118-120.

[9]彭超权，王芳，刘颖.一类半线性椭圆型方程组非平凡解的存在性[J].中南民族大学学报：自然科学版，2014，33(4)：110-112.