一种尺度和方向适应性的Mean Shift跟踪算法

一种尺度和方向适应性的Mean Shift跟踪算法

侯建华1，黄奇1，项俊2,郑桂林1

(1 中南民族大学 智能无线通信湖北省重点实验室，武汉430074；2 华中科技大学 自动化学院，武汉 430074)

摘要针对原始的Mean Shift跟踪算法虽能准确地估计目标位置，但对目标尺度和方向不能实现自适应估计，结合目标模型与候选目标区域的候选模型得到了反向投影图，此反向投影图可表示图像中像素点属于目标的概率，将反向投影图的矩特征应用到原始Mean Shift跟踪算法框架，实现了目标尺度和方向适应性Mean Shift跟踪.实验结果表明：该算法能有效跟踪尺度和方向变化的目标.

关键词mean shift跟踪算法；矩特征；反向投影图；目标跟踪

收稿日期2014-12-19

作者简介侯建华(1964-)，男，教授，博士，研究方向：图像处理、模式识别，E-mail：zil@scuec.edu.cn

基金项目湖北省自然科学基金资助项目(2012FFA113)；武汉市科技供需对接计划项目(201051824575)；中南民族大学中央高校基本科研业务费专项资金资助项目(CZW14057)

中图分类号TP391文献标识码A

Scale and Orientation Adaptive Mean Shift Tracking

HouJianhua1,HuangQi1,XiangJun2，ZhengGuilin1

(1 College of Electronic Information Engineering, South-Central University for Nationalities, Wuhan 430074, China;

2 College of Automation, Huazhong University of Science and Technology, Wuhan 430074, China)

AbstractAlthough the position of target can be well obtained by the original mean shift tracking algorithm, the target’s scale and orientation can not be estimated adaptively. This paper proposed an improved mean shift algorithm to address the issue of how to estimate target’s variation of scale and orientation. Firstly, by combining the target mode and the candidate model, we obtain the weight image which represents the possibility that a pixel belongs to the target. Then the moment features of the weight image are applied in the mean shift tracking framework, so that the scale and orientation changes of the target can be adaptively estimated. The experimental results demonstrate the effectiveness of the proposed algorithm when tracking the target with changes in scale and orientation.

Keywordsmean shift tracking algorithm；moment feature；weight image；object tracking

实时目标跟踪技术是计算机视觉领域的一个热点问题，它是根据先验条件在实时视频帧中寻找目标的位置及形状信息.经过多年的努力，视觉跟踪研究已经取得了长足的进展，涌现出了很多优秀的算法[1].其中基于Mean Shift理论[2]框架的跟踪算法由于具有简单、高效、无参的特点，自提出以来就受到了广泛的关注.经典的Mean Shift跟踪算法[3]利用核函数加权的颜色直方图作为目标模型，用巴氏系数度量模型间相似性，通过Mean Shift迭代寻找目标位置.虽然Comaniciu利用试探法对尺度进行了估计[3],即利用原尺度和变化后的尺度分别进行三次跟踪，选择与目标参考模型相似度最大的尺度作为估计结果，但基于巴氏系数的相似性度量易在较小的尺度中得到局部最优，可能导致实际目标尺度增大时，估计尺度却再逐渐减小.在此基础上，又提出了许多改进的算法[4-7].文献[4]在目标跟踪时，结合Lindeberg等人的尺度空间理论[8]进行实时核函数尺度选择，但是没有对目标方向变化进行估计；Zivkovic等人提出了EM-shift算法[5]，在定位目标位置的同时对目标的大概形状进行描述；Hu等人[6]应用颜色空间特征和相似性测度函数去估计目标的尺度和方向.文献[7]利用非对称核进行Mean Shift迭代，在目标定位、尺度和形状自适应估计方面取得了较好的效果.文献[9]提出了连续自适应Mean Shift算法(Camshift)，该方法应用目标模型计算当前视频帧的反向投影图，并利用反向投影图的矩特征对当前帧目标位置、尺度、方向进行估计, Camshift算法对于序列图像寻优速度快、有较强的实时性与鲁棒性.

已有研究指出，与Camshift中的反向投影图相比较，经典Mean Shift跟踪算法中定义的反向投影图能够更准确的反映目标尺度信息[10].本文对文献[10]的研究进行了理论分析，结合目标模型与候选目标区域的候选模型得到反向投影图，以此估计目标的尺度和方向，实现了一种具有尺度、方向自适应的跟踪算法，并与相关跟踪算法进行了实验对比.

1Mean Shift跟踪算法

1.1目标描述

视频目标跟踪的结果通常被定义为一个矩形或者椭圆区域.目标的颜色直方图对目标的尺度和旋转是相互独立的，并且对局部遮挡具有一定的鲁棒性[3]，因此颜色直方图被广泛应用于目标的表示.

1.1.1目标模型

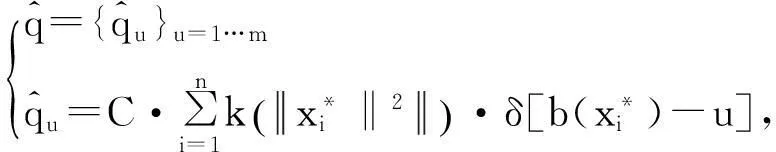
(1)

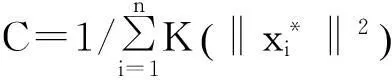
(2)

1.1.2候选目标模型

设y为候选目标区域中心，候选目标模型可以描述为：

(3)

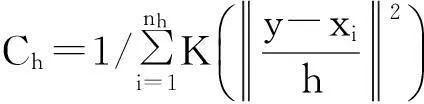
(4)

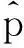
(5)

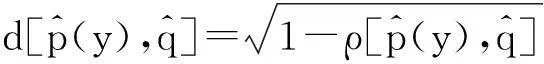
(6)

1.2MeanShift迭代

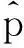
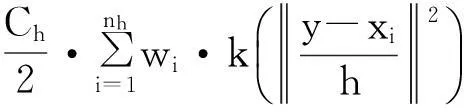
(7)

其中：

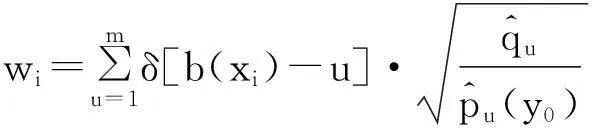
(8)

由于(7)式第一项与y无关，最大化(7)式就相当于最大化(7)式的第二项.经过迭代，目标区域的中心位置由y0移动到新的位置y1，迭代函数为：

(9)

其中g(x)=-k′(x).当核函数轮廓函数k(x)为Epanechnikov，有g(x)=-k(x)=1，所以(9)式可写为：

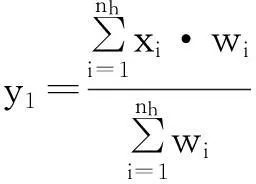
(10)

2尺度、方向适应性Mean Shift

在视频序列中，目标的缩放是一个缓慢的过程.因此，我们可以假设目标的尺度变化是平滑的，这个假设在大部分视频序列是成立的.于是我们可以在原始的Mean Shift跟踪算法[3]的基础上提出改进方案.假设已经估计出前一帧目标区域的面积，我们可将当前帧候选目标区域面积(尺度)定义为比前一帧目标稍大.因此，不管目标的尺度和方向怎样变化(只要帧间变化是缓慢的)，它都不会超出当前帧定义的候选目标区域.此时，估计目标尺度和方向的问题就转化为对候选目标区域面积、以及候选目标方向的确定.

2.1尺度变化时目标的反向投影图

参考文献本文尺度、方向适应性Mean Shift(简称SOAMST)方案[9]，通过计算反向投影图的矩特征[11]来估计目标的尺度和方向.然而这些矩特征仅仅依赖反向投影图，这就要求有一种合理的反向投影图计算方法，进而得到准确的矩特征去有效的估计目标变化.在Camshift[9]和Mean Shift跟踪[3]算法中，都利用了反向投影图[4]来完成目标跟踪.其中，Camshift的反向投影图是由目标区域的色度(Hue)直方图反向投影得到；而Mean Shift跟踪算法的反向投影图是由(8)式定义得到.在此，我们将通过分析Camshift和Mean Shift跟踪算法的反向投影图在不同尺度下的情况，以从中选优提升SOAMST算法.

如前所述，我们定义一个比目标本身尺寸更大的候选目标区域，以确保在跟踪过程中目标总出现在候选目标区域内.在该策略下，可以比较目标在不同尺度下分别用Camshift和Mean Shift跟踪方法所得反向投影图.参考文献[3,9]可得图1.其中，图(m)是一个由三个灰度级组成的合成目标；图(n)为比目标更大的候选区域；图(a)、(b)、(c)分别为合成目标尺度缩小、不变、增大的跟踪结果；图(d)、(e)、(f)分别为对图(a)、(b)、(c)应用Camshift算法计算所得反向投影图；而图(g)、(h)、(i)分别为对图(a)、(b)、(c)应用Mean Shift跟踪算法计算所得反向投影图.

从图1中，可以看到Camshift和Mean Shift跟踪对同一目标计算所得反向投影图的不同.首先，Camshift算法所得反向投影图像素值为常量，并且该常量仅仅与目标模型有关；而Mean Shift跟踪算法所得反向投影图像素值会随目标尺度变化而变化.当目标的尺度与候选目标区域大小越接近，Mean Shift跟踪算法所得反向投影图像素值就越接近常量1.也就是说，Mean Shift跟踪算法所得反向投影图能更好的反映目标尺度的变化.根据以上的观测和分析，我们将采用Mean Shift跟踪算法所用反向投影图计算方法.

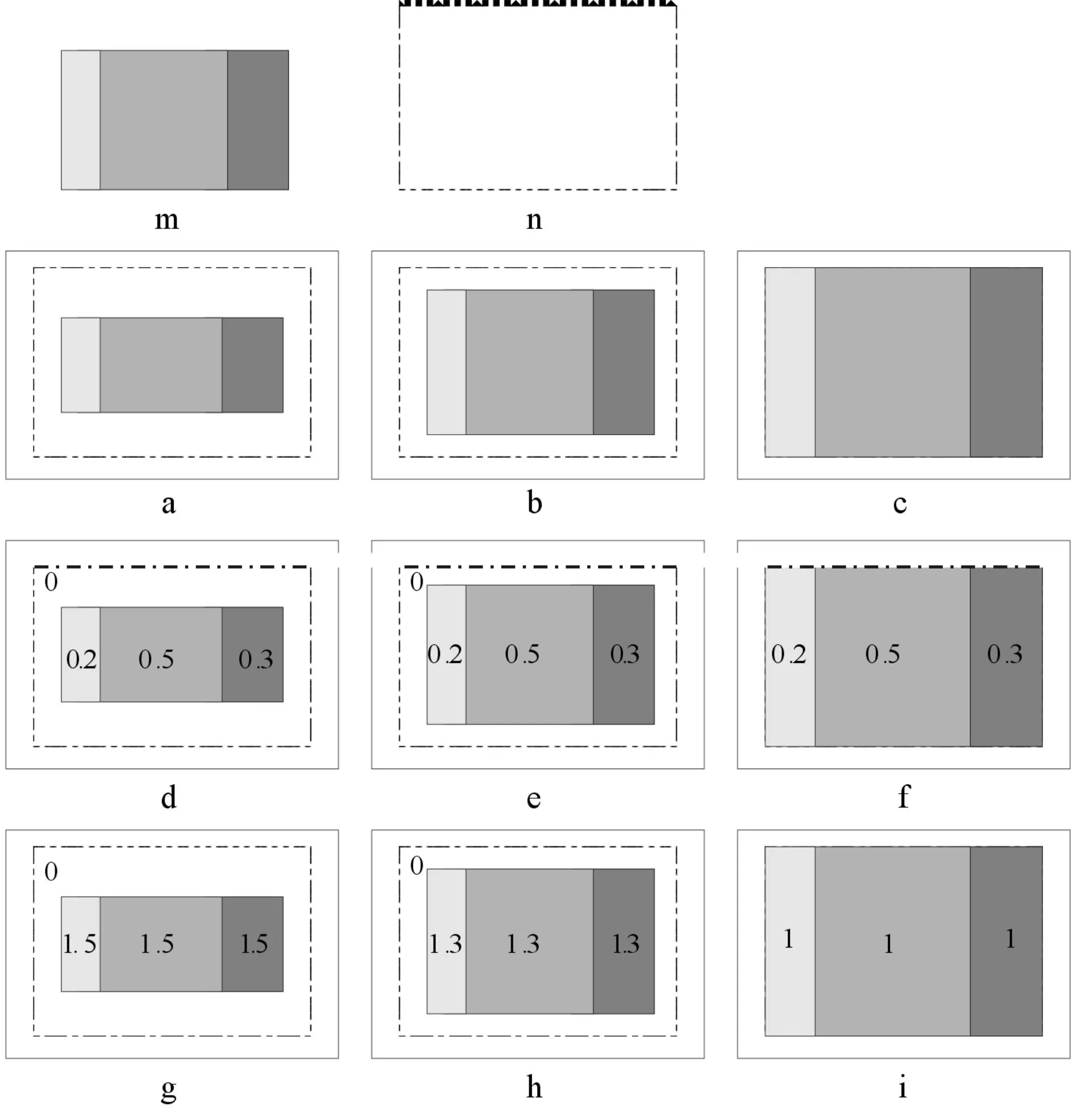
图1　目标在不同尺度下用Camshift和Mean Shift 跟踪算法所得反向投影图 　Fig.1　Weight images in Camshift and Mean Shift tracking algorithms when the object scale changes

2.2目标面积的估计

由于候选目标区域的反向投影图像素值表示像素点属于目标的可能性，所以候选目标区域的权重面积可以表示成反向投影图的零阶矩：

(11)

在MeanShift跟踪中，目标通常会在一个比自己更大的候选目标区域内.由于候选目标区域存在背景特征，所以候选目标区域内目标特征的概率就会比目标模型对应概率要小.(8)式就会增大目标像素的权重，同时会减小背景像素的权重.也即在估计目标面积上，候选目标区域的目标像素比背景像素起更大的作用.这在图1中图(g)、(h)、(i)是清晰可见的.

根据以上分析，可以用巴氏系数来修正M00，以合理估计目标面积A.定义目标面积估计函数：

A=c(ρ)·M00，

(12)

其中c(ρ)是一个关于巴氏系数ρ(0≤ρ≤1)单调递增函数.结合图1中图(g)、(h)、(i)，通常都大于目标面积，并且它随着ρ增大而单调地接近目标真实面积.因此，我们需要c(ρ)是单调递增函数，并且ρ取1时c(ρ)取得最大值1.通过实验，结合指数函数与高斯函数得到的c(ρ)能取得令人满意的结果[10]，c(ρ)定义为：

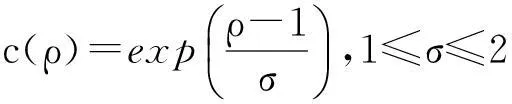
(13)

结合式(12)、(13)，当ρ接近上限1时(目标候选模型接近目标模型)，c(ρ)也接近1，也即M00作为目标面积估计更加可靠.当ρ减小时(目标候选模型与目标模型的差异增大)，M00会大于目标面积，但c(ρ)会小于1，以使得A能合理的表示目标的真实面积.当ρ接近0时，说明目标已经跟丢，A也将接近零值.

2.3矩特征的应用

参考文献[9]，计算反向投影图的一阶矩M10、M01，二阶矩M20、M02、M11：

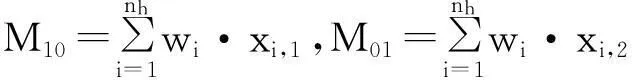
(14)

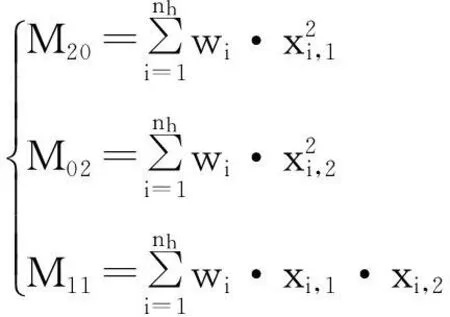
(15)

其中，(xi,1，xi,2)为候选目标区域内像素点的坐标.

比较式(10)、(11)、(14)，可以发现当前帧目标的所在位置y1为一阶矩与零级矩的比：

(16)

参考文献其中代表目标候选区域的中心坐标.[11]，结合式(10)、(11)、(15)和(16)可以定义中间变量μ20、μ11、μ02，并写成协方差矩阵形式：

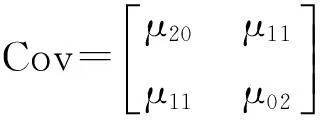
(17)

其中：

(18)

2.4估计目标的宽、高及方向

结合目标的面积估计值及目标的协方差矩阵(17)式，可以得到目标的宽、高及方向估计.对(17)式协方差矩阵进行奇异值分解(SVD)：

Cov=U×S×UT=

(19)

其中：

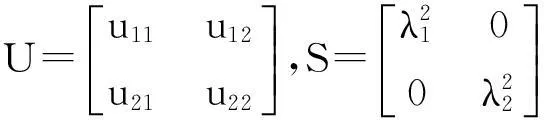
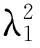
由于利用了反向投影图来近似目标在候选区域的可靠密度分布函数，所以利用U对目标的方向进行估计就会更加可靠.下面将对目标宽和高进行精确的估计.

假设跟踪目标被表示为一个椭圆，椭圆的长半轴、短半轴分别用a、b表示.文献[11]证明，λ1与λ2的比约等于a与b的比，即λ1/λ2≈a/b.因此，可以设a=k·λ1、b=k·λ2，其中k为尺度因子.由于我们已经估计得到目标面积A，又这里A=π·a·b=π·(kλ1)·(kλ2)，所以有：

(20)

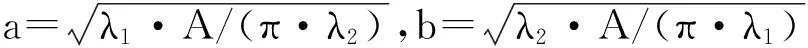
(21)

现在协方差矩阵可以表示为：

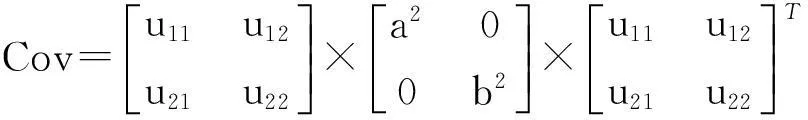
(22)

协方差矩阵Cov重写为(22)式形式是本文算法的关键步骤.值得提及的是Zivkovic等人提出的EM-shift算法[5]，它是根据MeanShift跟踪算法对视频帧进行协方差矩阵的迭代估计.而本文算法是结合目标面积A和协方差矩阵，对目标的宽、高和方向进行估计.

2.5下一帧候选区域的确定

完成了对当前帧目标位置、尺度和方向的估计，接下来就需要确定下一帧目标的候选区域.根据(22)式，我们定义如下协方差矩阵表示下一帧候选目标区域的尺度：

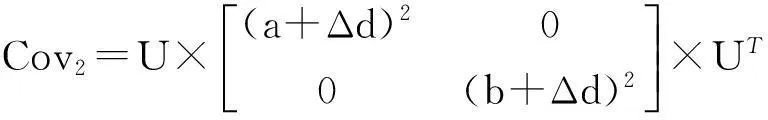
(23)

其中，Δd是下一帧目标候选区域尺度在前一帧基础上的增长量.目标候选区域的位置被初始化为(椭圆区域):

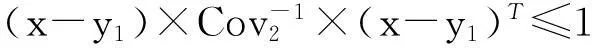
(24)

2.6SOAMST算法实现

根据前面的分析，SOAMST算法的实现步骤如下：

(2)初始化迭代次数变量：k=0.

(4)应用(8)式计算得到权重向量{wi}i=1…n.

(5)应用(10)式计算目标候选模型的新位置y1.

(6)定义d=‖y1-y0‖,y0=y1.并设置误差阈值ε，迭代次数上限N.

if(d<εork≥N：跳到第(7)步执行；

else：k=k+1，跳到第(3)步执行.

(7)应用(22)式估计目标候选模型的宽、高、方向.

(8)应用(24)式估计下一帧目标候选模型.

3实验结果

将SOAMST算法与原始Mean Shift跟踪算法[3]、EM-shift算法[5]进行实验结果对比，对SOAMST算法进行客观评价.Mean Shift跟踪算法与EM-shift算法是在Mean Shift框架下、在处理目标尺度和方向变化领域两个具有代表性的方案.由于Camshift框架得到的反向投影图不够可靠，它在估计目标尺度和方向上容易出现错误，所以没有将Camshift加入到实验对比.

本文采用RGB颜色空间作为特征空间，并且将

颜色空间量化为16×16×16级.我们选择一个对称视频序列和一个场景视频序列作为实验对象.

3.1对称视频序列上的实验

我们首先选用一个对称椭圆视频序列来测试SOAMST算法的准确率.如图2，第1行是Mean Shift跟踪算法实验结果；第2行是EM-shift算法实验结果；第3行是SOAMST算法实验结果.实验结果中，黑色椭圆框表示跟踪得到的目标区域，灰色椭圆框表示SOAMST算法所述的候选目标区域(本实验参数Δd=10).实验结果表明，SOAMST算法能可靠的跟踪尺度及方向同时变化的椭圆.同时，Mean Shift跟踪算法不能估计目标的方向，并且其跟踪结果不佳；EM-shift算法未能较准确的估计对称椭圆的尺度及方向.

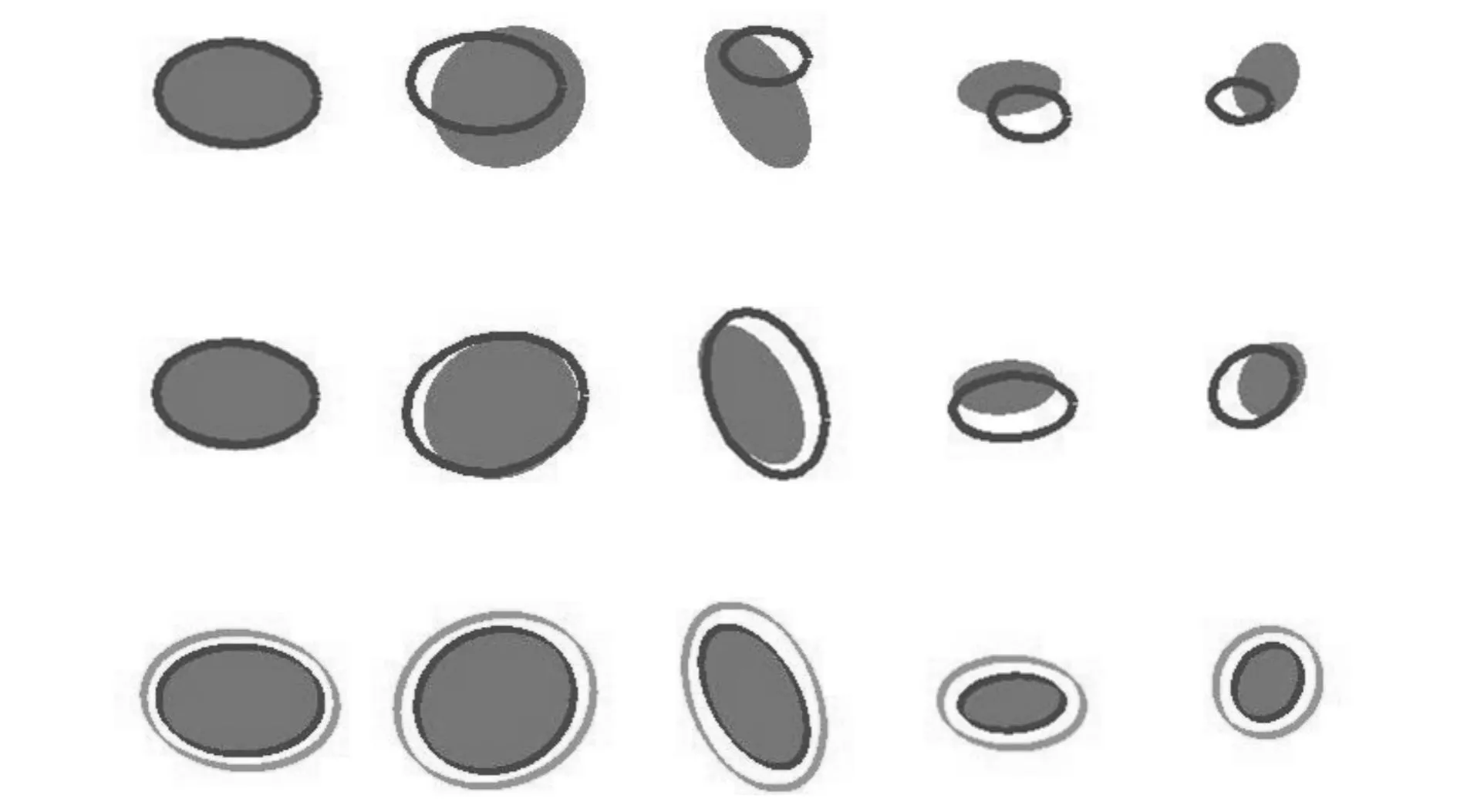
Frame 1 　 Frame 7　　Frame 25　Frame 38　Frame 49 图2　三种跟踪算法在对称椭圆序列上的跟踪结果 Fig.2　Tracking results of the synthetic ellipse sequence by three tracking algorithms

表1列出了SOAMST算法对对称视频序列中椭圆宽、高和方向的估计.其中方向为椭圆的主轴与x轴的角度.序列的第一帧用于定义目标模型，剩下的视频帧用于算法测试.可见，SOAMST方法在估计目标尺度和方向上获得了准确的效果.

表1　SOAMST算法对对称视频序列中椭圆宽、高和方向的估计结果及准确率

3.2场景视频序列上的实验

场景视频序列的目标是一个羽毛球拍手胶，该目标的尺度、方向变化明显.见图3，第1行是Mean Shift跟踪算法的实验结果；第2行是EM-shift算法的实验结果；第3行是SOAMST算法的实验结果.可见，Mean Shift跟踪算法没有获得好的跟踪效果；另一方面，虽然EM-shift算法较Mean Shift跟踪算法获得了更好的跟踪效果，但它在目标方向快速变化时仍不能及时准确的跟踪；而SOAMST算法所得跟踪结果是较准确的.

图3　3种跟踪算法在场景序列上的跟踪结果 Fig.3　Tracking results of the real-time video sequence by three tracking algorithms

表2列出3种方案分别在两个视频序列上跟踪时的平均迭代次数.由于Mean Shift跟踪算法会进行3次Mean Shift迭代，所以它的迭代次数最多.影响EM-shift和SOAMST算法收敛速度的主要因素是协方差矩阵的计算.由于EM-shift每次迭代会进行一次目标位置和方向的估计，而SOAMST每帧只进行一次目标位置和方向的估计，所以SOAMST比EM-shift更快.

表2方案在视频序列上跟踪时的平均迭代次数

Tab.2Average number of iterations by different methods

on the two sequences

算法MeanShiftEM-shiftSOAMST对称椭圆序列29.312.43场景序列28.813.65.08

4结语

在Mean Shift跟踪算法框架下，结合候选目标区域反向投影图的矩特征，实现了一种对目标尺度和方向适应性估计的SOAMST跟踪算法.实验结果也表明，SOAMST算法继承了原始Mean Shift跟踪算法简单、高效等优良特性.在以后的研究工作中，我们可以通过检测目标的真实形状来更加准确的表达目标，而不是单纯的选取椭圆或矩形模型，以进一步提高跟踪的准确性.

参考文献

[1]Yilmaz A, Javed O, Shah M. Object tracking: a survey [J]. ACM Journal of Computing Surveys, 2006, 38(4): 1-45.

[2]Fukunaga F, Hostetler L D. The estimation of the gradient of a density function, with applications in pattern recognition[J]. IEEE Trans Inf Theory, 1975, 21(1):32-40.

[3]Comaniciu D, Ramesh V, Meer P. Kernel-based object tracking[J]. IEEE Trans Pattern Anal Mach Intell, 2003, 25(5):564-577.

[4]Collins R T. Mean-shift blob tracking through scale space[C]//IEEE. Conference on Computer Vision and Pattern Recognition. Wisconsin:IEEE,2003: 234-240.

[5]Zivkovic Z, Krose B. An EM-like algorithm for color-histogram based object tracking[C]//IEEE. Conference on Computer Vision and Pattern Recognition. Washington DC:IEEE, 2004: 798-803.

[6]Hu J, Juan C, Wang J. A spatial-color mean-shift object tracking algorithm with scale and orientation estimation[J]. Pattern Recognit Lett, 2008, 29(16): 2165-2173.

[7]Quast K, Kaup A. Scale and shape adaptive mean shift object tracking in video sequences[C]//ESPC. European Signal Processing Conf. Glasgow:IEEE, 2009: 1513-1517.

[8]Bretzner L, Lindeberg T. Qualitative multi-scale feature hierarchies for object tracking[J] J Vis Commun Image Represent, 2000, 11(2): 115-129.

[9]Bradski G. Computer vision face tracking for use in a perceptual user interface[J]. Intel Technol J, 1998, 2 (2): 1-15.

[10]Ning J, Zhang L, Zhang D, et al. Scale and orientation adaptive mean shift tracking[J]. IET Computer Vision, 2012,6(1): 52-61.

[11]Mukundan R, Ramakrishnan K R. Moment functions in image analysis: theory and applications[M]. Singapore: World Scientific, 1998.