等离子体涂覆复杂目标电磁散射的间接Z变换时域有限差分法
2015-12-31王旭阳钟卫军
卢 雁,王旭阳,钟卫军
(1.中国人民解放军94259部队,山东 蓬莱 265600;2.空军工程大学 导弹学院,陕西 三原 713800)
0 引言
隐身武器在电子战、信息战中扮演重要角色。定量描述目标雷达特征的参量是雷达散射截面(RCS),以降低目标RCS为目的的隐身技术主要包括外形隐身、雷达吸波材料隐身、无源对消和有源对消技术,前两种最常用。随着科技技术的进步,新的隐身机理和新型吸波材料不断涌现,等离子体隐身技术成为研究热点[1-2]。时域有限差分法是一种有效处理复杂介质电磁问题的方法,分析等离子体电磁问题的方法主要有 DE-FDTD,RC-FDTD,ZTFDTD,JEC-FDTD,PLRC-FDTD,PLJERC-FDTD,SO-FDTD 等[3-17]。 其 中:RC-FDTD,JEC-FDTD,PLRC-FDTD,PLJEC-FDTD法在时域求解中会涉及复杂的卷积运算;ADE-FDTD法在推导时域迭代过程中也需要复杂的数学运算;ZT-FDTD法虽无卷积运算,但在从频域到Z域转换过程中会有复杂的数学转换公式;SO-FDTD法无需计算复杂的卷积,迭代过程中不出现复数变量,公式简单,便于编程实现,给出了不同模型统一的迭代方程形式,但没有给出该迭代方程迭代系数的统一形式。基于SOFDTD法的算子变换,在文献[3、5-6、15-17]的基础上,本文对用间接Z变换算子分析等离子体的电磁特性的方法进行了研究。
1 非磁化等离子体的间接Z变换时域有限差分法
非磁化等离子体的Maxwell方程组及辅助方程为
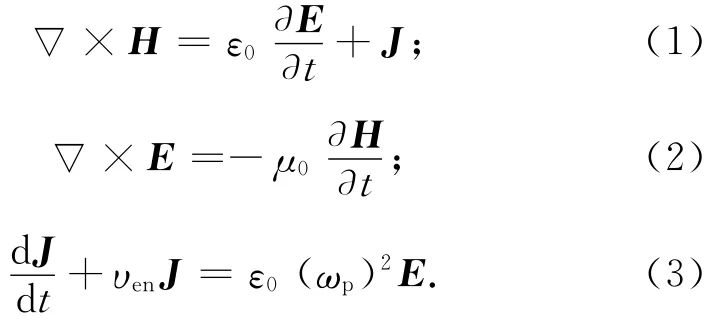
式中:E为电场强度;H为磁场强度;J为电流密度;ε0为自由空间介电常数;μ0为自由空间的磁导率;υen为等离子体碰撞频率;ωp为等离子体角频率。将式(3)转换为频域表达式,可得J,E的本构关系表达式为


电通密度D,E的本构关系可写为

由上述分析可知:可用两种方式得到非磁化等离子体的迭代表达式,一是通过J,E本构关系推导,二是通过D,E本构关系推导。通过J,E本构关系进行迭代运算时,中间变量少,编程简单,故本文用J,E本构关系推导非磁化等离子体的迭代公式。
1.1 间接Z变换算子
文献[2、16]在推导色散介质的FDTD方程时,用直接求取Debye介电模型Z变换方法建立了FDTD的迭代方程,但最后得出的方程较复杂且无统一的规律可循。实际应用中,直接推导出各种不同的介电模型的Z变换公式相当困难,更可行的方式是采用间接方法。
根据傅里叶变换理论,函数y(t)的频域表达式为

式中:Y(ω)为y(t)对应的频域函数,且y(t)的导函数

根据导数的定义,时间导数算子在时域中的离散形式为

进行Z变换
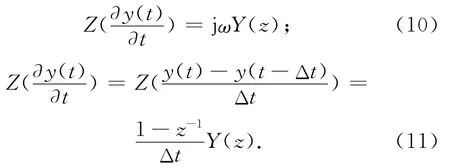
对照式(10)、(11),频域算子和Z变换域的对应关系为


1.2 基于J,E本构关系的ZFDTD方法
取E位于整数时间步,H,J位于半个时间步,并取J的位置与E相同。可得式(1)、(2)的离散表达式分别为


将式(3)写成频域分量形式

由式(20)可知:满足有理分式模型的一阶模型且形式相同,只需分析一个分量即可。将间接Z变换算子引入式(20)中,则

式(21)可简化为
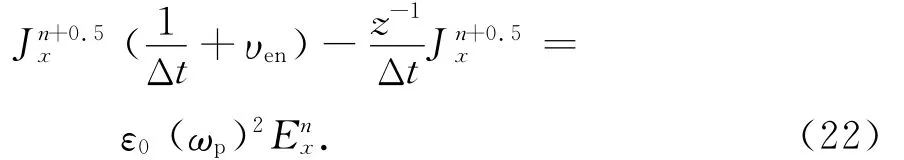
由Z变换原理,式(22)可表示为

同理,可得


综合上述离散时域表达式,根据J,E关系的非磁化等离子体ZFDTD方法编程计算递推过程为:
a)由式(17)~(19)得到E到H的递推计算;
b)由式(23)~(25)得到E到J的递推计算;
c)由式(14)~(16)得到E,J到E的递推计算;
d)按步骤a)、b)、c)的计算顺序进行下一轮的递推计算。
2 数值算例
2.1 算法有效性验证
算例1非磁化等离子体:设非磁化等离子体球半径3.75mm,等离子体电子回旋频率ωb=0,ωp=2π×28.7×109rad/s,υcn=20GHz。计算中取FDTD元胞尺度δ=5×102mm,Δt=δ/(2c);高斯脉冲沿z轴入射,脉冲宽度τ=60Δt,t0=0.8τ。用J,E本构关系的ZFDTD方法计算的非磁化等离子球后向RCS如图1所示。由图可知:本文计算值与文献[17]的Mie级数所得的准确结果吻合,表明本文方法正确。
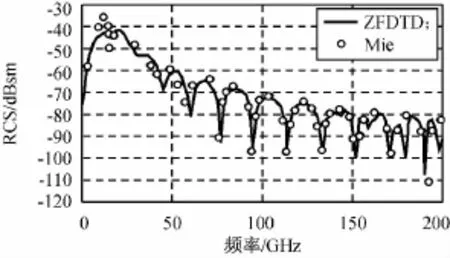
图1 非磁化等离子球的后向RCSFig.1 Backscattering RCS of non-magnetic plasma sphere
算例2导弹1:文献[8]中导弹如图2所示,对导弹模型进行建模,用ZFDTD算法计算该导弹的单站RCS,并与该导弹模型的实测结果和文献[8]的计算结果比较。ZFDTD方法计算中参数设置与文献[1]相同,高斯脉冲由鼻锥方向入射时,导弹单站RCS的ZFDTD计算值(无等离子体涂层)、测量值(无等离子体涂层),文献[8]中等离子体覆盖时单站RCS计算值和等离子体覆盖时单站RCS的ZFDTD计算值如图3所示。图中:d=3表示涂覆的等离子体有3个网格(12mm)。仿真结果表明了ZFDTD方法分析复杂目标电磁散射特性的准确性及分析等离子体覆盖复杂目标电磁散射特性的有效性。

图2 导弹模型Fig.2 Model of type 1missile

图3 高斯脉冲由鼻锥方向入射时导弹模型单站RCSFig.3 Monostatic RCS of missile model when Gauss pulse incidence in nose direction
2.2 复杂目标的电磁散射特性分析
算例3 飞机1:缩比模型如图4所示,包括锥台1个、圆台2个,圆柱1个、两个互成180°的机翼1、两个互成180°的机翼2和尾翼,其中机翼1的h=50mm,d=2mm,l1=30mm,l2=10mm;机翼2的h=80mm,d=2mm,l1=60mm,l2=12mm;尾翼的h=70mm,d=2mm,l1=14mm,l2=45mm。飞机轴线与z轴重合,机头指向z轴正向,y轴正向与其中一个弹翼轴线重合。入射脉冲采用高斯脉冲,计算时间步长Δt=1.58ps,τ=0.133ns,计算频率0.001~15GHz,剖分后x,y,z方向的单元数分别为70,76,148。

图4 飞机1模型Fig.4 Structure of type1plane model
令等离子体碰撞频率为100GHz且保持不变;飞机外壳涂覆等离子体厚度为5mm,在等离子体电子数密度分别为0.6×1018,0.8×1018,1.0×1018m-3条件下飞机的单站RCS计算结果如图5所示。
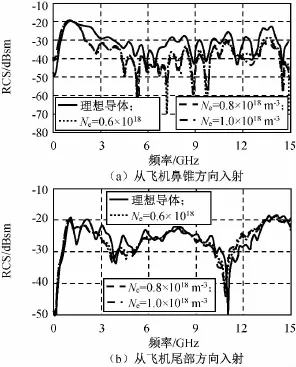
图5 不同等离子体电子数密度下飞机1单站RCSFig.5 Monostatic RCS of plane model under various plasma electron number density
令等离子体电子数密度为0.8×1018m-3且保持不变;导弹外壳涂覆等离子体厚度δ为5mm,在等离子体的υen分别为60,100,500GHz条件下,电磁波沿尾部方向入射时飞机1的单站RCS计算结果如图6所示。
令等离子体电子数密度为0.8×1018m-3;等离子体的碰撞频率为100GHz,在导弹外壳涂覆等离子体δ分别为2,5,7mm条件下,电磁波沿鼻锥方向入射时飞机1单站RCS计算结果如图7所示。
综合飞机1的仿真结果,可发现:
a)涂覆等离子体材料后,飞机的隐身效果主要表现在沿鼻锥的后向散射方向,在较宽频带的频率范围内,飞机的后向RCS衰减可达十多个分贝,迎面格斗时能起到先敌发现的效果;电磁波沿飞机尾部照射时,涂覆飞机的RCS略有降低,隐身效果不明显甚至没有效果。
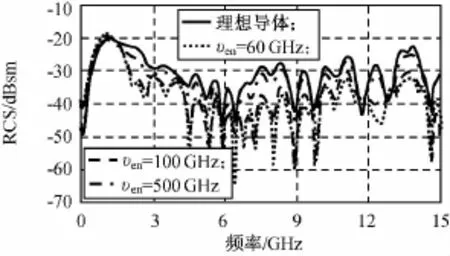
图6 等离子体碰撞频率变化时飞机1单站RCSFig.6 Monostatic RCS of plane model under various plasma collision frequency
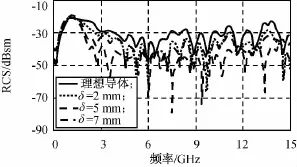
图7 不同等离子体厚度时飞机1单站RCSFig.7 Monostatic RCS of plane model under various plasma thickness
b)在低频时飞机的隐身效果很差或不具有隐身效果,即使涂覆等离子体层,隐身效果仍不佳。这是因为对较低的频率,因等离子体的高通滤波器性质,电磁波进入等离子体内部的深度并不大,而且在较低频率的衰减量也较小,故吸收也不大,理论上用米波雷达就可探测到隐身飞机。
c)在中频时,均匀非磁化等离子体对电磁波的衰减较明显(可达十多个分贝)。但在较高频率时,均匀非磁化等离子体对电磁波的衰减小于中频,甚至没有作用。对较高的频率,由于电磁波的频率远离等离子体的截止频率,导致等离子体中的电子无法跟随电磁波电场的变化,因此等离子体对电磁波的衰减也不大。
d)对沿鼻锥方向入射的电磁波,隐身效果随等离子电子数密度增大而变好,随等离子碰撞频率增大而减弱,因此需选择合适的等离子体参数使目标的隐身效果达到最佳。
e)等离子体厚度对飞机模型的RCS有影响。随着等离子体涂覆厚度增加,等离子体涂覆层能更有效地衰减入射电磁波,且对低频段电磁波的吸收效果也有明显改善。因此在不改变飞机气动外形前提下,适当增大等离子体层厚度对增强飞机的隐身效果有益。
3 结束语
本文研究了具有色散三特性的非磁化等离子体的三维ZFDTD算法。给出了等离子体的ZFDTD方法,分别导出了非磁化等离子体的极化电流密度的辅助方程,将间接Z变换算子用于极化电流密度的辅助方程中,得到极化电流密度与电场、磁场两分量间的迭代关系。用推导的方法计算了典型目标的后向RCS,同相关文献的结果吻合较好。另外,用该法计算了非磁化等离子体涂覆复杂目标的后向RCS,分析了等离子体参数变化对飞机RCS的影响。
[1] 庄钊文,袁乃昌,刘少斌,等.等离子体隐身技术[M].北京:科学出版社,2005.
[2] 晏 明,许 金,余锡文.非均匀非磁化等离子体柱的ZTFDTD分析[J].海军工程大学学报,2009,18(3):18-22.
[3] YAN M,SHAO K R,HU X W,et al.Z-transformbased FDTD analysis of perfectly conducting cylinder covered with unmagnetized plasma[J].IEEE Trans Magnetics,2007,43(6):2968-2970.
[4] QIAN Z H,CHEN R S.FDTD analysis of magnetized plasma with arbitrary magnetic declination[J].International Journal of Infrared and Millimeter Waves,2007,28(1):157-167.
[5] 刘少斌,莫锦军,袁乃昌.各向异性磁化等离子体JECFDTD算法[J].物理学报,2004,53(3):783-787.
[6] XU Li-jun,YUAN Nai-chang.JEC-FDTD for 2-D conducting cylinder coated by anisotropic magnetized plasma[J].IEEE Microwave Wireless Components Lett,2005,15(12):892-894.
[7] LIU Shao-bin,YUAN Nai-chang,MO Jin-jun.A novel FDTD formulation for dispersive media[J].IEEE Microwave Wireless Components Lett,2003,13(5):187-189.
[8] 刘少斌,刘 崧,洪 伟,等.等离子体隐身技术[M].北京:科学出版社,2010.
[9] WANG S,SHAO Z H,WEN G J.A modified high order FDTD method based on wave equation[J].IEEE Microwave Wireless Components Lett,2007,17:316-318.
[10] LIU S,LIU M,HONG W.Modified piecewise linear current density recursive convolution finite-difference time-domain method for anisotropic magnetized plasmas[J].IET Microwave Antennas Propag,2008,2(7):677-685.
[11] WEEDON W H,RAPPAPORT C M.A general method for FDTD modeling of wave propagation in arbitrary frequency-dispersive media[J]. IEEE Transactions on Antennas and Propagation,1997,45(3):117-125.
[12] PAKHOMOV A G.Comparative effects of extremely high power microwave pulses and a brief CW Irradiation on pacemaker function in isolated frog heart slices[J].Bioelectromagnetics,2000,21:245-254.
[13] YANG H W,CHEN R S,ZHOU Y C.SO-FDTD analysis on magnetized plasma[J].International Journal of Infrared and Millimeter Waves,2007,28(7):751-758.
[14] YANG Hong-wei.A FDTD analysis on magnetized plasma of Epstein distribution and reflection calculation[J].Computer Physics Communications,2009,180:55-60.
[15] 麻来宣,张 厚,张晨新.改进磁化等离子体SOFDTD方法[J].河南师范大学学报(自然科学版),2010,38(1):75-77.
[16] 麻来宣.等离子体隐身关键技术研究[D].西安:空军工程大学,2010.
[17] 杨丽霞.复杂介质电磁散射的FDTD算法及相关技术研究[D].西安:电子科技大学,2006.
