基于粒子群优化的再入飞行器在线轨迹规划

陈上上，何英姿、2，刘贺龙

（1.北京控制工程研究所，北京 100190；2.空间智能控制技术重点实验室，北京 100190）

0 引言

航天飞机再入制导取得了巨大成功，但其采用的参考剖面离线规划与在线跟踪的制导策略，不仅设计过程费时费力，而且难以自主应对异常事件的发生，常需要人的干预［1］。为提高第二代可重复使用飞行器的自主飞行能力，从而提高安全性、可靠性，同时降低成本，美国航空航天局与美国空军分别发起了先进制导与控制计划、综合自适应制导与控制计划［2－3］。在线轨迹规划是提高自主飞行能力的一个关键，受到了广泛关注。轨迹规划的基本问题是根据飞行任务的飞行条件和技术要求，寻找一条某种性能指标最优而又不违背各种约束的飞行轨迹。考虑实时性要求，在线轨迹规划时一般对再入运动模型进行简化，结合解析计算与简单数值计算得到近似最优解。MEASE等将航天飞机的二维轨迹规划扩展到三维，轨迹规划问题分为轨迹长度问题与轨迹曲率问题：解决轨迹长度问题时，先基于简化的运动模型得到轨迹长度的解析表达形式，再通过补偿纵程偏差修正总航程，最后用牛顿法迭代至满足终端约束；处理轨迹曲率问题时，用解决长度问题获得的阻力加速度剖面，计算相关侧向加速度幅值，再积分航迹方位角与横程的微分方程，通过搜索得到最小终端横程误差对应的倾侧角反转点［4－6］。陆平等用伪平衡滑翔条件，将强约束、非线性规划问题转为两个一维参数搜索问题，用割线法解决了在线优化问题［7］。SCHIERMAN等用能量多项式函数拟合了高度剖面，将运动方程降阶，显著减少了数值优化问题的搜索维数，最终用非线性规划解决了数值优化问题［8］。

上述数值优化过程多采用传统优化方法，问题复杂度增加时易陷入局部极值；优化指标为单一的航程偏差，优化结果对模型参数摄动、环境不确定性的适应性较差。PSO方法实现简单，全局搜索能力强，在再入轨迹规划应用中受到关注［9－11］。本文对一种基于PSO的再入飞行器在线轨迹规划方法进行了研究。

1 问题描述

忽略地球扁率影响，RLV再入3自由度运动方程为

式中：r为地心距；θ为经度；φ为纬度；v为飞行器相对地球的速度；γ为航迹倾角；ψ为航迹方位角（北偏西为正）；μ为地球引力常数；σ为倾侧角；ωe为地球自转角速度；D，L分别为阻力加速度和升力加速度，且

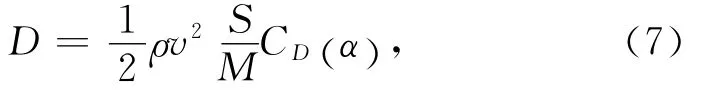
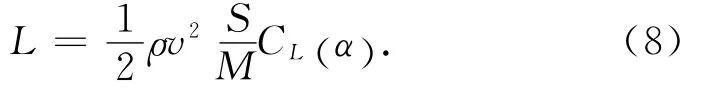
此处：ρ为大气密度；M为飞行器的质量；S为参考面积；CD为阻力系数；CL为升力系数；α为攻角。各状态量几何关系如图1所示。与航天飞机类似，本文研究的飞行器气动系数CD，CL只与α有关。

图1 再入几何关系Fig.1 Geometry of entry flight

采用指数大气密度模型

式中：ρ0为海平面大气密度；h为飞行高度；hs为大气归一化高度。

一般来说，再入过程中需要实时满足的约束主要有热流率约束、法向气动过载约束、动压约束、零倾侧角时的平衡滑翔约束，分别为

式中：为热流率；cq为热流传递系数；n，m为常数，一般取n＝0.5，m＝3；nz为法向气动过载；g0为地面的重力加速度；q为动压。

另外，再入过程还需考虑总吸热量约束

以及航程偏差约束

式中：Rpre为解析预测航程；Rtogo为待飞航程。

本文研究的再入轨迹在线规划问题描述为：给定初始条件、过程约束式（10）～（13）、吸热量约束式（14）、终端位置约束式（15），考虑模型参数摄动、环境不确定性和异常事件发生等情况，在线寻找参考轨迹，使如下条件成立：

a）参考轨迹对应的状态变量r，θ，φ，v，γ，ψ与控制量σ，α满足运动方程式（1）～（6）；

b）过程约束、吸热量约束、终端位置约束得到满足；

c）控制量σ，α及其一阶导数与二阶导数不能超出姿态控制系统要求范围，整个飞行过程中都能实现姿态配平。

2 参考剖面设计

本文轨迹规划的方案为：

a）离线设计攻角参考剖面（α－v）；

b）在线规划阻力加速度（D－v）参考剖面；

c）根据D－v剖面，实时得到参考升阻比，进而得到控制量σ的大小；

d）σ的符号根据瞄准误差或通过一维搜索最优反转点确定［1、7］。

其中，D－v剖面在线规划是轨迹规划的核心，是本文的研究重点。方案中的c），d）已十分成熟，本文未做讨论。

2.1 攻角剖面设计

再入α－v剖面设计主要考虑减轻防热系统重量、末端能量管理段的制导需求，以及姿态配平要求。本文用离线优化设计α－v剖面，再入过程中α－v剖面不再变化，根据地速直接得到参考攻角。本文对所研究的再入飞行器离线设计的α－v剖面如图2所示。

图2 参考攻角剖面Fig.2 Angle of attack profile

α－v剖面的函数形式为

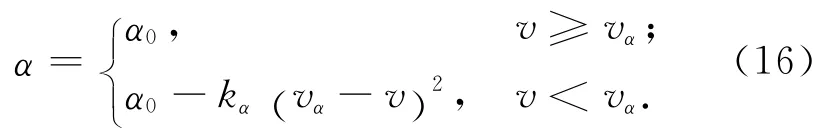
式中：α0，vα，kα为设计参数。

α－v剖面确定后，在D－v平面内，可直观地用再入走廊边界替代过程约束式（10）～（13），航程与总吸热量也可解析表示为D与v的关系式，而D与v能通过测量系统或在线辨识实时获得，因此基于阻力加速度的制导方法在实际工程中得到了广泛应用［1、4－6］。

2.2 过程约束转化

由式（7）、（10）～（13）易得D－v平面内各过程约束的表达式为

由上述约束形成了D－v平面内的再入走廊，其中热流、法向气动过载和动压约束共同构成了再入走廊的上边界（Du－v），平衡滑翔条件则独自构成了再入走廊的下边界（Dl－v），如图3所示。

图3 再入走廊与参考阻力加速度剖面Fig.3 Reentry corridor and reference drag acceleration profile

2.3 吸热量计算

再入的初始下降段大气稀薄，气动力作用很小，一般采用固定倾侧角指令策略，不单独设计参考剖面。该段结束后（高度约80km），才开始设计参考剖面。一般D－v剖面由温控段、伪平衡滑翔段、常值阻力段和过渡段4段组成，其中温控段包括两个相接的二次型段。文献［1］给出了各段航程的解析表达式，本文给出各段吸热量的表达式。

吸热量的一般表达式为

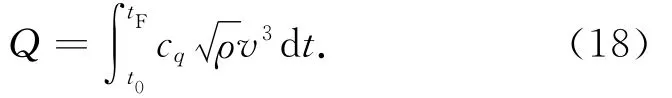
式中：t0，tF分别为初始与终端时间。再入过程中航迹倾角很小，故

将式（7）、（19）整理后代入式（18）得

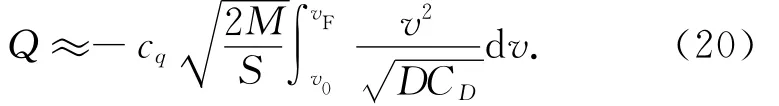
式中：v0，vF分别为初始与终端速度。

因CD只与α有关，由图2、3可知：温控段、伪平衡滑翔段与常值阻力段阻力系数为常值，仅过渡段的阻力系数随地速而变。

为便于表述，对D－v参考剖面的各节点依次编号：0为再入点；1为第一个二次型段起点；2为第一个二次型段终点，第二个二次型段起点；3为第二个二次型段终点，伪平衡滑翔段起点；4为伪平衡滑翔段终点，常值阻力段起点；5为常值阻力段终点，过渡段起点；6为过渡段终点。设vi，Di为节点i（i＝0，1，…，6）处的地速与阻力加速度。

a）温控段

第一个二次型D－v剖面函数形式为

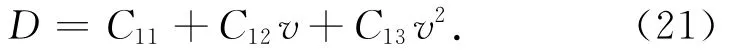
式中：C11，C12，C13为设计参数。

将式（21）代入式（20），可得第一个二次型段吸热量表达式为

（a）当C3＞0时，

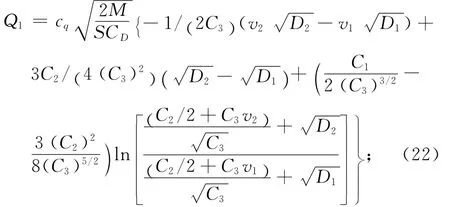
（b）当C3＝0，C2≠0时，

（c）当C3＜0时，

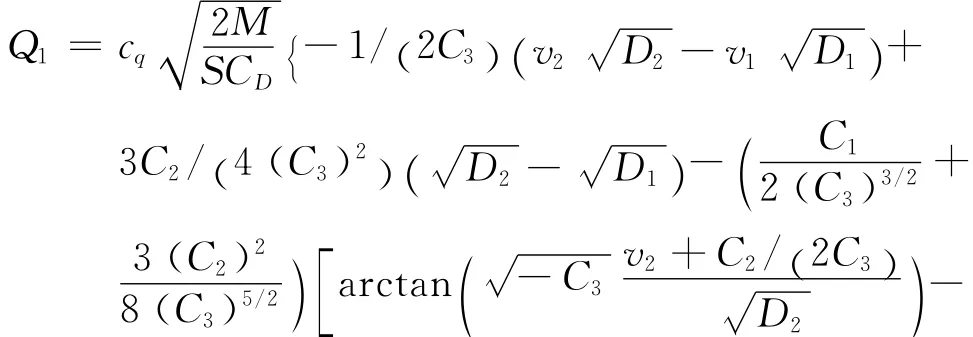
第二个二次型D－v剖面函数形式为

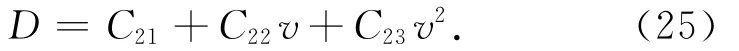
式中：C21，C22，C23为设计参数，该段吸热量Q2的表达式与式（22）～（24）类似。

b）伪平衡滑翔段

该段D－v剖面的函数形式为

c）常值阻力段

该段D－v剖面的函数形式为

式中：C4为设计参数，把式（28）代入式（20），可得该段吸热量表达式为

d）过渡段

该段D－v剖面的函数形式为

式中：C5为设计参数；E为飞行器的能量，且E＝gh＋0.5v2；E6为过渡段末端能量。

求解该段吸热量时，先拟合得h－v关系式

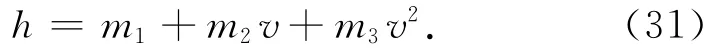
式中：m1，m2，m3为拟合系数。由式（30）、（31）可得

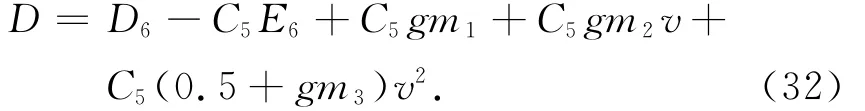
再拟合得CD－α关系式

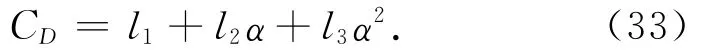
式中：l1，l2，l3为拟合系数。

根据式（16）、（20）、（32）、（33）可得该段吸热量表达式为

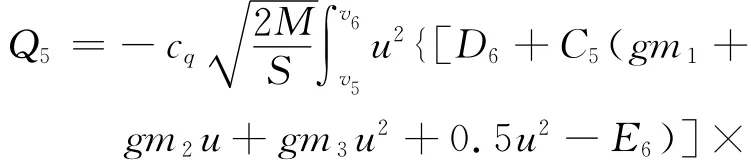
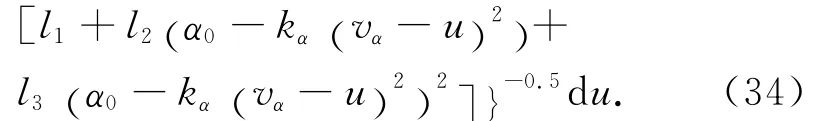
式（34）不便于进一步解析计算，D－v剖面优化时可通过简单的数值积分得到该段吸热量。

在再入走廊内设计的D－v剖面能自动满足各种过程约束；用本文的吸热量表达式与文献［1］给出的航程表达式，可预测吸热量与航程误差；若吸热量与航程误差不满足要求，则需要重新设计参考剖面，重复上述过程至满足实际需求。通常，上述迭代过程可用优化方法完成。

3 优化问题形成

参考剖面参数有9个，其中温控段6个，其它3段各1个，若直接进行优化会十分复杂。如以各段端点坐标为待优化参数，根据任务要求及参考剖面连续性与光滑性要求，可减少优化参数数，提高优化效率。

3.1 参考剖面简化设计

初始下降段采用固定倾侧角飞行，通常不再调整v1，D1；为保证过渡段的航程调整能力，v5通过离线优化设计，不做在线调整；另外，根据任务要求，一般v6，D6为固定值。

除上述5个节点坐标固定外，其余参考剖面节点坐标均可在线调整，调整基本原则为

a）节点及由节点连接的参考剖面应完全在再入走廊内；

b）再入航程与总吸热量应满足任务需求；

c）各段相接的节点处尽量保证连续性与光滑性。

根据上述原则，为保证初始下降段与第一个二次型段的平滑过渡，设计D－v剖面时应保证两段交点处斜率相等，设均为k1。因初始下降段不做调整，故k1为已知。

同理，为保证其它各段的连续性与光滑性，则有

式中：

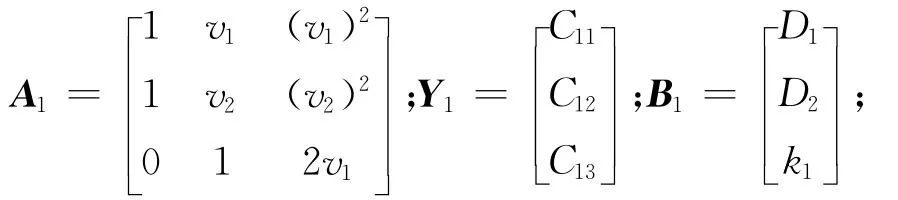
由式（35）～（37）可发现，参考剖面的9个参数能由X唯一确定：给定k1，v1，D1，v5，v6，D6，X后，由式（35）可得C11，C12，C13，之后由式（36）可得C21，C22，C23，K3，D3，由式（37）可得v4。

3.2 参考剖面优化

当α－v剖面确定后，相应的再入走廊也随之确定。但由于模型参数摄动及环境不确定性的存在，设计再入走廊时应保守一些，另外为保证一定的侧向机动能力，参考剖面不应过于接近再入走廊下边界。

由上述分析已知：4个节点参数可唯一确定D－v剖面，因此也决定了参考剖面与标称再入走廊边界的最小距离。本文在优化指标中考虑此最小距离、总吸热量和航程偏差。

由式（17）可得再入走廊上下边界的D－v函数分别为

由前述已知，参考剖面参数由X唯一确定，参考阻力加速度可表示为X，v的函数，即

取设计优化目标为

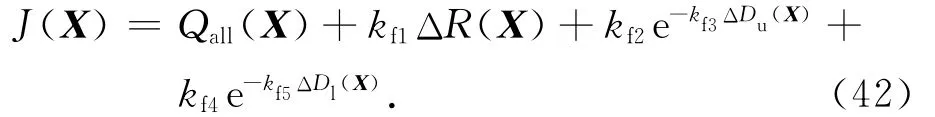
式中：Qall为总吸热量，且Qall＝Q1＋Q2＋Q3＋Q4＋Q5；ΔDu为参考剖面与标称再入走廊上边界的距离，且 ΔDu＝min ［fu（v）－f（X，v）］；ΔDl为与下边界的距离，且ΔDl＝min ［f（X，v）－fl（v） ］；kf1，kf2，kf3，kf4，kf5为设计参数。最后两项设计为指数形式，其值随参考剖面与走廊边界距离的减小而迅速增大，而参考剖面与走廊边界的距离增大到一定程度后，这两项不再起作用。实际应用时，根据任务情况与飞行器自身特性可合理选取式（42）中的某几项组成优化目标。考虑再入走廊边界约束以及节点坐标之间的大小关系，最终的优化问题为

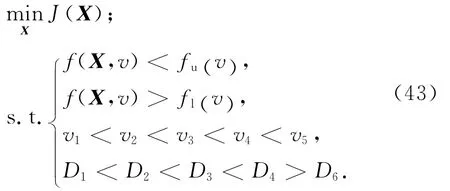
4 基于改进PSO的在线剖面优化

图4 二维PSO示意图Fig.4 Two－dimensional PSO

PSO算法中的m个粒子一直并行搜索。在每次迭代过程中，记录每个粒子的迄今最优位置pi（k），通过比较获得整个粒子群迄今最优位置pg（k）。通过速度更新与位置更新得到下一步的搜索方向与位置分别为

本文定义使优化目标式（42）数值最小的位置为最优位置。参数搜索的更新速度应与该参数范围相匹配，否则，更新速度太快易引发搜索振荡，更新速度太慢搜索时间太长，不利于在线应用。为此，本文将式（44）改进为

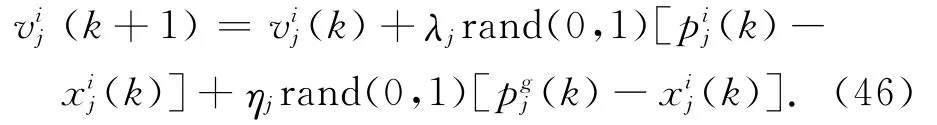
式中：λj，ηj分别为控制个体认知分量和群体社会分量相对贡献的第j维学习率，可根据优化量的搜索范围设计，改进后每维待优化量都有与之匹配的学习率。

算法流程如图5所示。

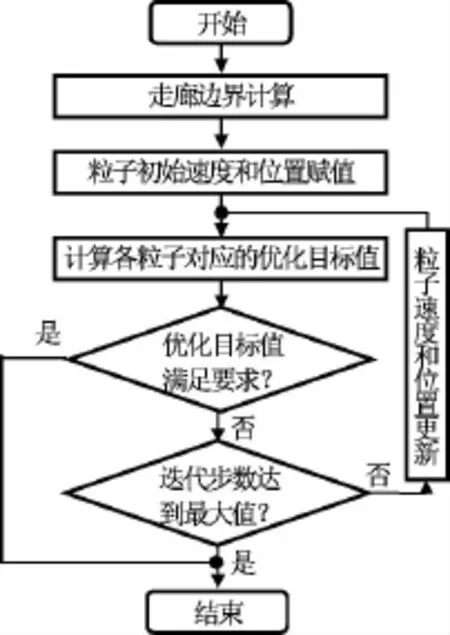
图5 基于PSO的在线剖面优化算法流程Fig.5 Flowchart of onboard profile planning algorithm based on PSO

5 仿真

对本文使用的RLV及相关飞行任务，过渡段参考剖面易接近再入走廊下边界，从而导致末端侧向机动能力不足，因此需在优化指标中考虑过渡段参考剖面与走廊下边界的距离。取优化指标

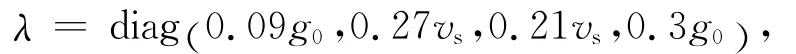
表1 优化参数初值Tab.1 Initial values of optimized parameter

采用上述设计参数，遍历考查异常时间发生时飞行任务更改为短航程与长航程时参考剖面优化结果。短航程下的指标优化结果为Qall＝0.717Qmax，ΔR＝0.310km，ΔDl＝1.398m／s2；长航程下的指标优化结果为Qall＝0.777Qmax，ΔR＝1.211km，ΔDl＝1.166m／s2。优化的D－v剖面分别如图6、7所示。由图可知：两种情况下过渡段参考剖面对应最小倾侧角均为30°左右，侧向机动能力得到了保证，设计的参考剖面与再入走廊上下边界都保持一定距离，在异常事件发生时能应对一定的模型参数摄动和环境不确定性。

在普通计算机Windows XP系统中用Matlab仿真，优化算法平均耗时6s，能满足在线规划要求。另外，根据实际需求，在C环境中对程序进行优化可进一步提高该方法的实时性。

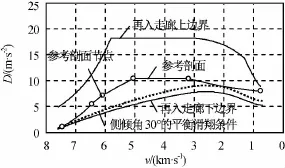
图6 短航程优化结果Fig.6 Optimization result of short range simulation

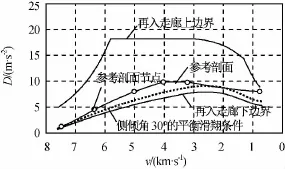
图7 长航程优化结果Fig.7 Optimization result of long range simulation

6 结束语

本文对基于改进PSO的再入飞行器的在线轨迹规划方法进行了研究。考虑了再入过程约束、终端位置约束、总吸热量约束、模型参数摄动与环境不确定性影响，保证了再入末端的侧向机动能力，提高了异常事件发生时优化轨迹对模型参数摄动以及环境不确定性的适应能力。仿真验证了方法的实时性。

［1］ HARPOLD J C，GRAVES C A.Shuttle entry guidance［J］.Journal of the Astronautical Sciences，1979，27（3）：239－268.

［2］ HANSON J M.A plan for advanced guidance and control.technology for 2nd generation reusable launch vehicles［C］／／ AIAA Guidance，Navigation，and Control Conference and Exhibit. Monterey：AIAA，2002：1－9.

［3］ SCHIERMAN J D，WARD D G，HULL J R，et al.Integrated adaptive guidance and control for re－entry vehicles with flight test results［J］.Journal of Guidance，Control，and Dynamics，2004，27（6）：975－988.

［4］ MEASE K D，CHEN D T，TEUFEL P，et al.Reduced－order entry trajectory planning for acceleration guidance［J］.Journal of Guidance，Control and Dynamics，2002，25（2）：257－266.

［5］ SARAF A，LEAVITT A，CHEN D T，et al.Design and evaluation of an acceleration guidance algorithm for entry［J］.Journal of Spacecraft and Rockets，2004，41（6）：986－996.

［6］ LEAVITT A，MEASE K D.Feasible trajectory generation for atmospheric entry guidance［J］.Journal of Guidance，Control and Dynamics，2007，30（2）：473－481.

［7］ SHEN Z J，LU P.Onboard generation of three－dimensional constrained entry trajectories［J］.Journal of Guidance，Control and Dynamics，2003，26（1）：111－121.

［8］ SCHIERMAN J D，HULL J R.In－flight entry trajectory optimization for reusable launch vehicles［C］／／AIAA Guidance，Navigation，and Control Conference and Exhibit.San Francisco：AIAA，2005：1－18.

［9］ 孙增圻，邓志东，张再兴.智能控制理论与技术［M］.北京：清华大学出版社，2011.

［10］ RAHIMI A，KUMAR K D，ALIGHANBARI H.Particle swarm optimization applied to spacecraft reentry trajectory［J］.Journal of Guidance，Control and Dynamics，2013，36（1）：307－310.

［11］ 谢富强，吴 浩，唐灵灵.基于粒子群算法的飞行器再入轨迹优化［J］.计算技术与自动化，2008，27（4）：72－75.