速度突变状态下高温热管的毛细极限与性能分析
2015-12-31刘伟强
李 波,刘伟强
(国防科学技术大学 高超声速冲压发动机技术重点实验室,湖南 长沙 410073)
0 引言
高超声速飞行器飞行过程中,机体前端、翼前缘等驻点区域会有严重的气动加热,由驻点热流的相关计算可知:当在高度24km下以7马赫飞行时,半径20mm的前缘鼻锥上热流密度可达2~3MW/m2,壁面温度达1 400K[1]。严重的气动加热会导致飞行器外形烧蚀、结构强度和刚度等发生改变,严重影响飞行器的正常飞行,高超声速气动热是高超声速飞行器发展的关键技术之一[2]。传统的高超声速飞行器防热方式存在结构复杂、重量大、气动外形不能保持等缺陷,而疏导式防热作为一种半被动防热方式,通过高导热率材料或高效传热元件将驻点区域的热量快速传导至低温区,借助大范围的低温散热面以对流和辐射的方式释放热量,达到降低驻点区域表面温度,满足结构完整性的需求,具有结构简单、可重复利用性强的特点[3]。
高导热率材料或高效传热元件作为疏导式防热结构的核心部件,需要具备优良的定向导热能力。导热能力很强的铜导热系数300~400W/(m·K),一种经过专门研究而获得的高导热率石墨烯碳材料的导热系数可达5 000W/(m·K)左右,而热管作为一种高效的传热元件,其等效导热系数是铜的100倍(30 000~40 000W/(m·K)),较碳材料的导热系数高一个量级[4]。因此在高超声速飞行器防热结构中,热管由于其超高的等效导热系数和较低的技术难度会有广泛应用。20世纪70年代,国外对用热管冷却高超声速飞行器前缘进行了研究[5]。国内相关研究较少,文献[6]提出用高温热管实现飞行器前缘的疏导式热防护,并用电弧风洞分析了高温热管的冷却机制;文献[7]研究了高温热管的疏导式防热效果,证明前缘内置高温热管对驻点区域良好的热防护性能,并设计了一种飞行器的层板式前缘结构。现有用热管结构冷却高超声速飞行器前缘研究多基于飞行器以恒定的马赫数在固定的高度巡航飞行,在此条件下飞行器前缘热管结构处于稳定工作状态,不受外界干扰。实际飞行过程中,飞行器的姿态和加速度会出现各种改变,在大加速的作用下热管内部工质的流动性会受到很大影响,热管的毛细极限也会极大降低,热管能否保持正常工作也值得深入研究。为此,本文基于已有用热管进行疏导防热的研究,根据推导加速状态下热管的毛细极限方程,分析了加速度的影响。
1 高温热管工作过程
高温热管是疏导式防热结构中的核心部件,可将驻点区域的高热流快速传递至低温区而无需外加动力,是一种非常高效的传热元件。热管依靠内部工质的相变和循环实现传热,具高导热性、优良的等温性、热流方向可逆性等特性。热管的工作过程主要是从蒸发段吸收热量,通过内部工质相变传热将热量输送到冷凝段,实现热量转移。其工作原理如图1所示:液态工质在蒸发段受热气化,蒸发段气体压力增大,受压力的作用,变为气态的工质通过绝热段向冷凝段流动,并逐步冷凝为液态,将热量释放。由于蒸发段液态工质不断减少,冷凝段液态工质不断增加,在毛细结构的毛细力作用下,液态工质会产生回流,由此形成热管的循环过程。

图1 热管工作原理Fig.1 Working principle of heat pipe
2 典型热管结构物理模型
一种用于飞行器前缘疏导式防热的V型热管结构的物理模型如图2所示。因上下结构的对称性,图2只可出了上缘部分。该热管结构内嵌或包覆在飞行器前缘,V型的尖端部分处于前缘热驻点附近,通过两侧热管的疏导作用将驻点处的热流传输到低温处,借助低温散热面将热量释放,降低驻点区域表面温度。对此热管结构,文献[8]认为稳态工作时热管上下缘的工作性能相同,用对称处理方法,对其防热性能进行了建模分析,证明了其良好的疏导式防热效果。
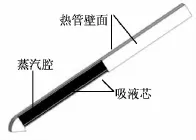
图2 前缘热管结构物理模型Fig.2 Physical model of heat pipe structure of leading edge
该热管结构采用了轴向矩形沟槽式吸液芯,金属锂作为传热工质,结构参数为:热管截面(长方形)尺寸16mm×36mm;头部曲率半径R为38.1mm;翼弦向长度R+L为(38.1+400)mm;半锥角θ为15°;槽道深度h为0.762mm;槽 道 宽 度w为0.457mm。其中的槽道参数是参考文中已有的给定数据。
3 速度突变时热管毛细极限
热管工作介质的循环主要依靠毛细吸液芯结构与工作液体产生的毛细力提供动力,而毛细结构为工质循环提供的毛细力有限,这使热管的最大传热量受限,该限制常被称为热管的流体动力极限或毛细极限。
在单根矩形沟槽内液态锂弯月面形状的变化如图3所示。图中:冷凝段和蒸发段的固液接触角分别为θc,θe;对应的弯月面曲率分别为Rc,Re。工质从冷凝段向蒸发段流动过程中,固液接触角逐渐减小,弯月面曲率半径也逐渐减小,而相对应的毛细压力也不同,导致蒸发段和冷凝段间产生压力差,此压力差即为液态锂的回流动力。

图3 毛细吸液芯内弯月面Fig.3 Meniscus in capillary wick
对矩形槽道,其有效毛细半径rc=w。由拉普拉斯-杨氏方程可知热管槽道内的毛细压力

式中:σ为液态锂的表面张力。存在关系

冷凝段的毛细头Δpc和蒸发段的毛细头Δpe分别为
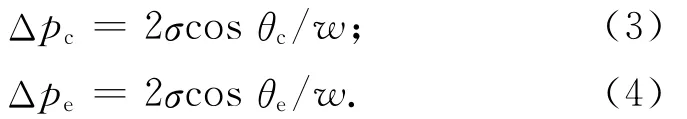
则热管两端的毛细头压差

极限情况下,当θc=90°,θe=0°,Δp取得极大值

通常情况下,热管要正常工作须满足毛细压降大于蒸汽压降、液体压降与重力压降的总和。处于飞行器中的热管,还需考虑飞行器加速度a的额外影响。因此,热管正常工作需满足

式中:下标v、l、g、a分别表示蒸汽、液体、重力、飞行器加速度。
Δpv,Δpl一般随热载荷增大而增加,而 Δpmax取决于吸液芯结构形式,其最大值见式(6)。
因热管倾斜产生的重力压降

式中:ρl为液态工质密度;l为热管长度;φ为热管轴线与水平方向的夹角;g为当地重力加速度。
设飞行器加速度a的方向与热管轴向夹角为φ,则由此产生的加速度压降

对层流不可压缩的蒸汽流动,假设热载荷在蒸发段和冷凝段是均匀分布的,由于加速度的影响作用和重力加速度影响作用类同,结合已有的毛细极限计算公式可知,存在加速度时热管的毛细极限Qc,max计算公式为

式中:加速度或重力阻碍冷凝回流时,“±”取-,加速度或重力利于冷凝回流时,“±”取+;Fl为沟槽中液态工质的摩擦因数,且

Fv为蒸汽腔中气态工质的摩擦因数,且
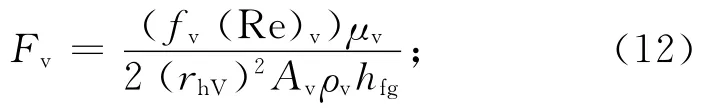
leff为热管有效长度;dv为热管蒸汽腔直径。此处:K为吸液芯的渗透系数;AW为吸液芯截面积;fv(Re)v为蒸汽通道的阻力系数;hfg为液态工质的汽化潜热;ρv为气态工质密度。
由推导的毛细极限公式可知,重力项和加速度项对热管的毛细极限有很大的制约作用,而飞行试验过程中会出现重力和加速度同时阻碍热管内工质冷凝回流的情况,这时热管的毛细极限会极大降低,甚至为负值,热管将不能正常工作。对加速飞行段加速度值是5g~10g的高超声速飞行,对热管毛细极限的影响作用将会更大。
4 速度突变时热管性能
金属锂在温度为1 000K左右时,液态密度为气态的500多倍,且气态工质的流动性很强。因此,飞行器存在速度突变时对热管的影响主要表现为阻碍液态工质从冷凝段回流。
以单根槽道内的液态工质回流为例,加速度项量级为重力项的5~10倍,而重力项量级为摩擦力项的约20倍,分析过程中忽略摩擦力的影响,最大毛细压差只需克服重力和加速度的影响,则
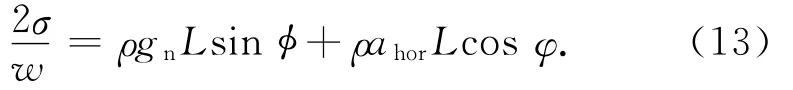
式中:ahor为水平加速度;gn为当地重力加速度,因飞行高度对重力加速度的影响较小,取gn=9.8m/s2;L为理论的毛细吸液长度。
热管参数中,前缘曲率半径相对槽道总长较小,且热管为轴向沟槽结构,槽道与热管轴向平行,为便于分析,将单根槽道简化为如图4所示的模型。其中:x为水平轴方向;y为竖直方向。定义上下缘槽道分别为槽道1、2,两者间夹角30°,长度453mm。计算处理时认为热管的蒸发段、绝热段和冷凝段的长度相等,各占热管总长度的1/3。假设热管正常工作时槽道内液态工质的回流长度大于绝热段长度(151mm),取温度1 000K时工质锂的物性参数计算。

图4 单根沟槽分析模型Fig.4 Simplified model of a single groove
由式(13)可算得无飞行倾角时,不同水平加速度下槽道内理论毛细吸液长度如图5所示。由图可知:加速度为0m/s2时,槽道1的理论毛细吸液长度趋近无限大,这与液态工质在重力作用下自然回流相符;槽道2的理论毛细吸液长度约1 200mm,足以满足热管工作循环需要。这也表明无速度突变时上下缘热管都处于正常工作状态,在导热分析时进行对称处理也是合理的。由两条吸液长度曲线与151mm等值线的交点可知:当飞行器以加速度约2g飞行时,由于工质回流的限制,热管将处于极限工作状态;当飞行器加速度大于5g后,槽道1、2的理论毛细吸液长度曲线趋于重合,但上下缘热管同时处于失效状态。
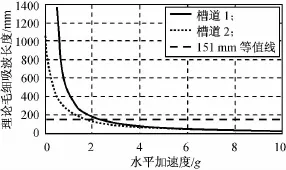
图5 不同水平加速度下理论毛细吸液长度Fig.5 Theoretic capillary imbibition length under various horizontal angles
为分析热管在失效时,由倾角变化产生的上下缘热管工作情况(上下缘热管具不对称性),飞行器以恒加速度3g飞行时,不同V型热管对称轴与水平X轴间的夹角(-π/6~π/6)下槽道理论毛细吸液长度如图6所示。由图可知:在给定的水平倾角变化范围内,倾角较大时槽道1的毛细吸液长度仍满足上缘热管的工作需求,但下缘热管不能正常工作,这说明结构对称的V型热管在实际工作过程中具不对称性。不对称性主要出现在飞行器加速度大于2g条件下,其原因一是重力会促进上缘热管冷凝段液态工质回流,而阻碍下缘热管液态工质回流,二是加速度不会一直为水平,角度变化时对上下缘热管的影响不同。

图6 不同水平倾角下理论毛细吸液长度Fig.6 Theoretic capillary imbibition length under various horizontal accelerations
以上计算是基于静态的分析,忽略了热管工作时内部蒸汽和液体阻力的作用,而这些因素会导致热管内液态工质的回流长度更小。同时,在热管失效时会造成前缘结构温度上升,液态锂温度也会同样上升,而液态锂的表面张力随温度上升会减小,这就导致热管的毛细力进一步减小,热管实际状况会更恶化。因此,应用热管进行疏导式防热的过程中,飞行器的实际飞行状态对热管有很大影响。
5 结束语
本文对速度突变状态下高温热管的毛细极限与性能进行了分析。结果发现:飞行器在飞行过程中,由于巨大的加速作用,热管的毛细极限会极大降低,液态工质的吸液长度也会变短,造成疏导效果降低,实际应用中热管的长度设计需综合考虑疏导效果与加速度的影响间的关系。加速度对热管毛细极限的影响主要表现为毛细芯的吸液能力,对轴向沟槽吸液芯结构的热管,应选择毛细能力强的槽道设计方案,在满足热管内工质回流量的前提下保证有足够的毛细力。对前缘结构的V型热管,加速状态下上下缘热管的极限参数不同,下缘热管更易失效,分析中需分别考虑。应用热管进行疏导式防热过程中,针对加速度的影响,可改进热管结构,用长短交替的V型热管替代单一的结构。当飞行器巡航飞行时长热管可保证良好的疏导防热效果,在飞行器出现较大速度突变时短热管也能正常工作,同时也间接增加长热管的蒸发受热段长度,在一定程度上保证长热管的工作。
[1] 李会萍,董 葳.高超声速再入钝头体表面热流计算[J].上海航天,2010,27(2):19-20.
[2] 梁 强,张平峰,许 泉.基于CFD复杂外形飞行器气动加热高效算法[J].上海航天,2013,30(5):14-15.
[3] DONOVAN B,CHANG D,GOTTSCHLICH J M,et al.Missile fin heat pipe cooling[R].AD 358663,1998.
[4] PETERSON G P.An introduction to heat pipe:modeling,testing,and applications[M].New York:John Wiley and Sons,1994.
[5] PEEPLES M E,REEDER J C,SONTAG K E.Thermostructural applications of heat pipes[R].NASA CR 159096,1979.
[6] 姜贵庆,艾邦成,俞继军,等.高温热管在疏导式热防护技术中的应用[C]//第十一届全国热管会议论文集.威海:中国科学院工程热物理研究所,2008:72-78.
[7] 刘伟强,孙 建,聂 涛,等.一种飞行器的层板式前缘结构[P].中国:201310311505.5,2014-03-10.
[8] 孙 健.高超声速飞行器前缘疏导式热防护结构的工作机理研究[D].长沙:国防科学技术大学,2013.
