天基光学观测GEO空间目标定轨方法研究

孙 杰，李 冬

（中国人民解放军91550部队，辽宁 大连 116023）

0 引言

GEO卫星具有相对地球同步的轨道特征，在导航定位、授时、跟踪与数据中继、导弹预警等领域的应用不断增多，对非合作的GEO空间目标进行日常监视与定轨，对增强空间态势感知能力有重大意义。天基光学监视系统利用天基卫星搭载的可见光相机对GEO空间目标进行探测成像，不受地域限制和气象条件限制，只需要一颗卫星就可完成对整个地球同步轨道带的覆盖。天基卫星还能从不同的方位观测GEO空间目标，站星几何变化大，观测几何结构好，定轨精度高，用天基光学观测方式对GEO空间目标进行高精度定轨成为空间目标监视的一个重要发展方向［1－4］。

1996年，美国在空间中段实验卫星（MSX）上搭载可见光传感器（SBV），开始对天基空间目标监视技术展开演示验证［1、5］。SBV的一个重要任务是确定GEO空间目标轨道，完成在编目标的编目维持和更新，其定轨过程分为初轨确定和轨道改进两个阶段，初轨确定的作用是在目标发现阶段识别目标和引导传感器跟踪目标，经过数个观测弧段的积累，进入了轨道改进阶段，定轨精度迅速提升。文献［6］提出了初轨计算的单位矢量法，将拉普拉斯初轨计算方法的条件方程组形式作变换，使条件方程组中不再出现两两相减的形式，不会损失有效数字，提高了定轨精度。文献［7］研究了考虑摄动时的单位矢量法，扩展了单位矢量法的使用范围。文献［8］给出了一种摄动条件下长弧段初轨计算的单位矢量法，该法既可适于长弧段，也可适于短弧段，计算收敛性较好。与经典Laplace法相比，单位矢量法的优点有计算精度高、稳定性好、收敛速度快等，从而被广泛用于初轨计算，但该法中条件方程组的求解多采用最小二乘法，忽略了条件方程组噪声项的统计特性，故不能给出最优解。引入约束总体最小二乘法（CTLS）用于求解单位矢量法的条件方程组，能充分利用条件方程组噪声项的统计特性获得最优解，从而可提高天基光学观测条件下的初轨确定精度［9］。轨道改进中，天基卫星与GEO空间目标相对几何变化较大，观测量的系统误差易辨识，可将系统误差作为待估量而与观测量分离。本文以SBV为参考，对天基光学观测条件下的GEO空间目标轨道确定方法（包括初轨确定方法和轨道改进方法）进行了研究。

1 GEO空间目标初轨确定

1.1 初轨确定的单位矢量法

天基卫星的可见光传感器能获取GEO空间目标的赤经和赤纬，在地心惯性系中，它们分别为空间目标相对天基卫星的方位角和俯仰角。设观测时刻ti的赤经和赤纬为 （αi，δi）；天基卫星和空间目标在地心惯性系中的位置矢量分别为Ri＝［XiYiZi］T，ri＝ ［xiyizi］T；目标相对天基卫星的方向

距离为ρi。由图1所示的几何关系，有

图1 天基卫星与GEO空间目标的几何关系Fig.1 Geometry relation between space－based satellite and GEO object

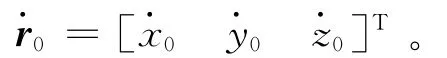
用文献［6］的单位矢量法构造单位矢量

将式（1）中ri在r0，处作FG级数展开，得

式中：fi，gi为时刻ti的FG级数，均为关于r0，的函数。用式（2）、（3）分别点乘式（4）两端，得单位矢量法的条件方程组

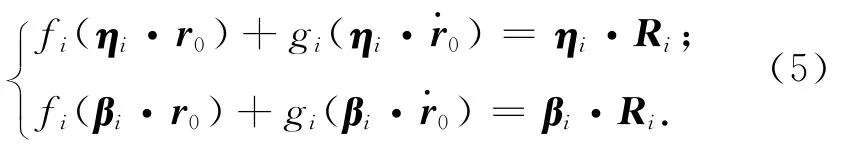
设观测弧段有观测量m组，条件方程组式（5）可表示为

式中：

A，b均受噪声干扰，方程组无解，常用最小二乘法迭代求解X。

1.2 求解条件方程组的约束总体最小二乘法

令C＝［Ab］，则条件方程组式（6）变为

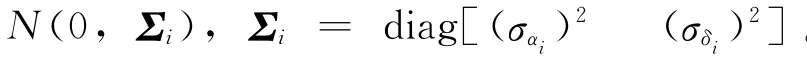
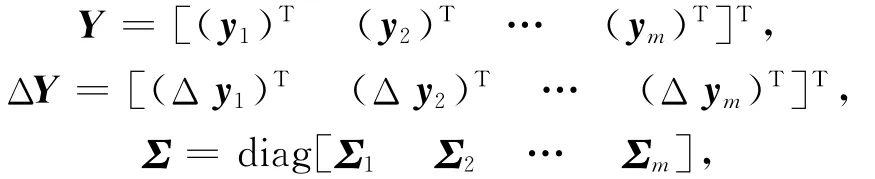
设Y的真值为Y＊，则 ΔY＝Y－Y＊，令u＝Σ－0.5ΔY，则u服从标准正态分布。C为Y的函数，记为C（Y），将C（Y＊）在Y处展开得

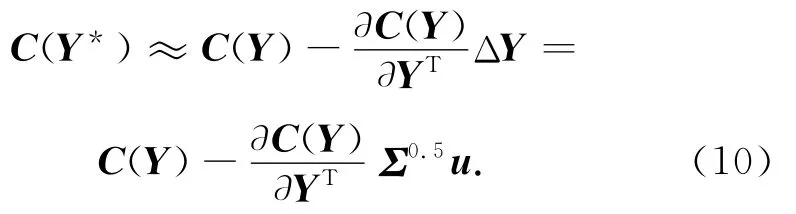
这样，方程式（10）的约束总体最小二乘问题为约束优化问题

约束条件为

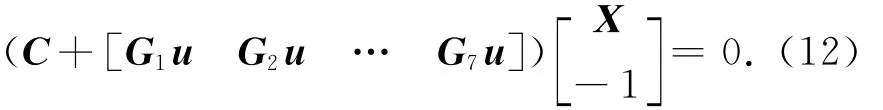
式中：Gj为准对角阵，且Gj＝diag［Gj1…Gjm］。此处：Gji（j＝1，2，…，7，i＝1，2，…，m）为Gj的第i个对角子块矩阵。由式（7）、（9）可得

式中：

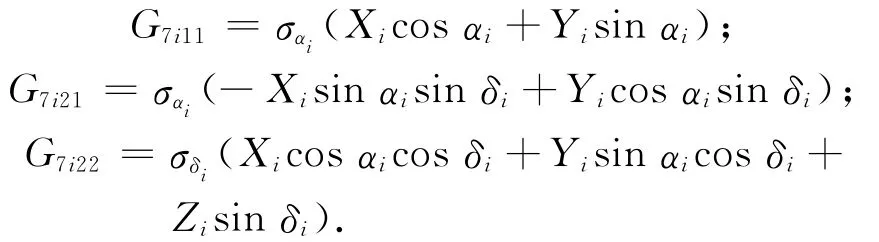
G1i，G2i，G3i中的fi换成gi即为G4i，G5i，G6i。

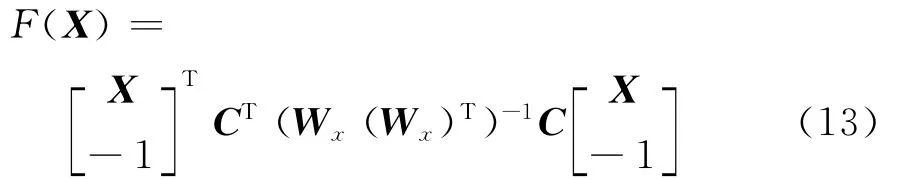
极小化的变量X。由式（13）可求出F（X）关于X的梯度和二阶导数矩阵，这样便可用收敛速度较快的牛顿法求F（X）的极值［10］。实验表明迭代初值的选取严重影响算法的收敛性，如选取不当，易造成迭代发散。经实验检验，文献［11］中消除平凡解的初值计算方法能保证约束总体最小二乘法的收敛性。

2 GEO空间目标轨道改进

轨道改进中，GEO空间目标需考虑的摄动力主要有J4项地球非球形引力、日月三体引力和太阳光压摄动力，其它摄动力相对微弱，本文忽略不计。天基卫星轨道一般为极地轨道，与GEO空间目标的相对几何变化较大，观测几何较好，轨道改进易得测角资料中的系统误差估计，本文对每个观测弧段估计赤经和赤纬的常值系统误差。

令轨道改进中GEO空间目标的状态变量

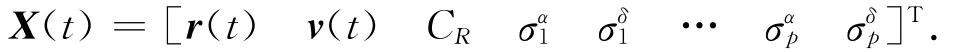
式中：Gi（X0，t0，ti）为时刻ti的测量真值；i＝1，…，N。此处：N为轨道改进中测量采样点数。令

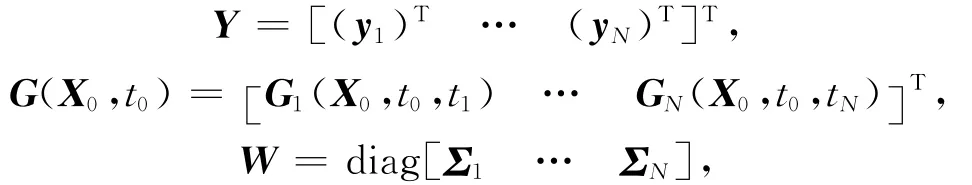
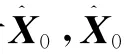
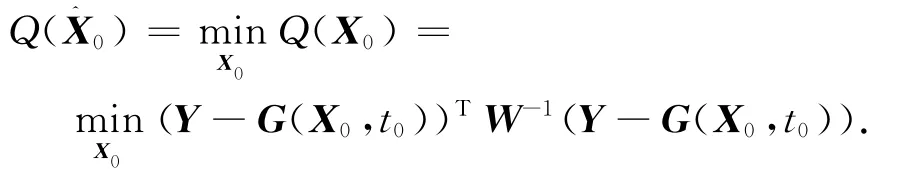
由可得时刻t0空间目标的位置和速度估计，从而完成空间目标的轨道确定，同时也能获得光压系数和测量系统误差的估计。本文用高斯牛顿迭代法计算，迭代公式为

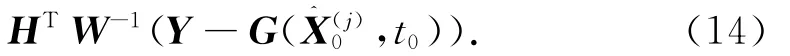
3 仿真实验

取卫星轨道根数半长轴、偏心率、倾角、升交点赤经、近地点幅角和平近点角分别为a，e，i，Ω，ω，M，则第二类无奇点轨道根数为a，i，Ω，ξ，η，λ，其中ξ＝ecosω，η＝－esinω，λ＝M＋ω。仿真中，设天基卫星的轨道为极地轨道，天基卫星和GEO空间目标初始时刻的第二类无奇点轨道根数见表1。GEO空间目标真实轨道的动力学模型采用20×20阶地球引力场模型、日月引力模型、太阳光压模型、固体潮模型和海潮模型，轨道改进中的动力学模型采用4×4阶地球引力场模型、日月引力模型和太阳光压模型，仿真时长为86 400s，蒙特卡罗仿真500次。因地球遮挡和光照条件的影响，天基卫星不能对GEO空间目标连续观测，能观测空间目标的弧段有14个，如图2所示，总观测时间61 478s。

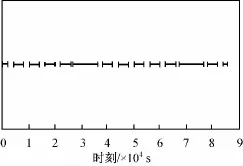
图2 GEO空间目标的观测弧段Fig.2 Observation arcs for GEO object

初轨确定的测角资料选择第一个观测弧段，时长35min，采样间隔5s，在测量噪声（随机误差）分别为15″，30″条件下仿真，最小二乘法（LS）和约束总体最小二乘法（CTLS）所得轨道根数均方根（RMS）误差见表2。由表可知：约束总体最小二乘法的初轨精度相对最小二乘法有所提高，这是因为最小二乘法忽略了条件方程组噪声项的统计特性，但精度提高幅度较小，这是条件方程间的统计相关性较弱的缘故。

轨道改进的测角选择全部可观测弧段，采样间隔1s，待估参数35个，即GEO空间目标的位置速度矢量、太阳光压系数和每个弧段内两个测元的系统误差，轨道改进的迭代初值为初轨确定的结果。500次蒙特卡罗仿真实验结果表明：初轨确定的结果能使轨道改进收敛，系统误差的估计误差不超过2.8%。不同测量误差条件下位置 （x，y，z）和速度（vx，vy，vz）的均方根误差见表3。由表可知：随机误差相同时，系统误差越大，定轨精度越高，这是因为系统误差较大时，易将系统误差与其他误差分离，系统误差的估计精度较高。

表1 天基卫星和GEO空间目标的轨道根数Tab.1 Obit roots of space－based satellite and GEO object

表2 初轨确定轨道根数的均方根误差Tab.2 RMS error of obit roots for preliminary orbit

表3 轨道改进位置速度的均方根误差Tab.3 RMS error of position and velocity for orbit improvement

4 结束语

本文研究了天基光学观测条件下的GEO空间目标定轨方法。初轨确定时先将单位矢量法的条件方程组求解转为一个约束总体最小二乘问题，再转为无约束优化问题，最后用牛顿法迭代求解。仿真结果表明：与最小二乘法相比，约束总体最小二乘法的初轨计算精度有所提高。轨道改进采用非线性最小二乘法同时解算空间目标的轨道参数和测元的系统误差，仿真结果表明系统误差的估计误差不超过2.8%，轨道改进的收敛性能好。

［1］ SHARMA J，STOKES G H，Von BRAUN C，et al.Toward operational space－based space surveillance［J］.Lincoln Laboratory Journal，2002，13（2）：309－334.

［2］ 潘晓刚，李济生，段晓君，等.天基空间目标监视与跟踪系统轨道确定技术研究［J］.自然科学进展，2008，18（11）：1226－1239.

［3］ 文援兰，何星星，李 志，等.天基照相跟踪空间碎片批处理轨道确定研究［J］.宇航学报，2010，31（3）：888－894.

［4］ 李 冬，易东云，程洪玮.天基空间目标监视的短弧段定轨技术［J］.宇航学报，2011，32（11）：2339－2345.

［5］ STOKES G H，Von BRAUN C，SRIDHARAN R，et al.The space－based visible program［J］.Lincoln Laboratory Journal，1998，11（2）：205－238.

［6］ 陆本魁，戎鹏志，吴建民，等.人造地球卫星初轨计算的单位矢量法［J］.宇航学报，1997，18（2）：1－7.

［7］ 陆本魁，李剑峰，马静远，等.一种有摄初轨计算的单位矢量法［J］.宇航学报，1999，20（1）：14－20.

［8］ ZHANG J，LU B，MA J，et al.A new method for orbit determination：unit vector method［J］.Science in China Series G：Physics，Mechanics ＆ Astronomy，2009，52（7）：1115－1119.

［9］ ABATZOGLOU T J，MENDEL J M，HARADA G A.The constrained total least squares technique and its applications to harmonic superresolution［J］.IEEE Transactions on Signal Processing，1991，39（5）：1070－1087.

［10］ 粟塔山，彭维杰，周作益，等.最优化计算原理与算法程序设计［M］.长沙：国防科技大学出版社，2002：60－64.

［11］ 甘庆波，马静远，陆本魁，等.一种基于星间方向观测的初轨计算方法［J］.宇航学报，2007，28（3）：619－622.