海上风机单桩基础受船舶撞击的数值研究

第一作者郝二通男，博士生，1987年生

通信作者柳英洲男，博士，教授，博士生导师，1964年生

海上风机单桩基础受船舶撞击的数值研究

郝二通1，柳英洲2，柳春光1

(1.大连理工大学建设工程学部，辽宁大连116024; 2.辽宁工程技术大学建筑工程学院，辽宁阜新123000)

摘要：目前国内没有海上风机受船舶撞击的相关规范和损伤评估标准，以国内某单桩基础海上风机为例，运用LS-DYNA软件从能量变化、最大撞击力和风机响应角度对风机受船舶撞击过程进了分析，并提出面积受损率来评估风机受损程度。分析结果显示：船舶初始动能在分别不超过约35 MJ、35 MJ、25 MJ时，最大撞击力与船舶质量的1/3次方、速度、撞击角度的正弦值成线性关系，超过时线性关系不再明显；面积受损率能合理反映单桩基础的受损区域和受损面积。

关键词：海上风机；单桩基础；撞击力；面积受损率；数值仿真

收稿日期：2013-12-11修改稿收到日期：2014-01-21

中图分类号:TU473.1；TM614文献标志码：A

Numerical simulation of monopile foundation of an offshore wind turbine subjected to ship impact

HAOEr-tong1,LIUYing-zhou2,LIUChun-guang1(1. Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China;2. College of Civil Engineering & Architecture, Liaoning Technical University, Fuxin 123000, China)

Abstract:There are no relevant specification and damage assessment criterion of offshore wind turbine subjected to ship impact in our country now. Here, taking a domestic offshore wind turbine with monopile foundation as an example, the process of the offshore wind turbine stricken by a ship was analyzed by using LS-DYNA in perspectives of energy variation, the maximum collision-force and the response of the offshore wind turbine. The area damage rate was proposed to assess the damage level of the offshore wind turbine. Results showed that the maximum collision-force increases linearly with increase in one-third power of ship mass, velocity and sine of ship collision angle if the initial kinetic energy of the ship is no more than about 35 MJ, 35 MJ and 25 MJ, respectively; the linear relationship is not obvious other wise; the area damage rate can reasonably reflect the damaged field and its area of the monopile foundation.

Key words:offshore wind turbine; monopile foundation; collision-force; area damage rate; numerical simulation

自从1991年丹麦Vindeby海上风电场建立以来，海上风力发电产业得到了飞速发展，截止2012年底，全球已建海上风电累计装机容量已达5 117 MW，其中我国占389.6 MW，仅次于英国(2 948 MW)和丹麦(921 MW)。加之海上航线变密，船舶与海上风电机组(简称风机)发生碰撞概率也随之增加，因此进行船舶与风机基础碰撞研究对风机设计和安全评测非常重要。

由于我国海上风电场发展起步时间较晚，国内对船舶与风机基础结构碰撞的研究较少。李艳贞等[1]将船体看作刚体，考虑船速影响，对导管架基础风机的抗撞性能进行了数值碰撞分析；Dalhoff和Biehl[2-4]建立双层壳油轮、单层壳油轮、集装箱船和散货船的船侧模型，分别与单桩基础、三脚架基础、导管架基础及重力式基础的风机进行了侧面碰撞分析，并从结构的屈曲和稳定性方面得出单桩基础风机安全性最高；Kroondijk[5]选用16万吨油船，分别在满载和空载情况下与风机导管架基础的管连接点和管腿位置进行了数值碰撞，描述了导管架基础的局部屈曲破坏和整体破坏情况。目前国内外已建海上风电场基础形式有：单桩基础、重力式基础、三脚架基础、导管架基础、承台式基础等，其中单桩基础占65%以上[6]，针对国内并没有风机受到撞击的相关规范以及损伤评估的问题，以国内某海上风机场单桩基础设计方案为例，采用不同吨位、不同速度的船舶分别与风机基础进行了正撞和偏撞，并从能量、撞击力、基础受损及风机响应方面进行了分析和讨论。

1工程概况

国内某近海风电场[7]，占海域面积14 km2，布置有34台单机3 MW的风电机，装机容量102 MW。风电场海域水深9.9 m～11.9 m，考虑海床局部冲刷后的水深在15 m左右，基础选用设计方案其中之一的单桩基础，包括钢管桩和钢管过渡连接段，桩径4.8 m，壁厚45 mm，桩长53 m,桩基入土深度41 m，桩尖进入海底粉细砂层中，装顶露出水面2 m～3 m，基础与风机塔架之间过渡连接段为变直径钢管，长7.77 m。3 MW风电机由塔身(上、中、下塔筒)、机舱、轮毂、风叶及电器系统组成，具体参数见文献[8]。风电场海域西侧为某跨海大桥，设有1 000 t、500 t通航孔，其中1 000 t通航孔穿过风电场。根据实际海域过往船舶吨位和航行速度，选用500 t、1 000 t、2 000 t、3 000 t的船舶分别按2 m/s、4 m/s、6 m/s与风机单桩基础进行正撞和偏撞数值模拟。

2数值计算模型

2.1材料本构模型

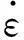
(1)

式中:σs为静态极限屈服应力；C和P为与材料性质有关的常数。

船艏、单桩基础及风机塔身材料均为低碳钢，在碰撞过程中材料应变率很大，所以碰撞分析中必须考虑材料应变率的影响。LS-DYNA提供的非线性塑性材料模型(*MAT_PLASTIC_KINEMATIC[10])能够很好地模拟冲击荷载下的金属材料，该模型就是在Cowper-Symonds关系式基础上建立的，其表达式为：

(2)

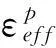
考虑到远离碰撞区域的部件不参与碰撞，为了提高计算效率，船身和船尾用刚体(*MAT_RIGID[10])来模拟，风机的叶片、轮毂、机舱通过在塔架顶施加集中质量来代替。

表1　各部件材料参数

2.2有限元模型

2.2.1船体有限元模型

根据风电场海域实际情况，选用载重量为1000 t的散货船，船艏型式为飞剪型，其尺寸主要参数见表2。碰撞中船舶主要分为碰撞部位(船艏)、非碰撞部位(船身和船尾)两部分。船艏结构包括各层甲板、舱壁等，均通过壳单元来模拟，单元厚度为20 mm，单元尺寸为0.25 m，其有限元模型见图1；船身和船尾用刚体材料通过实体单元来模拟，单元尺寸超过了1 m，通过改变船身和船尾密度来控制船体重心和质量。

表2　船舶主尺度参数表

船体在碰撞前的运动过程中，船体结构和水相互作用必须考虑，一般通过流固耦合模型和附加质量模型[11]来解决，考虑到流固耦合模型将使CPU时间剧增以及主要研究目的，而且附加质量法也得到了很多学者[12-13]验证和认可，船体结构和水相互作用选用附加质量法，附加质量取船体质量的0.05[14]倍。

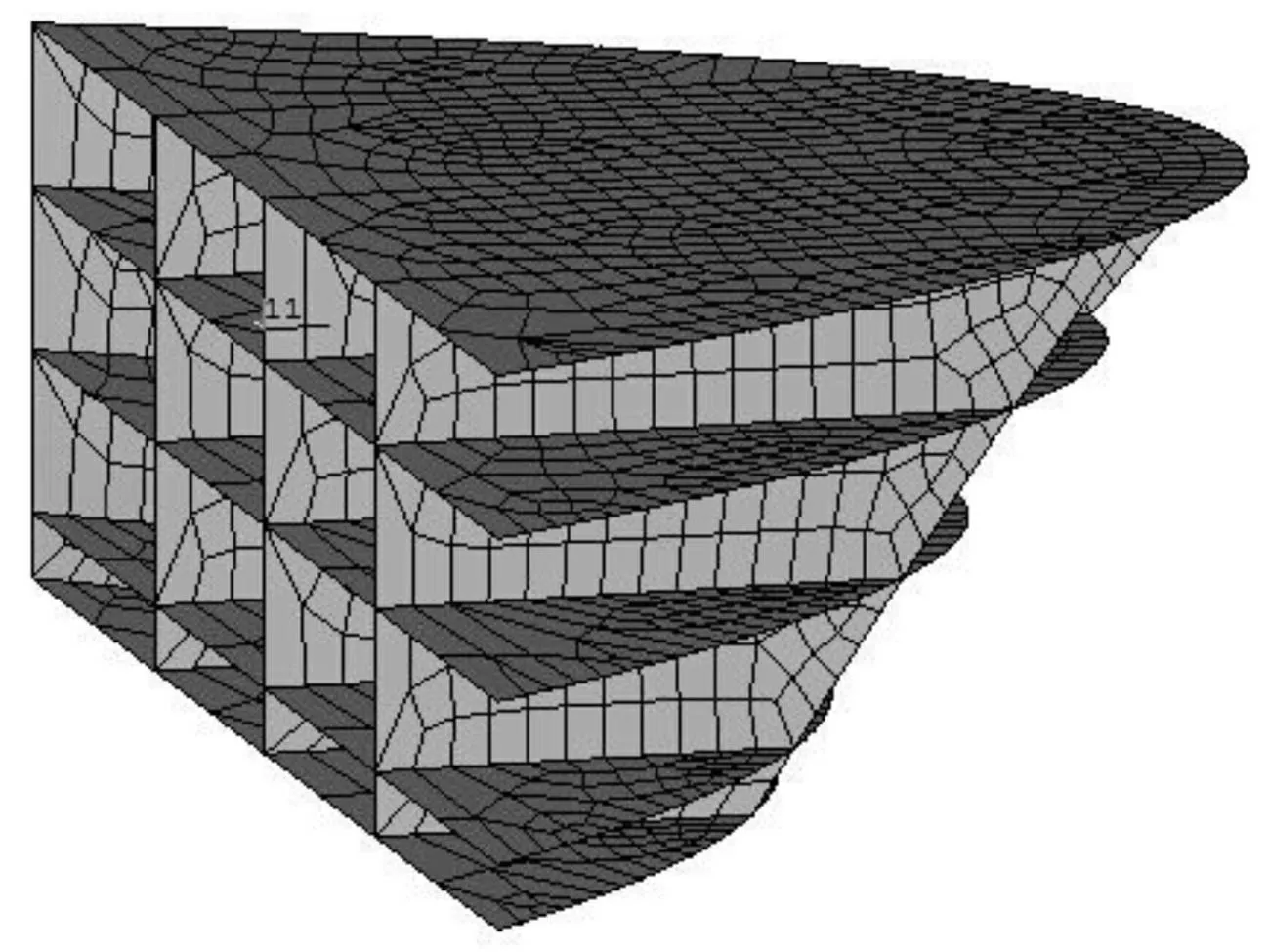
图1　船艏有限元模型(局部剖视) Fig.1 FEM model of bow (Perspective)

2.2.2单桩基础和风机有限元模型

图2　单桩基础和 风机有限元模型 Fig.2 FEM model of monopile foundation and offshore wind turbine

船与风机基础撞击过程中，桩土相互作用方法[15]包括等效桩长法、m法以及非线性抗力位移法。根据《公路桥涵地基与基础设计规范》[16]，桩土相互作用选用较成熟的m法进行简化分析，即桩在海床局部冲刷面下17.4 m处固接处理。钢管桩、过渡段、风机塔身之间固接连接，碰撞区域进行网格细化，尺寸为0.25 m，其余部分为1 m，塔架顶施加叶片、轮毂、机舱的总质量，单桩基础和风机有限元模型见图2。

2.2.3接触定义

为了保证船艏和钢管桩不发生初始接触，船艏前端与钢管桩边缘留出0.6 m的间距。船艏与钢管桩接触选用LS-DYNA提供的自动面面接触(*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE[10])，船艏自身接触为自动单面接触(*CONTACT_AUTOMATIC_SINGLE_SURFACE[10])，由于接触材料均为钢材，动静摩擦系数取0.2[17]。

3计算结果与分析

3.1能量分析

为了保证有限元模型的合理性和计算结果的准确性， 首先从能量角度进行碰撞分析。船与风机碰撞过程

中，船舶初始动能(包括附连水)转化为撞击船与桩基的弹塑性变形能、船舶的剩余动能(包括附连水)、桩基和风机的动能、碰撞摩擦产生的滑移能[18]及计算过程中由于沙漏现象损失的沙漏能[18]；碰撞结束后，风机和桩基在自身阻尼和外界阻尼作用下振动，由于外界阻尼复杂且不影响研究目的，结构仅考虑了自身阻尼(C=a0M，a0=2ξ/ω，ξ为结构阻尼比，钢结构一般取0.02，ω为结构基频，经计算得0.233 58)。图3是初始动能为4.2 MJ、8.4 MJ、16.8 MJ、25.2 MJ船舶与风机基础碰撞的能量变化曲线，图中沙漏能与总能之比均低于1%且能量守恒，说明有限元模型合理及计算结果正确；当碰撞系统的动能达到最低时，即碰撞结束的最后一刻，由图3中(a)、(b)、(c)、(d)对比可知碰撞结束的时刻随初始动能增加在后移，即碰撞持续时间在增加，但均不超过1.5 s，同时碰撞持续时间的增加也造成摩擦产生的滑移能在相应增加；随后动能曲线得到了迅速回升，即船舶在碰撞结束后发生了回弹，从动能回弹与初始动能的百分比(31.58%、22.80%、10.79%、9.72%)可知，随着初始动能的增加，碰撞逐渐由弹性碰撞向塑性碰撞过渡，主要原因是结构的塑性变形量在增加；当系统动能回弹后达到峰值时，此时动能主要由船舶、风机和桩基振动产生；之后风机和桩基振动在阻尼作用下逐渐衰减，从动能振荡情况看出，振荡幅值随着初始动能增加在明显减小，动能减小至零的时间段也在缩短，主要由于初始动能较小(4.2 MJ)时的碰撞持续时间很短(约0.6 s)，为弹性碰撞，碰撞后风机动能振荡明显，随着初始动能增大，碰撞持续时间增加造成风机振动减弱，动能振荡也相应减弱，同时桩基塑性变形增加，屈曲面积增大，结构刚度减小，结构周期变长，耗能增加，动能减小速度也相应加快。

图3　船舶与风机碰撞能量变化曲线 Fig.3 Energy curve of ship-offshore wind turbine collision

3.2撞击力分析

3.2.1质量对撞击力影响

图4为不同质量船舶(500 t、1 000 t、2 000 t、3 000 t)在一定速度下的正撞撞击力曲线，每条曲线均标注了最大撞击力的大小和时间。曲线开始阶段，结构碰撞属于弹性碰撞，不同吨位船舶的撞击力曲线基本重合，具有一定线性特征；随后曲线出现了很强的非线性波动特征，撞击力每一次峰值的卸载主要由于船艏构件和桩基的受损或失效，最大撞击力也随船舶吨位增大明显增加；从撞击力持续时间角度来观察可知，质量增加明显提高了撞击持续时间，例如，初始动能相同的情况下，船舶甲(m=2 000 t、v=2 m/s )和船舶乙(m=500 t、v=4 m/s)与钢管桩的撞击力持续时间有着明显的提高(1.15 s和0.63 s)，而撞击力却相差不大(7.79 MN和7.59 MN)。

为了更好地分析最大撞击力与船舶质量关系，将最大撞击力与船舶质量进行了拟合，发现最大撞击力与船舶质量的1/3次方具有较好的线性关系(线性关系优于质量的平方根)，见图5，这与挪威公共道路局规定[19]一致，但从图5中也发现，当船舶初始动能超过35 MJ，撞击使结构破坏非常严重时，最大撞击力与船舶质量的1/3次方不再具有线性关系。

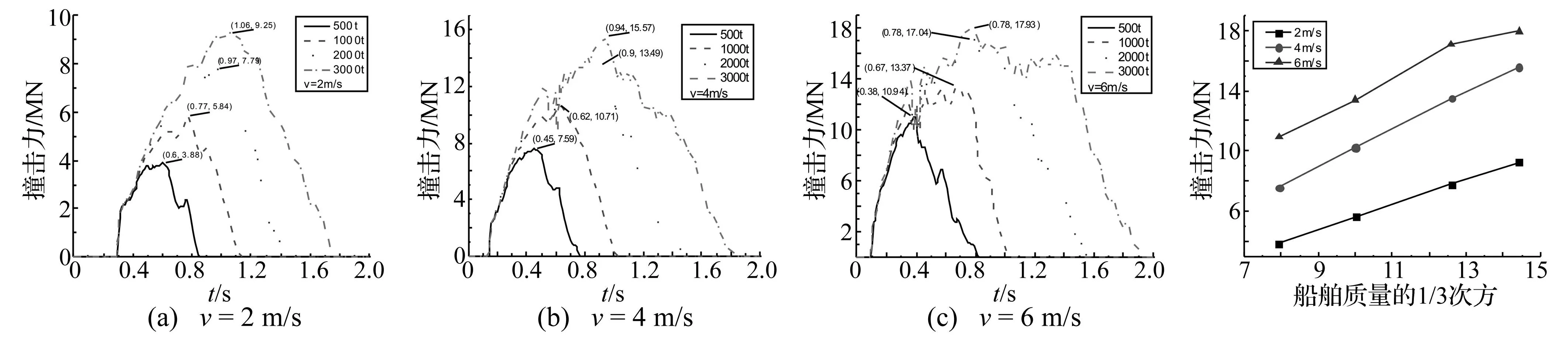
图4 不同质量船舶撞击力曲线Fig.4Collision-forcecurveofshipwithdifferentquality图5 最大撞击力与船舶质量关系Fig.5Relationshipofthemaximumcollision-forceandshipquality

3.2.2速度对撞击力影响

图6为不同速度(2 m/s、4 m/s、6 m/s)船舶的撞击力曲线，由于船艏与风机钢管桩之间有一定间距及船速不同造成撞击力曲线起始点不同，为了能更好观察和分析撞击力曲线，将撞击力曲线起点调至同一点，并对最大撞击力进行标注。同样，曲线开始阶段，结构碰撞属于弹性碰撞，不同速度船舶的撞击力曲线基本重合，具有一定线性特征；随后不同速度船舶的撞击力曲线迅速分开，相比与船舶质量不同更加明显，随着速度增加，曲线非线性波动特征也逐渐显著；撞击持续时间随速度提高的增加并不明显。

为了更好地分析最大撞击力与船舶速度关系，将最大撞击力与船舶速度进行了拟合，发现最大撞击力与船舶速度具有较好线性关系(见图7)，这与国内外桥墩受撞规范[19-22]规定一致，但从图7中也发现，当船舶初始动能超过35 MJ以致结构破坏相当严重时，最大撞击力与船舶速度不再具有明显的线性关系。

图6　不同速度船舶撞击力曲线 Fig.6 Collision-force curve of ship with different velocity

图7　最大撞击力与船舶速度关系 Fig.7 Relationship of the maximum collision-force and ship velocity

3.2.3撞击角度对撞击力影响

船舶与风机撞击分为正撞和偏撞，为了研究偏撞与正撞关系，用船舶速度方向与钢管桩撞击点切线方向夹角来定义撞击角度(见图8)。图9为正撞(90°)、偏2 m撞(66°)、偏4 m撞(42°)下的撞击力曲线，从图9中可以看出，最大撞击力随着撞击角度减小而迅速减小；同一质量和速度的船舶，撞击角度对撞击持续时间影响不大。

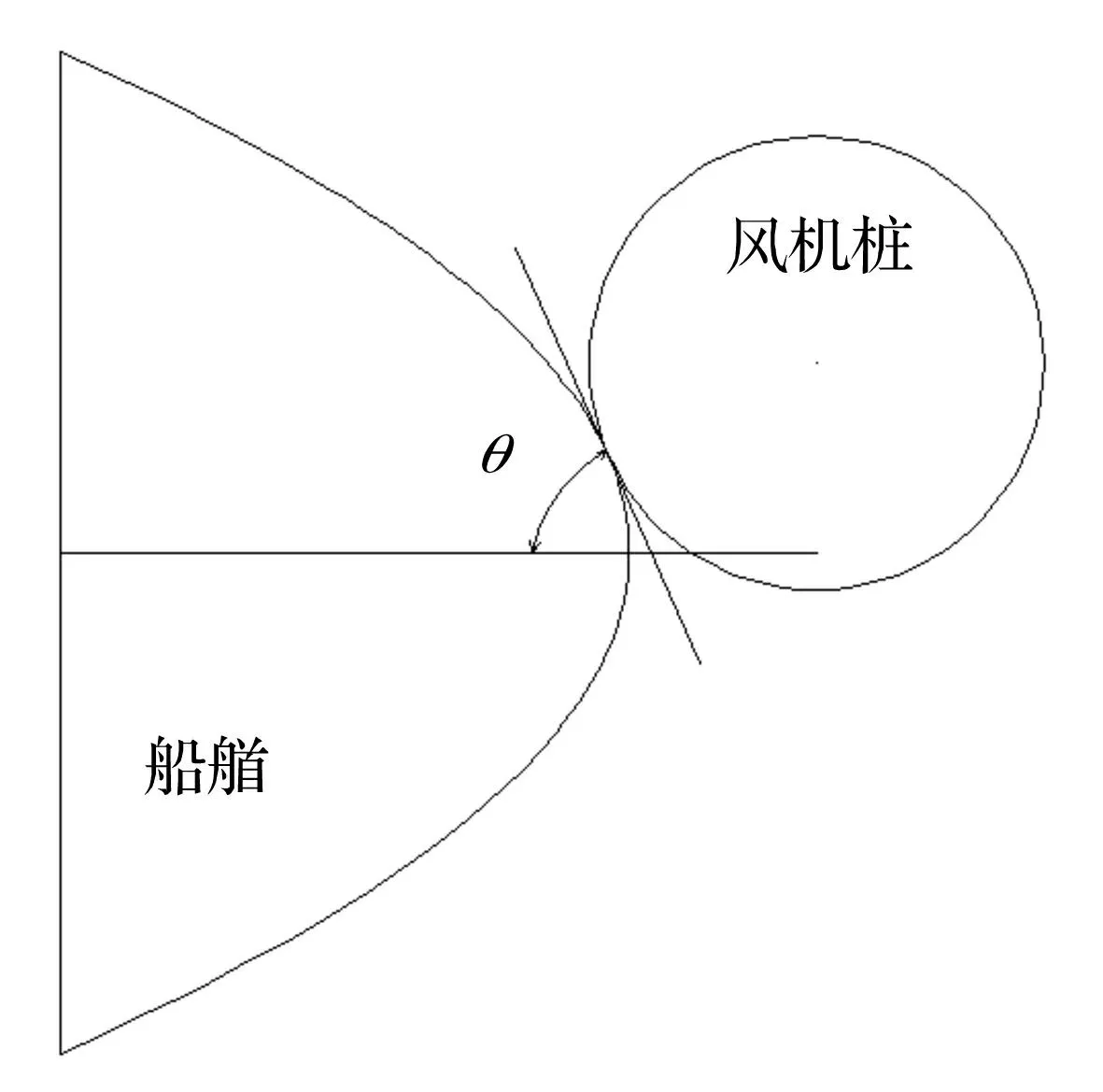
图8　撞击角度示意图 Fig.8 Diagram of collision angle

为了更好地分析最大撞击力与撞击角度关系，将最大撞击力与撞击角度进行了拟合，发现最大撞击力与撞击角度的正弦值具有很好的线性关系(见图10)，这与《铁路桥涵设计基本规范》[20]相符，但同样当船舶初始动能超过25MJ可能导致结构严重破坏时，最大撞击力与撞击角度正弦值的线性关系不再明显。

3.3单桩基础受损分析

3.3.1单桩基础面积受损率

由于单桩基础在风机基础中占有率非常高，达65%以上。而其在海上被撞击后受损程度的定量描述对工程设计者和维修人员很重要， 针对单桩基础几何形状规则以及材料区别于钢筋混凝土，提出面积受损率δ来描述风机被撞后单桩基础的受损程度，公式如下：

图9　不同撞击角度下撞击力曲线 Fig.9 Collision-force curve of ship with different collision angle

(3)

式中:A为碰撞过程中单桩基础(钢管桩和钢管过渡连接段)的屈曲总面积，σ为结构的Von Mises等效应力，σ0为材料的屈服强度，tstart、tend分别为碰撞开始和结束时刻；At为单桩基础总面积，本文At为631.979 3 m2。

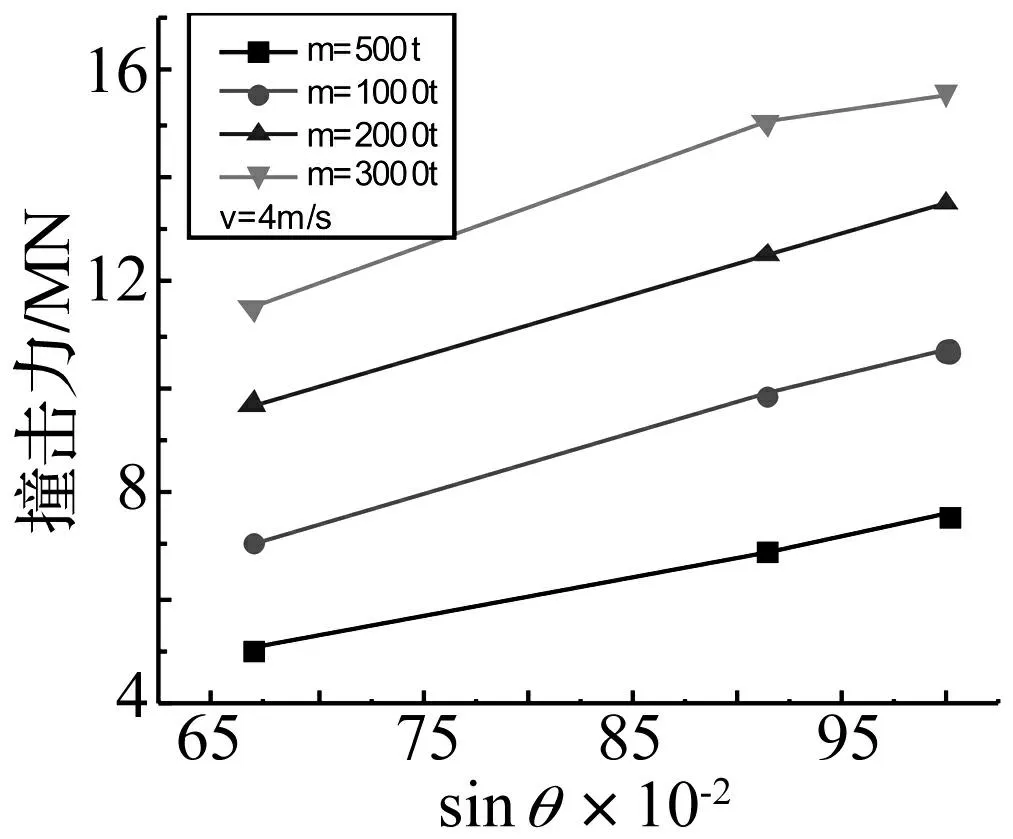
图10　最大撞击力与撞击角度关系 Fig.10 Relationship of the maximum collision-force and collision angle

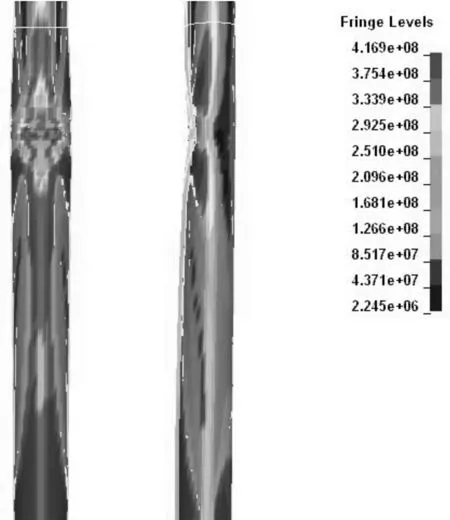
图11　单桩基础等效应力云图 Fig.11 Equivalent stress nephogram of monopile

面积受损率能直观显示风机基础受损区域和受损面积，可以较准确地评估风机基础被撞后的受损程度，有助于工程人员做出经济有效的预防措施和补救措施，图11为风机遭受速度为4 m/s 的3 000 t船舶撞击1.15 s时刻的单桩基础Von Mises等效应力云图(正视和侧视)，该图形象的显示了1.15 s时刻单桩基础的受损区域，通过计算整个受撞过程的单桩基础面积受损率，则可评估其受损程度。

3.3.2面积受损率分析

表3为风机单桩基础在不同吨位、不同速度船舶正撞下的面积受损率，可以发现：相同速度情况下，撞击后风机单桩基础面积受损率随船舶质量增加而提高，且高速提高量比低速提高量大，提高幅度规律不明显；相同质量的情况下，撞击后风机单桩基础面积受损率随船舶速度增大而提高；从初始动能来分析，面积受损率随着初始动能增大而提高，且增大速率随初始动能增加而降低，初始动能相同时，面积受损率几乎一样(工况3和5)；由于面积受损率与质量、速度关系并不是简单线性关系，所以面积受损率与初始动能、质量及速度的详细关系需通过大量数值模拟及结合现场试验来进行讨论分析。

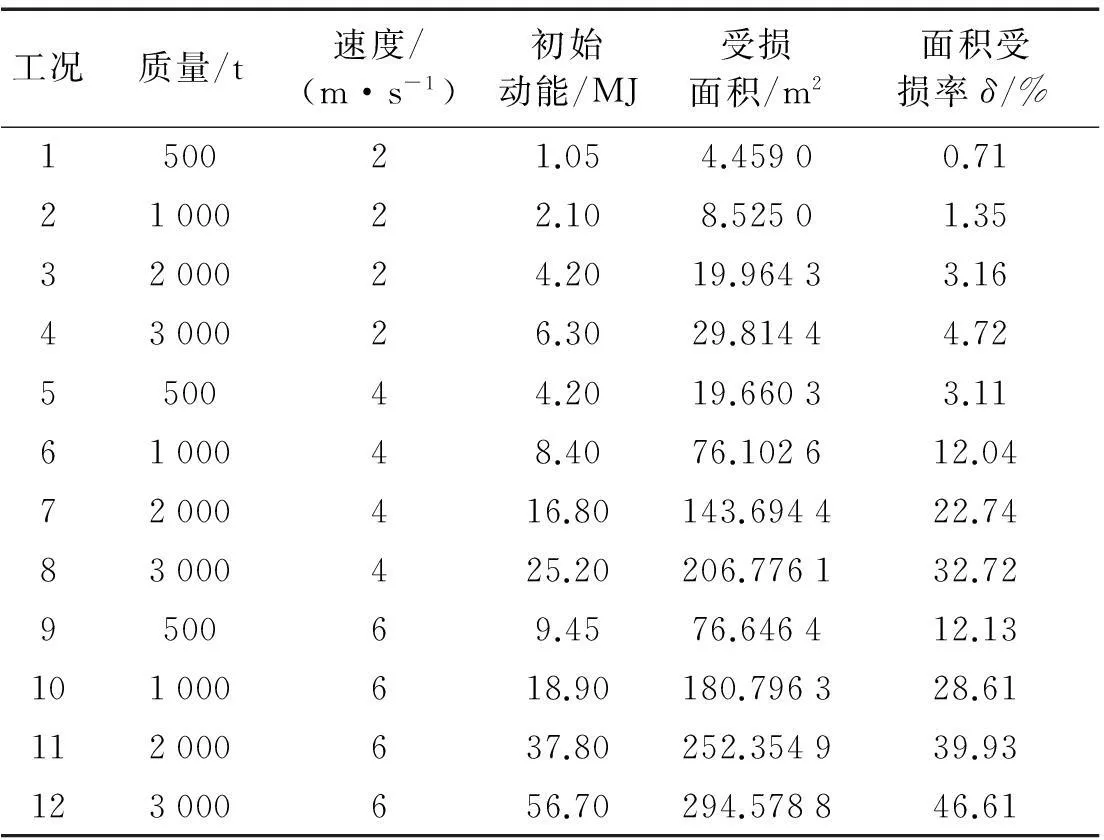
表3　各种工况下单桩基础的面积受损率

3.4风机响应分析

3.4.1机舱加速度响应分析

风机塔架顶机舱、叶片、轮毂等质量非常大(本文为177.1 t)，造成风机受撞击时或撞击后机舱有脱落的危险，因此，分析机舱加速度响应对风机安全非常重要。

图12为不同质量船舶(速度均为4 m/s)与风机撞击时0～2 s内机舱的加速度时程曲线，由图可知：随着船舶质量增大，即船舶初始动能增加，机舱加速度响应明显提高，当船舶质量为3 000 t(初始动能为25.2 MJ)时，机舱最大加速度值可达25.176 m/s2，因此，机舱与塔架连接强度须按过往船舶吨位和航行速度进行碰撞验算。

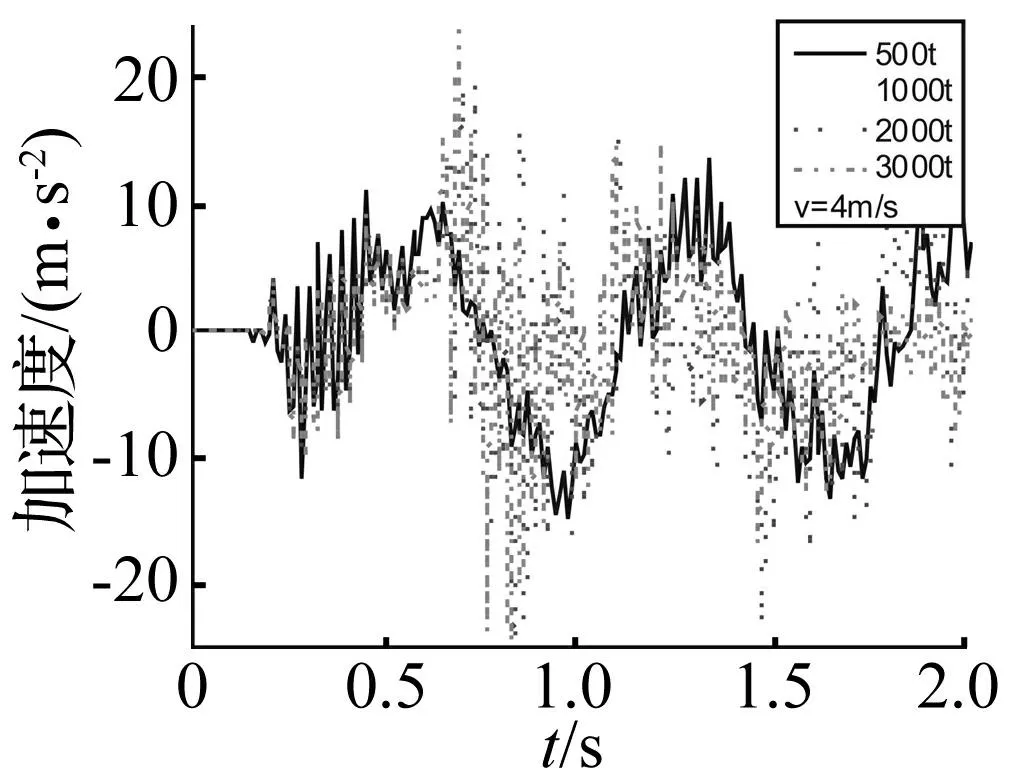
图12　机舱加速度响应时程曲线 Fig.12 Time-history curves of nacelle acceleration

3.4.2塔架变形分析

为分析风机受撞时塔架的整体性能，图13给出工况8下风机塔架不同时刻的位移云图(弯曲变形放大10倍)，从图中可以看出船舶撞击风机的过程中(0～1.75 s)，塔架弯曲变形并不严重，塔架弯曲变形最大出现在撞击结束后塔架的振动过程中，且在3.75 s时塔顶位移达到最大值1.58 m。

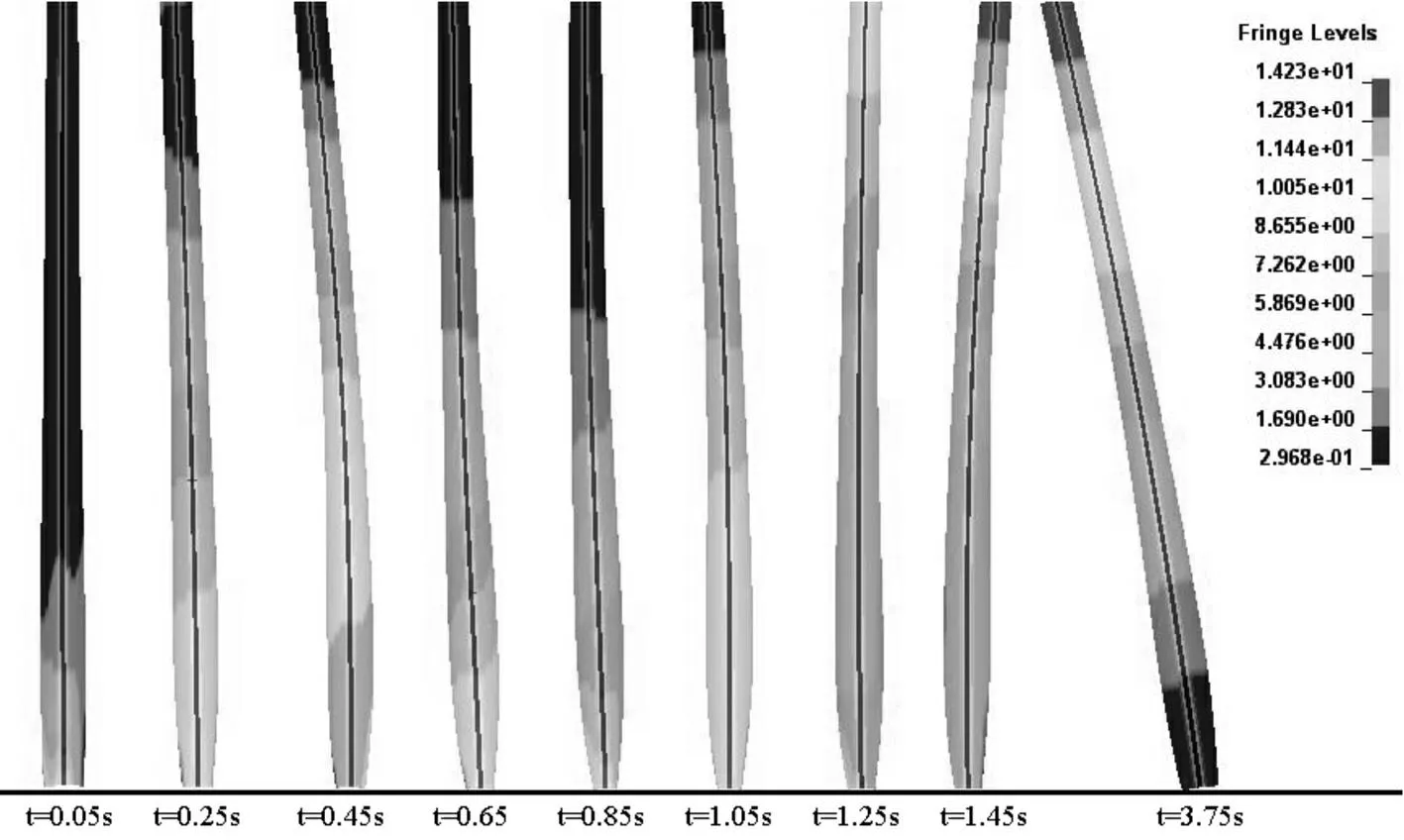
图13　不同时刻塔架位移云图 Fig.13 Displacement nephogram of tower at different time

因此，塔架材料的选择非常重要，刚度大则使机舱加速度过大，增加了机舱脱落的危险性，刚度小则使塔顶位移过大，影响设备正常运行，除了重视塔架材料外，可以考虑基于牺牲非主体结构形变耗能来保护风机整体结构安全的方法，例如在撞击点安装防撞装置。

4结论

(1)在初始动能较小情况下，船舶与风机单桩基础撞击力与船舶质量的1/3次方、船舶速度、撞击角度的正弦值成线性关系，但是当船初始动能分别超过35 MJ、35 MJ、25 MJ时，撞击力与船舶质量的1/3次方、船舶速度、撞击角度的正弦值的线性关系不再明显，以上为风机单桩基础受撞提供了参考。

(2)提出单桩基础面积受损率来描述风机被撞后结构的受损程度，通过计算可知其能很好的反映单桩基础的受损区域和受损面积，为工程人员对风机基础采取经济有效的防护措施提供了依据。

参考文献

[1]李艳贞,胡志强,邹早建. 海上风电站遭遇船舶侧向撞击时的结构动力响应分析[J]. 振动与冲击,2010,29(10):122-126.

LI Yan-zhen, HU Zhi-qiang, ZOU Zao-jian.Structural dynamic response analysis of an offshore wind turbine stricken by a ship in lateral direction[J]. Journal of Vibration and Shock, 2010,29(10):122-126.

[2]Dalhoff P, Biehl F.Ship collision, Risk analysis-emergency systems-collision dynamics[C]//Copenhagen offshore Wind. Hamburg Germany, 2006.

[3]den Boon H, Just H, Hansen P F, et al. Reduction ofship collision risks for offshore wind farms-SAFESHIP[R]. European project, 2004.

[4]Biehl F, Lehmann E.Collisions of ships with offshore wind turbines: calculation and risk evaluation[C]//Offshore Wind Energy. Springer Berlin Heidelberg, 2006: 281-304.

[5]Kroondijk R. High energy ship collisions with bottom supported offshore wind turbines[D]. Trondheim: Norwegian University of Science and Technology, 2012.

[6]王国粹,王伟,杨敏. 3.6 MW海上风机单桩基础设计与分析[J]. 岩土工程学报,2011,S2:95-100.

WANG Guo-cui, WANG Wei, YANG Min.Design and analysis of monopile foundation for 3.6 MW offshore wind turbine[J]. Chinese Journal of Geotechnical Engineering, 2011,S2:95-100.

[7]上海勘察设计研究院. 东海大桥海上风电场工程可行性研究报告[R]. 2006.

[8]华锐风电科技(集团)股份有限公司. 1.5MW、3MW、5MW、6MW系列机组介绍[R]. 2011.

[9]石少卿, 康建功, 王敏，等. ANSYS/LS-DYNA 在爆炸与冲击领域内的工程应用[M]. 北京: 中国建筑工业出版社, 2011.

[10]Gladman B.LS-DYNA®keyword user’s manual-vol. I-version 971[M]. Livermore Software Technology Corporation，2007.

[11]王自力,蒋志勇,顾永宁. 船舶碰撞数值仿真的附加质量模型[J]. 爆炸与冲击,2002,22(4):321-326.

WANG Zi-li, JIANG Zhi-yong, GU Yong-ning.An added water mass model for numerical of ship/ship collisions[J]. Explosion and Shock Waves, 2002,22(4):321-326.

[12]刘建成,顾永宁,胡志强. 桥墩在船桥碰撞中的响应及损伤分析[J]. 公路,2002,10:33-41.

LIU Jian-cheng,GU Yong-ning, HU Zhi-qiang. Response and damage of bridge pier during ship-bridge collision[J]. Highway, 2002,10:33-41.

[13]姜华,王君杰,贺拴海. 钢筋混凝土梁桥船舶撞击连续倒塌数值模拟[J]. 振动与冲击,2012,31(10):68-73.

JIANG Hua, WANG Jun-jie, HE Shuan-hai. Numerical simulation on continuous collapse of reinforced concrete girder bridge subjected to vessel collision[J]. Journal of Vibration and Shock, 2012, 31(10):68-73.

[14]Petersen M J. Dynamics of ship collisions[J]. Ocean Engineering, 1982, 9(4): 295-329.

[15]李军,王君杰,欧碧峰. 船桥碰撞数值模拟方法研究[J]. 公路,2010(10):14-20.

LI Jun, WANG Jun-Jie, OU Bi-feng. Research on numerical simulation of ship-bridge collision[J]. Highway, 2010(10):14-20.

[16]JTG D63-2007.公路桥涵地基与基础设计规范 [S]. 北京:人民交通出版社, 2007.

[17]同济大学土木工程防灾国家重点实验室. 南京长江第四大桥船舶撞击动力分析研究[R], 2007.

[18]Hallquist J O.LS-DYNA theory manual[M]. Livermore Software Technology Corporation, 2006.

[19]Gluver H, Olsen D. Ship collision analysis[S].Balkema: Rotterdam, 1998.

[20]T B 10002.1-2005.铁路桥涵设计基本规范 [S]. 北京:中国铁道出版社, 2005.

[21]JTG D60-2004.公路桥涵设计通用规范 [S]. 北京:人民交通出版社, 2004.

[22]Guidespecifications and commentary for vessel collision design of highway bridges[S]. Washington D. C.：American Association of State Highway and Transportation Officials, 2009.