前后向时间序列模型联合估计的时变结构模态参数辨识

2015-12-30杨武,刘莉,周思达等

振动与冲击 2015年3期

关键词：向量

第一作者杨武男，博士生，1986年生

通信作者刘莉女，教授，1964年生

前后向时间序列模型联合估计的时变结构模态参数辨识

杨武，刘莉，周思达，马志赛

(北京理工大学宇航学院飞行器动力学与控制教育部重点实验室，北京100081)

摘要：为提高时变结构模态参数辨识精度和抗噪声能力，提出一种前后向泛函向量时变自回归滑动平均(FS-VTARMA)时间序列模型联合估计的模态参数辨识方法。首先建立前后向FS-VTARMA模型联合估计的均方误差形式的费用函数，其次引入非平稳信号中前向模型和后向模型估计系数的近似共轭关系，再利用两步最小二乘法(2SLS)得到时变模型系数，最后把时变模型特征方程转换为广义特征值问题提取出模态参数。利用时变刚度系统非平稳振动信号验证该方法，结果表明：能有效地克服前向模型估计中模态参数一步延迟以及起始时刻无法准确获得，以及后向模型估计中模态参数一步超前以及终止时刻无法准确获得的缺点，具有更高的模态参数辨识精度和更强的抗噪声能力。

关键词：时变结构；模态参数辨识；前后向时间序列；向量；泛函

收稿日期：2013-10-09修改稿收到日期：2014-03-02

中图分类号:V414；N945.14文献标志码：A

Modal parameter identification of time-varying structures using a forward-backward time series model based on joint estimation

YANGWu,LIULi,ZHOUSi-da,MAZhi-sai(MOE Key Laboratory of Dynamics and Control of Flight Vechile, School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

Abstract:To improve modal parameter identification precision and anti-noise performance for time-varying structures an identification approach using a forward-backward functional series vector time-dependent ARMA time series model (FS-VTARMA) based on joint estimation was presented. Firstly, a cost function in the form of mean square error for joint forward-backward estimation of FS-VTARMA model was established. Secondly, the estimated parameters of forward and backward models for a non-stationary signal were approximately complex conjugate. Then, the time-varying model coefficients were obtained using the two-stage least square (2SLS) method. Finally, its modal parameters were extracted from a generalized eigenvalue problem transformed from an eigenvalue equation of the time-varying model. The identification approach was validated with non-stationary vibration signals of a system with time-varying stiffness. The results indicated that the proposed method can not only overcome shortages of one-step delay and initial prediction error in the forward model’s modal parameter estimation, but also overcome shortages of one-step step lead and terminal prediction error in the backward model’s modal parameter estimation, it has higher modal parameter identification precision and better anti-noise performance.

Key words:time-varying structures; modal parameter identification; forward-backward time series; vector; functional series

工程实际中，工作中的机械臂、车辆通行中的桥梁、发射中的运载火箭、帆板展开中的航天器等结构都存在随时间变化的动力学特性。由于这些结构常常在工作中才表现出时变动力学特性且所作用的激励力未知或随机，因此采用工作模态分析(仅输出模态分析，OMA)来辨识模态参数。

现有时变结构模态参数辨识按照辨识域分为频域和时域。时域辨识方法主要分为随机子空间法[1]和时间序列法。其中时间序列法近80年以来得到长足发展，已经从时不变结构拓展到时变结构。最近参数化时域模态参数辨识是一个热点问题[2-3]。为提高辨识精度和抗噪声能力，Sodsri[4]把运用在平稳信号中的前后向线性预测(FBLP)[5]扩展到非平稳信号，提出一种前后向泛函时变自回归(FS-TAR)模型联合估计的瞬时频率辨识方法。芦玉华等[6]在对滚动轴承故障诊断中运用前后向FS-TAR模型联合估计方法，采用递推最小二乘(RLS)技术提取出特征频率。Kazlauskas等[7]运用前后向FS-TAR模型联合估计方法辨识噪声环境中调制信号的瞬时频率。同时，为让模型参数简约，且能辨识工作参考向量和反共振点，Spiridonakos等[8]提出泛函向量时变自回归滑动平均(FS-VTARMA)模型，但是该模型是一种前向模型，对辨识的模态参数产生一步延迟，且无法准确地获得起始时刻的模态参数。

本文结合FS-VTARMA模型和前后向FS-TAR模型各自的优点，提出一种模型参数简约、辨识精确、抗噪声强、能辨识工作参考向量和反共振点的前后向泛函向量时变自回归滑动平均模型(FS-VTARMA)联合估计的模态参数辨识方法。首先建立前后向FS-VTARMA模型联合估计的均方误差形式的费用函数，再根据非平稳信号中前向模型和后向模型估计系数的近似共轭关系，利用两步最小二乘方法得到时变模型系数，最后把时变模型特征方程转换为广义特征值问题提取出模态参数。利用时变刚度系统非平稳振动信号对该辨识方法的有效性进行验证。

1前向和后向FS-VTARMA模型的建立

(1)

(2)

其中:t为离散时间，上标“f”和“b”分别为前向和后向估计标识符，x[t]k×1为非平稳复时间序列，w[t]k×1为满足零均值和协方差Σ[t]k×k的不相关复残差序列，p和q分别为自回归(AR)和滑动平均(MA)阶数，且满足p≥q，而Ai[t]k×k和Ci[t]k×k分别为相应的复时变系数。把Ai[t]、Ci[t]和Σ[t]分别在函数子空间

(3)

上展开，得到泛函向量时变自回归滑动平均模型FS-VTARMA(p,q,k)[l,m,n]，其中，l、m和n分别为子空间Υ、Γ和Ψ的维度，而下标ar(i)(i=1,…,l)，ma(i)(i=1,…,m)，co(i)(i=1,…,n)为对应子空间的基函数标识。该基函数可以从任何函数族(如三角函数、切比雪夫、勒让德等)中选择。而Ai[t]、Ci[t]和Σ[t]在函数子空间上展开形式为：

(4)

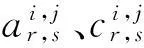
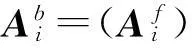
⟺Af[R,t]·x[t]=Cf[R,t]·wf[t]

⟺Gf[R,t]·x[t]=wf[t]

(5)

⟺(Af[L,t])*·x[t]=(Cf[L,t])*·wb[t]

⟺(Gf[L,t])*·x[t]=wb[t]

(6)

其中:定义多项式算子矩阵

Gf[R,t]≜(Cf[R,t])-1。Af[R,t]=

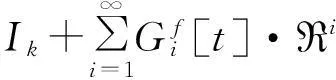
(Gf[L,t])*≜((Cf[L,t])*)-1。(Af[L,t])*=

(7)

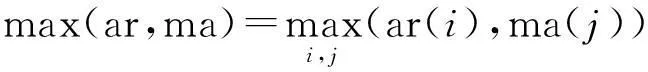
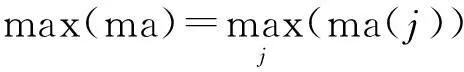
2前后向模型联合估计

根据参数估计原理[13]，建立前后向模型联合估计的费用函数，再最小化费用函数得待估参数。

2.1联合估计的费用函数

把前向和后向模型的残差序列均方误差(MSE)求和，得到联合估计的费用函数为

(8)

一般地，含MA的费用函数，估计参数θ是一个非线性优化过程，十分耗时且可能为局部最优。需要把该过程转化为线性求解过程，主要方法包括[12]：多项式-代数法(P-A)、递推扩展最小二乘法(RELS)和两步最小二乘法(2SLS)。P-A法精度高但耗时；RELS法精度不高；2SLS法精度较高且计算效率高。

2.2AR和MA时变系数矩阵估计

2SLS法的基本思想为利用逆函数把FS-VTARMA模型转化成两个可以线性求解的FS-VTAR模型：第一步对FS-VTARMA模型相等价的无限阶时变FS-VTAR逆函数模型进行o阶截断，求出该模型的残差序列值；第二步利用该残差序列值把原FS-VTARMA模型转换成一个MA已知的可线性求解的FS-VTAR模型。

2.2.1第一步：逆函数估计

对式(5)中Gf[R,t]取o阶截断得逆函数模型为

t=1～N-o

(10)

其中:

。

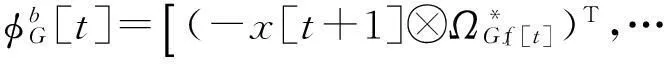
利用wb[t,g]和wb[t,g])*不会改变费用函数值的特性，得前后向逆函数模型联合估计的费用函数为

(11)

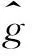
(12)

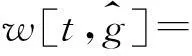
(13)

2.2.2第二步：AR和MA系数估计

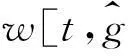
其中:

Φf[t]=φf[t]⊗Ik,

φf[t]=[(-x[t-1]⊗Υar[t])T,…,

(-x[t-p]⊗Υar[t])T,

Υar[t]=[Υar(1)[t],…,Υar(l)[t]]T,

Γma[t]=[Γma(1)[t],…,Γma(m)[t]]T

同理，后向模型转化为一个后向的线性估计过程为，

x[t]=(Φb[t])T·θ*+wb[t,θ],

t=1～N-p

(15)

其中:

Φb[t]=φb[t]⊗Ik,

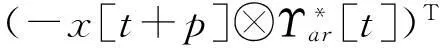
(16)

2.3协方差时变系数矩阵投影系数估计

(18)

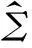
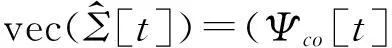
(19)

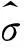
3模型结构选择

模型结构选择基本过程为：根据经验和信号变化特性，选择一个恰当的函数族，再对信号进行分析，确定FS-VTARMA(p,q,k)[l,m,n]模型参数p，q，l，m，n，ar(i)，ma(i)和co(i)的值。函数族类型的选择没有一个固定准则，只要函数空间维度足够大，任何变化形式的模型都可以得到很好近似。模型结构的确定分解为两个子问题：①模型阶数(p,q)选择；②函数子空间(l,m,n,ar(i),ma(i),co(i))选择。

3.1模型阶数(p,q)选择

目前确定模型阶数的准则很多，包括AIC、BIC和FPE等[10]，本文采用向量模型的BIC准则[14]，

(w[t,θ])H·(∑(t,σ))-1·w[t,θ])+

(20)

其中:d为模型独立估计参数个数k·k·(p·l+q·m+n)。

3.2函数子空间(l,m,n,ar(i),ma(i),co(i))选择

考虑到(ar(i),ma(i),co(i))才是独立变量，若以“1”表示存在，“0”表示不存在，从而可以把函数子空间的选择问题转换为求BIC最小的离散变量优化问题。

4时变模态参数估计

4.1“时间冻结”的功率谱密度函数

其中:ω为圆频率，Ts为采样周期，j为虚数单位。

4.2“时间冻结”的模态参数

在t时刻“时间冻结”，取R=z-1(z变量)，得到离散系统特征多项式为

(22)

为了避免求解非线性方程组，该多项式的根可以转换为一个广义特征值问题[15]，

(D-λrI)·Vr=0

(23)

其中:λr为特征根(r=1,…,k·p)，系统特征矩阵

特征向量

Lr为工作参考向量。相应的，连续系统的模态频率和模态阻尼比为

fr[t]=2π|lnλr[t]|/Ts

ζr[t]=-Re(λr[t])/|lnλr[t]|

(24)

5精度与抗噪声测试

选择三角余弦函数族：

(25)

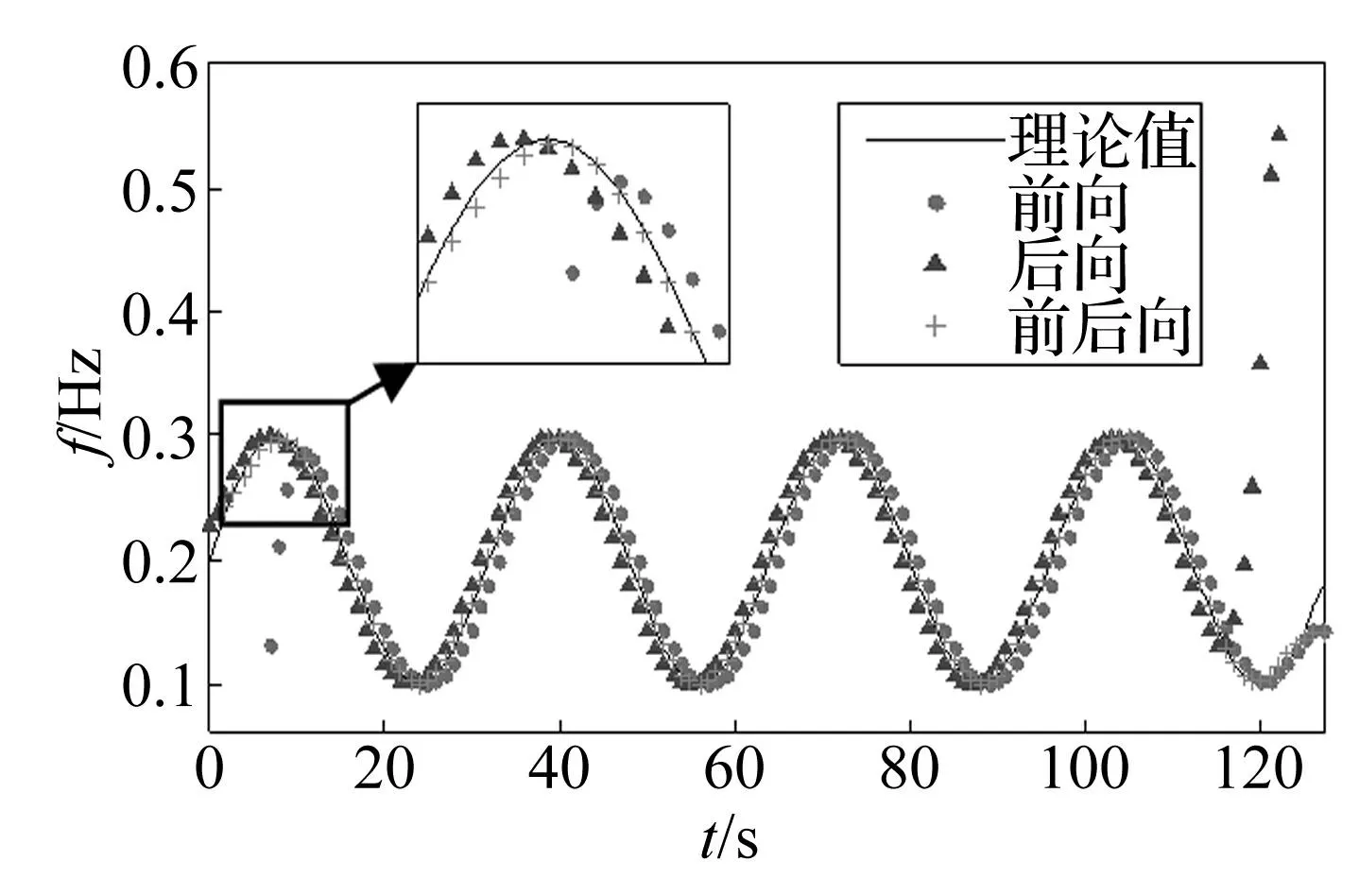
图1　无噪声周期变化正弦信号模态频率辨识结果对比 Fig.1 Comparation with modal frequency identification of the noise-free sine signal

图2　含噪声周期变化正弦信号模态频率辨识结果对比 Fig.2 Comparation with modal frequency identification of the noisy sine signal

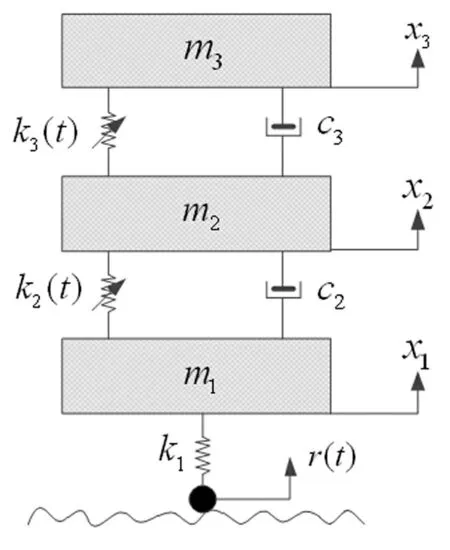
图3　时变刚度系统 Fig.3 A system with time-varying stiffnesses

由图1可知，前向估计中模态频率一步延迟，且在起始时刻出现很大的偏差；后向估计中模态频率一步超前，且在在终止时刻出现很大的偏差；然而前后向联合估计中模态参数在起始时刻和终止时刻均有很好的估计精度。由图2可知，加入噪声后，前向估计和后向估计中模态频率精度均降低，而前后向联合估计具有一定的抗噪声能力，模态参数精度依然较高。

表1　估计误差对比

由表1可知，噪声会导致估计误差的增加，而前后向联合估计误差比前向和后向均小，抗噪能力强。

6非平稳振动下时变刚度系统模态参数辨识

以时变刚度系统非平稳振动[12](如图3所示)对前后向FS-VTARMA模型联合估计模态参数辨识方法进行验证。

该时变系统的运动学方程为

(26)

其中:x(t)为位移响应，r(t)为白噪声随机激励，

ki(t)=ki,0+ki,1·sin(2πt/Pi,1)+ki,2·sin(2πt/Pi,2),(i=2,3)。系统的各个参数值如表2所示。

表2　时变系统参数

为消除初始影响取t=[-16.67,850]s，采用变积分步长龙格-库塔法对时变系统的运动学方程式(26)求解，再进行48 Hz重采样、6 Hz滤波和12 Hz重采样，最后取t=[0,850]s(N=10 200)为分析信号。利用Monte Carlo分析，产生50组白噪声激励，重复以上过程，生成50组分析信号，该信号不含测量噪声。

时变刚度系数以正弦变化，故选择三角函数族：

其中:n为基函数阶数，t=1,…,N。选择逆函数模型的截断阶数o=20，滑动时间窗长度L=256。确定前向、后向和前后向估计的初始模型都为FS-VTARMA(6,6,3)[50,10,40]，以前向估计为例(随机选择一个分析信号)，以BIC为准则的模型阶数选择过程如图4所示。

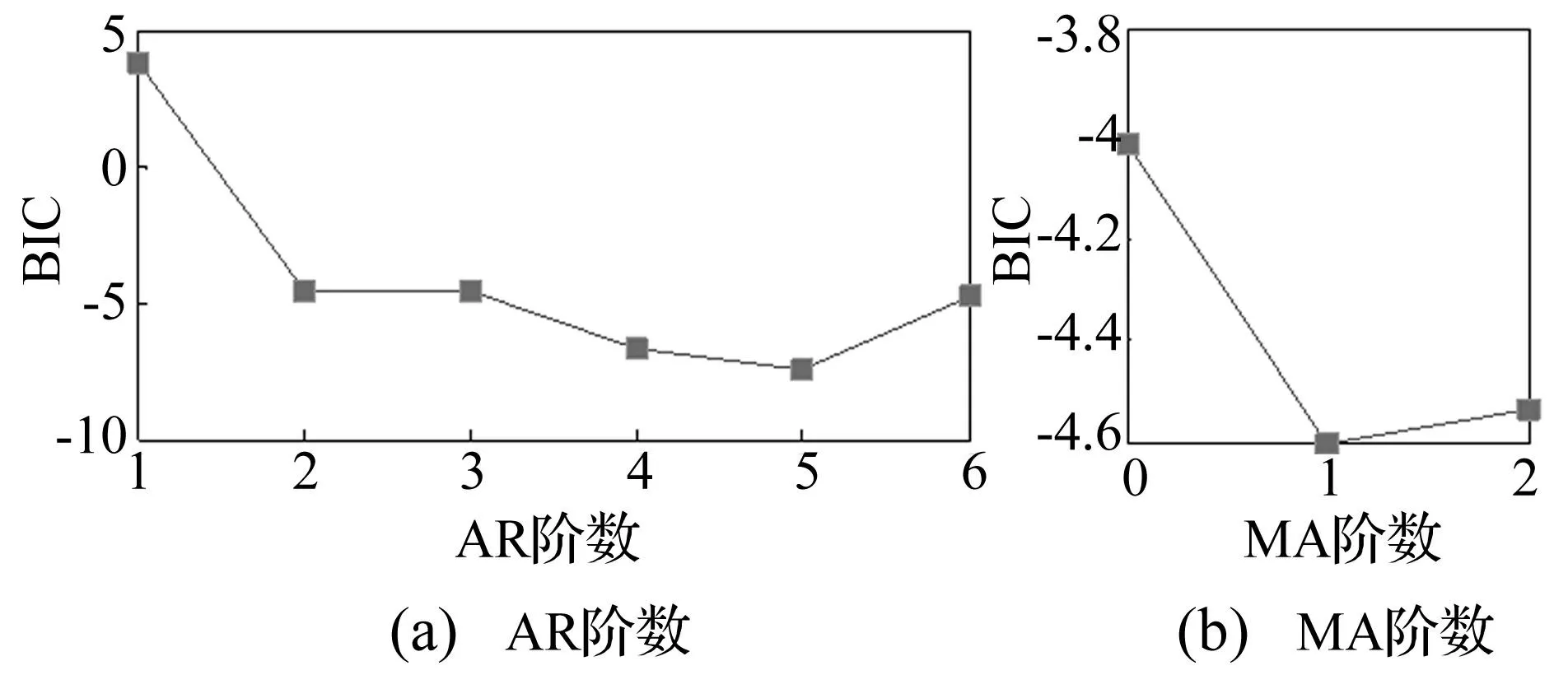
图4　前向估计模型阶数选择 Fig.4 Modal order selection for forward estimation

由图4可知，AR阶数从p=2，MA阶数从q=1开始趋于平缓。确定出前向估计的模型阶数为(2,1)，同理，确定出前向估计和前后向估计的模型阶数均为(2,1)。利用遗传算法(GA)，基函数子空间优化得到：

前向FS-VTARMA(2,1,3)[35,6,15]、后向FS-VTARMA(2,1,3)[37,4,14]和前后向FS-VTARMA(2,1,3)[28,4,8]。

利用所确定的模型结构，对50组信号分别进行模态参数辨识，前向、后向和前后向辨识的模态频率分别如图5、6和7所示(图中“○”为“时间冻结”理论值)，估计误差E(50组均值/方差)如表3所示。

由图5～7可知：在起始时刻和终止时刻，少数组分析信号对第2和3阶模态的前向和后向估计误差都较大，这是由于白噪声激励的随机性影响模态参数辨识精度；而前后向估计在整个时段中受白噪声激励随机性影响小、鲁棒性好。

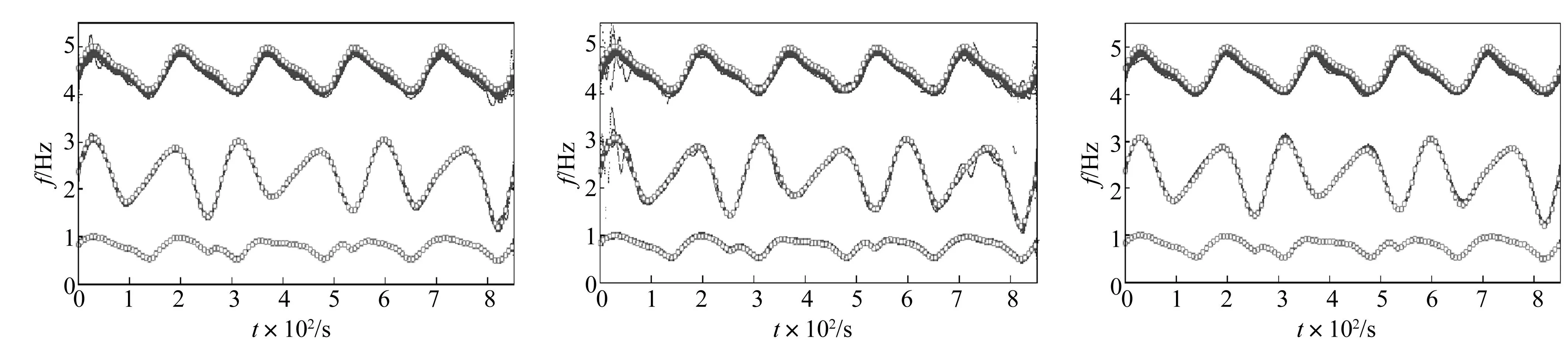
图5 前向模型估计模态频率值Fig.5Modalfrequenciesofforwardmodelestimation图6 后向模型估计模态频率值Fig.6Modalfrequenciesofbackwardmodelestimation图7 前后向模型估计模态频率值Fig.7Modalfrequenciesofforward-backwardmodelestimation

表3　估计误差均值和方差对比

由表3可知，三种估计方法对第1阶模态的估计误差均值近似相等，前后向联合估计对第2和3阶模态的误差均值比前向和后向估计误差均值略大，这是由于前向估计中模态频率一步延迟和后向估计中模态频率一步超前与采样频率相关，随着采样频率的增加，延迟和超前值减小[4]。本算例中采样频率相对较高，故三者的误差值相近。三阶模态中前后向联合估计的方差均最小，受白噪声激励随机性影响小。

为了研究噪声对前后向联合估计的影响，分别在50组无噪声信号中加入SNR为30 dB和20 dB的白噪声，选择与无噪声相同的模型结构参数值，分别进行模态参数辨识，估计误差E如表4所示。

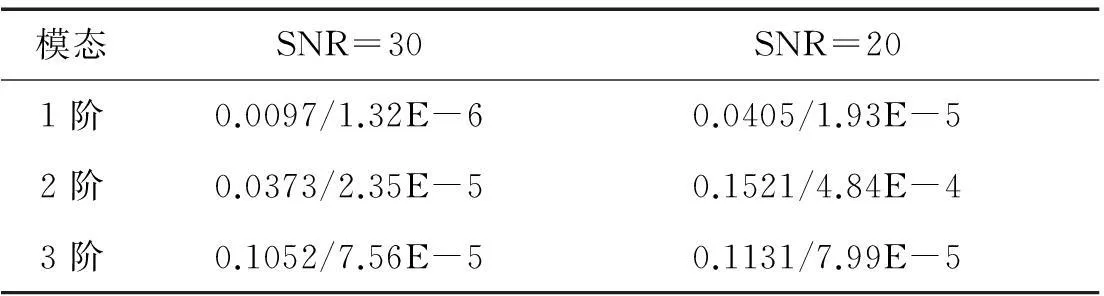
表4　含噪声估计误差均值/方差对比

由表4可知，加入噪声后前后向估计误差的均值和方差较无噪声情况有较小增加，估计结果受测量噪声激励影响小且鲁棒性好。

7结论

针对时变结构模态参数辨识中辨识精度和抗噪声问题，提出一种前后向泛函向量时变自回归滑动平均模型联合估计的模态参数辨识方法。通过频率周期变化的实正弦信号和时变刚度系统非平稳振动信号对该方法进行验证，结果表明：能有效地消除前向估计中模态参数一步延迟以及起始时刻无法准确获得，后向估计中模态参数一步超前以及终止时刻无法准确获得的缺点；具有更高的模态参数辨识精度和更强的抗噪声能力。该方法可以进一步应用于工作参考向量和反共振点的辨识。

参考文献

[1]庞世伟, 于开平, 邹经湘. 用于时变结构模态参数识别的投影估计递推子空间方法[J]. 工程力学,2005, 22(5): 115-119.

PANG Shi-wei, YU Kai-ping, ZOU Jing-xiang. A projection approximation recursive subspace method for identification of modal parameters of time-varying structures[J]. Engineering Mechanics,2005, 22(5): 115-119.

[2]续秀忠, 张志谊, 华宏星,等. 应用时变参数建模方法辨识时变模态参数[J]. 航空学报, 2003, 24(3): 230-233.

XU Xiu-zhong, ZHANG Zhi-yi, HUA Hong-xing, et al. Identification of time-variant modal parameters by a time-varying parametric approach[J], Acta Aeronautica Et Astronautica Sinica, 2003, 24(3): 230-233.秀忠, 张志谊, 华宏星,等. 应用时变参数建模方法辨识时变模态参数[J]. 航空学报, 2003, 24(3): 230-233.

[3]Spiridonakos M D, Fassois S D. Non-stationary random vibration modelling and analysis via functional series time-dependent ARMA (FS-TARMA) models-A critical survey[J]. Mechanical Systems and Signal Processing,2014. (Article in Press)

[4]Sodsri C. Time-varying autoregressive modelling for nonstationary acoustic signal and its frequency analysis[D]. Pennsylvania State University, 2003.

[5]Ulrych T J,Clayton R W. Time series modeling and maximum entropy[J]. Phys. Earth. Planet. Inter,1976, 12(2-3):188-200.

[6]芦玉华,王仲生,姜洪开. 基于改进时变自回归模型的滚动轴承故障诊断[J]. 振动与冲击,2011,30(12):74-77.

LU Yu-hua, WANG Zhong-sheng, JIANG Hong-kai. Fault diagnosis of rolling bearings based on an improved time-varying autoregressive model[J]. Journal of Vibration and Shock, 2011,30(12):74-77.玉华,王仲生,姜洪开. 基于改进时变自回归模型的滚动轴承故障诊断[J]. 振动与冲击,2011,30(12):74-77.

LU Yu-hua, WANG Zhong-sheng, JIANG Hong-kai. Fault diagnosis of rolling bearings based on an improved time-varying autoregressive model[J]. Journal of Vibration and Shock, 2011,30(12):74-77.

[7]Kazlauskas K, Pupeikis R. A forward-backward approach for instantaneous frequency estimation of frequency modulated signals in noisy environment[J]. Informatica, 2012, 23(1): 65-76.

[8]Spiridonakos M D, Fassois S D. Parametric identification of a time-varying structure based on vector vibration response measurements[J]. Mechanical Systems and Signal Processing,2009, 23(6): 2029-2048.

[9]Marple S L. Digitalspectral analysis with applicaion[M]. New York: Prentice-Hall PTR,1987.

[10]Kamen E. The poles and zeros of a linear time-varying system[J]. Linear Algebra and its applications,1988, 98(1): 263-289.

[11]Ghosh B, Bouthellier P. Simultaneous coefficient assignment of discrete time multi-input multi-output linear time-varying system: a new approach for compensator design[J]. SIMA Journal on Control and Optimization,1993, 31(6): 1438-1461.

[12]Poulimenos A G, Fassois S D. Parametric time-domain methods for non-stationary random vibration modelling and analysis-A critical survey and comparison [J]. Mechanical Systems and Signal Processing,2006, 20(4): 763-816.

[13]Ljung L. System identification: Theory for the user, second edition[M]. New Jersey: Prentice-Hall PTR,1999.

[14]Reinsel G. Elements of multivariate time seriesanalysis[M]. Berlin: Springer,1993.

[15]HeylenW, Lammens S, Sas P. Modal analysis theory and testing[M]. Belgium: Katholieke Universiteit Leuven, 2007.世伟, 于开平, 邹经湘. 用于时变结构模态参数识别的投影估计递推子空间方法[J]. 工程力学,2005, 22(5): 115-119.