考虑微穿孔管消声器结构参数的共振频率预估模型

第一作者左曙光男，博士，教授，博士生导师，1968年生

考虑微穿孔管消声器结构参数的共振频率预估模型

左曙光，龙国，吴旭东，相龙洋，张孟浩，胡佳杰(同济大学 新能源汽车工程中心，上海201804)

摘要：引入微穿孔板声阻抗理论模型，通过微穿孔管消声器传声损失测试验证基于该模型的传声损失数值计算方法的正确性。利用数值方法计算微穿孔管消声器传声损失获得共振频率。单因素法分析穿孔段长度、穿孔率、穿孔直径和空气腔厚度等结构参数变化对共振频率影响发现，穿孔段长度及空气腔厚度对共振频率影响显著。利用均匀设计结合回归分析法所得共振频率预估模型，能直接反映微穿孔管消声器共振频率与结构参数之关系，对微穿孔管消声器优化设计具有指导意义。

关键词：微穿孔管消声器；声阻抗模型；共振频率；单因素分析；预估模型

基金项目：国家重大仪器设备专项(2012YQ150256)

收稿日期：2014-02-26修改稿收到日期：2014-04-24

中图分类号:TB535文献标志码：A

Resonant frequency predicting model for a micro-perforated tube muffler considering its structural parameters

ZUOShu-guang,LONGGuo,WUXu-dong,XIANGLong-yang,ZHANGMeng-hao,HUJia-jie(Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China)

Abstract:The resonant frequency of a micro-perforated tube muffler (MPTM) is closely related to its parameters, such as, perforation segment length, perforation rate, perforation diameter and air-cavity thickness etc. Here, a theoretical acoustic impedance model of a mirco-perrorated plate (MPP) was introduced firstly and a measurement for transmission loss (TL) of a micro-perforated tube muffler was conducted to validate the correctness of the TL numerical calculation method based on the model introduced above. Then the MPTM’s resonant frequency was obtained from the TL results calculated with the numerical calculation method. The effects of the MPTM’s structural parameters on its resonant frequency were analyzed with the single factor analysis method. The results showed that perforation segment length and air-cavity thickness have significant effects on a MPTM’s resonant frequency. Moreover, a resonant frequency predicting model for a MPTM was derived with the uniform design method and the regression analysis, it could reflect directly the relationship between a MPTM’s resonant frequency and its structural parameters. The predicting model provided a guide for the optimal design of MPTMs.

Key words:micro-perforated tube muffler (MPTM); acoustic impedance model; resonant frequency; single factor analysis; predicting model

微穿孔管消声器为基于微穿孔板吸声理论[1]用于管道消声的共振式消声器。由穿孔管及其外部空气腔组成的腔体类似多个亥姆霍兹共振器并联，具有良好的宽频消声效果[2-3]。声波在微穿孔管消声器内激起共振时声能损耗最大，消声效果最显著。由于微穿孔管消声器共振频率附近消声带较窄，共振峰偏移易导致消声量急剧下降，准确确定共振频率至关重要。马大猷最先分析获得微穿孔板吸声结构的共振频率，但该隐式复杂表达式不能直接求值。而微穿孔板吸声结构共振频率亦不能反映集阻抗复合消声特性于一体的微穿孔管消声器共振频率。Selamet等[4]利用二维分析方法建立穿孔管消声器传声损失的理论模型获得共振频率，并定性分析消声器参数对共振频率影响。高林[5]利用有限元数值仿真计算亥姆霍兹共振式消声器共振频率，发现与实验存在一定误差并分析误差产生原因。毕嵘[6]将集中参数法、理论及数值仿真法所得亥姆霍兹共振式消声器共振频率与实验结果对比发现，数值计算结果更接近实验值，相对误差约3%。孟新等[7]通过求解亥姆霍兹共振消声器的气流再生噪声获得共振频率，但缺少实验证明。罗虹等[8-9]利用有限元方法计算穿孔管消声器的传声损失并分析归纳穿孔管结构参数对共振频率影响。由此可见，共振式消声器共振频率求解大多基于颈部直径较大的单腔亥姆霍兹共振器模型，利用集中参数法或理论方法，所求结果与实验结果偏差较大，数值方法则更繁琐。而针对微穿孔管消声器共振频率研究极少，仍未获得较准确反映共振频率与结构参数关系计算式。

本文用数值计算方法求解微穿孔管消声器传声损失获得共振频率，分析主要结构参数对共振频率影响。引入微穿孔板声阻抗理论模型，通过实验验证基于该模型的微穿孔管消声器传声损失数值计算方法。通过单因素法分析结构参数对共振频率影响。基于均匀设计结合回归分析方法获得微穿孔管消声器共振频率预估模型。

1微穿孔板声阻抗理论模型

图1为考虑中低声强下基于短管(管长远小于声波长)的声传播模型，其短管声阻抗[10]为

(1)

(2)

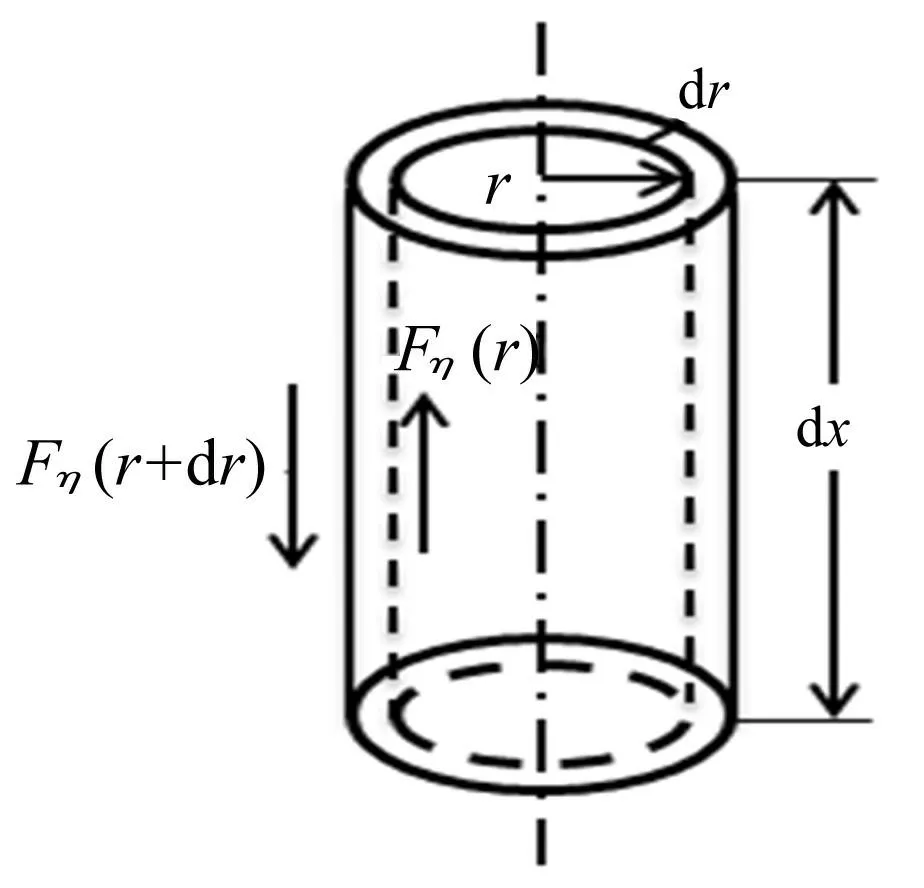
图1　考虑管壁粘滞作用的 短管内媒质运动模型 Fig.1 Model of medium motion in short tube considering viscous effect

式中：j为虚数单位；ω为声波波动圆频率；ρ为流体介质密度；t为短管长度；d为短管直径；J0，J1分别为0、1阶第一类贝塞尔函数；η为流体切变粘滞系数。

当管长t不比管径d大的多时，需加末端修正值[11]，则修正后的短管声阻抗为

(3)

式中：Δl0为末端修正等效长度，即

Δl0=0.85d

(4)

考虑微穿孔板小孔间距大于孔径，忽略穿孔间相互影响。单个小孔(视为短管)声阻抗除以穿孔率及空气特性阻抗得微穿孔板相对声阻抗率为

(5)

式中：p为微穿孔板穿孔率；c为空气声速；ρc为空气特性阻抗。

式(3)～式(5)构成微穿孔板声阻抗理论模型。需指出的是，在计算机技术尚不能满足计算要求年代，文献[1]为方便制作参数设计表格，对模型中贝塞尔函数近似简化。现可借助科学软件直接计算贝塞尔函数，无需简化。

2数值计算方法的实验验证

本文研究的微穿孔管消声器各结构参数表示见图2(穿孔段长度l、空气腔厚度D、前后内插管长度l1及l2、内管管径D0分别对应图2标示；其它参数包括穿孔孔径d、穿孔层厚度t、穿孔率p)。此处简要介绍其传声损失的数值计算方法[12]。

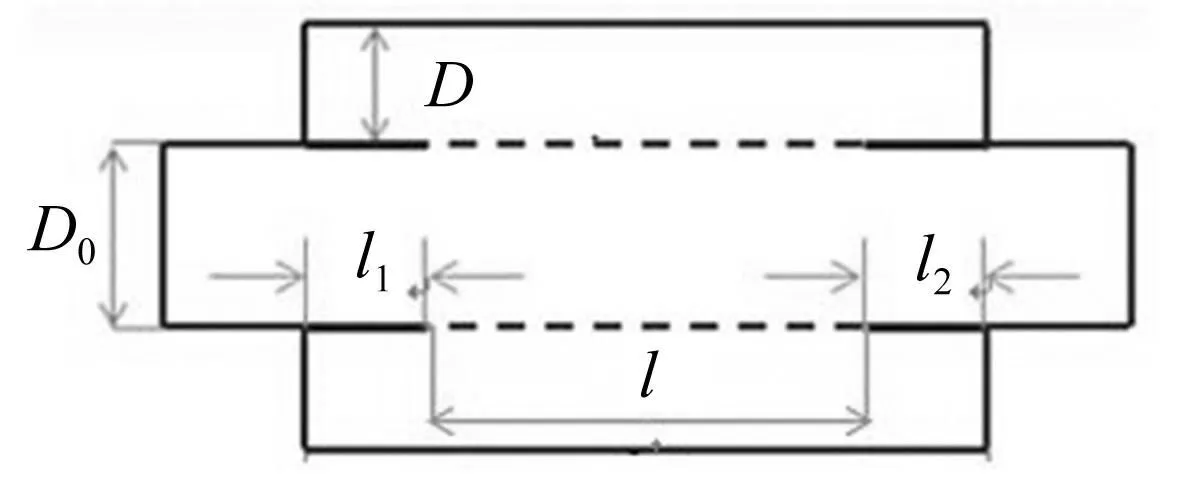
图2　微穿孔管消声器示意图 Fig.2 Schematic diagram of a micro-perforated tube muffler

利用有限元软件对微穿孔管消声器传声损失进行数值求解。有限元仿真模型见图3。实体建模时忽略消声器内部声传播过程的流固耦合作用，仅建立消声器内部空气腔模型。建模后在有限元软件中分别定义入口激励、介质属性、出口无反射边界条件、小孔传递导纳关系[13]、求解器，仿真并进行后处理获得传声损失。仿真过程不计温度、气流对声传播影响；小孔传递导纳矩阵须结合微穿孔板声阻抗理论模型编程求得。

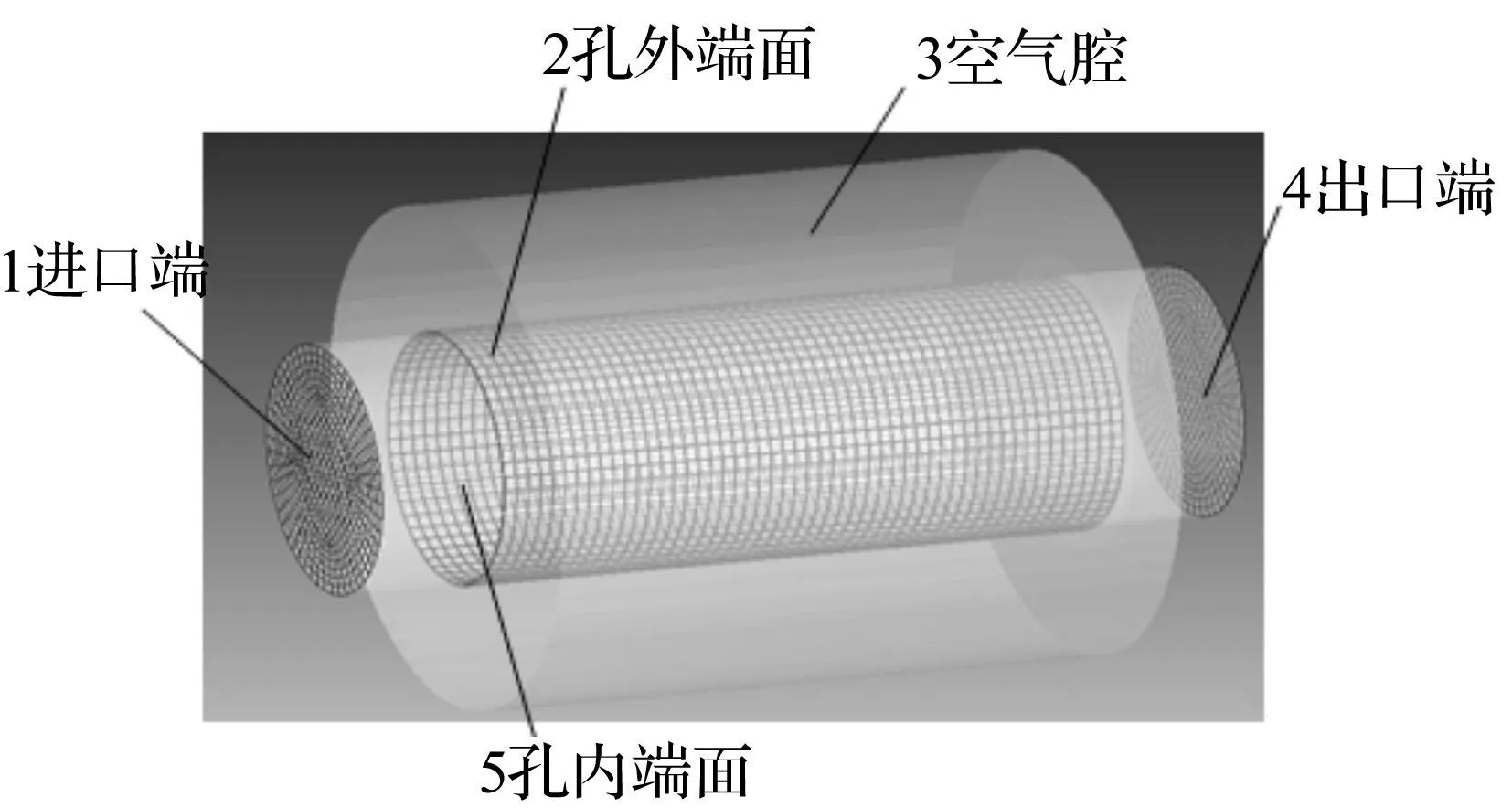
图3　微穿孔管消声器有限元模型示意图 Fig.3 Schematic diagram of a micro-perforated tube muffler FEM model

为验证基于微穿孔板声阻抗理论模型的消声器传声损失有限元数值计算方法，据双负载法[14]利用阻抗管测量消声器传声损失。实验布置见图4。所用阻抗管型号为SW466-60，传声器间距45 mm，频率测试范围400～3 150 Hz。测量样件结构参数为：D0=60 mm、D=19 mm、l=220 mm、d=0.8 mm、t=1 mm、p=2%、l1=l2=10 mm。给定声激励为白噪声信号，为忽略声阻抗非线性效应[15],实验中保证各传声器测得声压值低于100 dB。所有测量均在相同条件下重复三次，取结果平均值。将微穿孔管消声器传声损失测量结果与传声损失有限元数值计算结果对比，见图5。由图5看出，微穿孔管消声器传声损失数值计算结果与实验数据吻合较好，在消声器共振频率处基本重合(相差20 Hz，相对误差0.8%)，能较准确反映实际消声器的消声性能。故可利用该数值方法仿真计算微穿孔管消声器传声损失以确定其共振频率。

图4　微穿孔管消声器传声损失测量实验布置 Fig.4 Experimental arrangement of TL measurement

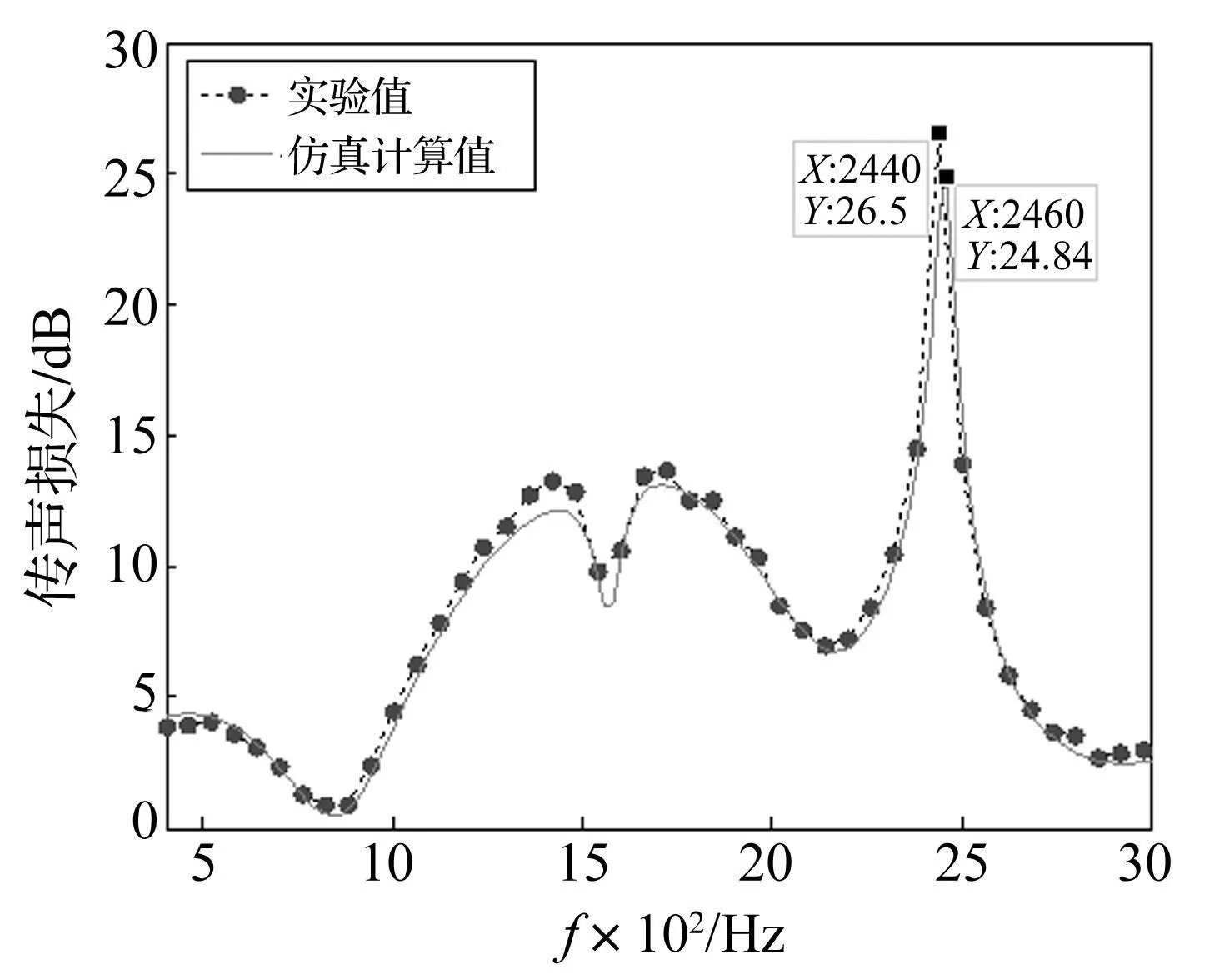
图5　微穿孔管消声器传声损失实验值与仿真值对比 Fig.5 Comparison between experiment and FEM

3微穿孔管消声器结构参数对共振频率影响分析

据文献[9]，穿孔管消声器共振频率与穿孔段长度、穿孔率、穿孔直径、空气腔厚度、穿孔层厚度等参数联系密切，需利用单因素法分析各结构参数对微穿孔管消声器共振频率影响。微穿孔管消声器共振频率即传声损失达到峰值时频率值记为fmax，见图6。

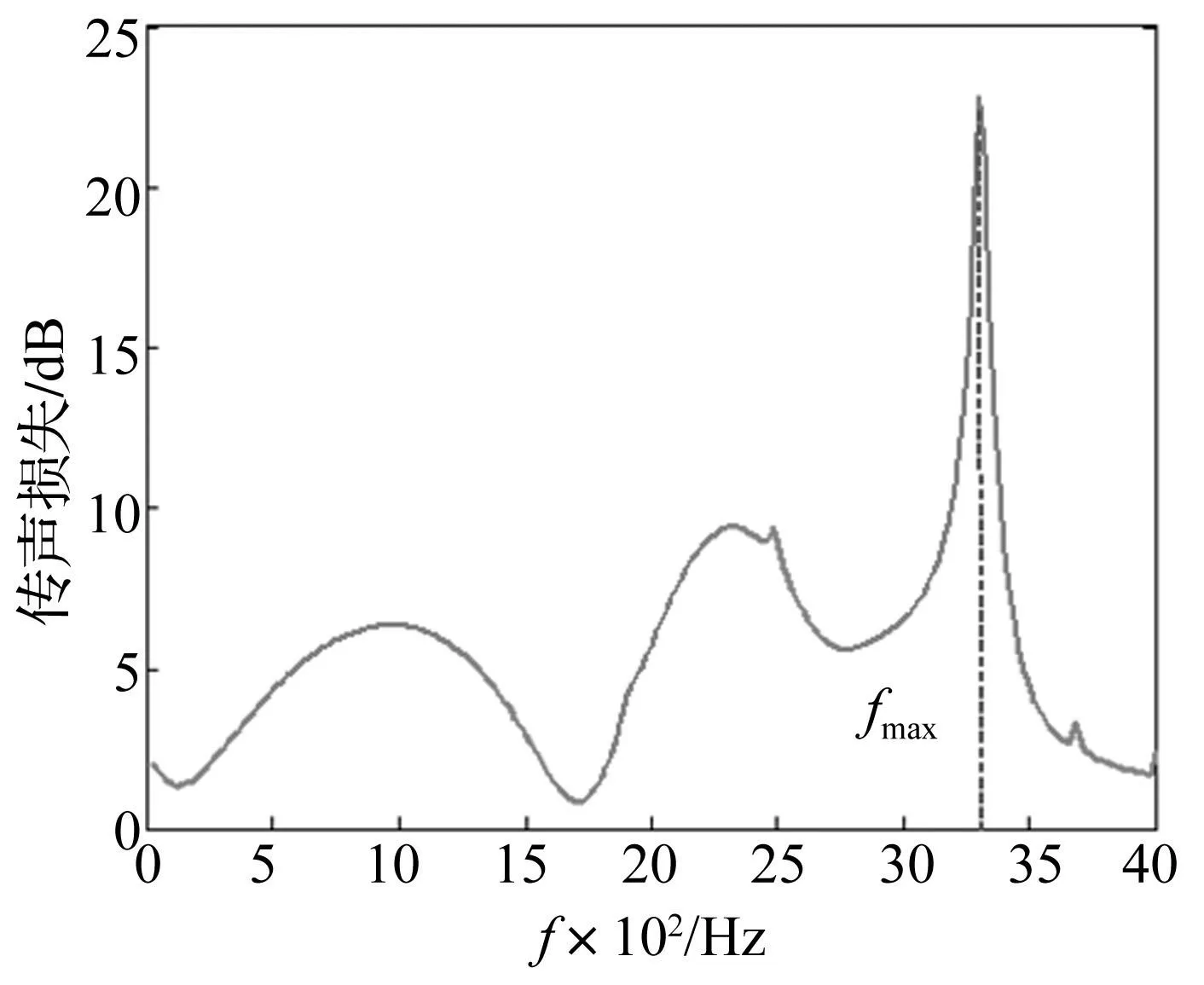
图6　某微穿孔管消声器传声损失 Fig.6 TL curve of a micro-perforated tube muffler

为简化数值建模及分析，本文不考虑内插管长度、穿孔层厚度及内管径对共振频率影响，即令仿真模型前后内插管长度l1=l2=0、穿孔层厚度t=0.5 mm、内管管径D0=50 mm保持不变，下同。仿真计算时频率步长取20 Hz。

3.1穿孔段长度对共振频率影响

令穿孔率p=2.2%、穿孔直径d=0.5 mm、空气腔厚度D=20 mm保持不变，穿孔段长度l(mm)分别取90、96、102、108、114、120，分析其变化对共振频率影响。共振频率随穿孔段长度变化趋势见图7。由图7看出，穿孔段长度由90 mm增加到120 mm时,共振频率近似线性降低且变化明显。故可通过调整微穿孔管消声器的穿孔段长度有效改变共振频率。

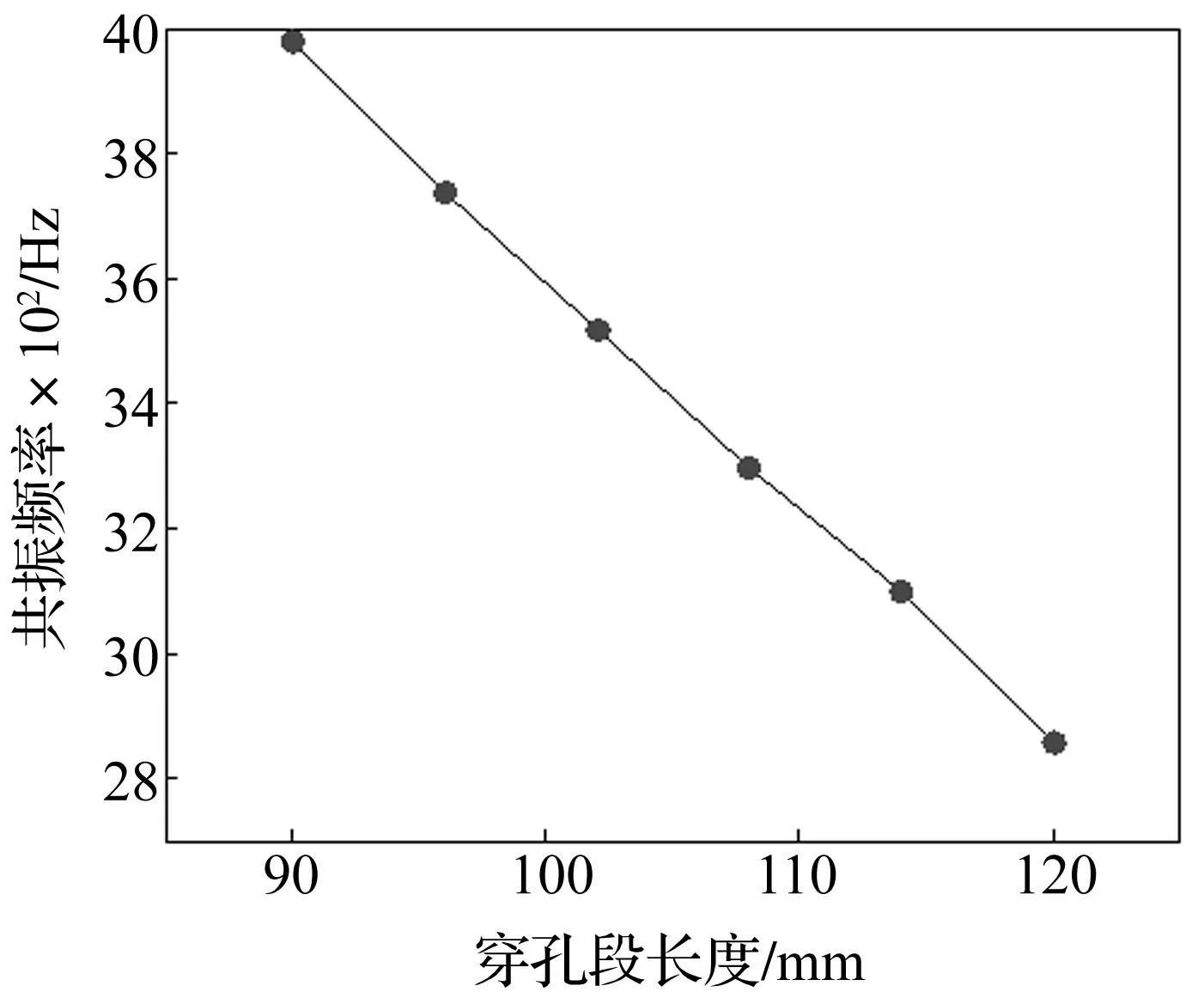
图7　不同穿孔段长度对应的共振频率 Fig.7 Resonant frequencies of micro-perforated tube mufflers with different perforation segment lengths

3.2穿孔率对共振频率影响

令穿孔段长度l=102 mm、穿孔直径d=0.5 mm、空气腔厚度D=20 mm保持不变，穿孔率p分别取1.2、1.5、1.8、2.1、2.4、2.7，分析其变化对共振频率的影响。共振频率随穿孔率变化趋势见图8。由图8看出，穿孔率由1.2%增加到2.7%时,共振频率变化较复杂，但整体变化范围较小(在40 Hz幅度变化)，可认为穿孔率在1.2%～2.7%范围变化对共振频率影响有限。考虑传统微穿孔板的穿孔率一般在3%以下，故不宜通过改变微穿孔管消声器穿孔率改变共振频率。

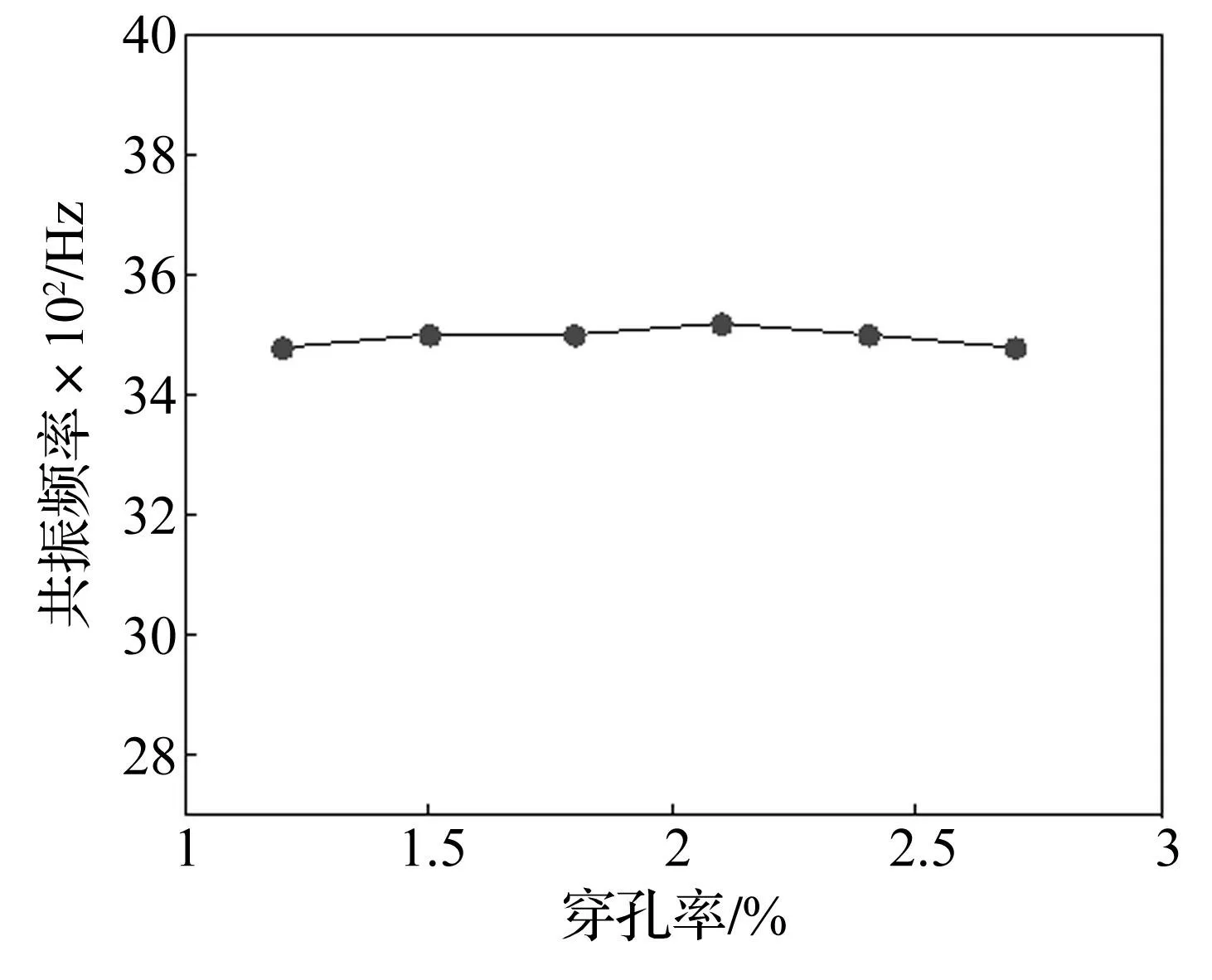
图8　不同穿孔率对应的共振频率 Fig.8 Resonant frequencies of micro-perforated tube mufflers with different perforations

3.3穿孔直径对共振频率影响

令穿孔段长度l=102 mm、穿孔率p=2.2%、空气腔厚度D=20 mm保持不变，穿孔直径d(mm)分别取0.2、0.3、0.4、0.5、0.6、0.7，分析其变化对共振频率影响。共振频率随穿孔直径变化趋势见图9。由图9看出，穿孔直径由0.2 mm增大到0.7 mm时,共振频率呈现一定波动，但幅度较小(约40 Hz)。考虑传统微穿孔板穿孔直径一般不超过1 mm，故不宜通过改变微穿孔管消声器的穿孔直径改变共振频率。

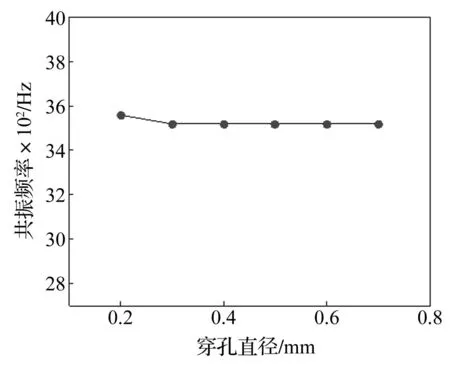
图9　不同穿孔直径对应的共振频率 Fig.9 Resonant frequencies of micro-perforated tube mufflers with different perforation diameters

3.4空气腔厚度对共振频率影响

令穿孔段长度l=102 mm、穿孔率p=2.2%、穿孔直径d=0.5 mm保持不变，空气腔厚度D(mm)分别取10、15、20、25、30、35，分析其变化对共振频率影响。共振频率随空气腔厚度变化趋势见图10。由图10看出，空气腔厚度由10 mm增加到35 mm时,共振频率逐渐降低且降幅较大，且空气腔厚度越大共振频率变化幅度越小。故当微穿孔管消声器的空气腔厚度较小时，调整其值可显著、有效改变共振频率。

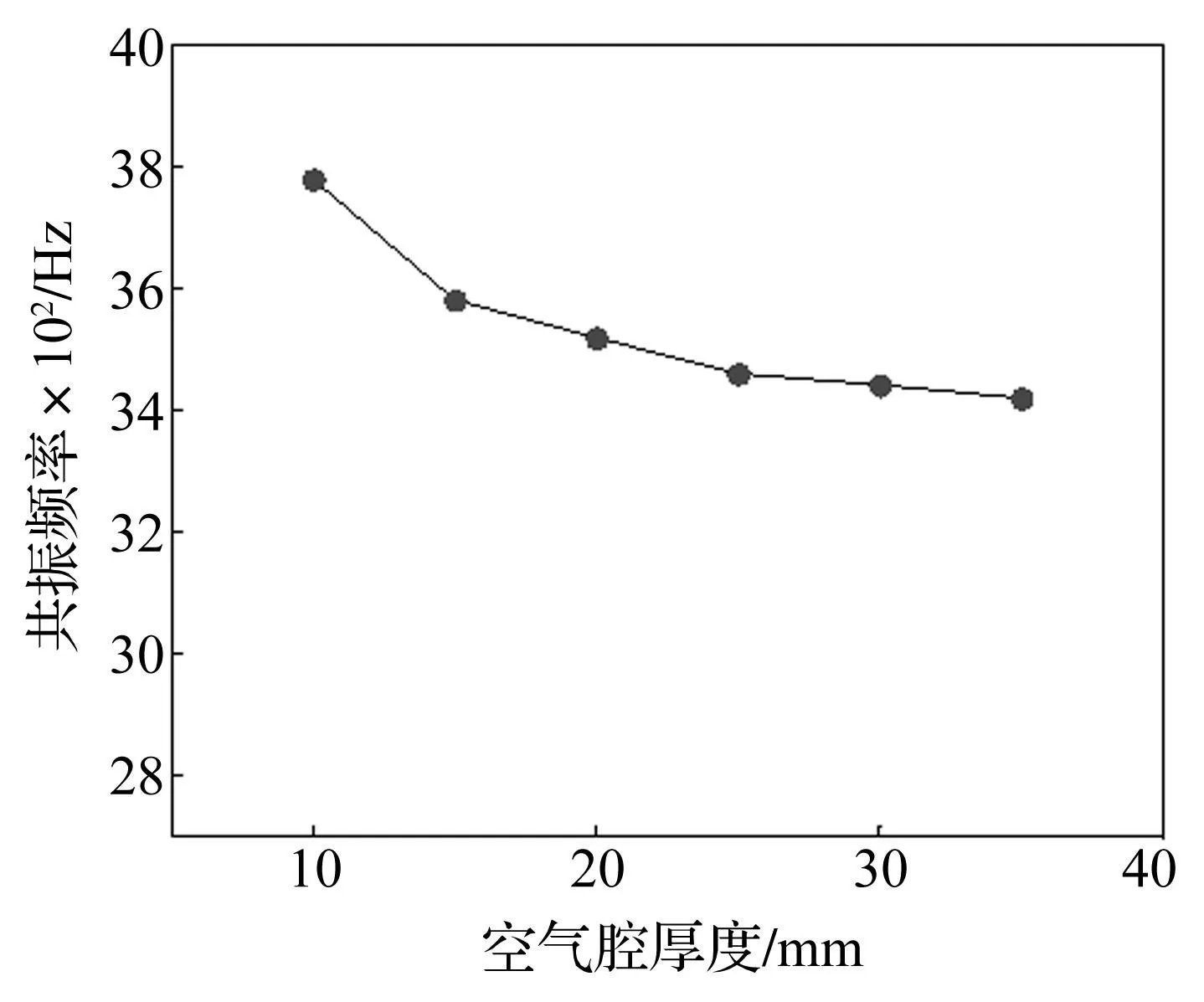
图10　不同空气腔厚度对应的共振频率 Fig.10 Resonant frequencies of micro-perforated tube mufflers with different air-cavity thickness

4微穿孔管消声器共振频率预估模型

利用均匀设计试验方法设计微穿孔管消声器的有限元数值试验模型并仿真求解传声损失，通过回归分析方法获得考虑结构参数的共振频率预估模型。

4.1均匀设计

均匀设计法[16]作为科学试验方法，将分析问题化为有同样解答的概率问题，用统计模拟方法处理。均匀设计法特点为：①试验点均匀分散，具有较好代表性；②试验次数较正交设计等试验设计方法明显减少，尤其适合多因素多水平及系统模型完全未知情况；③通过回归分析、最优化及关联度分析等方法处理试验结果能估计出模型因素的主效应与交互效应。均匀设计作为优于正交设计的新方法，已广泛应用于化工、医药、军事等行业。

表1　均匀设计试验方案

影响微穿孔管消声器共振频率的因素较多且无法确定各因素间有无交互作用。本文利用均匀设计方法，选U15(158)均匀表并结合其使用表设计了15组数值试验分别求解传声损失获得各组共振频率，见表1。微穿孔管消声器的内管管径均为50 mm，穿孔层厚度均为0.5 mm。

4.2多因素回归分析

对试验所得共振频率，见表2。用回归分析方法[17]进行处理，获得共振频率与消声器主要结构参数的回归模型。利用数学统计分析软件对表2数据进行二次多项式回归分析，所得回归方程为

fmax=379+84.6X1+5544X2-633X4-

80.5X1X2-15.8X1X3+4.61X1X4+2052X2X3+

70.9X2X4-52.1X3X4-1567X32

式中：fmax，X1，X2，X3，X4分别对应共振频率(Hz)、穿孔段长度(mm)、穿孔率(%)、穿孔直径(mm)、空气腔厚度(mm)取值。

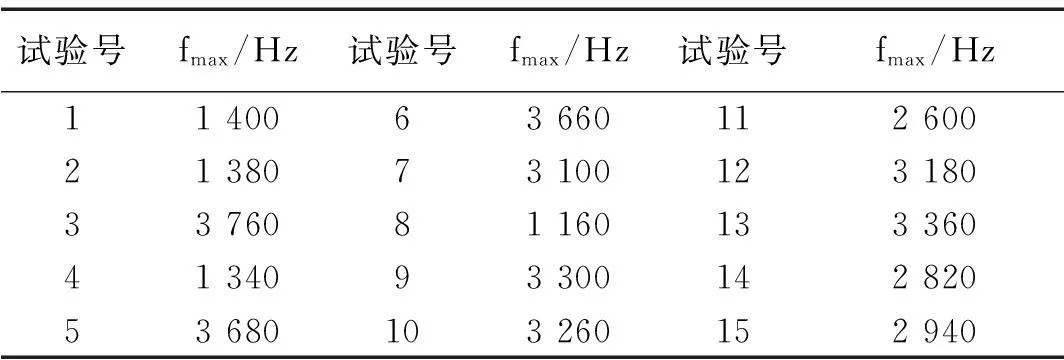
表2　试验所得共振频率f max

图11为共振频率仿真试验值与回归预估值对比。由图11可知，共振频率试验值与回归拟合值吻合良好，平均误差3.76%。所得回归模型的复相关系数R=98.7%，修正决定系数Ra=95.5%，方差分析及回归系数显著性检验分别见表3、表4。由量表看出，回归方程在α=0.01上能反映出较好的显著度及预估精度。故认为微穿孔管消声器共振频率参数回归模型满足预估要求。

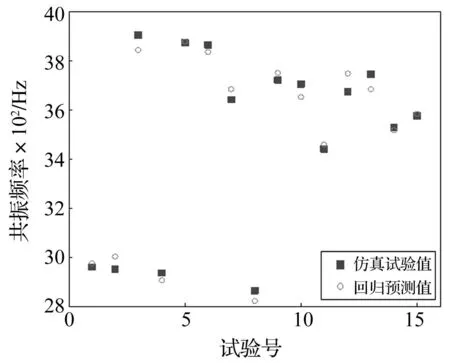
图11　共振频率的仿真试验值与回归预估值 Fig.11 Resonant frequencies calculated by FEM and prediction model

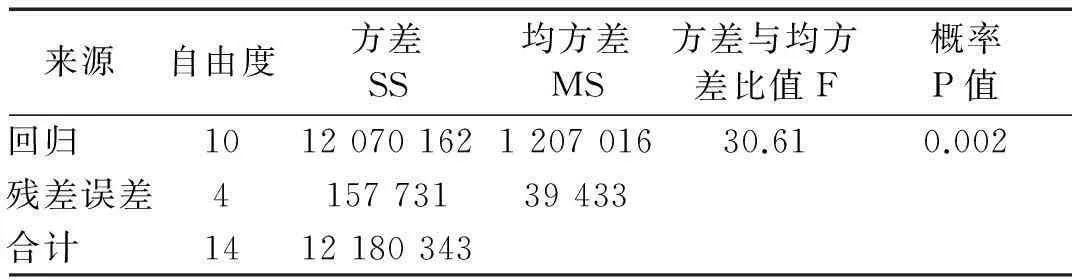
来源自由度方差SS均方差MS方差与均方差比值F概率P值回归 1012070162120701630.610.002残差误差415773139433合计 1412180343

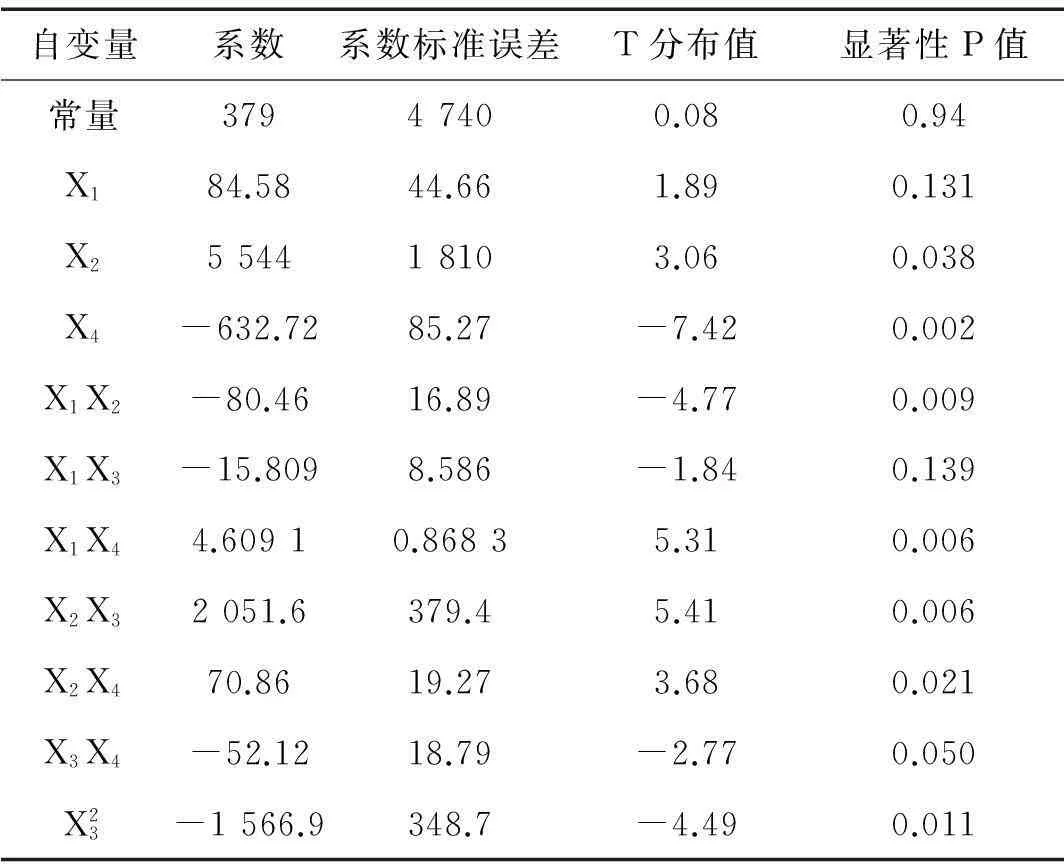
表4　回归系数的显著性检验

为进一步检验回归方程的精确度，本文另取均匀设计试验模型以外的微穿孔管消声器有限元模型并计算其传声损失获得共振频率值。计算结果及回归方程预估结果见表5。由表5知，误差不超过1%，考虑仿真计算的频率步长20 Hz会导致一定误差，故认为回归方程预估结果可以接受。

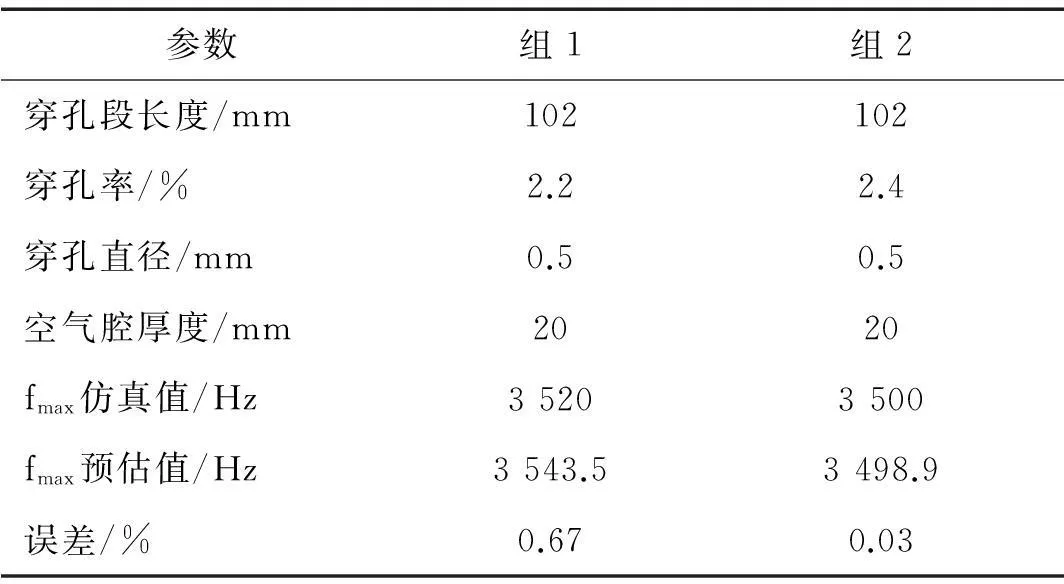
表5　共振频率回归预估值检验

在已知内管管径50 mm(受消声管路接口限制)及穿孔层厚度0.5 mm(材料限制)前提下，优化设计无内插管单层直通微穿孔管消声器，可据经验先确定微穿孔管消声器的穿孔率及穿孔直径(二者对共振频率影响相对较小)，基于共振频率预估模型，据目标消声频率及降噪量并综合考虑实际情况(消声器空间布置及加工难易等因素)，调整穿孔段长度及空气腔厚度参数即可。

5结论

本文通过分析微穿孔管消声器主要结构参数对共振频率影响，结论如下：

(1)引入较准确的微穿孔板声阻抗理论模型，并通过实验验证基于该声阻抗理论模型的消声器传声损失有限元数值计算方法。

(2)在一定范围内改变穿孔率及穿孔直径对共振频率影响不大，而改变穿孔段长度及空气腔厚度则可显著改变共振频率。增大穿孔段长度使共振频率近似线性降低；增大空气腔厚度使共振频率减小。

(3)所得考虑微穿孔管消声器结构参数的共振频率预估模型，一定程度上可指导微穿孔管消声器的优化设计。

参考文献

[1]马大猷. 微穿孔板吸声结构的理论和设计[J]. 中国科学, 1975, 18(1): 38-50.

MA Da-you. Theory and design of micro-perforated panel absorber[J]. Science China, 1975, 18(1): 38-50.

[2]阮登芳. 共振式进气消声器设计理论及其应用研究[D]. 重庆: 重庆大学, 2005.

[3]左言言,周晋花,刘海波,等. 穿孔板吸声结构的吸声性能及其应用[J]. 中国机械工程, 2007, 18(7): 778-780.

ZUO Yan-yan, ZHOU Jin-hua, LIU Hai-bo, et al. Absorption performance and application of perforated panel absorber[J]. China Mechanical Engineering,2007,18(7): 778-780.

[4]Selamet A, Xu M B, Lee I J. Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extension[J].Journal of Acoustical Society of America, 2005, 117(4): 2078-2089．

[5]高林. 多线谱可调频水消声器仿真设计研究[D]. 哈尔滨: 哈尔滨工程大学, 2011.

[6]毕嵘. 复合式消声器声学特性的分析方法和实验研究[D]. 合肥:合肥工业大学, 2012.

[7]孟新,陆森林,刘红光,等. 共振消声器共振频率的数值分析[J]. 重庆交通大学学报 (自然科学版),2012,31(5):1081-1085.

MENG Xin, LU Sen-lin, LIU Hong-guang, et al. Numerical analysis of resonant frequency of resonant muffler[J]. Journal of Chongqing Jiaotong University (Natural Science), 2012, 31(5): 1081-1085.

[8]罗虹,邓海涛,董红亮,等. 消声器共振腔及穿孔隔板消声特性数值分析[J]. 机械设计与制造, 2008 (3): 124-126.

LUO Hong, DENG Hai-tao, DONG Hong-liang, et al.Numerical analysis of mufflering characteristic for resonator and perforated clapboard in muffler[J]. Machinery Design and Manufacture, 2008 (3): 124-126.

[9]徐磊,刘正士,毕嵘. 结构参数对直通穿孔管消声器消声性能影响的数值分析[J]. 合肥工业大学学报(自然科学版), 2009, 32(11): 1637-1641.

XU Lei, LIU Zheng-shi, BI Rong. Numerical analysis of the effect of structural parameters on the acoustic attenuation performance of straight-through perforated tube silencers[J]. Journal of Hefei University of Technology(Natural Science), 2009, 32(11): 1637-1641.

[10]马大猷. 现代声学理论基础[M]. 北京: 科学出版社, 2004: 210-220.

[11]Ingard K. On the theory and design of acoustic resonators[J]. Journal of Acoust. Soc. Am, 1953, 25: 1037-1061.

[12]徐贝贝,季振林. 穿孔管阻性消声器声学特性的有限元分析[J]. 振动与冲击, 2010, 29(3): 58-62.

XU Bei-bei, JI Zhen-lin.Analysis on acoustical performance of perforated tube muffler by FEM[J]. Journal of Vibration and Shock, 2010, 29(3): 58-62.

[13]贺岩松,李景,卢会超. 组合式穿孔管消声器声学仿真[J]. 噪声与振动控制, 2012, 32(2): 151-154.

HE Yan-song, LI Jing, LU Hui-chao.Acoustic simulation of mufflers with multiple perforated tubes[J]. Noise and Vibration Control, 2012, 32(2): 151-154.

[14]Munjal M L. Acoustics of ducts and mufflers[M]. John Wiley & Sons, 2014.

[15]刘克,焦风雷,乔五之. 微穿孔板吸声体非线性声学特性初探[J]. 声学技术, 2001, 20(3): 135-136.

LIU Ke, JIAO Feng-lei, QIAO Wu-zhi. Rudimentary researches of nonlinear properties of microperforated-panel [J]. Acoustic Technology, 2001, 20(3): 135-136.

[16]何为,薛卫东,唐斌. 优化试验设计方法及数据分析[M]. 北京: 化学工业出版社, 2011: 191-200.

[17]谢宇. 回归分析[M].北京: 社会科学文献出版社, 2013.