金属切削过程刀具磨损信号的混沌特征
2015-12-30关山,彭昶
第一作者关山男,博士,教授,1970年6月生
金属切削过程刀具磨损信号的混沌特征
关山,彭昶(东北电力大学机械工程学院, 吉林132012)
摘要:针对刀具磨损过程中声发射信号非线性特征,提出基于混沌理论的信号分析及特征提取方法。采用延迟时间法对去噪后的时间序列进行相空间重构,分析延迟时间及嵌入维数随刀具磨损的变化规律;用关联维数、最大Lyapunov指数及Kolmogorov熵三种混沌特征参数定量分析刀具在不同切削条件下随磨损量增大所呈现的变化规律。研究结果表明,刀具磨损声发射信号具有明显的混沌特征,三种混沌特征参数、延迟时间及嵌入维数与刀具磨损状态具有明显的对应关系,可用作刀具磨损状态监测、磨损量预测的特征参数。
关键词:刀具状态监测;相空间重构;混沌特征参数
基金项目:吉林省科技厅科技公关计划(20140204004SF)
收稿日期:2014-03-19修改稿收到日期:2014-05-14
中图分类号:TH165.3;TP206文献标志码:A
Chaotic characteristics of tool wear signal during metal cutting process
GUANShan,PENGChang(School of Mechanical Engineering, Northeast Electric Power University, Jilin 132012, China)
Abstract:Aiming at the nonlinear characteristics of acoustic emission signals from tool wear, a method of signal analysis and feature extracting based on the chaos theory was proposed. Here, the phase space reconstruction of denoised time series with the time delay method and the analysis of the variation laws of time delay and embedded dimension versus tool wear were performed firstly. Then, the variation laws of tools with increase in the amount of tool wear under different cutting conditions were analyzed using three chaotic characteristic parameters including correlative dimension, the maximum Lyapunov exponent and Kolmogorov entropy. The results showed that the acoustic emission signals from tool wear have obvious chaos characters, moreover the above three chaotic characteristic parameters, time delay and embedded dimension have significant corresponding relationships with the states of tool wear so that they can be used as parameters for condition monitoring of tool wear states and prediction of the amount of tool wear.
Key words:tool condition monitoring; phase space reconstruction; chaotic characteristic parameters
刀具状态监测技术作为保障工件表面质量与尺寸精度、防止工件报废机床损坏、优化加工过程、降低成本、提高生产效率的有效手段,颇受重视。刀具磨损与切削条件、工件材料、刀具种类等多种因素有关,为典型的非线性、非平稳过程。因此,采用非线性分析方法最直接、最有效。混沌理论因具有能揭示复杂系统表现的非平稳、非线性、不连续等独到之处,被广泛用于非线性系统故障诊断及预测[1-6],但用于刀具磨损状态监测较少[7-8]。
本文通过采集刀具不同磨损阶段的声发射信号,运用混沌分析理论研究刀具在不同磨损阶段采集的监测信号混沌动力学特征,以期找到更有效的信号特征提取方法,提高刀具磨损状态监测及磨损量预测准确率。
1实验系统及试验方法
实验系统见图1,所用PXR30谐振式声发射传感器的谐振频率为300 kHz、带宽80~400 kHz,前置放大器为PXPAⅡ宽带声发射放大器,带宽 15 kHz~2 MHz,增益40 dB。预处理实现对声发射信号带通滤波。用PCI-1721数据采集卡,利用 LabVIEW软件编写数据采集程序完成数据采集,采样频率为1MHz。实验材料为高温合金GH625,刀片为肯纳公司的KC9125硬质合金涂层刀片,采用CKA6136i数控车床进行车削实验。

图1 声发射数据采集系统示意图 Fig.1 Diagram of acoustic emission data acquisitionsystem
实验目的是为研究变切削条件下刀具磨损状态分类及刀具磨损量预测问题,如将切削速度、进给量、切削深度三个可选参数进行全面组合,则会形成多种切削条件,导致实验量过大及由于切削速度对刀具寿命影响远大于其它两因素,过大切削速度变化范围会导致变切削条件下分类与预测准确率下降。因此将切削速度参数依据相近原则分成3组,见表1,针对每组与其它两因素的三种水平进行3因素3水平正交试验。

表1 各组正交实验所选用的切削速度
据表1,选定切削条件的实验方法为:① 取刀片1切削10 s后停车,仅采集切削过程中6~10 s之间数据,取下刀片,利用工具显微镜测量后刀面磨损量VB值大小。② 更换刀片2,切削20 s后停车,只记录15~20 s之间数据,取下刀片测量VB值。③ 更换新刀片,切削时间较上次增加10 s记录切削时间内最后5 s数据停车,取下刀片,测量VB值。④ 步骤③反复进行,每次切削均更换新刀片,切削时间均较上次增加10 s,直到切削时间累加到足够长、新刀片在此切削时间内能磨损为止,切削实验终止。⑤ 选另一切削条件,重复①、②、③、④实验,直至完成全部选定切削条件实验。
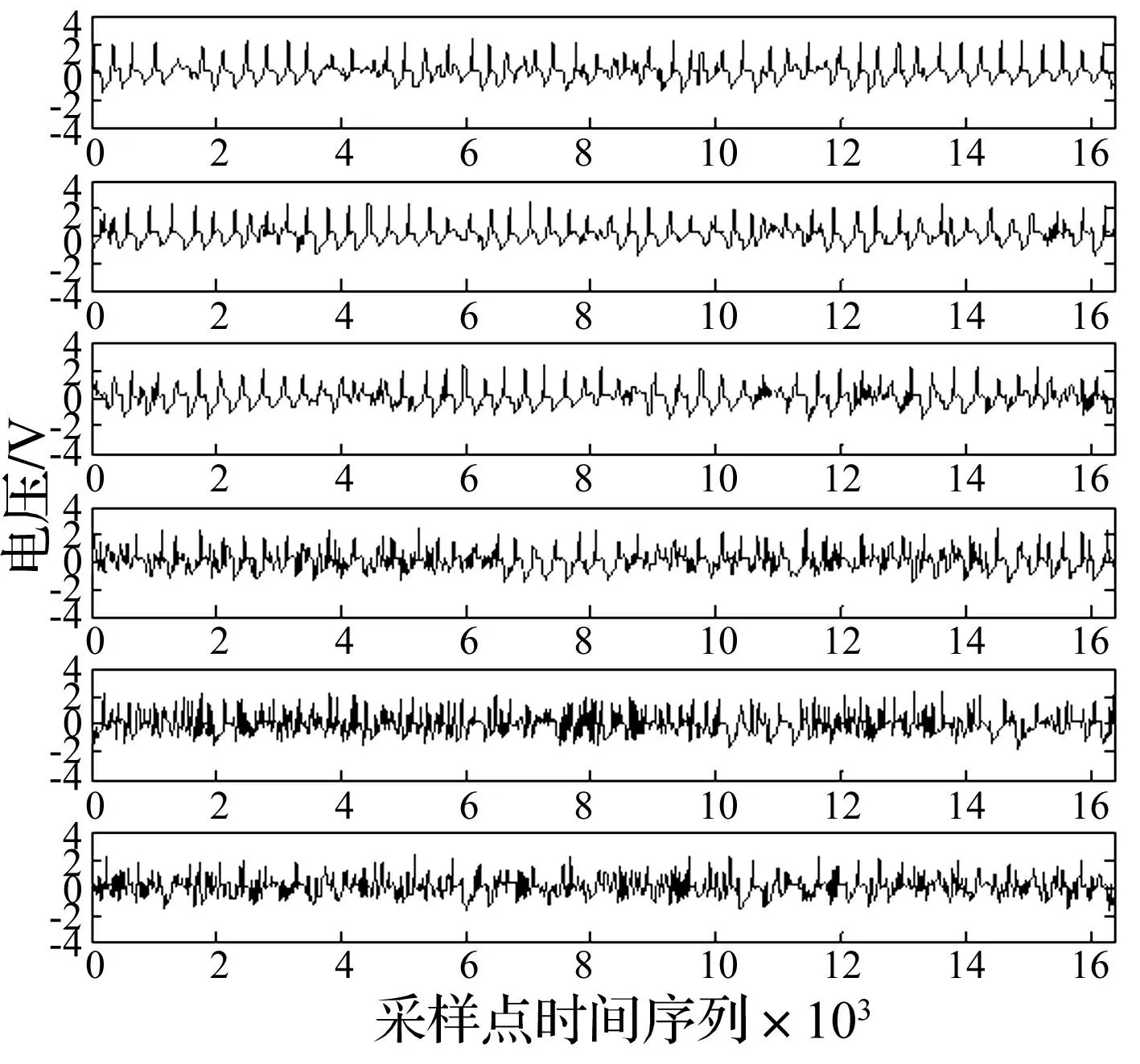
图2 刀具不同磨损阶段采样信号时序图 Fig.2 Timing diagram of different wear stages sampled signal
该实验方法与实际切削过程相符,每次切削仅记录最后5 s的数据,不仅能减少数据采集量,且该段数据对应刀具当前磨损状态。采用切削时间逐步递增方式便于标定切削时间、刀具磨损量及信号特征间对应关系,为建立刀具磨损量曲线回归方程,实现磨损量预测准备数据条件。
本文以切削速度560 r/min、进给量0.3 mm/r、切削深度0.4 mm时采集的数据为例进行说明,所有数据均采用相空间重构结合奇异值分解法去噪。图2为不同磨损阶段采样信号的时序图,自上而下分别对应VB值为0.11、0.13、0.17、0.24、0.26、0.31。
2时间序列信号混沌分析基础
混沌分析为通过混沌吸引子及混沌特征量,如关联维D2、 Kolmogorov熵及Lyapunov指数表征被研究系统的非线性动力学行为。时间序列信号是动力系统中全部物理因子相互作用的综合反映,蕴藏参与系统动态变化的全部变量的迹,因此用系统一个观察量即可重构整个原系统模型,即为相空间重构[9-11]。
2.1相空间重构理论
为重构一个与原始系统拓扑等价的状态空间,只需考察一个分量时间序列,并将其在某些固定时间延迟点的测量作为新维处理,其可确定某个多维状态空间中一点。重复此过程并测量不同时间的各延迟量即可产生诸多此类点,亦即代表系统的时间演化。
相空间重构关键在于选取τ,m,若选取不合理会直接导致重构的相空间不能充分恢复系统的动力学行为。设时间序列x(t),t=1,2,…,n,适当选嵌入维数m及延迟时间τ=kΔt(Δt为两次相邻采样时间间隔,k为整数),重构相空间为
(1)
式中:M=n-(m-1)τ为重构相空间样本数。
2.2延迟时间τ的选取
若τ选的太小,致重构相空间矢量中任意两分量在数值上非常接近,无法提供两独立坐标分量;但τ太大,则两坐标在统计意义上又是完全独立的,致混沌吸引子轨迹在两方向的投影无相关性。恰当选取τ可在最小嵌入空间内对相邻轨道实行最优分离,见图3。自相关函数法为成熟的求时间延迟方法。混沌时间序列x(t),(t=1,2,…,n)的时间跨度jτ的自相关函数为
(2)
式中:n为序列总点数,做出自相关函数关于时间t的图像。
当自相关函数下降到初始值的1-1/e倍时,所得时间即为重构相空间的时间延迟,见图4。
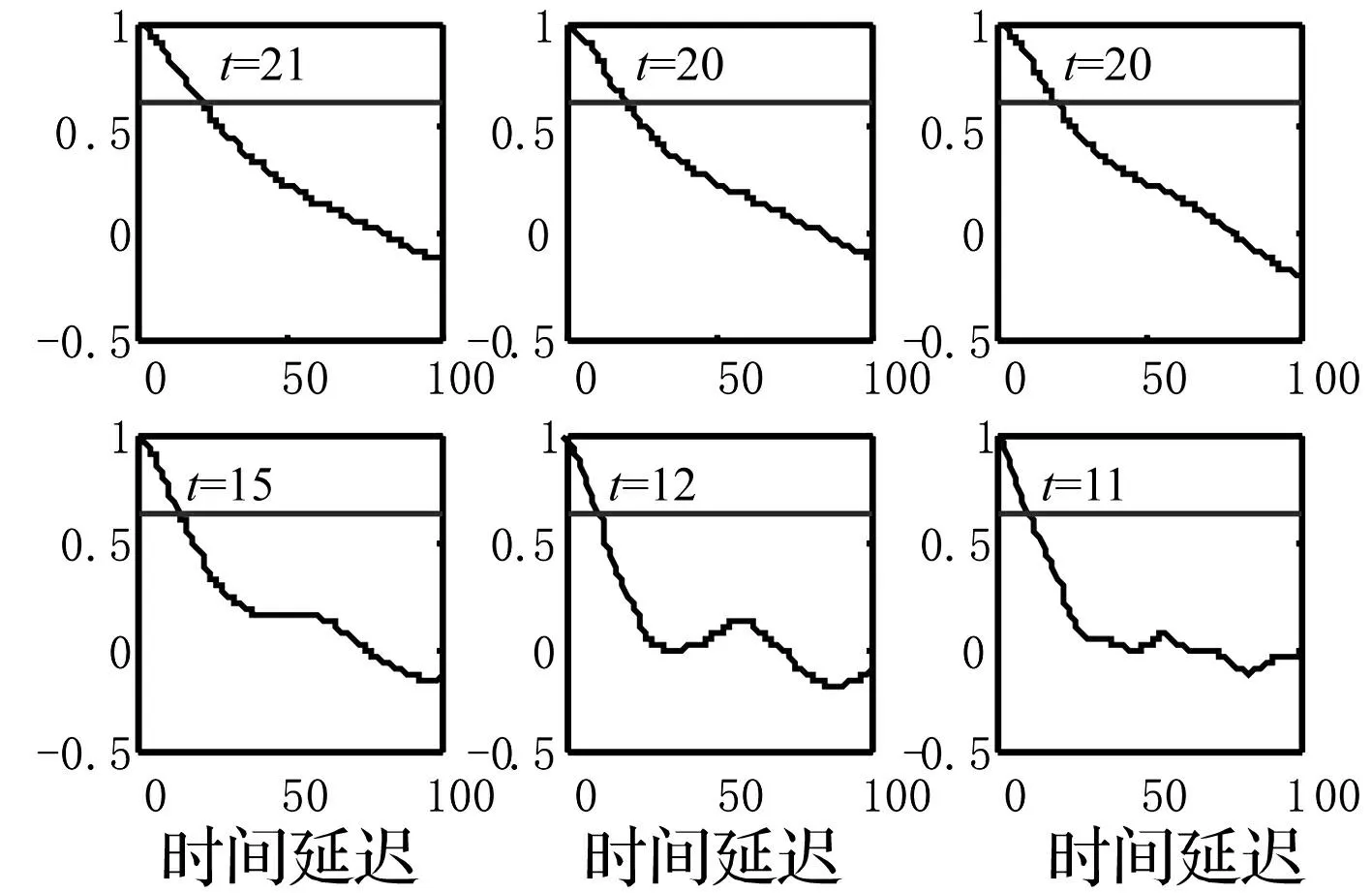
图3 不同磨损阶段延迟时间的选取 Fig.3 Delay time selection of different wear stages

图4 不同切削条件下磨损量与延迟时间关系曲线 Fig.4 Curve of amount of wear and delay time under different cutting conditions
由图3、图4看出,τ值随刀具磨损量增加总体趋势减小。由于损量增加致刀具与被加工件摩擦加剧、声发射现象增加,导致单位时间内振铃计数增加,从而使最大相关时间减小。因此τ可间接反映声发射现象参数-振铃计数大小。
2.3最佳嵌入维数m的选取
为保证原始吸引子与重构吸引子拓扑等价,嵌入维数m选取应适当。m太小重构吸引子会发生折叠甚至某处出现自相交,重构吸引子形状与原始吸引子完全不同;m太大,吸引子几何结构完全被打开,不仅会增加计算量,亦会放大噪音污染作用。因此,恰当选择m,既能保证准确计算各混沌不变量,又能降低计算量及噪声影响。本文用虚假最近邻点法计算嵌入维数。
(3)
维数增加到m+1时,其距离变为
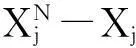
(4)
若Rm+1(j)较Rm(j)大很多,则可认为因高维吸引子中2个不相邻点投影到低维轨线时变成相邻两点造成,该邻点即为虚假邻近点。若
(5)

(6)

对实测时间序列嵌入维数从2开始,计算虚假最邻点比例,逐渐增加m直到虚假最近邻点比例小于5%或不随m增加而减小时,可认为吸引子完全打开,此时的m即为嵌入维数。图5为刀具不同磨损阶段假近邻率随嵌入维数变化的关系曲线。
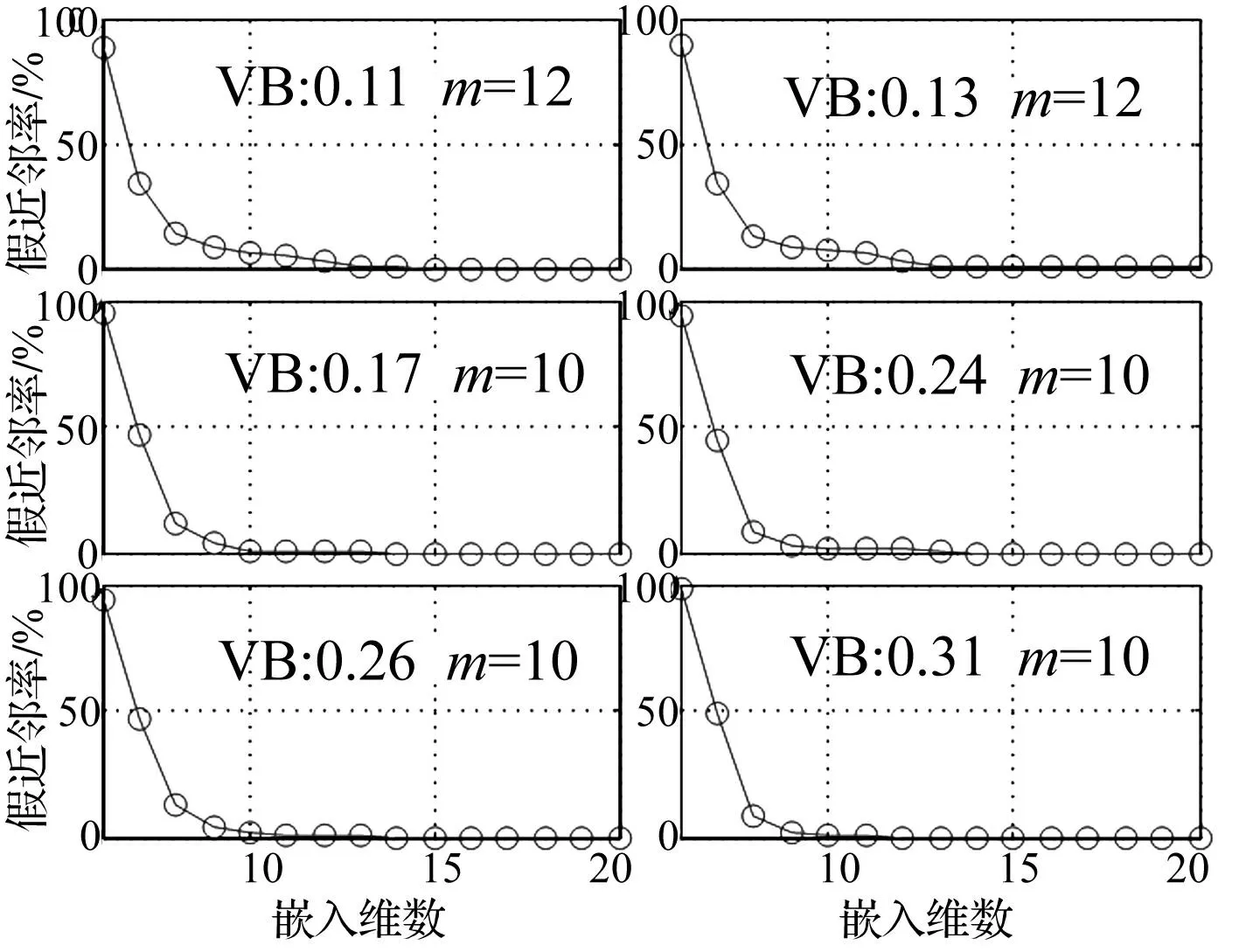
图5 不同磨损状态下嵌入维数 Fig.5 Embedding dimension under different wear conditions
通过计算不同切削条件下采样信号的嵌入维数发现,随刀具磨损量增大嵌入维数呈减小趋势。表2为不同磨损量下嵌入维数取9~13时,假邻近率的取值。由表2看出,对应每个嵌入维数,刀具磨损量增加假邻近率总体呈减小趋势。其中有底纹部分为假邻近率小于5%时所选最佳嵌入维数。
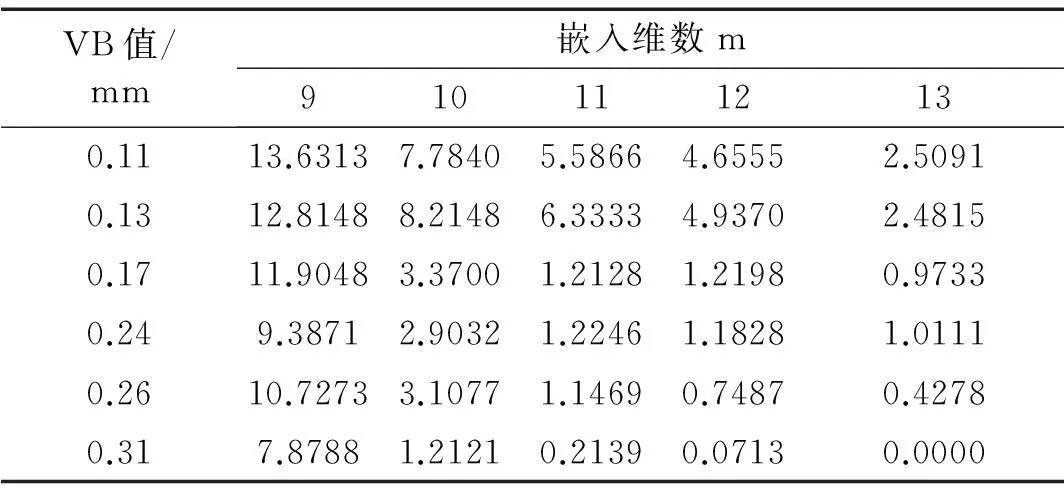
表2 假邻近率与嵌入维数变化关系表
将采样信号按所选τ及m进行相空间重构,所得吸引子二维图见图6。由图6可见,不同磨损阶段吸引子轨道始终在一定范围内伸缩变化,在局部无序,具有复杂的拉伸、扭曲、折叠及无穷嵌套的自相似架构,符合奇异吸引子特点,具有混沌特性。对比不同磨损阶段信号吸引子图看出,刀具磨损量增加,吸引子向四周膨胀并拉长,在刀具磨损的初期阶段尤其明显。
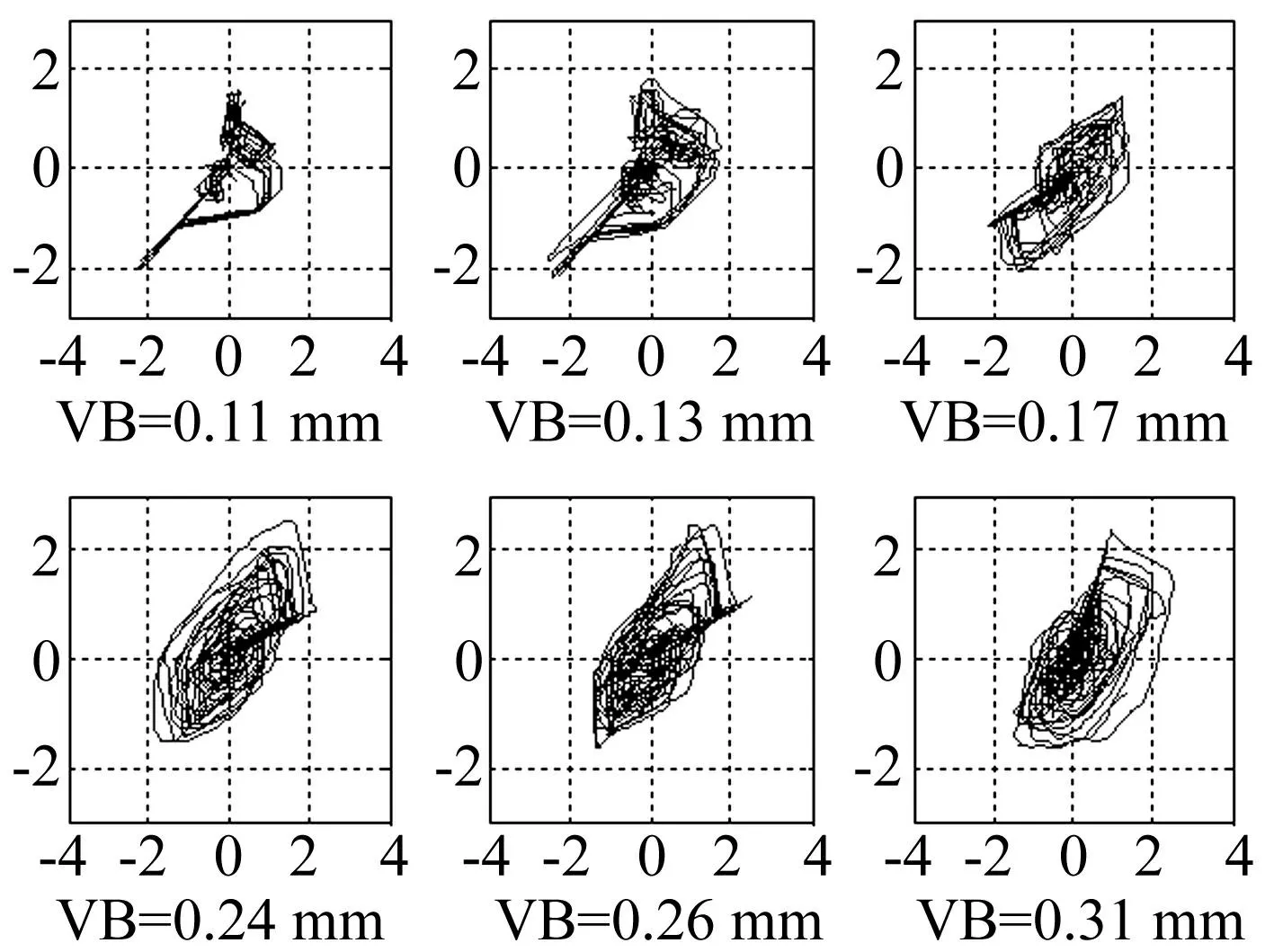
图6 刀具不同磨损状态吸引子图 Fig.6 Attractor figures of different wear conditions
3刀具磨损信号的混沌特征
在机械设备状态监测与故障诊断中,对因机械系统状态变化引起的吸引子结构变化常用关联维数、最大Lyapunov指数、Kolmogorov熵等[12-15]混沌特征量描述。
3.1关联维数对刀具不同磨损阶段表述
随刀具磨损程度增加,吸引子随之发生变化,反映吸引子复杂程度的分维数亦发生变化。在众多分形维数中关联维数对吸引子的不均匀性反应最敏感,能反映吸引子的动态结构,且求关联维数的G-P算法简单可靠,故本文采用G-P算法求关联维数,研究关联维与刀具不同磨损状态间关系。刀具磨损量0.11 mm时嵌入维数与关联维数关系曲线见图7。图7(a)中红色区域为线性无标度区,最上一条曲线对应m=2,最下一条曲线对应m=20。可见m增加无标度区直线逐渐平行,即直线斜率趋于饱和,此互相平行的直线段斜率即为最佳关联维数D2。图7(b)为随嵌入维数m增加线性无标度区直线斜率变化情况,当嵌入维数m>10后线性无标度区直线斜率不再随m增加而增加,趋于饱和,此即计算的最佳关联维数为1.502 9,信号表现为混沌[16]。
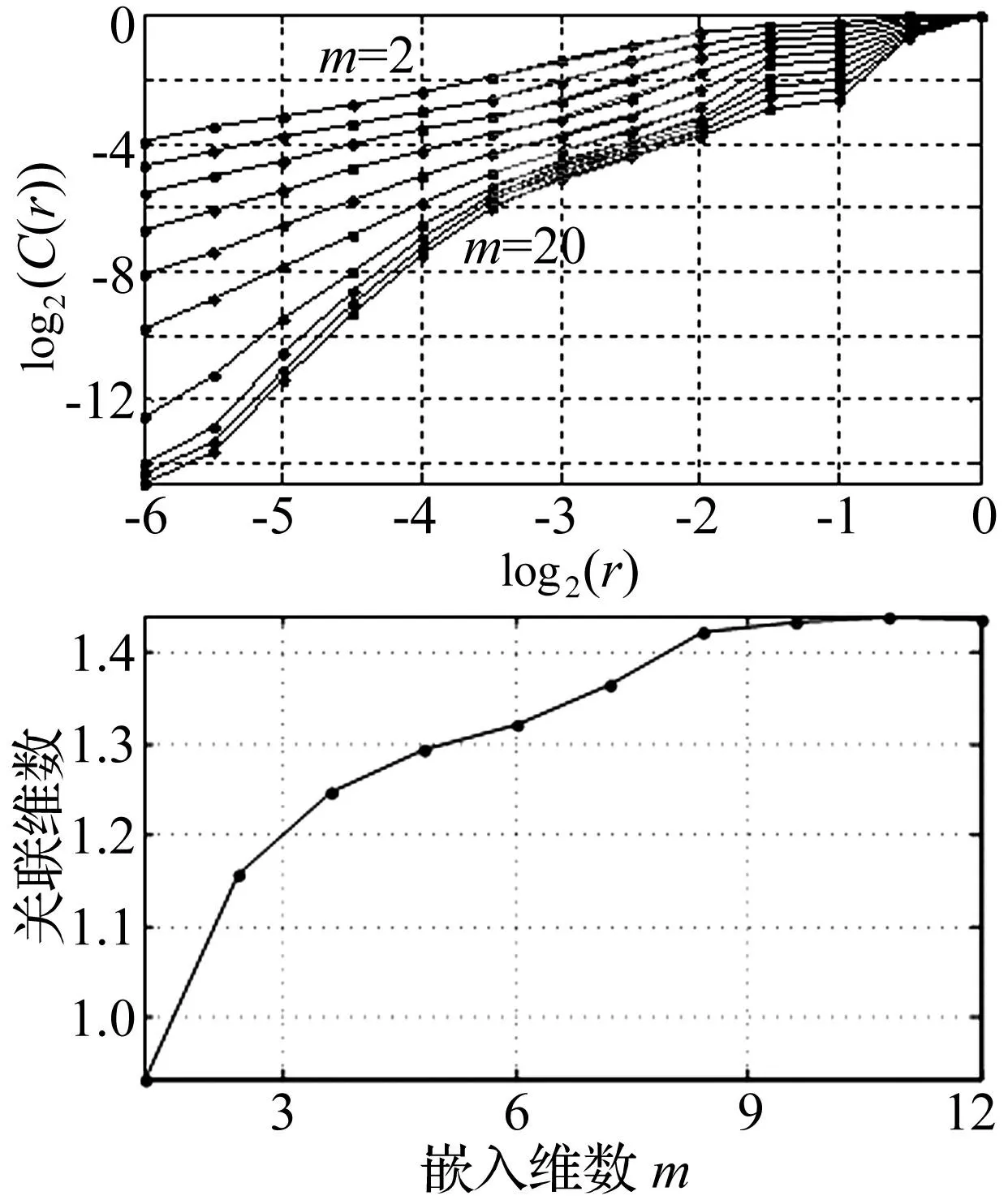
图7 嵌入维数与关联维数关系曲线 Fig.7 Curve ofembedding dimension and correlation dimension
对不同切削条件下所得刀具各磨损状态下数据计算发现,随刀具磨损量增加关联维呈上升趋势,见图8。据已有实验数据计算结果,关联维大小与刀具磨损量关系见表3。
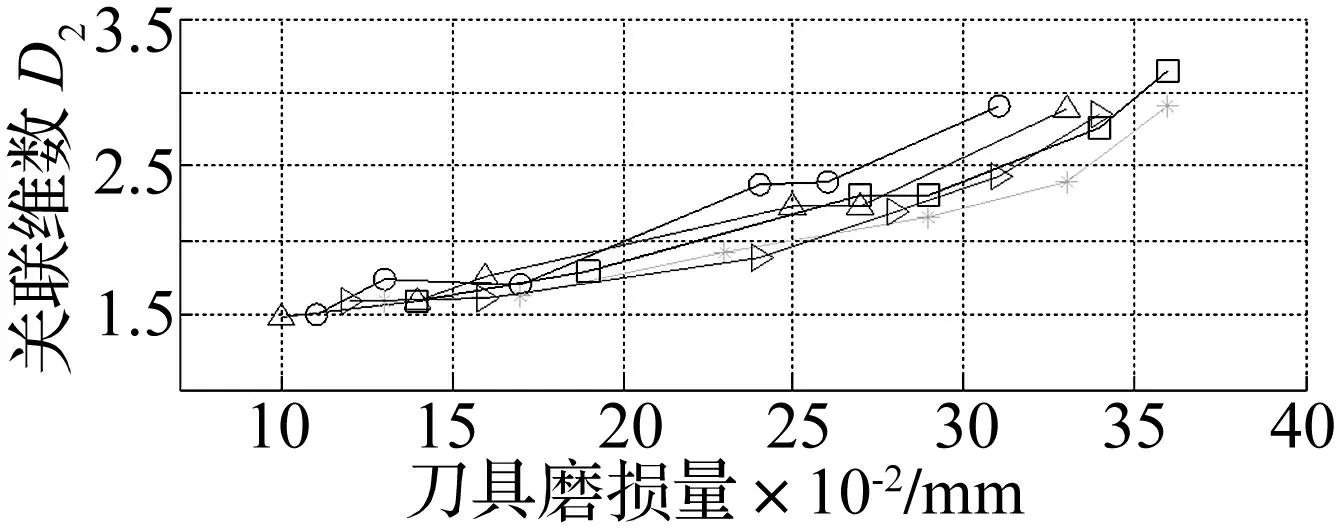
图8 磨损量与关联维关系曲线 Fig.8 Curve ofamount of wear and correlation dimension

VB值VB<0.20.2
3.2Lyapunov指数
Lyapunov指数是刻画奇异吸引子性质的一种测度与统计量,表征系统在相空间中两个初值较近轨道间收敛或发散的平均指数率。n维向空间中存在n个Lyapunov指数,正Lyapunov指数表明在该维方向系统运动轨道迅速分离,长期行为对初始条件敏感,表现出混沌特性。对奇异吸引子而言,最大Lyapunov指数为正,且数值越大说明系统的混沌程度越强。本文采用小数据量法计算最大Lyapunov指数[17]。计算流程见图9。
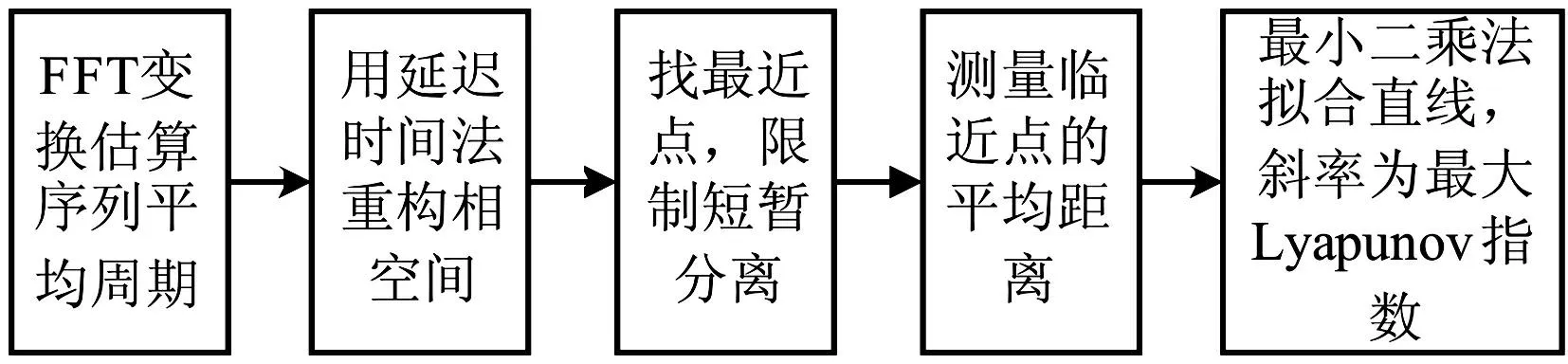
图9 小数据法计算最大Lyapunov指数流程图 Fig.9 Flow chart of calculating the maximum Lyapunov exponent with small data method
图10为刀具磨损量达到0.17 mm时,基本轨道第j对最邻近点经i个离散时间步长后距离dj(i)的演化曲线。图10(a)中红色部分为用最小二乘法拟合后所得有最大斜率的直线段,求得该线性区斜率, 即为最大Lyapunov指数,见图10(b)。计算得最大Lyapunov指数λ1=0.231 8。
用该方法对不同切削条件、磨损阶段的采样数据计算最大Lyapunov指数,结果见表4。由表4看出,随刀具磨损量增加最大Lyapunov指数呈现变大趋势,说明信号的混沌特征增强。

表4 刀具磨损量与Lyapunov指数关系
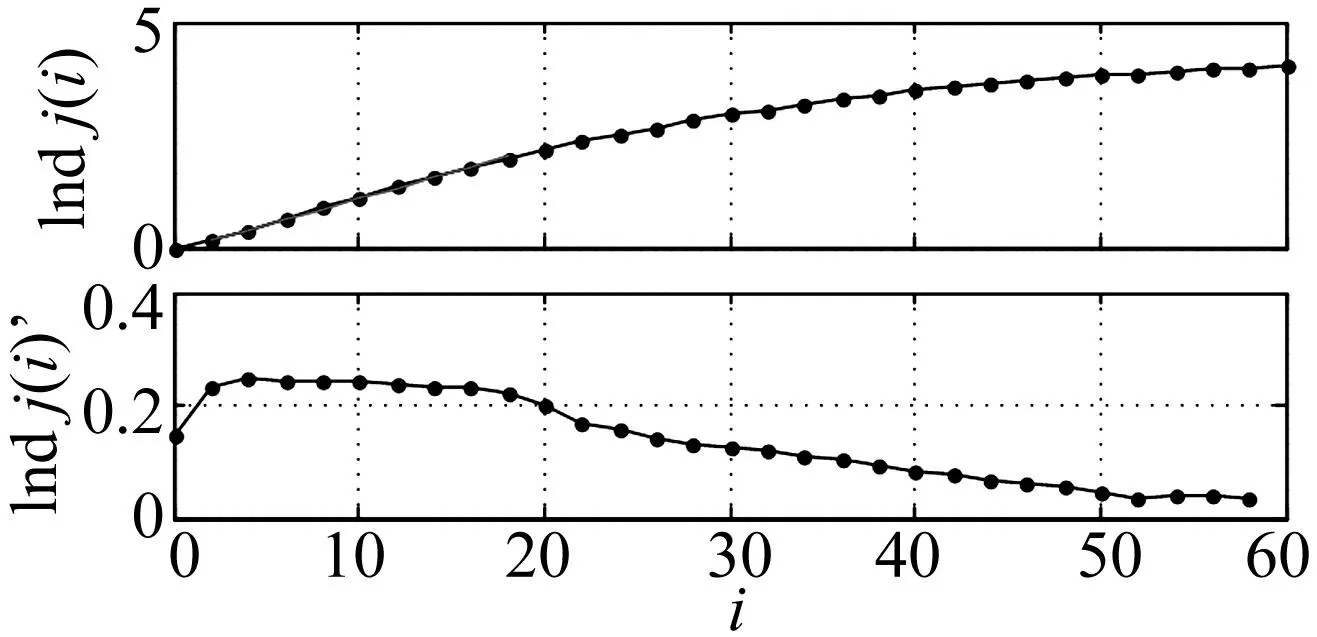
图10 线性区域及最大Lyapunov指数选择曲线 Fig.10 Range of linearity and the maximum Lyapunov exponent selection curve
3.3Kolmogorov熵
K熵不仅可用于混沌特征定性识别,也可用于描述动态系统混沌程度,代表相空间轨道信息随时间损失率的平均值,表征系统可预测度。对系统演化过程中无信息产生及丢失的规则运动K熵为0;对信息完全丢失的随机运动K熵趋于无穷;若K熵取有限正值,表示系统做混沌运动,且K熵越大系统信息损失速率越大,系统混沌程度越高,系统越复杂。因此通过K熵计算可对系统状态进行评价。图11为刀具在不同磨损阶段,K熵随嵌入维数变化关系曲线。对每个磨损状态,改变嵌入维数计算K熵,取最小值时即为此磨损阶段的K熵。由图11、表5看出,随磨损量增加K熵逐渐变大,与Lyapunov指数变化趋势一致。且K熵均为有限正值,说明在金属切削过程中刀具磨损发出的信号处于混沌状态。
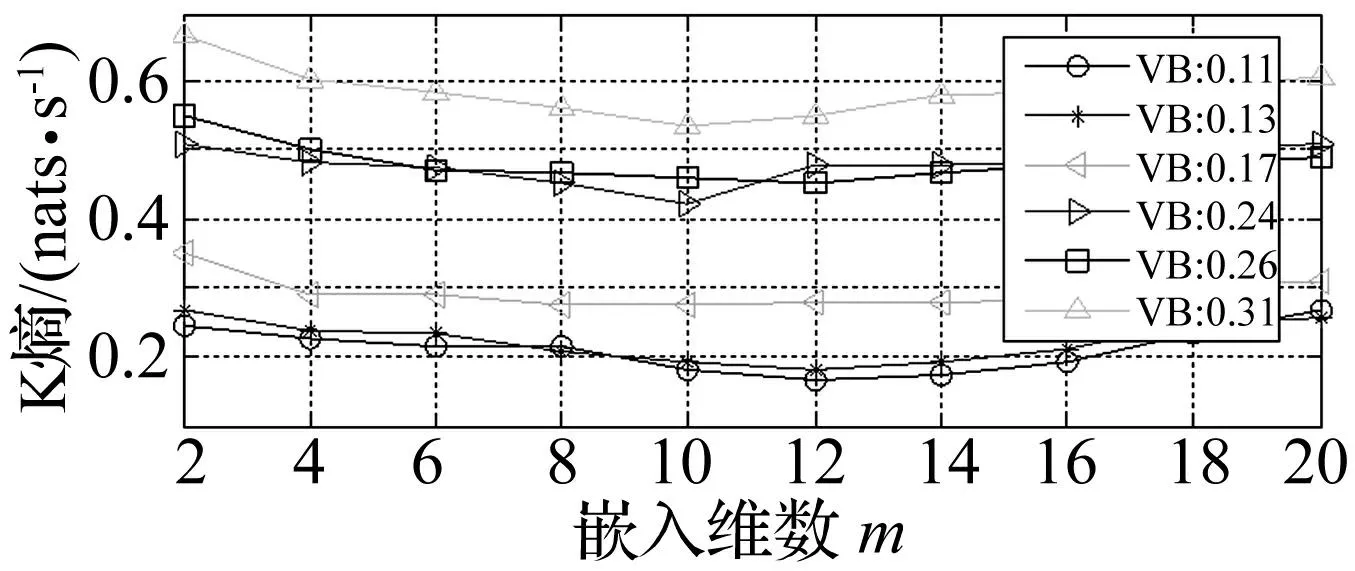
图11 K熵随嵌入维变化关系曲线 Fig.11 Curve of Kentropy change with embedding dimension
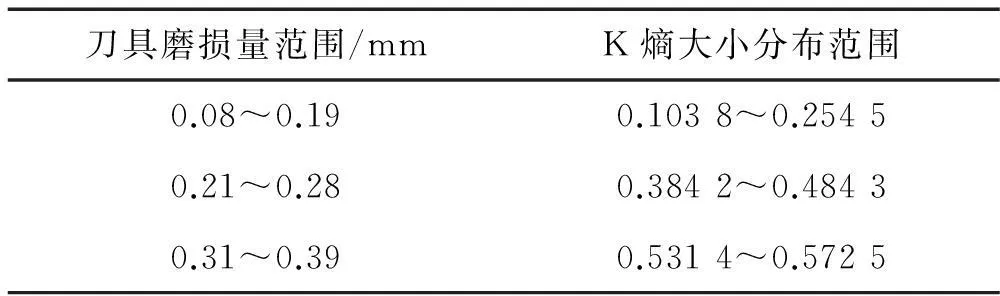
刀具磨损量范围/mmK熵大小分布范围0.08~0.190.1038~0.25450.21~0.280.3842~0.48430.31~0.390.5314~0.5725
Lyapunov指数及K熵不仅表征系统的混沌特性,且可用于解决可预测性期限的定量度量问题。1/K代表系统误差每增长一倍经历的时间,其可估计在一定精度要求下可能预测时间长度,作为动力系统的平均可预测尺度,而系统最大可预报时间尺度则由最大Lyapunov指数倒数定义。随刀具磨损,Lyapunov指数及K熵均不断增大,刀具磨损量可预测时间尺度越小,尤其在刀具进入剧烈磨损阶段后,磨损量几乎不可预测。
4结论
(1)金属切削过程中刀具磨损产生的声发射信号具有较强混沌特征。用混沌理论分析采样信号能更好提取信号特征。
(2)通过对关联维数D2、Lyapunov指数及Kolmogorov熵定量计算知,切削条件、刀具磨损状态不同时,混沌特征量与刀具磨损有极强的对应关系。结合延迟时间、嵌入维数及其它算法提取的信号特征向量,可较好定位刀具的磨损状态,实现刀具磨损量预测。
参考文献
[1]关贞珍,郑海起,杨支涛,等. 基于非线性几何不变量的轴承故障诊断方法研究[J]. 振动与冲击,2009, 28(11):130-133.
GUAN Zhen-zhen, ZHENG Hai-qi, YANG Zhi-tao, et al. Fault diagnosis of bearing based on nonlinear time series of geometrical invariants[J].Journal of Vibration and Shock, 2009, 28(11): 130-133.
[2]张雨. 柴油机活塞环胶结信息的符号李指数含噪辨识[J]. 内燃机学报, 2010,28(1): 90-95.
ZHANG Yu. Identification of information of diesel piston ring sticking with noise based on symboilic-lyapunov index[J]. Transactions of CSICE, 2010,28(1):90-95.
[3]马晋, 江志农,高金吉. 基于混沌分形理论的特征提取技术在气阀故障诊断中应用[J]. 振动与冲击,2012, 31(19):26-30.
MA Jin, JIANG Zhi-nong, GAO Jin-ji. Feature extraction method based on chaotic fractal theory and its application in fault diagnosis of gas valves[J]. Journal of Vibration and Shock, 2012, 31(19): 26-30.
[4]Xue Jie-ni, Shi Zhong-ke. Short-time traffic flow prediction based on chaos time series theory[J]. Journal of Transportation Systems Engineering and Information Technology, 2008,8(5): 68-72.
[5]史丽晨, 段志善. 基于混沌-分形理论的往复式活塞隔膜泵磨损故障分析[J]. 农业机械学报,2010, 41(4): 222-226.
SHI Li-chen, DUAN Zhi-shan. Wearing fault diagnosis of reciprocating membrane pump based on chaos and fractal theory[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010,41(4):222-226.
[6]Guo Jun, Zhou Jian-zhong, Qin Hui,et al. Monthly streamflow forecasting based on improved support vector machine model[J]. Expert Systems with Application, 2011, 38(10): 13073-13081.
[7]张蕾. 非线性时间序列的高阶统计特征提取和趋势分析[D]. 沈阳:沈阳航空航天大学, 2013.
[8]张锴锋,袁惠群,聂鹏. 基于广义分形维数的刀具磨损状态监测[J]. 振动与冲击, 2014,33(1):162-164.
ZHANG Kai-feng,YUAN Hui-qun,NIE Peng.Tool wear condition monitoring based on generalized fractal dimensions[J].Journal of Vibration and Shock, 2014, 33(1):162-164.
[9]Shi Jing-zhuo, Zhao Fu-jie, Shen Xiao-xi,et al. Chaotic operation and chaos control of traveling wave ultrasonic montor[J]. Ultrasonics, 2013,53(6):1112-1123.
[10]Ma Hui-zhu, Li Cheng-xiang. Research on parameters estimation of sea clutter in data preprocessing[J]. Optik-International Journal for Light and Electron Optics, 2013,124(5):901-905.
[11]Nie Zhen-hua, Hao Hong, Ma Hong-wei. Structural damage detection based on the reconstructed phase space for reinforced concrete slab: Experimental study[J]. Journal of Sound and Vibration, 2013, 332(4):1061-1078.
[12]Patel V N, Tandon N, Pandey P K. Defect detection in deep groove ball bearing in presence of external vibration using envelope analysis and duffing oscillator[J]. Measurement, 2012, 45(5):960-970.
[13]于大鹏,赵德有. 螺旋桨鸣音的混沌动力特性研究[J]. 振动与冲击,2009,28(12): 47-52.
YU Da-peng, ZHAO De-you. Chaotic dynamics of propeller singing[J]. Journal of Vibration and Shock, 2009, 28(12): 47-52.
[14]Shayegh F, Sadri S, Amirfattahi R, et al. A model-based method for computation of correlation dimension, Lyapunov exponents and symchronization from depth-EEG signals[J]. Computer methods and programs in biomedicine, 2014,113(1):323-337.
[15]修妍. 混沌时序分析中的若干问题及其应用研究[D]. 天津:天津大学, 2007.
[16]张英堂,任国全,李国璋. 柴油机振动信号分形特征诊断的改进算法[J].内燃机学报,2006,24(5):459-464.
ZHANG Ying-tang, REN Guo-quan, LI Guo-zhang. Improved algorithm of diesel engine diagnosis based on fractal dimension of vibration signals[J]. Transactions of CSICE,2006,24(5):459-464.
[17]杨永锋,仵敏娟,高喆,等.小数据量法计算最大Lyapunov指数的参数选择[J].振动、测试与诊断,2012, 32(3):371-374.
YANG Yong-feng, WU Min-juan, GAO Zhe, et al. Parameters selection for calculating largest lyapunov exponent from small data sets[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(3):371-374.