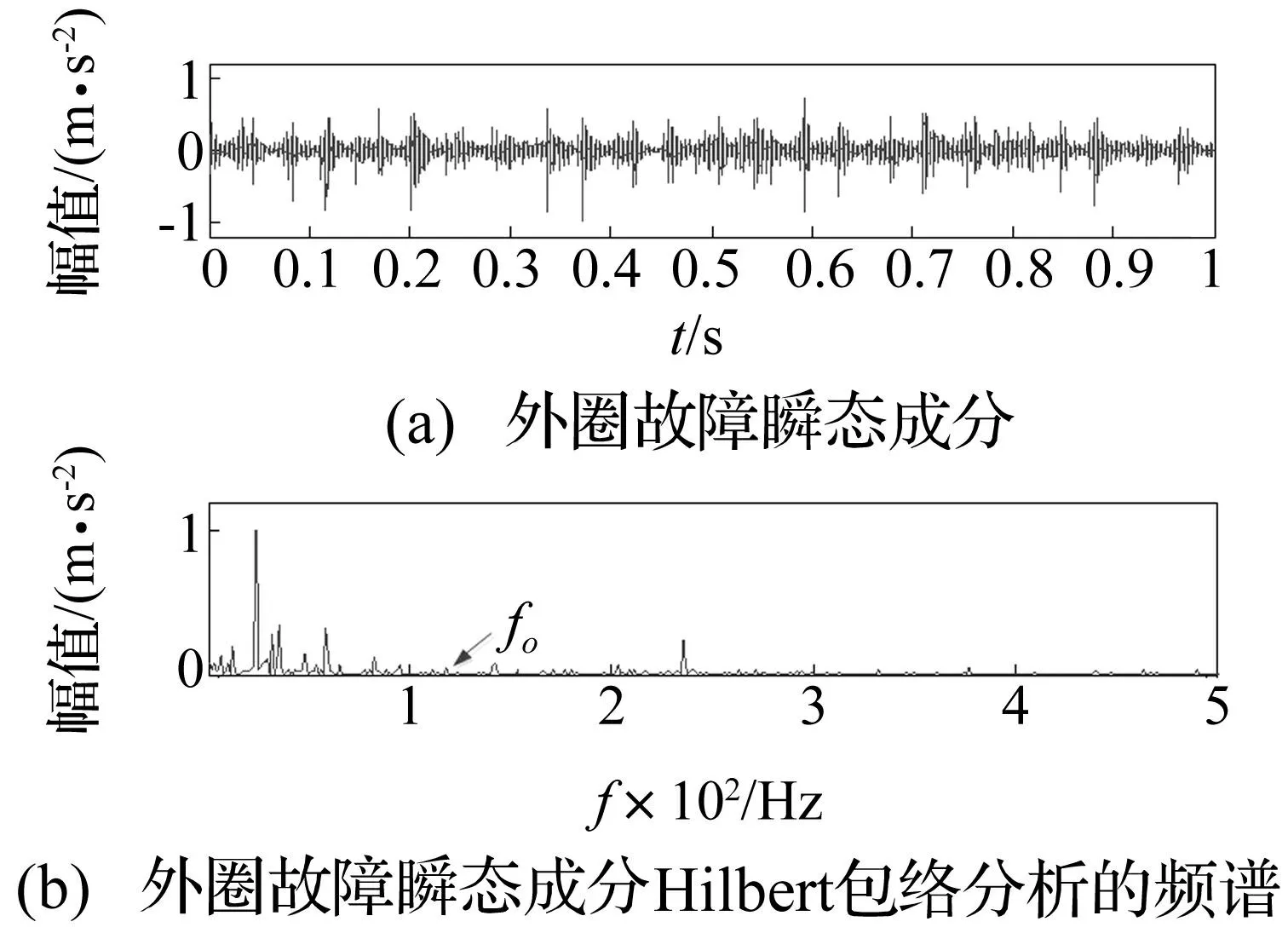
基于双调Q小波变换的瞬态成分提取及轴承故障诊断应用研究

第一作者项巍巍男，硕士生，1990年生

通信作者蔡改改女，博士，讲师，1986年生

基于双调Q小波变换的瞬态成分提取及轴承故障诊断应用研究

项巍巍，蔡改改，樊薇，黄伟国，朱忠奎(苏州大学城市轨道交通学院，江苏苏州215137)

摘要：因轴承的剥落、裂纹等局部故障易致运行时振动信号中出现瞬态成分，而轴承故障振动信号为非平稳信号，含高、低振荡成分，传统的线性信号处理方法及基于频率的分解方法均存在一定局限性。对此，研究基于信号振荡特征而非频率特征的双调Q小波变换，设定不同Q因子小波将轴承故障信号非线性分解成低、高振荡及噪声成分，轴承故障瞬态成分对应低振荡成分，提取低振荡成分即能实现轴承故障瞬态成分提取。通过轴承故障状态下瞬态成分检测表明，该方法能有效提取轴承故障瞬态成分。经与均值滤波、小波阈值及经验模态分解(EMD)等方法比较，验证该方法的优越性。

关键词：滚动轴承；故障诊断；双调Q小波变换；振荡特征

基金项目：国家自然科学基金资助项目(51375322)

收稿日期：2014-01-08修改稿收到日期：2014-05-20

中图分类号:TH165.3文献标志码：A

Transient feature extraction based on double-TQWT and its application in bearing fault diagnosis

XIANGWei-wei,CAIGai-gai,FANWei,HUANGWei-guo,ZHUZhong-kui(School of Urban Rail Transportation, Soochow University, Suzhou 215137, China)

Abstract:Local faults in rotating machinery bearings are easy to cause transient impulse response components in vibration signals. In order to realize bearing fault diagnosis under strong noise conditions, it is crucial to extract fault features from vibration signals. But a bearing fault vibration signal is a non-stationary one, it consists of high and low resonance components, traditional linear methods and signal decomposition methods based on frequency have certain limitations. To overcome these limitations, a nonlinear signal analysis method named double tunable Q-factor wavelet transformation (double-TQWT) was proposed, it was based on signal resonance characteristics rather than frequency features. By using the double-TQWT, a bearing fault vibration signal was decomposed into high and low resonance components based on different resonance characteristics. The bearing fault transient component had a low Q-factor and was decomposed into low resonance components. Extracting these low resonance components could realize extracting bearing fault transient components. The transient components for bearing fault signals under strong noise conditions were extracted and analyzed. The results showed that the new method is superior to the average filtering method，the wavelet threshold algorithm, and the EMD.

Key words:rolling bearing; fault diagnosis; double-TQWT; resonance characteristic

轴承元件出现剥落、裂纹等局部故障时，在运行过程中会引起故障部位较大的瞬时应力，严重影响设备运行质量及生产安全。及时识别设备中故障的萌生及演变对保障机械系统安全运行、减少或避免重大灾难性事故具有重要意义[1]。轴承局部故障振动特征表现为强噪声背景下瞬态响应，为获得可靠故障分析结果，须对振动信号进行处理获得故障瞬态成分，因此轴承故障诊断关键为如何从振动信号中提取该成分[2]。

故障轴承运行中产生的冲击振动呈振荡衰减响应波形，具有持时短、频带宽等特点，且随故障程度发展特征波形会发生相应变化[3]。目前轴承故障诊断较常用的主要有时频分析及高频解调分析等，但均存在不足。由于①轴承故障振动信号为非线性非平稳信号；②轴承故障信号往往表现为高频信号被低频信号调幅特征，而噪声等干扰成分存在于整个频带范围，常用的基于频率方法并不能有效去除与故障瞬态成分同频带的干扰信号；③有些轴承故障产生的故障瞬态成分较微弱，而机器运转时背景噪声较大，故障瞬态成分常淹没其中难识别。

小波变换本质为内积变换，通过将信号与选定小波基函数进行内积变换分析信号[4]，尤其对分段连续、奇异性信号，因此小波变换颇受机械设备状态监测与故障诊断领域关注，基于小波变换的故障诊断取得较大发展[5-7]。然而，传统基于时频特征的小波变换存在基函数选取困难、时频域不能同时满足高分辨率要求等问题，有时低频率分辨率会导致故障瞬态成分被划到相邻频带。因轴承故障振动信号频域范围广，噪声等干扰信号成分分布于整个频域，对与故障瞬态成分同频带的干扰成分，传统仅基于频率特征的小波变换不能有效区分。

由Selesnick等[8-10]提出的基于信号振荡特征而非频率特征的小波变换—调Q小波变换为完全离散的小波变换，可据信号特征，自适应调节小波基函数的Q值，使小波基函数振荡程度与分析信号所需提取成分的振荡程度能较好匹配，从而达到提取目标成分目的。然而实际轴承故障信号含低振荡故障瞬态、高振荡谐波及噪声成分，单个调Q小波并不能较好描述轴承故障振动信号特征。本文基于调Q小波变换，提出基于双调Q小波变换的轴承故障瞬态成分提取方法，即据轴承故障振动信号特征设定高、低Q值小波，获得高、低Q值TQWT的基函数库及相应变换系数，利用形态学成分分析方法据信号中不同成分振荡特征的形态学差异性，非线性分解出故障信号中低振荡瞬态成分。并用于实际轴承故障瞬态成分检测，成功提取出轴承故障瞬态成分，验证该方法的有效性。将基于振荡特征方法与均值滤波、小波阈值[11]及经验模态分解(EMD)[12]相比，进一步验证该方法在强噪声背景下轴承故障瞬态成分提取的优越性。

1双调Q小波变换

1.1调Q小波变换原理

调Q小波变换是一种灵活的离散小波变换。直接在频域上定义Q因子值为脉冲信号中心频率与带宽比值。据信号振荡特征不同，小波变换的品质因子Q灵活可调。其三个重要参数为表征信号振荡程度的Q因子、冗余度γ及分解层数J。调Q小波变换分解滤波器框图见图1，其中LPS表示低通尺度，HPS表示高通尺度。通过迭代用一系列二通道滤波器组实现信号分解，一旦给定Q值、冗余度γ，高、低通尺度β值、α值相应确定，即

(1)

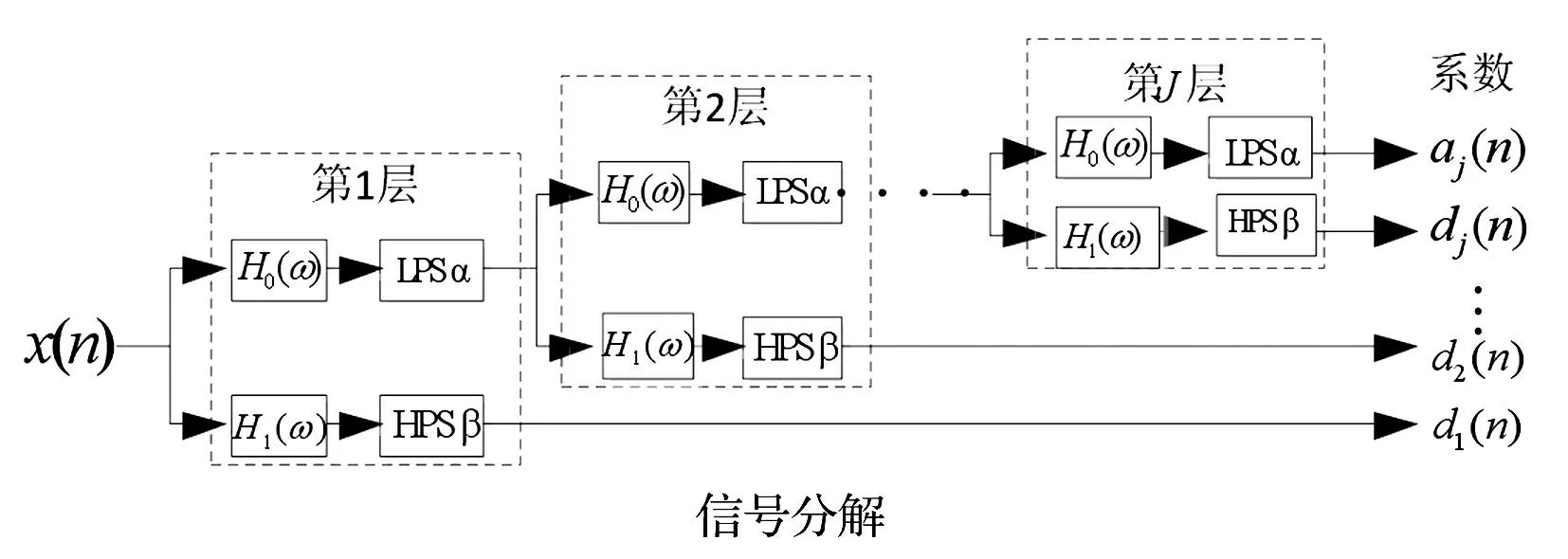
图1　调Q小波变换分解滤波器框图 Fig.1 Block diagram of analysis filter banks

为较好重构信号，滤波器组须严格采样，因此α值、β值须严格满足条件

0<α<1，0<β≤1,α+β>1

(2)

高、低通滤波器的频率响应函数H0(ω)及H1(ω)则需满足

(3)

定义高、低通滤波器频率响应函数H0(ω)及H1(ω)分别为

(4)

(5)

1.2双调Q小波变换原理

TQWT本质为将信号与小波基函数进行内积变换分析信号。区别在于，TQWT能据待分析信号的振荡特征调节小波基函数的Q值，使其更好匹配于待分析信号。分析高振荡信号时用高Q值TQWT，分析低振荡信号时则用低Q值TQWT。然而，实际测得轴承故障信号往往同时含高振荡谐波成分、低振荡瞬态成分及噪声成分，仅用单个TQWT并不能较好表示轴承故障信号特征，需用两个不同Q值TQWT研究此类信号。

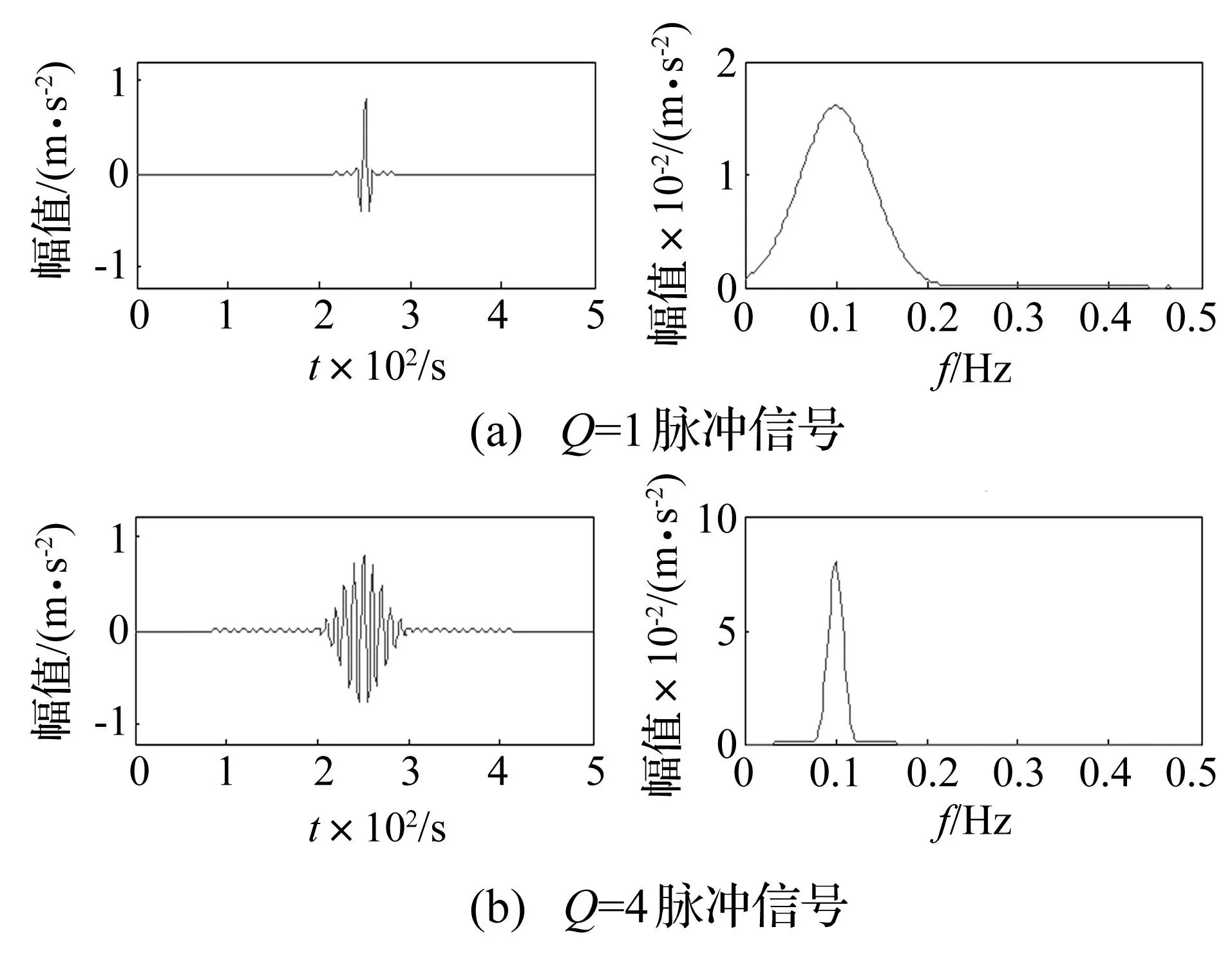
图2　不同Q因子脉冲时、频谱图 Fig.2 The time domain waveform and its spectrum of different signals characterized by its Q-factor

设某信号含两个中心频率相同、振荡程度不同的脉冲成分，此时仅基于频率的分解方法难以将两成分有效区分，见图2。考虑两成分振荡程度及Q值不同，本文从信号振荡特征出发，结合形态学成分分析及分裂增广拉格朗日收缩算法，基于双调Q小波变换，实现不同振荡特征成分的有效分离。

利用双调Q小波变换分析轴承故障振动信号，即据信号振荡特征，设两不同Q值的小波基函数库分别表示信号中不同振荡成分，并获得相应系数。若准确表示轴承故障振动信号中高、低振荡成分，两个表示不同振荡程度的TQWT基函数库选取非常关键(设Q1

(6)

由两条件可见，在准确表达振荡程度前提下Q1及Q2值相差越大相关系数值越小。然而，相比低Q值TQWT，高Q值TQWT需更多分解层数才能覆盖同样频率范围，需增加分解层数才能提高分辨率。在给定Q值、γ值时(一般取3)时相应最大分解层数已确定，故分解层数J并不能取无穷大，通常取最大值Jmax，即

(7)

式中：N为信号长度；[]为取下舍入值。

为将用高Q值小波表示的持续振荡成分与低Q值小波表示的故障瞬态成分有效分离，需引入形态学成分分析方法，即利用信号组成成分的振荡程度差异性实现不同信号成分分离。

设所测轴承故障振动信号y含高、低振荡成分xH，xL及噪声成分，利用引进方法分离提取低振荡成分即可转化为求解目标函数最优化。

λH‖wH‖1+λL‖wL‖1

(8)

(9)

2仿真分析

用仿真信号进行试验分析，即

x(t)=exp(-445t)sin(980πt)

(10)

采样频率32 kHz，采样时间1 s，调制频率fs=100 Hz，所得仿真信号时域波形见图3(a)；在此信号上叠加方差为0.25的高斯白噪声信号，获得波形见图3(b)。此时信号的信噪比为-6.383 9 dB。由图3看出，瞬态成分被淹没在噪声中。用本文方法处理轴承仿真信号，选高Q值TQWT参数为Q2=7，γ2=3，J2=79；低Q值TQWT参数为Q1=1，γ1=3，J1=20。提取的瞬态成分见图3(c)，并对其进行Hilbert包络分析，获得特征频率见图3(d)，可见已获得明显的调制频率fs=100 Hz，验证了方法的有效性。

图3　仿真信号分析结果 Fig.3 Simulation signal analysis

3滚动轴承故障瞬态成分检测应用

为检验基于双调Q小波变换的瞬态成分提取方法在轴承故障诊断中的应用效果，将该方法用于轴承外圈、滚动体局部故障瞬态成分提取。轴承外圈存在局部故障时，由于滚动体通过外圈故障部位使轴承的振动信号出现周期性初始幅值相同瞬态成分。轴承滚动体存在局部故障时，随滚动体转动瞬态成分幅值呈周期性变化；滚动体自转一周分别与内外圈各接触一次，产生两次冲击，且与外圈接触产生的冲击远大于内圈接触，因此会产生强弱相间的瞬态成分。

选N203型圆柱滚子轴承为实验对象，其物理参数见表。据滚动轴承的故障特征频率与主轴旋转频率及轴承物理结构关系可得外圈及滚动体故障特征频率为

(11)

式中: fo为外圈故障特征频率；fr为滚动体故障特征频率；f为主轴旋转频率；Z为滚动体数目；d为滚动体直径；D为轴承节径；α为接触角。

N203型圆柱滚子轴承故障特征频率见表2。外圈及滚动体故障特征频率分别为fo=117.8 Hz，fr=145.7 Hz。

表1　N203圆柱滚子轴承特征参数

表2　N203圆柱滚子轴承故障特征频率

在滚动轴承外圈及滚动体构造复杂的剥落损伤故障以模拟实际轴承外圈及滚动体故障，见图4。较传统单纯线切割故障设置，该方法构造的轴承故障更接近实际，轴承故障振动信号更复杂，故障瞬态成分提取也更困难。实验设置采样频率32 kHz，采样时间1 s，驱动电机转速设置为1 750 r/min，即主轴转动频率为29.2 Hz。所测轴承外圈及滚动体故障振动信号分别见图5(a)、图9(a)。

图4　N203滚动轴承故障状态 Fig.4 Fault condition of N203 cylindrical rolling bearing

3.1外圈故障瞬态成分检测

图5(a)为滚动轴承外圈剥落故障振动信号，可见故障瞬态成分杂乱，无法判断故障类型。用基于双调Q小波变换的瞬态成分方法提取轴承故障瞬态成分，选高Q值TQWT参数分别为Q2=10，γ2=3，J2=100；低Q值TQWT参数分别为Q1=2，γ1=3，J1=30。提取低振荡故障瞬态成分结果见图5(b)；再进行Hilbert包络分析，获得故障特征频率fo=117.5 Hz，见图5(c)，可见与轴承外圈故障特征频率一致，故可判断轴承外圈发生故障，与实际情况相符，从而验证方法的有效性。

为验证该方法在轴承外圈故障瞬态成分提取的优越性,分别用均值滤波、小波阈值及EMD分析原始轴承外圈故障信号，所得结果见图6～图8。由3图看出，三种方法在提取的轴承外圈故障瞬态成分不及本文方法效果好。本文方法能更有效提取轴承外圈故障瞬态成分，所得外圈故障特征频率更明显。

图5　双调Q小波变换 Fig.5 Double-TQWT method

图6　均值滤波 Fig.6 Average filtering method

图7　小波阈值 Fig.7 Wavelet threshold method

图8　EMD Fig.8 EMD

图9　双调Q小波变换 Fig.9 Double-TQWT method

图10　均值滤波 Fig.10 Average filtering method

图11　小波阈值 Fig.11 Wavelet threshold method

图12　EMD Fig.12 EMD

3.2滚动体故障瞬态成分检测

图9(a)为轴承滚动体故障振动信号，可见从原始故障振动信号中不能直接判断故障类型，用本文方法提取故障瞬态成分，所得结果见图9(b)；再进行Hilbert包络分析，获得故障特征频率fr=143.2 Hz见图9(c)，可见与轴承滚动体故障特征频率一致，故可判断滚动体发生故障，与实际情况相符，验证方法的有效性。

为验证本文方法的优越性，分别利用均值滤波、小波阈值及EMD方法分析滚动体故障原始信号，获得结果分别见图10～图12。由3图可知，与均值滤波、小波阈值及EMD方法相比，本文方法更能有效提取轴承滚动体故障瞬态成分，获得更明显的滚动体故障特征频率，本文方法的优越性得以验证。

4结论

(1)本文提出的基于双调Q小波变换的轴承故障瞬态成分提取方法，据信号振荡特征而非频率特征，通过设定不同Q值的小波基函数，获得高Q值TQWT及低Q值TQWT的基函数库及相应变换系数，再利用形态学成分分析方法，非线性分解出信号中低振荡瞬态成分。

(2)通过对仿真信号、实际轴承外圈及滚动体故障信号分析结果表明，该方法能较好提取轴承故障瞬态成分；较均值滤波、小波阈值及EMD更能有效提取轴承故障瞬态成分，获得更明显的故障特征频率。进一步验证基于双调Q小波变换的瞬态成分提取方法的优越性。

参考文献

[1]王国彪,何正嘉,陈雪峰,等. 机械故障诊断基础研究“何去何从”[J]. 机械工程学报,2013, 49(1)：63-72.

WANG Guo-biao，HE Zheng-jia，CHEN Xue-feng, et al. Basicresearch on machinery fault diagnosis-what is the prescription[J]. Journal of Mechanical Engineering, 2013, 49(1): 63-72.

[2]郝如江,卢文秀,褚福磊.滚动轴承故障信号的数学形态学提取方法[J].中国电机工程学报,2008,28(26):65-70.

HAO Ru-jiang, LU Wen-xiu, CHU Fu-lei. Mathematical morphology extracting method on roller bearing fault signals[J]. Proceedings of the CSEE, 2008, 28(26): 65-70.

[3]王诗彬，许佳，朱忠奎. 瞬态成分参数的最小二乘法辨识及其轴承故障特征提取应用[J].机械工程学报，2014, 48(7): 68-76.

WANG Shi-bin, XU Jia, ZHU Zhong-kui. LSM-based transient parameter identification and its application in feature extraction of bearing fault[J].Journal of Mechanical Engineering, 2014, 48(7): 68-76.

[4]He Qing-bo, Du Ru-xu. Mechanical watch signature analysis based on wavelet decomposition[J]. International Journal of Wavelets, Multiresolution and Information Processing, 2009, 7(4): 491-512.

[5]Wang Shi-bin, Huang Wei-guo, Zhu Zhong-kui. Transient modeling and parameter identification based on wavelet and correlation filtering for rotating machine fault diagnosis[J]. Mechanical Systems and Signal Processing, 2011, 25(4): 1299-1320.

[6]Yan R Q, Gao R X. An efficient approach to machine health diagnosis based on harmonic wavelet packet transform[J]. Robotics and Computer-Integrated Manufacturing, 2005,21(4):291-301.

[7]Cao Hong-rui, Lei Ya-guo, He Zheng-jia. Chatter identification in end milling process using wavelet packets and Hilbert-Huang transform[J].International Journal of Machine Tools and Manufacture, 2013, 69:11-19.

[8]Selesnick I W.Wavelet transform with tunable Q-factor [J]. Ieee Transaction Signal Processing, 2011, 59(8): 3560-3575.

[9]Cai Gai-gai, Chen Xue-feng, He Zheng-jia. Sparsity- enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox[J]. Mechanical Systems and Signal Processing, 2013, 41(1/2): 34-53.

[10]Selesnick I W. Resonance-based signal decomposition: a new sparsity-enabled signal analysis method[J]. Signal Processing, 2011, 91 (12): 2793-2809 .

[11]唐进元，陈维涛，陈思雨,等.一种新的小波阈值函数及其在振动信号去噪分析中的应用[J]. 振动与冲击，2009, 28(7): 118-121.

TANG Jin-yuan, CHEN Wei-tao, CHEN Si-yu, et al. Wavelet-based vibration signal denoising with a new adaptive thresholding function[J]. Journal of Vibration and Shock, 2009, 28(7): 118-121.

[12]沈长青,谢伟达,朱忠奎,等.基于EEMD和改进的形态滤波方法的轴承故障诊断研究[J].振动与冲击, 2013, 32(2)：39-43.

SHEN Chang-qing, XIE Wei-da, ZHU Zhong-kui,et al. Rolling element bearing fault diagnosis based on EEMD and improved morphological filtering method[J]. Journal of Vibration and Shock , 2013, 32(2): 39-43.