水平双向地震激励下基于序列最优控制算法曲线梁桥控制分析

第一作者李喜梅女，博士生，1979年生

通信作者杜永峰男，教授，博士生导师，1962年生

水平双向地震激励下基于序列最优控制算法曲线梁桥控制分析

李喜梅1,2，杜永峰1,2(1．兰州理工大学西部土木工程防灾减灾教育部工程研究中心，兰州730050；2.兰州理工大学防震减灾研究所，兰州730050)

摘要：针对曲线梁桥在地震作用下出现的平扭耦合作用对结构产生的不利影响，将隔震技术与附加减震装置相结合对平扭耦合进行控制。建立考虑上部结构偏心的曲线梁桥在双向水平地震作用下的振动控制方程，分别采用序列最优控制算法(Sequential Optimal Control,SOC)及经典线性最优控制(Classical linear Optimal Control,COC)对结构进行分析，求解曲线桥两种控制算法的地震响应，并通过比较研究两种控制算法的适用性。结果表明，序列最优控制算法较经典线性最优控制能更有效减小曲线梁桥在水平双向地震作用下的地震反应、抑制结构扭转耦合效应，对减少落梁震害、确保曲线桥抗震安全有较好的工程实用价值。

关键词：曲线桥；双向地震激励；最优序列控制

基金项目：国家自然科学基金资助项目(51178211)

收稿日期：2014-02-10修改稿收到日期：2014-05-09

中图分类号:TU352.1；U441+.3文献标志码：A

Curved girder bridges’ control based on sequential optimal control algorithm under two-directional horizontal earthquake

LIXi-mei1,2,DUYong-feng1,2(1. MOE Western Engineering Research Center of Disaster Mitigation in Civil Engineering， Lanzhou Univ. of Tech.， Lanzhou 730050，China；2. Institute of Earthquake Protection and Disaster Mitigation, Lanzhou Univ. of Tech., Lanzhou 730050, China)

Abstract:Translation-torsion coupling action of curved girder bridges causes adverse effects on structures under earthquake action. Here, the seismic isolation technique and additional damping device were combined to control the translation-torsion coupling of curved girder bridges. The equations of motion for curved girder bridges considering their upper structure’s eccentricity under two-directional horizontal earthquake were established, the sequential optimal control (SOC) and classical linear optimal control (COC) were used to solve the seismic responses of curved girder bridges. The results indicated that the SOC method can more effectively reduce the seismic responses of curved beam bridges under two-directional earthquake and suppress the translation-torsion coupling effects than the COC method can. The study results were valuable for reducing seiamic damage of falling girders and ensuring aseismic safety of curved girder bridges.

Key words:curved bridges; two-directional horizontal earthquake; sequential optimal control (SOC)

曲线梁桥已发展为大中城市最便捷、直接的交通要道及枢纽[1]。对普通直线桥梁已有多种减、隔震控制方法，但对曲线桥的减、隔震研究较少。主动控制中控制算法为关键步骤，而半主动控制算法往往可基于主动控制算法导出，因此研究主动控制算法有重要意义[2]。亓兴军等[3-5]采用经典最优控制算法对曲线连续梁桥建立有限元在三维地震动下控制效果进行分析，但计算过程需求解非线性Riccati方程，有限元模型自由度数量太多导致求解严重困难。阎石等[6-9]对曲线梁桥的振动控制研究未考虑地震波水平双向输入。而对曲线桥而言，由于结构本身不规则性，会造成纵、横向地面运动相互耦合，故应考虑地震动两水平分量同时作用情况。杜永峰等[10]针对经典最优控制算法缺点，借鉴离散系统最优控制的Bellman最优法则，在每个时间步长上建立目标函数，导出更一般的序列最优控制算法(SOC)，并用于隔震曲线梁桥的控制分析。本文据曲线梁桥受力特点，考虑隔震曲线梁桥上部结构刚度中心与质量中心不一致造成的平扭耦合地震效应，建立隔震曲线梁桥的双质点6自由度简化分析模型，采用序列最优控制算法(SOC)对一座三跨隔震曲线连续梁桥进行分析，并与经典控制算法对比。

1模型建立

1.1模型假设

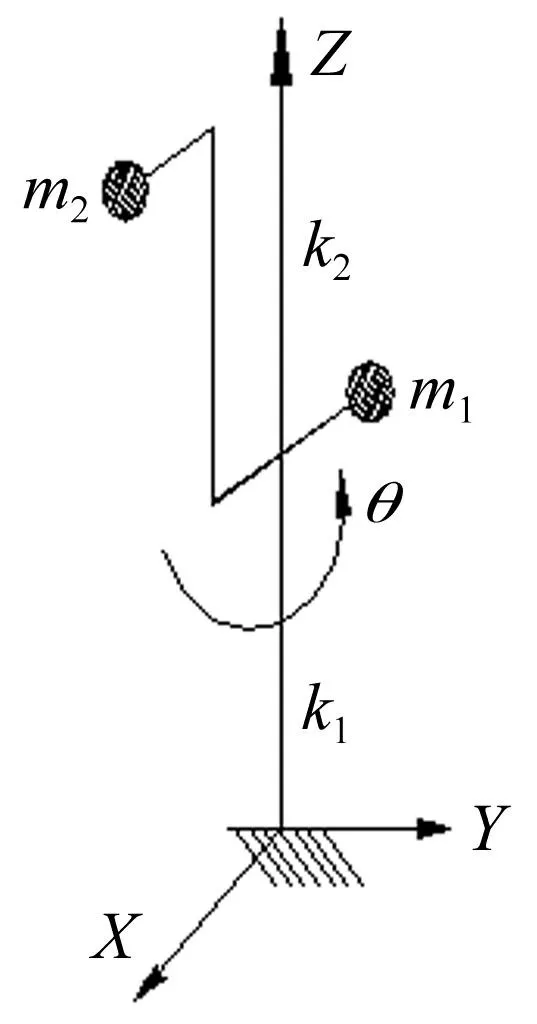
图1　曲线梁桥计算模型简图 Fig.1 Curved bridge deck model

分别将隔震曲线梁桥桥墩及上部结构简化为两个各具两水平x、y自由度与一个围绕质量中心轴扭转θ自由度的堆积质量m1、m2模型系统，桥墩与上部结构为两质点非同轴质量偏心结构的分析模型，上下质点分别表示曲线桥下、上结构，见图1。

1.2运动方程建立

取曲线桥上部结构质量中心为坐标原点，曲线梁桥动力方程可表示为

(1)

式中：m1，m2分别为下、上部结构质量；J1，J2分别为下、上部结构转动惯量[11]；ri为回转半径；Xmi、Ymi分别为下、上部结构质心相对于参考轴坐标；Kxx，Kyy分别为结构在x、y向平动刚度，取隔震桥梁结构为剪切型，Kxθ，Kyθ分别为结构x、y向平扭刚度，考虑上、下部结构质心与刚心的偏心距及上、下部结构质心间偏心距，Kθθ为结构的扭转刚度矩阵。

Kθx=KxθT，Kθy=KyθT

式中：Kx1，Ky1与Kx2，Ky2分别为下、上部结构平移刚度；Kxθ12，Kyθ12分别为仅m2发生x、y向单位位移时m1需施加的绕z轴力矩；Kθθ12为m1不动仅m2发生单位转角时m1需施加的绕z轴力矩；Kxθ11，Kxθ22,Kxθ21，Kyθ11，Kyθ22,Kyθ21，Kθθ11，Kθθ22,Kθθ21含义以此类推[12-13]。

阻尼矩阵[C]用分区瑞利阻尼模型可分解为

[C]=[C0]+[Cr]，(C0)=αs[M]+βs[K]

式中：[Cr]为体现非比例阻尼的余项阻尼矩阵；Cbr=(αb-αs)mb+(βb-βs)kb；[C0]为经典瑞利阻尼矩阵；αs，βs，αb，βb分别为下部结构及隔震系统瑞利阻尼比例系数,即

式中：ξs，ξb分别为下部结构及隔震系统瑞利阻尼比例系数；ωi、ωj为结构第i,j阶圆频率。

将式(1)转化成状态空间表达式，即

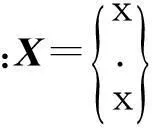
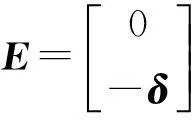
2基于状态反馈的序列最优控制算法

时域内结构最优控制算法大多对问题进行简化，文献[14-16]中序列最优控制算法吸收了几种常见算法优点，并对现有算法进行改进，将控制目标函数化解至每个时间步长，导出更一般的最优控制算法，并用状态转移的数值方法实现。

2.1基于序列最优控制目标函数的最优控制力模型

据状态反馈序列最优控制算法构造双向地震作用下二次型控制目标函数为

(2)

式中：{X(t)}为含x，y两方向的结构响应；[Q]，[R]分别为对应两方向响应及控制力的权重矩阵；t0，tf分别为控制起止时刻。

将地震波及控制力转化为一系列时间域脉冲，由于地震动及控制力均随时间推移逐步输入至结构系统，则系统当前时刻响应由当前时刻脉冲与过去时刻脉冲响应叠加而成，即

{X(t)}={X∑(j-1)(t)}+{Xj(t)}

(3)

式中：下标“∑(j-1)”代表直到第(j-1)个步长上(过去时刻)脉冲影响总和。

将式(3)代入式(2)构造Lagrange函数，原约束优化问题转化为无约束问题。因当前时刻脉冲只影响当前时刻及未来时刻响应，对过去时刻响应无影响，因此将纯粹含过去时刻脉冲影响控制目标函数分离，引用最优控制理论的泛函极值条件，可得结构最优控制的一般表达式为

{fc(tA)}=-[R]-1[B]T{λ(tA)}

(4)

(5)

(6)

式中：tA为当前时刻，式(5)、(6)定义域为[tA,tf]。

2.2基于状态反馈的序列最优控制算法实现

在式(5)中直接求解{λ}，利用状态转移算法得

(7)

利用状态转移算法，由式(6)建立递推公式为

式中：m为终了时刻时间步长数。

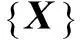
(9)

式(7)中取k=m，引入终值条件λ(tA+mΔt)=0，将式(9)代入式(7)并反复逆向递推，最终得

{λ(tA)}=-Δt[QA(m)]({X(tA)}+

(10)

[QA(m)]=e-[Aλ]mΔt [Qλ]e[A]mΔt+

e-[Aλ](m-1)Δt [Qλ]e[A](m-1)Δt+…+

e-[Aλ]Δt [Qλ]e[A]Δt

(11)

将式(11)代入式(4)可求得状态反馈时距控制终了时刻m个时间步长对应的理想控制力，即

{fc(tA)}=Δt[IRX(m)]{X(tA)}+

(12)

式中：

[IRX(m)]=[IQ(m)]-1[RQ(m)]

{ERX(m)}=[IRX(m)]{E}

[IQ(m)]=[I]-(Δt)2[RQ(m)][B]

[RQ(m)]=[R]-1[B]T[QA(m)]

式中：IRX(m)，ERX(m)为最优控制力系数，可由此求出每个时刻的最优控制力。

较经典最优控制算法，序列最优算法在求解过程中未对目标函数预先引用近似简化条件，除将地震波转化为一系列脉冲、采用状态转移数值算法本身误差外，该算法建立的模型在概念上更精确。

3隔震曲线连续梁桥算例及讨论

3.1工程背景

某立交匝道上一联圆曲线连续梁桥，跨径3×20 m，曲率半径R=50 m，圆心角θ=69°，主梁为单箱单室箱梁。为简化分析，用独柱式圆形桥墩，直径1.5 m，墩高5 m，墩底固结，每个墩顶布置圆形铅芯橡胶支座。下部结构阻尼比ξs=0.05，隔震层水平阻尼比ξb=0.15，上部结构质心为整体坐标系原点。曲线桥梁有限元模型由107个节点、106个单元组成。平面布置及有限元模型见图2。

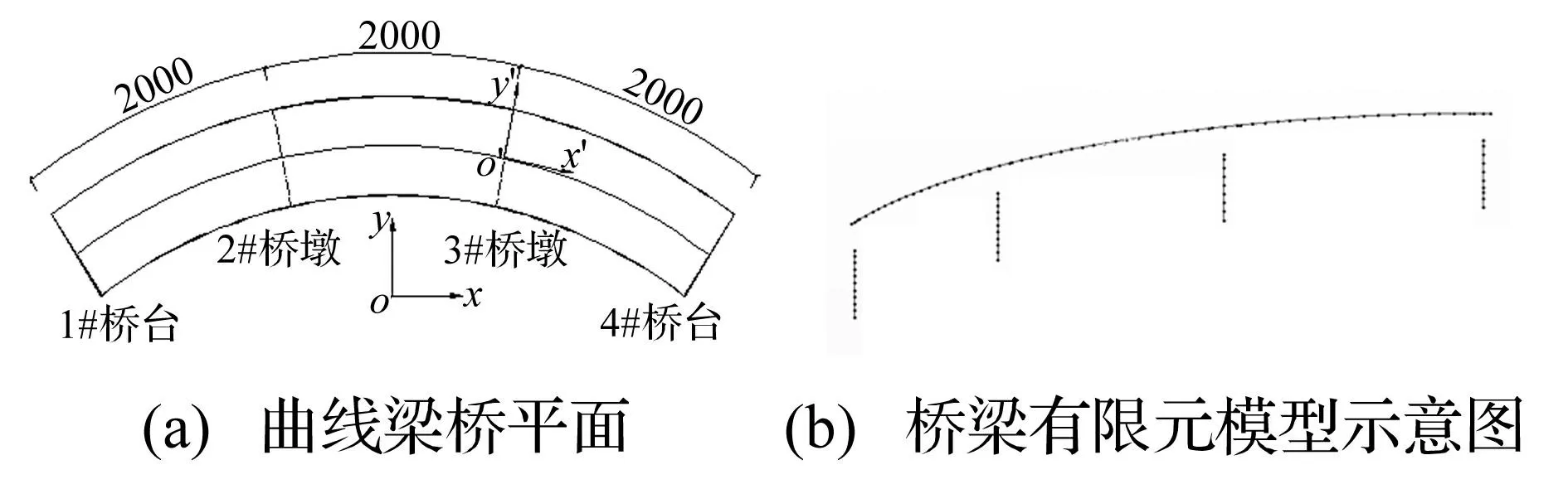
图2　曲线梁桥布置图 Fig.2 Curved bridge layout

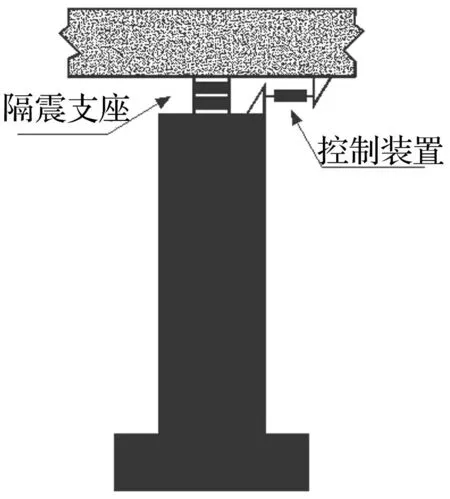
图3　径向、切向阻尼 器布置示意图 Fig.3 The dampers arrangement for radial and tangential

每个桥墩处切向、径向各设置一组理想智能控制器连接墩台与主梁，最大阻尼力2 000 kN，见图3。采用状态反馈序列最优控算法对结构进行控制，设控制器能实时提供所需控制力，且不计时滞及自身动力效应。地震激励采用常用的3种地震波进行分析，在结构x向、y向分别同时输入El-Centro、Kobe及Northridge地震波南北及东西分量。为比较方便，加速度峰值x方向调整为250 cm/s2，y方向调整为220 cm/s2，分别求隔震曲线梁桥在无、有控状态下的地震响应。

3.2控制效果分析

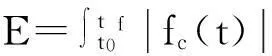
3图看出，或El-Centro地震波，或Kobe、Northridge地震波，推导的序列最优控制算法(SOC)与经典线性最优控制(COC)消减曲线桥结构位移响应作用相当，而序列最优控制算法(SOC)更有效。因此对总体控制效果而言，序列最优控制算法优于经典最优控制算法。如输入El-Centro地震波，由图4可知上部结构x、y向最大位移控制率分别为51.7%及38.3%，且不仅最大值减小，在时程几乎所有时刻均有不同程度减小。

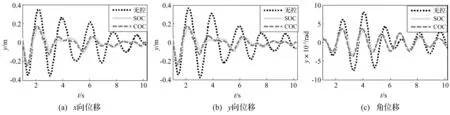
图4　输入El-Centro波上部结构位移时程图 Fig.4 Displacement of superstructure under El-Centro

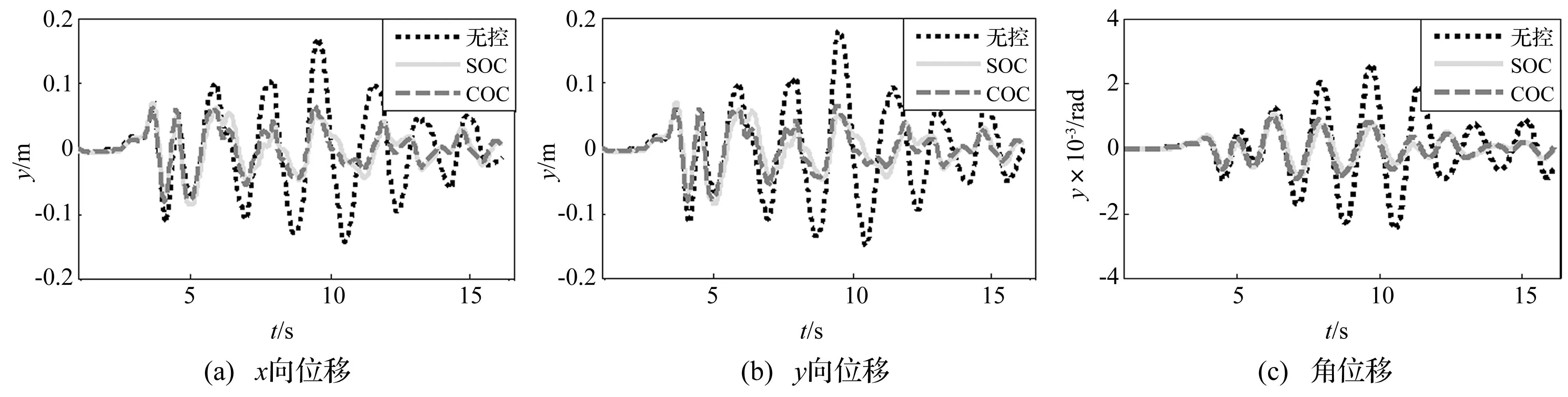
图5　输入Kobe波上部结构位移时程曲线 Fig.5 Displacement of superstructure under Kobe

图6　输入Northridge波上部结构位移时程曲线 Fig.6 Displacement of superstructure under Northridge

输入El-Centro波、Kobe波、Northridge波下上部结构的x、y向及扭转角加速度控制时程曲线见图7～图9。由3图看出，或El-Centro地震波，或Kobe、Northridge地震波，在同等控制能量条件下推导的序列最优控制算法(SOC)消减结构最大峰值加速度及结构扭转角加速度效果较经典线性最优控制(COC)均更有效。在Kobe地震动初期加速度反应值有局部放大现象，因原结构施加控制力或添加控制装置后会改变结构动力特性，部分时间点加速度可能增大，但大部分时间点加速度均会减小，能达减震控制目的。

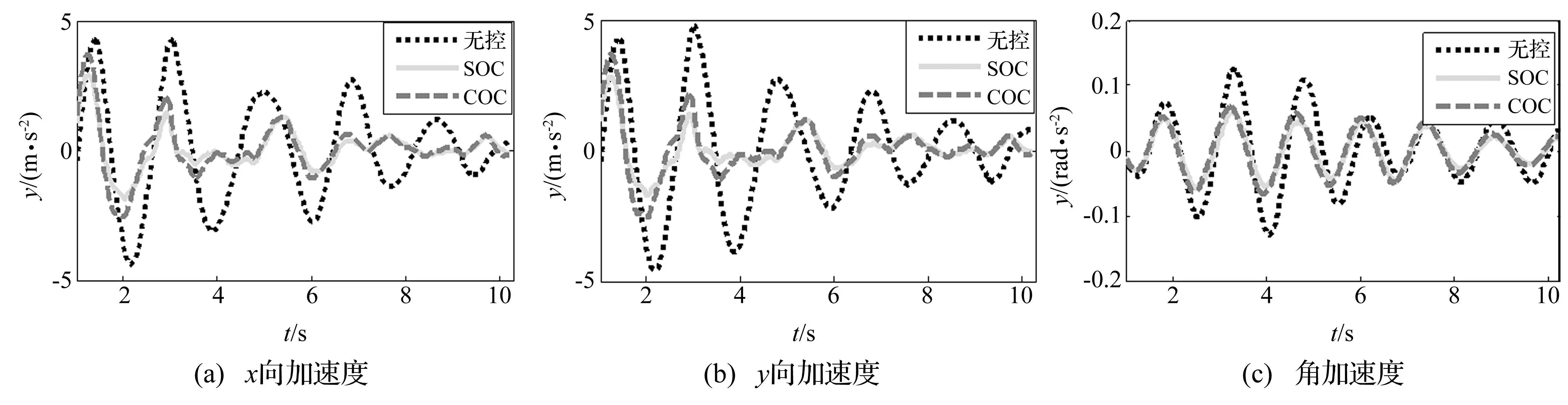
图7　输入El-Centro波上部结构绝对加速度时程曲线 Fig.7 Superstructure absolute acceleration under El-Centro

图8　输入Kobe波上部结构绝对加速度时程曲线 Fig.8 Superstructure absolute acceleration under Kobe

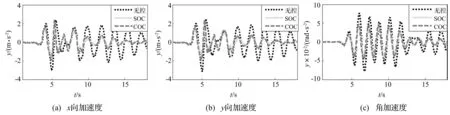
图9　输Northridg波上部结构绝对加速度时程曲线 Fig. 9 Superstructureabsolute acceleration under Northridg

曲线梁桥在El-Centro波输入下，无控、序列最优控制算法(SOC)及经典线性最优控制(COC)三种不同控制策略响应最大值见表1。由表1看出，两种控制算法控制效果均较好，但在相同能量指标下，序列最优控制算法(SOC)位移、加速度最大值较经典线性最优控制(COC)小，控制效果更明显。在Kobe、Northridge地震波作用下，规律相同。

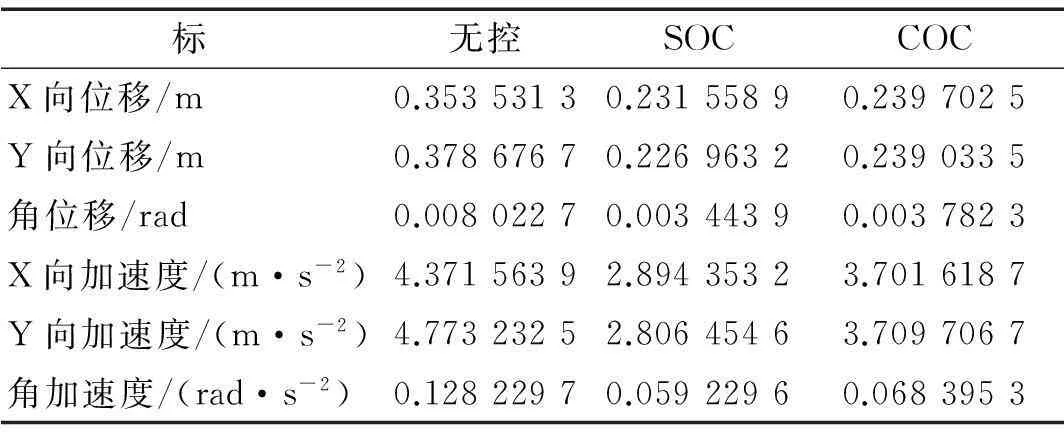
表1　El-Centro波下不同控制策略响应最大值

由于墩顶共布置8 个控制器，分析单个控制器的控制力大小对比较两种算法控制效率意义不大。因此分别将布置在径向与切向4个控制器的控制力迭加，获得x、y向控制力合力时程。结构在同等控制能量条件下El-Centro波输入的x、y向控制力合力时程曲线见图10。由图10看出，在时程曲线开始段，序列最优控制算法(SOC)控制力高于经典线性最优控制(COC)，而在时程曲线尾部序列最优控制算法(SOC)控制力低于经典线性最优控制(COC)。故序列最优控制算法(SOC)所得控制力幅值随结构响应衰减快速减小，在地震动峰值较大阶段能更好发挥控制效果。

图10　输入El-Centro波控制力时程曲线 Fig.10 The control force of time-history curve under El-Centro

4结论

曲线桥因受偏心及多维地震动作用，使结构反应表现出平动、转动的耦联效应。本文考虑曲线桥的偏心及多维地震动输入，通过序列最优控制算法(SOC)，对曲线桥地震反应进行控制分析，结论如下：

(1)本文所用序列最优控制算法无需求解Riccati方程，计算量小，未预先对目标函数引用近似简化，仅将地震波转化为一系列脉冲及采用状态转移的数值算法本身误差外，本算法在概念上更合理。

(2)采用序列最优控制算法(SOC)使上部结构角加速度响应及扭转角位移响应均得到显著减小，由因曲线桥偏心引起的扭转响应得以降低，并使上部结构x、y向位移及加速度响应得到有效控制。

(3)同等控制能量条件下，序列最优控制算法(SOC)在时程曲线尾部可降低控制力输入、节约输入能量。因此SOC控制效能更高。

参考文献

[1]孙广华. 曲线梁桥计算[M]. 北京：人民交通出版社,1997.

[2]李宏男,李忠献,祁皑. 结构振动与控制[M]. 北京: 中国建筑工业出版社, 2005.

那么推什么？一言以蔽之，就是推进廉洁政治建设。干部清正、政府清廉、政治清明，是习近平总书记推进反腐倡廉建设思想的目标和理念。干部清正，不仅仅对执政党自身的建设和国家政权体系的建设有利，更是对整个社会风气的健康发展有重要作用。清廉是共产党领导的人民政府应有的本质特征。政治清明，是社会主义国家的内在要求。中国共产党领导广大人民群众进行民主政治建设，理应是清明的政治。

[3]亓兴军, 申永刚. 三维地震动作用下曲线连续梁桥减震控制研究[J]. 振动与冲击, 2012, 31(6): 119-125.

QI Xing-jun,SHEN Yong-gang. Seismic mitigation control for a curved continuous girder bridge with 3-D ground motion action[J]. Journal of Vibration and Shock, 2012, 31(6): 119-125.

[4]亓兴军,李小军,唐晖. 曲线桥弯扭耦合减震半主动控制分析[J]. 公路交通科技, 2006, 23(9): 54-57.

QI Xing-jun, LI Xiao-jun, TANG Hui. Study on semi-active control of seismic bend torsion coupling for curved bridge[J]. Journal of Highway and Transportation Research and Development, 2006, 23(9): 54-57.

[5]全伟,李宏男. 曲线桥多维多点地震激励半主动控制分析[J]. 工程力学, 2009,26 (3): 79-85.

QUAN Wei , LI Hong-nan.Semi-active control of curved bridge under multi-component and multi-support earthquake [J]. Engineering Mechanics, 2009,26 (3): 79-85.

[6]阎石, 张海. 高架桥地震反应半主动控制分析[J]. 地震程与工程振动, 2003, 23(6): 169-173.

[7]陈水生. 高架桥梁地震响应磁流变阻尼器(MR)半主动控制[J]. 长安大学学报(自然科学版), 2003,23(6): 40-43.

CHEN Shui-sheng.Magneto-rheological(MR) dampers semi-active control of earthquake response for elevated bridge[J]. Journal of Chang`an University(Natural Science Edition), 2003,23(6): 40-43.

[8]李忠献,岳福清. 城市隔震高架桥地震反应的半主动控制[J].土木工程学报,2007,40(1):42-48.

LI Zhong-xian, YUE Fu-qing, Semi-active control on seismic responses of vibr ation-insulated urban elevated br idges[J]. China Civil Engineering Journal, 2007,40(1):42-48.

[9]陈送财,李锦华. 高架桥地震响应的半主动控制研究[J].合肥工业大学学报(自然科学版),2010.33(7):1053-1056.

CHEN Song-cai,LI Jin-hua. Semi-active control on seismic responses of elevated highway bridges[J]. Journal of Hefei University of Technology(Natural Science), 2010,33(7): 1053-1056.

[10]杜永峰,刘彦辉,李慧. 双向偏心结构扭转耦联地震反应的序列最优控制[J]. 地震工程与工程振动,2007,27(4):133-138.

DU Yong-feng,LIU Yan-hui,LI Hui.Sequential optimal control of torsional coupled seismic response for bidirectionally eccentric structure [J]. Journal of Earthquake Engineering and Engineering Vibration,2007,27(4): 133-138.

[11]李宏男,霍林生. 结构多维减震控制[M].北京:科学技术出版社,2008.

[12]王丽,周锡元,闫维明. 曲线梁桥地震响应的简化分析方法[J].工程力学,2006,23(6): 77-84.

WANG Li,ZHOU Xi-yuan,YAN Wei-ming. Simplified analysis method for seismic response of curved bridges[J]. Engineering Echanics,2006,23(6): 77-84.

[13]党育. 复杂隔震结构的分析与软件实现[D]. 武汉:武汉理工大学, 2011.

[14]杜永峰. 被动与智能隔震结构地震响应分析及控制算法[D].大连：大连理工大学,2003.

[15]Chi Y, Sain M K, Pham K D, et al. Structural control paradigms for an asymmetric building[C]. Proceedings of the 8th ASCE Special Conference on Probabilistic Mechanics and Structural Reliability, 2000:152.

[16]杜永峰,李慧,赵国藩. 地震作用下结构振动最优控制的一种一般算法[J].大连理工大学学报,2004,44(6):864-869.

DU Yong-feng, LI Hui, ZHAO Guo-fan. a general algorithm of the structure vibration optimal control of seismic excitations[J]. Journal of Dalian University of Technology, 2004, 44(6):864-869.