基于单位四元数的单独像对相对定向

基于单位四元数的单独像对相对定向

柳建锋,盛庆红,王惠南

(南京航空航天大学航天学院，江苏南京210016)

摘要：目前对单位四元数描述空间旋转的应用，基本上是将其转换成旋转矩阵的形式，而忽略了单位四元数描述空间向量旋转具有描述几何关系的直观性以及运算简洁的优势。基于此提出一种基于单位四元数的单独像对相对定向法，方法首先采用向量描述同名光线，然后利用单位四元数描述立体像对中左右影像同名光线的变换关系，建立单位四元数共面条件方程模型，再按照带有约束条件的间接平差原理进行最小二乘平差，确定相对定向元素。针对RC30航空影像和低空无人机影像采用单位四元数法分别进行单独像对相对定向实验，结果表明单位四元数相对定向方法计算精度较高,为解决摄影测量中坐标变换问题提供更多选择。

关键词：单独像对相对定向；单位四元数；共面条件方程；欧拉角

中图分类号：P23

收稿日期：2014-10-30

基金项目：国家自然科学基金资助项目(41471381；41101441);南京航空航天大学研究生创新基地开放基金项目(kfjj130133)

作者简介：柳建锋(1990-)，男，硕士研究生.

Independent relative orientation based on unit quaternion

LIU Jian-feng,SHENG Qing-hong,WANG Hui-nan

(College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016,China)

Abstract：The main method of describing spatial rotation with unit quaternion is rotation matrix,without considering property of unit quaternion.Unit quaternion can intuitively and succinctly describe rotation of vectors.Based on this,an innovative method in the independent relative orientation based on unit quaternion is proposed.The algorithm describes corresponding image rays as vectors，then uses unit quaternion to describe the rotational relationship of corresponding image rays.Coplanarity condition equation is linearized by the eight elements of two unit quaternion and elements of relative orientation and calculated using an iterative method according to indirect adjustment with constraints.The relative orientation of RC30 aerial images and UAV images are realized with method unit quaternion and method Euler angles.The results show that the relative orientation accuracy of the method unit quaternion is better than method Euler angle.It provides more options to solve the problems of coordinate transformation in photogrammetry.

Key words：independent relative orientation;unit quaternion;coplanarity condition equation；Euler angles

立体像对的相对定向是摄影测量学的基础，相对定向在三维重建技术、数字影像三维可视化研究以及高精度定位等方面发挥着重要作用[1]。如何有效精准地描述左右影像像空间辅助坐标系之间的关系是相对定向中的关键问题。基于多种同名特征的相对定向法[2]和基于广义点的相对定向[3]，从获取高精度匹配点的角度出发，提高定向精度。附有四个独立约束条件的相对定向法[4]，将约束条件加入到解决过度参数化的求解中，计算结果更加稳定可靠。利用IMU/GPS信息作为外方位元素先验值加入到相对定向的平差中[5]，有效降低匹配误差对于定向结果的影响，提高定向元素解算的精准度。以上相对定向方法在描述坐标系转换关系时主要利用欧拉角法，求解过程中存在着复杂的三角运算，运算量大而且求解时可能会导致溢出。单位四元数可以方便的构建旋转矩阵，而且可以实现姿态描述的唯一性，已广泛应用于导航[6]和飞行器姿态确定等领域[7]。在摄影测量学中单位四元数也已经成功应用于构建共线条件方程[8]、线阵CCD影像的外方位元素解算[9]以及空间后方交会[10]、三维空间相似变换解算[11]、连续像对相对定向[12]中。

但上述单位四元数的应用只是将旋转矩阵用单位四元数的元素来表示，与欧拉角唯一区别仅仅在于参数的选择不同，并没有体现出单位四元数描述空间向量旋转的几何关系的直观性以及其运算简洁的优势[13]。本文利用四元数对向量进行代数表示，利用单位四元数描述向量的空间旋转，建立基于单位四元数的共面条件方程模型，解算相对定向元素。

1单位四元数共面条件方程

1.1单位四元数空间旋转

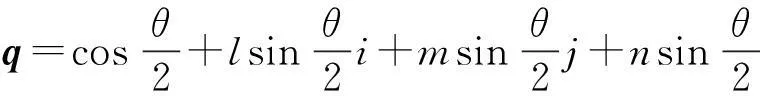
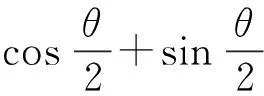
图1　单位四元数空间旋转示意图

(1)式中：n=(l,m,n)表示旋转轴的单位向量;θ表示绕定轴旋转的角度。将空间中的某一点看成是原点指向该点的向量，记为P(x，y，z)T，旋转后得到的点记为P′ (x′，y′，z′)T，那么单位四元数表示的空间旋转过程如图1所示，用数学公式描述为

(2)其中，首先要将三维向量表示成第一个量为零的四元数的形式，然后按照四元数的乘法进行运算。为了方便计算，将P′，P，q表示成矩阵形式

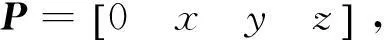
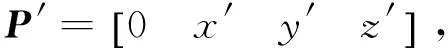
(3)四元数乘法运算法则为pq=[p1q1-p2q2-p3q3-p4q4,

p1q2+p2q1+p3q4-p4q3,

p1q3-p2q4+p3q1+p4q2,

p1q4+p2q3-p3q2+p4q1].

(4)

1.2单位四元数共面条件

图2表示一个立体像对实现单位四元数单独像对相对定向的过程，S1-x1y1z1和S2-x2y2z2分别为立体像对左右影像的像空间坐标，S1-X1Y1Z1和S2-X2Y2Z2分别为左右影像的像空间辅助坐标系，S1m1，S2m2表示一对同名光线，单独像对相对定向的过程即为将所有的同名光线分别绕各自的投影中心旋转，使得它们与空间基线S1S2共面。假设同名像点m1和m2的像平面坐标分别为 (xl,yl)和(xr,yr)，焦距为f，ql和qr为单位四元数，用于分别描述左右影像同名光线向量的坐标变换[14]，记为

(5)那么根据式(2)可以得到m1和m2的像空间辅助坐标，即同名光线S1m1与S2m2的向量为

(6)由于四元数乘法不满足乘法交换律，所以式中参数均按照式(4)的乘法公式从左至右运算。根据式(6)，共面条件方程为

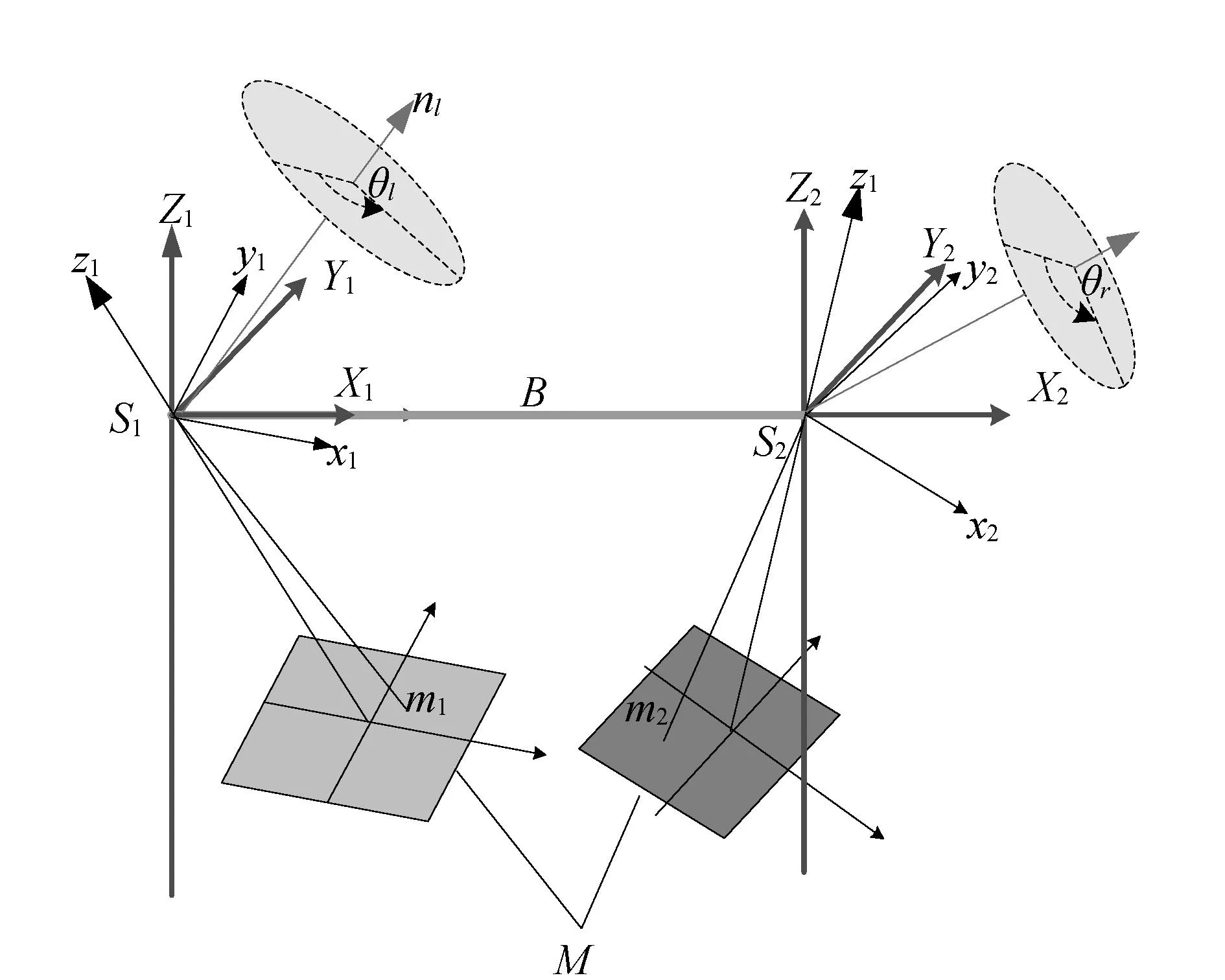
图2　单位四元数共面条件方程模型

(7)目前，对单位四元数的应用主要为将单位四元数转换为旋转矩阵，具体形式如下：

(8)

将式(6)与式(8)比较，可以看出单位四元数与向量的直接运算代替旋转矩阵，在形式上更加简洁，运算更为方便。结合图2可以看出，利用单位四元数代替旋转矩阵，引入的旋转轴和旋转角，可以将光线向量的空间旋转的几何直观性体现出来。

2平差模型及其解算

2.1线性化模型

利用式(4)与式(6)，将式(7)展开，并将等式两边对B归一化处理，然后进行线性化，得到误差方程式为

v=a1dql0+a2dql1+a3dql2+a4dql3+a5dqr0+

(9)

式中，dql0,dql1,dql2,dql3,dqr0,dqr1,dqr2,dqr3为未知数的改正数，其中

F0=YlZr-YrZl.

2.2单独像对相对定向平差计算

将误差方程式V写成矩阵形式为

V=AX+F0.

(10)

其中，

X=

ql和qr是单位四元数，V存在两个约束条件：

(11)

由于单独像对相对定向左影像的ω1=0，则V还存在一个约束条件：

(12)

对式(11)和式(12)进行线性化，可得到约束条件方程

(13)

式中:

令

式(13)矩阵形式为

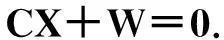
(14)

设观测n对同名点，则对每对同名点按照式(10)可列一个误差方程，则整体平差的误差方程式为

(15)

式中：V和F0是n×1维矩阵，A是n×8维矩阵。采用联系数的直接法[16]，得

(16)

式中

当选取的同名点数量n≥5时，给定ql和qr的初始值，然后解算相对定向元素的改正数，再根据式(16)逐步迭代,直到改正数小于规定的限差终止。

2.3精度评定

单独像对相对定向的相对定向元素φ1，κ1，φ2，ω2，κ2是各未知数的非线性函数。根据协方差传播律[17]，可以计算相对定向元素的精度。记φ1，κ1，φ2，ω2，κ2的协方差阵为DXX，有

(17)

式中，N11=(ATA)-1为8×8的方阵，其主对角线上的元素分别对应着各未知数的权倒数，

式中，

3实验结果与分析

由于相对定向主要用于航空摄影测量，为了验证基于单位四元数的单独像对相对定向算法的正确性、有效性和适用性,本文采用RC30航空影像与低空无人机影像分别进行实验验证。单位四元数的初值设置如下：ql0=qr0=1，ql1=ql2=ql3=qr1=qr2=qr3=0。

RC30航空影像，其航向重叠度为60%，影像的像元大小为0.045mm，内方位元素x0=-0.004mm、y0=-0.008mm、f=152.72mm，影像分辨率5 120×5 120，航高2 290m。实验中，人工选取21对同名点，其分布如图3所示。

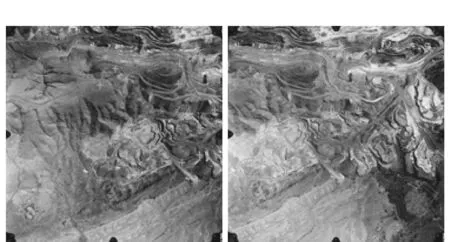
图3　RC30航空影像和特征点

无人机数据为某地区无人机影像，其航向重叠度70%，影像的像素大小为0.006 4mm，影像内方位元素x0=-0.05mm、y0=-0.087mm、f=48.1mm，影像分辨率7 264×5 440，航高700m。实验选取20对同名像点，分布情况如图4所示。

图4　无人机影像和特征点

利用本文方法进行实验，定向结果如表1所示，定向精度如表2所示。

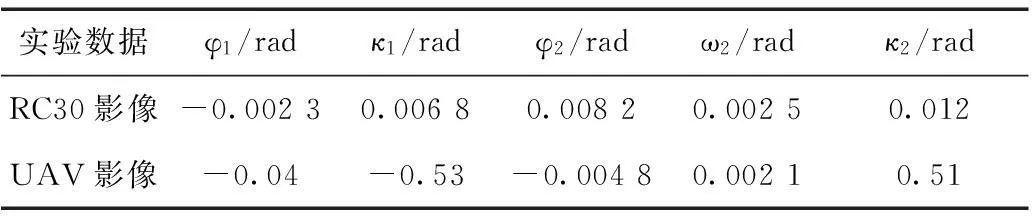
表1　相对定向结果

从表1可以看出，本文采用的单位四元数法能够实现RC30航空影像与低空无人机影像的相对定向，而据相对定向结果可以看出，RC30航空影像相对定向元素值较小，这是由于其平台稳定导致相邻影像相对姿态相差不大；而无人机影像相对定向元素相对偏大，这是由于其平台受外界影响较大，导致相邻影像间相对姿态差别较大。

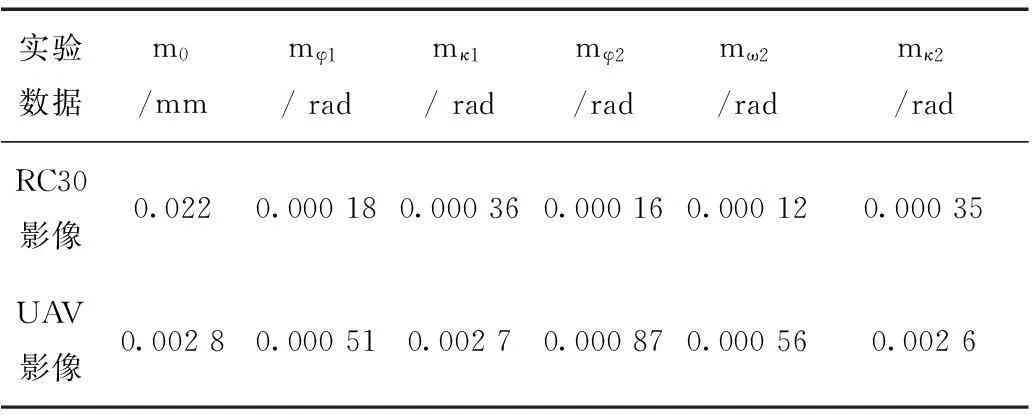
表2　相对定向精度

从表2可以看出，RC30航空影像单独像对相对定向单位权中误差约为0.022 mm(0.5个像素)左右，各未知数中误差也完全合理，验证算法的正确性。无人机影像中误差0.008 3 mm(1.3个像素)，中误差相对偏大，这是由于无人机平台的不稳定导致无人机影像存在一定的形变导致，各相对定向元素精度也在比较合理范围之内。

4结论

单位四元数描述的旋转过程，大多停留在将其转换为旋转矩阵的形式，而忽略单位四元数与向量直接运算在几何意义上的直观与形式上的简洁。本文利用单位四元数与向量直接运算的特点，摒弃旋转矩阵，采用单位四元数与向量的直接运算建立单位四元数单独像对相对定向模型，首先用向量描述同名光线，并将向量扩展为四元数的形式，然后采用单位四元数来描述同名光线的旋转关系，根据同名光线相交原理建立共面方程，求解相对定向元素。结果表明文中采用的方法形式简洁，同时还验证了文中相对定向方法对多种航空影像的可靠性，为今后越来越多的轻小平台影像的相对定向提出一种新思路，为摄影测量中涉及到坐标变换的问题提供更多的选择性。如何发掘单位四元数法在摄影测量以及其他更多领域中的潜能和更多的优势将成为接下来要研究的内容。

参考文献：

[1]张剑清，潘励，王树根.摄影测量学[M].武汉:武汉大学出版社，2009.

[2]ZHANG Y,HU B,ZHANG J.Relative orientation based on multi-features [J].ISPRS Journal of Photogrammetry and Remote Sensing,2011,66(5)：700-707.

[3]何乔，赵泳，张保明,等.基于广义点的相对定向和绝对定向[J].海洋测绘，2006,26(4)：24-26.

[4]ZHANG Y,HUANG X,HU X,et al.Direct relative orientation with four independent constraints [J].ISPRS Journal of Photogrammetry and Remote Sensing,2011,66(6)： 809-817.

[5]赵祖军，柳钦火，刘强,等.利用IMU/GPS信息作为约束进行相对定向[J].应用技术，2006(6)：31-35.

[6]CHANG L,HU B,CHEN S,et al.Comments on Quaternion-Based Method for SINS/SAR Integrated Navigation System [J].Aerospace and Electronic Systems,IEEE Transactions on,2013,49(2)： 1400-1402.

[7]WU S,WU G,TAN S,et al.Quaternion-based adaptive terminal sliding mode control for spacecraft attitude tracking[C].Control and Automation (ICCA),2013 10th IEEE International Conference on,Hangzhou,2013.剑清，潘励，王树根.摄影测量学[M].武汉:武汉大学出版社，2009.

[2]ZHANG Y,HU B,ZHANG J.Relative orientation based on multi-features [J].ISPRS Journal of Photogrammetry and Remote Sensing,2011,66(5)：700-707.

[3]何乔，赵泳，张保明,等.基于广义点的相对定向和绝对定向[J].海洋测绘，2006,26(4)：24-26.

[4]ZHANG Y,HUANG X,HU X,et al.Direct relative orientation with four independent constraints [J].ISPRS Journal of Photogrammetry and Remote Sensing,2011,66(6)： 809-817.

[5]赵祖军，柳钦火，刘强,等.利用IMU/GPS信息作为约束进行相对定向[J].应用技术，2006(6)：31-35.

[6]CHANG L,HU B,CHEN S,et al.Comments on Quaternion-Based Method for SINS/SAR Integrated Navigation System [J].Aerospace and Electronic Systems,IEEE Transactions on,2013,49(2)： 1400-1402.

[7]WU S,WU G,TAN S,et al.Quaternion-based adaptive terminal sliding mode control for spacecraft attitude tracking[C].Control and Automation (ICCA),2013 10th IEEE International Conference on,Hangzhou,2013.

[8]杨化超，卢晓攀，王永波,等.摄影测量共线方程的单位四元数描述[J].中国图像图形学报，2012,17(3)：301-308.

[9]JIANGG,JIANGT,GONGH,etal.ExteriorOrientationofLine-ArrayCCDImagesBasedonQuaternionSphericalLinearInterpolation[C].ISPRSTCVIISymposium-100YearsISPRS,Vienna,2010.

[10]闫利,聂倩,赵展.利用四元数描述线阵CCD影像的空间后方交会[J].武汉大学学报:信息科学版， 2010,35(2)： 201-204.

[11]赵双明,郭秋燕,罗研,等.基于四元数的三维空间相似变换解算[J].武汉大学学报:信息科学版， 2009,34(10)：1214-1217.

[12]周永军，邓才华.利用HGA和单位四元数的相对定向解法[J].武汉大学学报:信息科学版，2011,36(6)：670-673.

[13]DIEBELJ.Representingattitude:Eulerangles,unitquaternions,androtationvectors[J].Matrix,2006.

[14]KUIPERSJB.Quaternionsandrotationsequences[M].Princeton:Princetonuniversitypress,1999.

[15]李德仁，郑肇葆.解析摄影测量学[M].北京:测绘出版社，1992.

[16]周秋生.测量控制网优化设计[M].北京： 测绘出版社，1992.

[17]武汉大学测绘学院测量平差学科组.误差理论与测量平差基础[M].武汉： 武汉大学出版社，2009.

[责任编辑：张德福]