基于北斗三频宽巷组合的RTK 单历元定位方法

基于北斗三频宽巷组合的RTK单历元定位方法

张超1,闻道秋1,潘树国2,高旺1,张小国2

(1.东南大学交通学院，江苏南京210096；2.东南大学仪器科学与工程学院，江苏南京210096)

摘要：为发挥北斗三频超宽巷或宽巷模糊度易于固定的优势，提出一种利用宽巷观测值的北斗单历元定位方法。首先使用载波伪距组合求解最容易固定的(0,-1,1)组合模糊度，其次基于模糊度已固定的(0,-1,1)组合观测值通过CIR方法单历元求解第二个宽巷模糊度(1,-1,0)组合模糊度。(1,-1,0)组合观测值噪声和电离层延迟综合影响最优，因此基于(1,-1,0)组合观测值进行单历元坐标解算。实验结果表明，文中提出的单历元定位方法，能够依据单历元数据最终成功解算出地面点坐标，统计精度为平面2.2 cm，高程5.4 cm，在满足部分领域应用要求的情况下提高效率和抗干扰能力。

关键词：北斗三频；宽巷；单历元定位；RTK；短基线

中图分类号：P228.4

收稿日期：2014-09-25

基金项目：国家科技支撑计划课题(2013BAJ13B01)

作者简介：张超(1989-)，男，硕士研究生.

Single epoch algorithm of short baseline RTK based on triple-frequency wide-lane combination of BDS

ZHANG Chao1,WEN Dao-qiu1,PAN Shu-guo2,GAO Wang1

(1.School of Transportation，Southeast University，Nanjing 210096，China;2.School of Instrument Science and Engineering，Southeast University，Nanjing 210096，China)

Abstract：As for the advantage that triple-frequency extra-wide-lane or wide-line ambiguities are easily fixed，a single epoch algorithm of short baseline RTK based on triple-frequency wide-lane combination is proposed.First the extra-wide-lane ambiguities(0,-1,1) are resolved by carrier-pseudo combination method，then the wide-lane ambiguities(1,-1,0) by CIR(Cascade Integer Resolution) with the fixed ambiguities.The influence of noise and ionosphere delay of the wide-lane ambiguities(0,-1,1) are smallest，so this combination is chozen to resolve the coordinates based on single epoch data.Experimental results show that the single epoch algorithm proposed is feasible to calculate the coordinates，with the statistical positioning error in plane 2 cm，and the error in up direction about 5cm.

Key words：triple frequency of BDS；wide-lane；single epoch algorithm；RTK；short baseline

北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)是我国独立发展、自主运行并与其他卫星导航系统兼容的卫星导航定位系统，并于2012-12-27正式向亚太大部分地区提供连续无源定位、导航、授时等服务[1]。BDS系统卫星全部播发三频信号，是目前唯一的全三频工作的卫星导航系统。多个频点的观测数据具有独特的优势，通过不同频率的线性组合，可以得到一系列波长较长的超宽巷或宽巷组合。结合伪距观测值组合，可以快速解算超宽巷或宽巷组合观测值模糊度[4-6]。模糊度已固定的超宽巷或宽巷观测值即可视为高精度的“伪距”观测量，并应用于高精度快速定位。

实时动态差分技术(Real-Time Kinematic，RTK)，是一种常用的GNSS测量方法。采用实时载波相位差分技术，可以在十秒左右甚至更短的时间内固定模糊度，为用户提供厘米级的定位精度。但是，在强遮挡、可视卫星自身分布均匀性差以及电离层活跃等恶劣观测条件下，RTK需要较长的时间才能固定，甚至不能固定，严重影响RTK的作业效率。另外，传统的RTK算法采用载波、伪距列出的误差方程组一般无法单历元将模糊度固定，因此其定位时间无法达到真正的瞬时。考虑到在一些领域，如水深测量的平面定位、高精度交通导航、道路断面测量等并不要求常规RTK平面1～2 cm、高程优于3～4 cm的定位精度，如果能适当放宽定位精度，来换取定位所需时间的大幅缩短，不仅能够满足工程应用，还可以提高工作效率、适应比较恶劣的观测环境。

1北斗观测值及其线性组合

考虑到双差电离层、对流层残差的影响，北斗双差载波观方程和双差伪距观测方程[3-4]：

(1)

(2)

经过组合的载波和伪距双差观测方程：

(3)

(4)

其中，i,j,k为任意整数；α,β,γ为任意实数；Δφi(i=1,2,3)为第i个频率上的双差载波相位观测值；ΔPi(i=1,2,3)为第i个频率上的双差伪距观测值；λi(i=1,2,3)和ΔNi分别为频率i上的载波波长和双差模糊度；Δρ，ΔT，ΔI分别为双差卫地距、双差对流层延迟值和北斗B1频点上的双差电离层延迟值； f1，f2，f3分别为北斗系统的三个载波频率，频率为f1=1 561.098 MHz，f2=1 207.140 MHz，f3=1 268.520 MHz。

组合的载波观测值与组合的伪距观测值精度：

(5)

其中，μ(i,j,k)，μ(α,β,γ)为组合载波观测值噪声放大因子。对北斗三个频率的观测值进行线性组合，能够构造出一系列具有长波特性的宽巷、超宽巷组合，其模糊度能够得到快速固定[3]。

2三频宽巷组合单历元定位模型

首先，选择一个最容易固定的北斗超宽巷组合，实现单历元模糊度固定；然后，将上一步固定模糊度的超宽巷组合观测值作为精度较高的观测量，与第二个宽巷观测值构成无几何模型，实现第二个宽巷/超宽巷模糊度的单历元固定；最后，采用噪声较小的第二个宽巷观测方程进行单历元定位[7]。

2.1超宽巷/宽巷模糊度固定

1)求解宽巷组合(0,-1,1)模糊度，一般按式(6)进行求解[8]：

(6)

式中：ΔN(0,-1,1)为宽巷组合模糊度，假设载波噪声σΔφ =0.005 m，σΔP =0.6 m，计算的解算中误差为0.092周，固定成功率为100%，表明可以实现单历元固定。但是由于(0,-1,1)组合观测值噪声较大(见表1)[3]，不适合直接用于定位，因此需要解算第二个对应观测值噪声较小的宽巷模糊度。

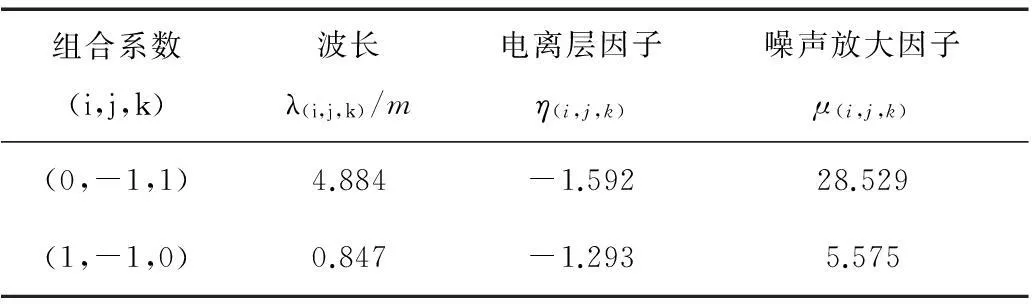
表1　两种北斗宽巷载波组合

2)参照文献[10]，选择第二个噪声放大因子较小的(1，-1，0)观测值组合(见表1)与(0,-1,1)组成无几何模型，根据式(7)求解宽巷组合(1,-1,0)模糊度，并用于其后的单历元定位解算。

(7)

式中：η(i,j,k)，Δεφ(i,j,k)分别为载波组合观测值的电离层延迟因子和组合双差载波观测值噪声。

(8)

根据式(8)分析得知，当电离层延迟为10cm，载波噪声为0.5cm时，模糊度解算成功率为99.81%，因此使用CIR方法求解第二个宽巷模糊度也基本可以实现单历元固定[10]。

2.2基于宽巷组合(1,-1,0)的坐标解算定位解算方程

(9)通过网络RTK区域建模内插得到双差对流层和电离层延迟值，根据卫星高度角对方程进行定权[11-12]，

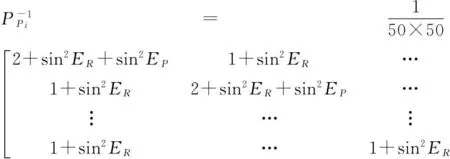
(10)

其中Pφ，Ppi为载波、伪距观测方程权阵，ER，EP分别为参考星和非参考星高度角。式(9)所采用的宽巷组合其观测噪声约为L1的5.58倍，导致定位精度比常规RTK略低，但是，其带来的优势也是明显的，即宽巷模糊度基本可以达到单历元固定，从而实现单历元定位。

3解算实验

本文采用江苏省北斗地基增强系统一期工程中的NJLH和NJLT两个站点组成的基线数据进行实验，基线长度约27.7km，取其中2014-05-06UTC时20:00～21:00的观测数据进行实验解算。该时段可见北斗卫星7颗，以时段内平均高度角最大的C06号卫星为参考卫星。

3.1模糊度解算结果

根据文中所提方法，对宽巷(0,-1,1)进行解算，每颗非参考卫星的解算结果如图1、图2所示。

图1　(0,-1,1)组合超宽巷模糊度单历元解算结果

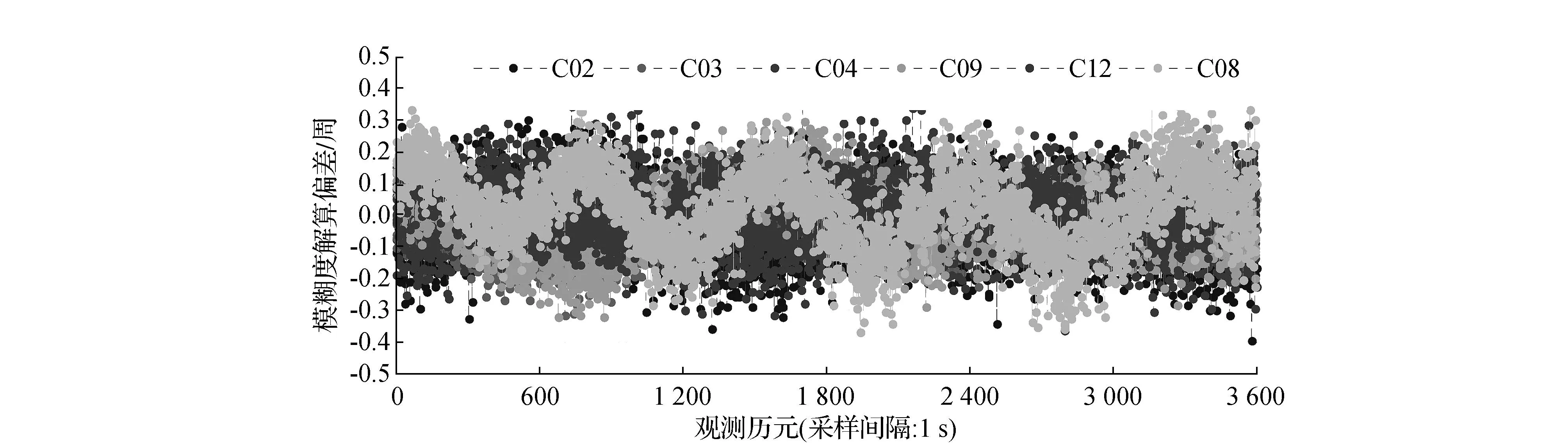
图2　(1,-1,0)组合宽巷模糊度单历元解算结果

从图1看出，依据单历元观测数据解算所得宽巷 (0,-1,1)模糊度，偏差一般在0.1周以内，最多不超过0.2周，因此，单历元固定宽巷模糊度的方法是可行的。然后，利用CIR方法求解第二个宽巷模糊度(1,-1,0)，解算结果如图2所示。

从图2看出，依据CIR方法解算所得宽巷(1,-1,0)模糊度，偏差一般在0.3周以内，最大不超过0.4周，因此，可以实现第二个宽巷模糊度的固定。

3.2定位解算结果

对于3 600个历元分别进行单历元解算，具体解算结果见图3，从图3中可以看出，单历元解算结果，在N和E方向误差基本保持在4cm之内，U方向误差基本保持在10cm之内。对结果进行统计，中误差为σN=0.016 m,σE=0.014 m,σU=0.054 m。由于北斗卫星南北分布均匀性比较差，导致N方向定位精度略低于E方向；而U方向的定位精度显著低于N，E方向，这主要是高程方向几何强度弱于平面方向以及受残余大气误差的影响。

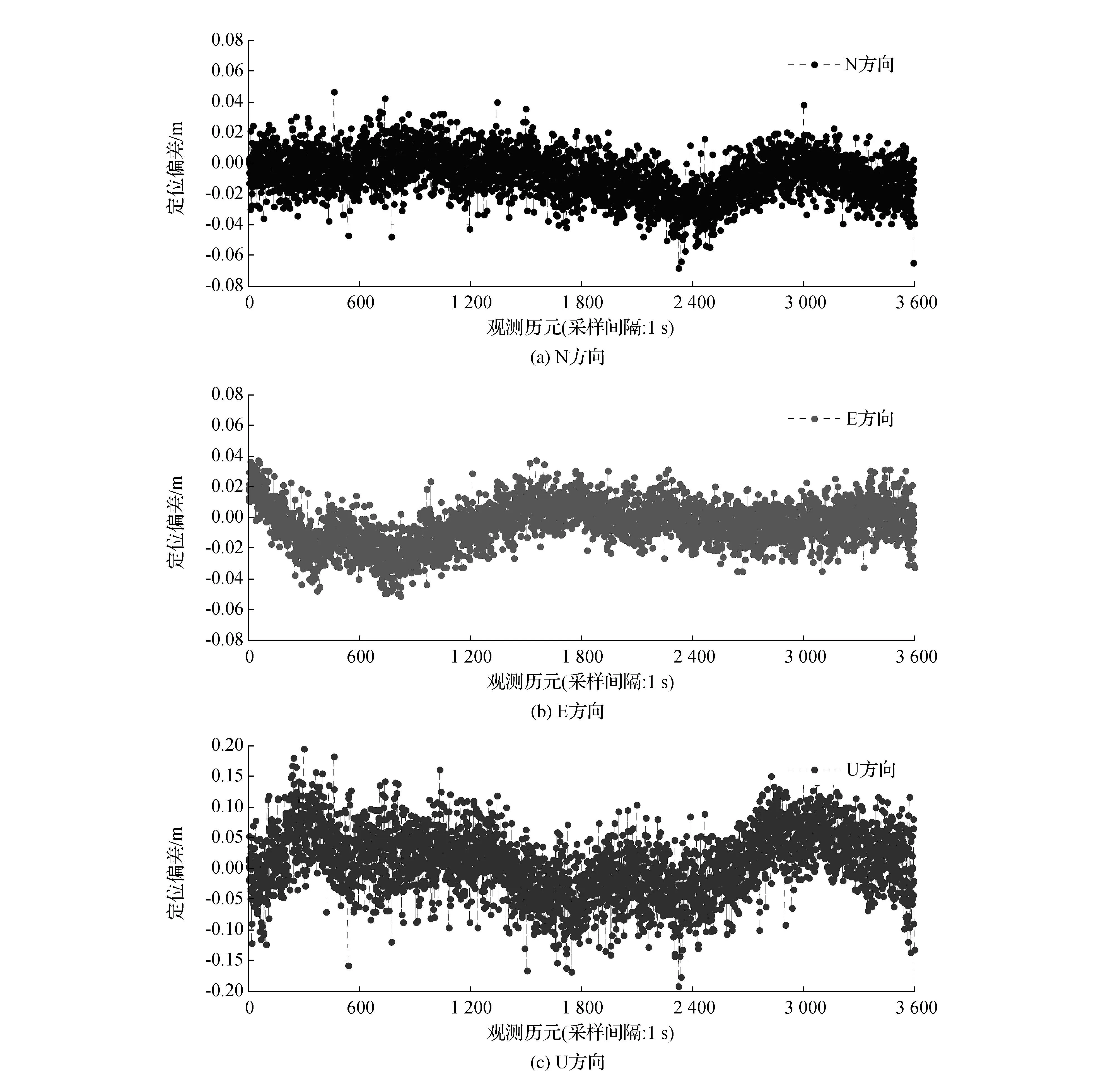
图3　宽巷组合单历元定位偏差(N、E、U方向)

4结论

本文提出的基于宽巷观测值的北斗单历元定位方法，成功的利用了超宽巷组合(0,-1,1)模糊度容易固定的优势实现了超宽巷组合的单历元固定。通过选用观测值噪声和电离层延迟综合影响最优的(1,-1,0)组合，并基于已固定模糊度的组合观测(0,-1,1)值，采用用CIR方法，实现了单历元解算宽巷模糊度组合(1,-1,0)模糊度。最后基于(1,-1,0)组合观测值成功的进行了单历元坐标解算。实验结果表明，提出的单历元定位方法，能够依据单历元数据最终成功解算出地面点坐标，统计精度为平面2.2cm，高程5.4cm。此定位精度略低于传统RTK定位精度，但基于瞬时定位、无初始化时间；且模糊度基于单星解算，对高遮挡等部分观测条件恶劣的环境下有较强的适应能力。在某些对精度要求不是很高，对效率十分敏感的领域，如水深测量的平面定位、高精度交通导航，有较重要的应用价值。

参考文献：

[1]王家伟，范晓伟.中国北斗系统正式服务亚太地区[J].地理教学，2013(4)：4-6.

[2]李博峰，沈云中，周泽波.中长基线三频GNSS模糊度的快速算法[J].测绘学报，2009，38(4)：296-301.

[3]李金龙.GNSS三频精密定位数据处理方法研究[D].郑州:解放军信息工程大学,2011.

[4]RICHERTT，El-SHEIMYN.Optimallinearcombinationsoftriplefrequencycarrierphasedatafromfutureglobalnavigationsatellitesystems[J].GPSSolutions，2007，11(1)：11-19.

[5]CHUFY,YANGM，WUJ.Triple-frequencyGPSambiguityresolutionforpostprocessedmedium-rangebaselinedetermination：aphase-onlymethod[J].JournaloftheChineseInstituteofEngineers，2014，37(3):279-287.

[6]FENGYM，RIZOSC，HIGGINSM.MultiplecarrierambiguityresolutionandperformancebenefitsforRTKandPPPpositioningservicesinregionalareas[C]//ProceedingsofIONGNSS20thinternationaltechnicalmeetingofthesatellitedivision.2007：25-28.

[7]五岳，邱蕾.网络RTK模式下多频载波相位观测值解算整周模糊度[J].测绘工程，2013,22(4):1-4.

[8]WANGK，ROTHACHERM.Ambiguityresolutionfortriple-frequencygeometry-freeandionosphere-freecombinationtestedwithrealdata[J].JournalofGeodesy，2013，87(6)：539-553.

[9]FORSSELLB，MARTIN-NEIRAM，HARRISZRA.CarrierphaseambiguityresolutioninGNSS-2[C]//Proceedingsofthe10thInternationalTechnicalMeetingoftheSatelliteDivisionofTheInstituteofNavigation(IONGPS1997).1997：1727-1736.

[10]王东会,彭竞,王飞雪.北斗信号体制下三频CIR法模糊度解算方法研究[J].全球定位系统，2009(6):13-16.

[11]高成发，赵毅，万德钧.GPS载波定位中双差观测值权的合理确定[J].测绘科学，2005,30(3):28-32.

[12]甘雨，隋立芬，张鹤.利用接收机钟差实时滤波提高GNSS精度[J].测绘工程，2014,23(5):6-8.家伟，范晓伟.中国北斗系统正式服务亚太地区[J].地理教学，2013(4)：4-6.

[2]李博峰，沈云中，周泽波.中长基线三频GNSS模糊度的快速算法[J].测绘学报，2009，38(4)：296-301.

[3]李金龙.GNSS三频精密定位数据处理方法研究[D].郑州:解放军信息工程大学,2011.

[4]RICHERTT，El-SHEIMYN.Optimallinearcombinationsoftriplefrequencycarrierphasedatafromfutureglobalnavigationsatellitesystems[J].GPSSolutions，2007，11(1)：11-19.

[5]CHUFY,YANGM，WUJ.Triple-frequencyGPSambiguityresolutionforpostprocessedmedium-rangebaselinedetermination：aphase-onlymethod[J].JournaloftheChineseInstituteofEngineers，2014，37(3):279-287.

[6]FENGYM，RIZOSC，HIGGINSM.MultiplecarrierambiguityresolutionandperformancebenefitsforRTKandPPPpositioningservicesinregionalareas[C]//ProceedingsofIONGNSS20thinternationaltechnicalmeetingofthesatellitedivision.2007：25-28.

[7]五岳，邱蕾.网络RTK模式下多频载波相位观测值解算整周模糊度[J].测绘工程，2013,22(4):1-4.

[8]WANGK，ROTHACHERM.Ambiguityresolutionfortriple-frequencygeometry-freeandionosphere-freecombinationtestedwithrealdata[J].JournalofGeodesy，2013，87(6)：539-553.

[9]FORSSELLB，MARTIN-NEIRAM，HARRISZRA.CarrierphaseambiguityresolutioninGNSS-2[C]//Proceedingsofthe10thInternationalTechnicalMeetingoftheSatelliteDivisionofTheInstituteofNavigation(IONGPS1997).1997：1727-1736.

[10]王东会,彭竞,王飞雪.北斗信号体制下三频CIR法模糊度解算方法研究[J].全球定位系统，2009(6):13-16.

[11]高成发，赵毅，万德钧.GPS载波定位中双差观测值权的合理确定[J].测绘科学，2005,30(3):28-32.

[12]甘雨，隋立芬，张鹤.利用接收机钟差实时滤波提高GNSS精度[J].测绘工程，2014,23(5):6-8.

[责任编辑：李铭娜]