坐式垂直起降无人机的一种姿态解算算法的设计

刘东辉,奚乐乐,牛孟然,孙晓云，石　楠

(1.河北科技大学电气工程学院， 河北石家庄　050018;2.石家庄铁道大学电气与电子工程学院，河北石家庄　050043)



坐式垂直起降无人机的一种姿态解算算法的设计

刘东辉1,奚乐乐1,牛孟然1,孙晓云2，石楠1

(1.河北科技大学电气工程学院， 河北石家庄050018;2.石家庄铁道大学电气与电子工程学院，河北石家庄050043)

摘要：固定翼模式水平飞行的坐式垂直起降无人机克服了传统固定翼无人机起降条件要求高的缺点，继承了其总体效率高的优点，拥有巨大的发展潜力和非常广阔的应用前景。坐式垂直起降无人机在起降阶段姿态变化范围大，所使用的姿态传感器在俯仰方向的角度变化超过90°时，根据四元数转换出的欧拉角会出现奇异点，即万向节死锁。从解算算法出发，提出了一种更改旋转顺序的方法，避免奇异点出现。结果表明，此方法可以很好地应用在垂直起降无人机的姿态解算上。

关键词：飞行器控制；坐式垂直起降无人机；姿态测量；四元数；欧拉角；万向节死锁

E-mail：liudh@hebust.edu.cn

刘东辉,奚乐乐,牛孟然，等.坐式垂直起降无人机的一种姿态解算算法的设计[J].河北科技大学学报,2016,37(1):47-51.

LIU Donghui, XI Lele, NIU Mengran,et al.Design of attitude solution algorithm for tail-sitter VTOL UAV[J].Journal of Hebei University of Science and Technology,2016,37(1):47-51.

目前，传统固定翼布局无人机的总体效率很高，但其起飞和降落过程对环境要求特别高，限制了其实际应用[1-2]。坐式垂直起降飞机是一种以垂直姿态，“坐”于地面的垂直起降飞行器，由于无人机不必考虑载员的姿势，故而无人机非常适于采用此种垂直起降方式。它既保持高效率的传统固定翼飞机构型，具有固定翼无人机飞行速度快、航程远、反应灵活等特点，又具有直升机的垂直起降功能，降低起飞降落过程对环境的要求。随着科技的发展，坐式垂直起降无人机受到了人们广泛的关注，在军事、民用等多方面都有非常广阔的发展前景[3]。例如，垂直起降无人机可应用在高速巡航、应急运输、冰面爆破、侦察、航拍航测等多种领域。

姿态测量系统及其算法是垂直起降无人机控制系统的核心部分。本文中坐式垂直起降无人机的姿态测量系统采用廉价且稳定性高的MPU-6050作为姿态传感器，该传感器具有6个自由度，整合了三轴加速度计和三轴陀螺仪。同时，MPU-6050内部集成了可控式的运动处理器DMP，并可通过IIC协议与第三方传感器相连接，比如气压传感器。结合高效的微处理器，大大增加系统的稳定性和精确性，同时保持了极低的硬件成本[4-6]。

但是，坐式垂直起降无人机在垂直-水平姿态转换过程中，俯仰方向会发生达到甚至超过90°的变化，MPU-6050的其他2个轴的角度解算值会发生突变，使得坐式垂直起降无人机失去惯性基准，很容易导致飞机失控坠毁。针对这个关键问题，本文提出一种合理的姿态角测量解算方式，提供稳定、准确的惯性基准[7-8]。

1姿态解算问题

万向节死锁(Gimbal Lock)一般又被称为万向节锁或者万向锁，是指当3个万向节中的2个轴发生重合时，会失去一个自由度的现象。在飞行器姿态运动学方程中一般有四元数和欧拉角2种表示方式，也是最常用的2种姿态表示方法。用欧拉角表示的飞行器姿态运动学方程在大角度时会出现奇异点并进入所谓的“万向节死锁”状态。而采用四元数来表示，则可以避免这个问题。因此，飞行器运动学方程常采用四元数来表示[9-11]。但是欧拉角表示姿态角比起四元数更加形象、直观，具有明确的几何意义，更易于被人理解。本文采用四元数的方法进行姿态解算，然后将四元数转换为欧拉角。在转换过程中，转换结果和旋转顺序存在必然顺序关系。在表示某一个姿态的过程中，四元数是唯一的，但是不同的旋转顺序会得到不同的欧拉角。所以针对不同的旋转顺序，四元数和欧拉角之间存在一对多的情况[12-13]。本系统采用的坐式垂直起降无人机和传感器安装示意图如图1中的图1 a)和图1 b)所示。

图1　坐式垂直起降无人机和传感器安装示意图Fig.1　VTOL UAV and sensor installation schematic diagram

在传统的姿态解算过程中，一般的四元数转欧拉角[14-15]过程采用Z-Y-X的旋转顺序，设定四元数：

Q=w+xi+yj+zk，

且绕X轴旋转的角度为φ，绕Y轴旋转的角度为θ，绕Z轴旋转的角度为ψ。四元数转欧拉角的转换公式如式(1)所示。

(1)

按照Z-Y-X旋转顺序进行旋转的示意图如图2中的图2 a)和图2 b)所示。这种情况下，外圆环代表航向(ψ)，中圆环代表俯仰(θ)，内圆环代表横滚(φ)。Z轴为Y轴的父级，Y轴为X轴的父级，X轴为箭头的父级，当绕着Y轴旋转90°或-90°时，Z轴和X轴将会出现上述的重合情况，便会发生万向节死锁。图2中的图2 a)为先绕Z轴旋转45°的结果，图2 b)为绕Y轴旋转90°后的结果。可以很明显地看出，外圆环和内圆环转到了一个平面上，这个时候当再次旋转内圆环或外圆环时，外圆环与内圆环仍然在一个平面上，所以得到的结果是一样的，这便是万向节死锁。

根据万向节死锁的特性，一般绕着中间轴旋转90°时会出现奇异现象，所以可以根据系统的要求，改变四元数转换为欧拉角时的旋转顺序，从而避免垂直起降飞机在俯仰变化范围超过90°过程中出现奇异点。所以，在坐式垂直起降无人机上的姿态解算不能采用传统的Z-Y-X旋转顺序。针对这种情况，可以采用变换旋转顺序的方法克服Y轴在90°时候的奇异点，以达到坐式垂直起降无人机姿态解算的正确性。例如采用Z-X-Y顺序进行四元数到欧拉角的转换。

图3中的图3a)和图3b)为按照Z-X-Y旋转顺序进行旋转的结果，Z为X的父级，X为Y的父级，Y为箭头的父级。其中图3a)为沿着Y轴旋转90°的结果，图3b)为沿着X轴旋转60°结果。因坐式垂直起降无人机正常情况下，沿X轴(横滚)方向几乎不会出现90°的旋转，这样便克服了万向节死锁现象的发生。按照Z-X-Y旋转顺序进行旋转时的四元数转欧拉角公式如式(2)所示：

(2)

图2　按Z-Y-X顺序旋转示意图Fig.2　Rotation diagram in Z-Y-X order

图3　按Z-X-Y顺序旋转示意图Fig.3　Rotation diagram in Z-X-Y order

2实验研究

本测试系统通过读取MPU-6050传感器的原始数据[16-17]，得到三轴陀螺仪数据和三轴加速度数据，并通过互补滤波算法进行数据的融合，得到四元数，然后根据旋转顺序来选择四元数转欧拉角公式，得到最终的欧拉角。在比较过程中，本系统采用STM32系列微处理器[18]进行数据融合，并将更新的四元数通过Z-Y-X和Z-X-Y2种转换公式进行四元数到欧拉角的转换，并通过串口将2种旋转顺序输出的角度φ，θ，ψ同时打印出来，通过Matlab软件进行数据处理，得到数据融合的曲线。按Z-Y-X顺序和按Z-X-Y顺序旋转生成的欧拉角数据图如图4和图5所示。

在图4中，横轴为时间轴，纵轴为各姿态轴的角度。数据采集过程的初期，飞机处于水平飞行姿态，飞机俯仰角(θ)保持基本稳定，滚转角(φ)和方向角(ψ)能够在一定范围内被测量。但当俯仰角达到90°时，滚转角和方向角都出现了剧烈的变化，并出现异常值；随着俯仰角在90°左右变化，滚转角和方向角反复在±180°范围内剧烈震荡，完全失去参考价值。

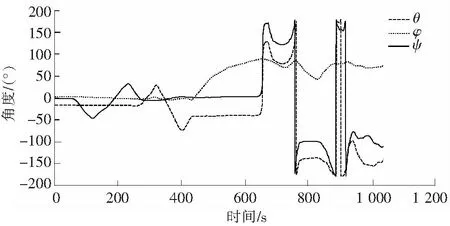
图4　按Z-Y-X顺序旋转数据图Fig.4　Rotation data graph in Z-Y-X order

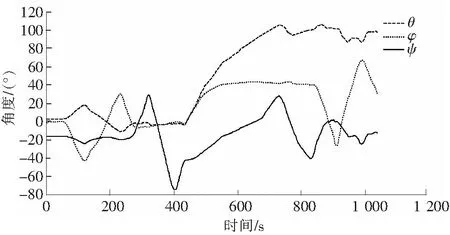
图5　按Z-X-Y顺序旋转数据图Fig.5　Rotation data graph in Z-X-Y order

在图5中，横轴为时间轴，纵轴为各姿态轴的角度。数据采集过程的初期，飞机处于水平飞行姿态，飞机俯仰角(φ)保持基本稳定，滚转角(θ)和方向角(ψ)能够在一定范围内被测量。当飞机俯仰角逐渐变大并达到90°时，滚转角和方向角都能在一定范围内被测量，并没有剧烈震荡的奇异点出现，在垂直起降无人机的姿态解算系统中可以被采用。

3结语

通过调整四元数转换欧拉角的旋转顺序，可以非常有效地解决出现奇异点的情况，避免万向节死锁现象的发生。实验证明，在四元数转欧拉角的过程中，选择Z-Y-X旋转顺序在俯仰方向旋转出现90°或者-90°时，便会发生奇异现象，其他2个轴的输出角度会发生突变，无法得到正确的姿态信息[19-20]。而在相同情况下，Z-X-Y旋转顺序下输出的角度不会出现奇异现象，所以选择合理的旋转顺序，可以有效避免坐式垂直起降无人机在俯仰方向变化90°时给偏转和横滚方向造成的角度突变的发生，解决了坐式垂直起降无人机姿态解算的一个问题。

参考文献/References:

[1]秦博,王蕾.无人机发展综述[J].飞航导弹,2002(8):4-10.

QIN Bo, WANG Lei. The review about the UAV[J].Aerodynamic Missile Journal,2002(8):4-10.

[2]王冠林，武哲.垂直起降无人机总体方案分析及控制策略综合研究[J].飞机设计,2006(3):25-30.

WANG Guanlin,WU Zhe.Configurations and control strategy for VTOL[J].Aircraft Design,2006(3):25-30.

[3]赖水清,严峰,徐珂.倾转旋翼机过渡飞行阶段控制律设计研究[J]. 直升机技术, 2009(3):52-55.

LAI Shuiqing, YAN Feng, XU Ke. Design and research of control law for tilt rotor in transition flight phase[J]. Helicopter Technique,2009(3):52-55.

[4]冯智勇,曾瀚,张力,等.基于陀螺仪及加速度计信号融合的姿态角度测量[J]. 西南师范大学学报(自然科学版), 2011,36(4):137-141.

FENG Zhiyong, ZENG Han, ZHANG Li, et al. Angle measurement based on gyroscope and accelerometer signal fusion[J]. Journal of Southwest China Normal University(Natural Science Edition),2011,36(4):137-141.

[5]刘东辉,刘浩,孙晓云,等.装甲车辆模拟射击中身管角度采集装置设计[J].河北科技大学学报,2014,35(4):376-383.

LIU Donghui, LIU Hao, SUN Xiaoyun, et al. Design of barrel angle acquisition device in the simulated shooting of armored vehicles[J]. Journal of Hebei University of Science and Technology,2014,35(4):376-383.

[6]王书岩. 利用STM32片内A/D实现的同步电机数据采集控制器[J].河北工业科技，2014,31(2):177-180.

WANG Shuyan. Realization of synchronous motor data acquisition controller based on multi-channel A/D of STM32 chip[J]. Hebei Journal of Industrial Science and Technology, 2014,31(2):177-180.

[7]张帆,曹喜滨,邹经湘.一种新的全角度四元数与欧拉角的转换算法[J].南京理工大学学报(自然科学版),2002,26(4):376-380.

ZHANG Fan, CAO Xibin, ZOU Jingxiang. A New large-scale transformation algorithm of quaternion to euler angle[J]. Journal of Nanjing University of Science and Technology,2002,26(4):376-380.

[8]王海峰,王成良.解决欧拉方程奇异性的方法探讨[J]. 飞行力学, 2006,24(3):94-96.

WANG Haifeng,WANG Chengliang. A new solution for singularity of euler equations[J]. Flight Dynamics,2006,24(3):94-96.

[9]熊志斌,刘喜斌.克服欧拉方程奇异性的方法研究[J]. 岳阳师范学院学报(自然科学版), 2000,13(4):60-62.

XIONG Zhibin,LIU Xibin. Research on methods for overcome the singularity of the Euler equation[J]. Journal of Yueyang Normal University,2000,13(4):60-62.

[10]许毛跃,张登成,李嘉林.四元数在欧拉方程中的应用研究[J].飞行力学,2002,20(1):67-70.

XU Maoyue, ZHANG Dengcheng, LI Jialin. Study of the application of quaternion to euler equation[J].Flight Dynamics,2002,20(1):67-70.

[11]郭访社,于云峰,刘书盼,等.捷联惯导系统姿态更新旋转矢量算法的优化[J]. 计算机工程与科学, 2008,30(9):69-72.

GUO Fangshe,YU Yunfeng,LIU Shupan, et al.Optimization of the rotation vector algorithm for strap down inertial navigation system attitude updating[J]. Computer Engineering & Science,2008,30(9):69-72.

[12]余杨,张洪钺.高精度捷联姿态算法设计[J].中国惯性技术学报,2008,16(1):39-43.

YU Yang, ZHANG Hongyue. Design for an accurate strap down attitude algorithm[J].Journal of Chinese Inertial Technology,2008,16(1):39-43.

[13]刘俊峰.三维转动的四元数表述[J].大学物理,2004,23(4):39-43.

LIU Junfeng. The quaternion describe for three-dimensional [J].College Physics,2004,23(4):39-43.

[14]梁延德,程敏,何福本,等.基于互补滤波器的四旋翼飞行器姿态解算[J].传感器与微系统,2011,30(11):56-61.

LIANG Yande, CHENG Min, HE Fuben, et al. Attitude estimation of a quad- rotor aircraft based on complementary filter[J]. Transducer and Microsystem Technologies,2011,30(11):56-61.

[15]乔相伟,周卫东,吉宇人.基于四元数粒子滤波的飞行器姿态估计算法研究[J].兵工学报,2012,33(9):1070-1074.

QIAO Xiangwei, ZHOU Weidong, JI Yuren. Study on aerial vehicle attitude estimation based on quaternion particle filter algorithm[J]. Acta Armamentarii,2012,33(9):1070-1074.

[16]刘东辉,赵新伟,李天宝,等. 无位置传感器无刷直流电机数控调速器设计[J].河北科技大学学报,2013,34(4):302-307.

LIU Donghui, ZHAO Xinwei,LI Tianbao, et al. Design of digital controller for sensorless brushless DC motor speed regulation[J].Journal of Hebei University of Science and Technology,2013,34(4):302-307.

[17]刘忠,梁晓庚,曹秉刚,等. 基于四元数的空间全方位算法研究 [J].西安交通大学学报,2006,40(5):618-620.

LIU Zhong, LIANG Xiaogeng, CAO Binggang, et al. Space omni directional algorithm study based on quaterion[J]. Journal of Xi'an Jiaotong University, 2006,40(5):618-620.

[18]王书岩.利用Cortex-M3实现同步电动机失步保护的装置[J].河北工业科技,2012,29(6):426-428.

WANG Shuyan. Using Cortex-M3 to realize synchronous motor out-of-step protection device[J]. Hebei Journal of Industrial Science and Technology, 2012,29(6):426-428.

[19]李连仲,王小虎,蔡述江.捷联惯性导航、制导系统中方向余弦矩阵的递推算法 [J].宇航学报,2006,27(3):349-353.

LI Lianzhong, WANG Xiaohu, CAI Shujiang. A new recursion figure used in the matrix of the direction cosine in the strap down intertial navigation and guideance system[J].Journal of Astronautics,2006,27(3):349-353.

[20]陈万春,肖业伦.矢阵与四元数的关系及其在飞行力学中的应用[J].宇航学报,1997,18(1):23-30.

CHEN Wanchun, XIAO Yelun. Vectrixized quaterion and its application in flight dynamics[J].Journal of Astronautics, 1997,18(1):23-30.

Design of attitude solution algorithm for tail-sitter VTOL UAV

LIU Donghui1, XI Lele1, NIU Mengran1, SUN Xiaoyun2， SHI Nan1

(1.School of Electrical Engineering, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China; 2.School of Electrical and Electronic Engineering, Shijiazhuang Tiedao University, Shijiazhuang, Hebei 050043, China)

Abstract:The tail-sitter Vertical Takeoff and Landing (VTOL) Unmanned Aerial Vehicle(UAV), flying in a fixed-wing model, overcomes many shortcomings of traditional fixed-wing UAVs, and inherits the advantage of high overall efficiency, which means it has great development potential and very broad application prospects. The attitude of tail-sitter VTOL UAV shows a wide change range in its takeoff and landing stages, and when the attitude sensor changes more than 90 degrees in pitch direction, the Euler angles converted by the Quaternions will have singular points, which means gimbal deadlock appears. From the solution algorithm, this paper provides a method of changing the order of rotation to avoid the appearance of singular points. The results show that this method can be well applied to the attitude solution of the VTOL UAV.

Keywords:aircraft control; tail-sitter VTOL UAV; attitude measuring; quaternion; Euler angle; gimbal deadlock

作者简介：刘东辉(1971—)，男，山西晋城人，教授，博士，主要从事电器信息检测与信息处理技术方面的研究。

基金项目：国家自然科学基金(51274144)

收稿日期：2015-07-16；修回日期：2015-11-03；责任编辑：李穆

中图分类号：V249.1

文献标志码：A

doi:10.7535/hbkd.2016yx01008

文章编号：1008-1542(2016)01-0047-05