利用 GRACE 卫星 Level-1B 数据反演陆地水储量变化的方法研究

2015-12-29郭飞霄,肖云,汪菲菲等

测绘工程 2015年6期

利用GRACE卫星Level-1B数据反演陆地水储量变化的方法研究

郭飞霄1,2，肖云1,2，汪菲菲3，苗岳旺3

(1.西安测绘研究所，陕西西安710054;2.地理信息工程国家重点实验室，陕西西安710054;3.西安测绘信息技术总站，陕西西安710054)

摘要：卫星重力探测技术为监测陆地水储量变化提供了新的技术手段。对利用GRACE卫星Level-1B数据反演地球陆地水储量变化的重力位差法和Mascon方法的数学模型作了详细推导分析，总结两种方法的特点和解算处理步骤。推导过程表明：重力位差法和Mascon方法在反演时只采用卫星飞临研究区域上空时的观测数据，能够提高反演结果的空间分辨率，比传统的球谐系数法更具优势；Mascon方法在解算时还引入了时空约束方程，进一步提高了反演结果的时空分辨率。

关键词：卫星重力探测；陆地水储量；GRACE卫星；Mascon方法；重力位差

中图分类号：TP72;P228

收稿日期：2014-05-21

基金项目：国家自然科学基金资助项目(41374083)；国家重点基础研究发展计划 (2013CB733303-2)；大地测量与地球动力学国家重点实验室开放基金资助项目(SKLGED2013-3-3-E)

作者简介：郭飞霄(1988-)，男，硕士.

A study of the methods of recovering continental water storage variation using GRACE Level-1B data

GUO Fei-xiao1,2,XIAO Yun1,2,WANG Fei-fei3,MIAO Yue-wang3

(1.Xi’an Research Institute of Surveying and Mapping,Xi’an 710054,China;2.State Key Laboratory of Geo-Information Engineering,Xi’an 710054,China;3.Technical Division of Surveying and Mapping,Xi’an 710054,China.)

Abstract：Technology of satellite gravimetry provides a new technical means for monitoring continental water storage variation.Mathematical models of Mascon and situ geopotential using GRACE Level-1B data for recovering continental water storage variation are deduced detailedly.The characteristic and processing steps of the two methods are summarized.It is showed that methods of Mascon and situ geopotential can promote the spatial resolution of result and have more advantages than the method of spheric harmonic coefficient because of using range rate observations only when satellites flying over study area.Constraint equation is introduced into Mascon method processing,and further promotes the spatial and temporal resolution.

Key words：satellite gravimetry；continental water storage；GRACE satellite；mascon method；situ geopotential

地球重力场及其时变效应反映了地球表层及内部物质的重新分布和质量迁移变化。当前，全球性环境问题如海平面上升、极地冰川融化等与地球表层的物质迁移紧密相关。因此，研究地球系统的质量迁移和重新分布对监测全球环境和气候变化具有重要的意义[1]。水资源变化是每个国家经济和社会发展最关心的问题之一，陆地水储量变化的准确估计对气候变化的研究和预报、农业生产和防灾减灾等方面具有重要的现实意义。我国是水资源匮乏国家，近年来随着人口的持续增长和经济的高速发展，水资源匮乏问题逐步凸显。因此，监测陆地水储量变化趋势将有着巨大的经济效益和社会意义。但是，地基台站观测覆盖范围小且空间分布不均匀，传统的卫星遥感技术也只能观测到地表十几厘米厚度的土壤湿度变化[2]。2002年3月，GRACE卫星的成功发射开创了高时空分辨率监测全球重力场的新纪元，也为监测陆地水储量变化提供了新的技术手段。卫星重力探测技术作为遥感的一种新技术[3]，适用于中长空间尺度陆地水储量变化的监测，且观测尺度统一、全球分布均匀，在中长空间尺度上可有效弥补遥感卫星只能观测地表土壤湿度以及地基观测台站空间分布不均匀等不足，目前已广泛应用于全球及区域陆地水储量变化研究[4-7]。

当前，利用GRACE卫星数据反演陆地水储量变化大多采用球谐系数法[8]，该方法采用GRACE卫星Level-2数据的时变重力场模型，反演结果的时间分辨率为30 d，空间分辨率约为800 km。为进一步提高陆地水储量变化反演结果的时空分辨率，国外学者利用星间距离变率观测值对地球表层质量变化异常敏感的特性，用Level-1B级数据的KBRR(K-Band Range Rate)、GPS和加速度计观测值直接推求陆地水储量变化。根据反演原理的不同有两种方法：重力位差法[9-11]和Mascon(Mass concentration)方法[12-14]。研究结果表明：利用Level-1B数据可以有效提高反演结果的时空分辨率，反演结果时间分辨率甚至可达10 d左右，空间分辨率可提高到200 km左右[11-12]，比球谐系数法更具优势。国内针对利用Level-1B数据反演陆地水储量变化的研究起步较晚。本文针对利用Level-1B数据反演陆地水储量变化的方法进行了研究，详细推导分析了重力位差法和Mascon方法的数学模型。

1重力位差法

两颗卫星间的瞬时重力位差是恢复地球重力场的重要观测量，可以建立起与地球重力场的直接显式关系式，获得较高精度的地球重力场模型。并且，利用重力位差观测量还可以高频率直接感知获取区域重力场信号随时间的变化，进而反演地球表层区域的质量变化[15]。

1.1基本原理

根据能量守恒原理，推导两颗卫星的瞬时重力位差观测方程如下[16]:

(1)

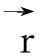
(2)

地球表层的质量迁移变化都会引起两颗卫星重力位差的变化，两颗卫星的重力位差可表示为如下形式:

(3)

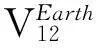
行星引力、潮汐、大气和海洋等效应当前已有较好的模型去去除，因此在去除这些效应引起的重力位差后，由式(3)可以得到

(4)

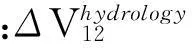
1.2观测方程

地球表层区域的物质质量迁移变化会引起地球重力场的局部变化，对于陆地区域，地球质量变化主要是陆地水储量的变化。因此，根据牛顿万有引力定律，采用点质量模型，如图1所示将研究区域划分成一定大小的网格，t时刻某区域陆地水储量变化引起的两颗卫星重力位差[17]

(5)

其中:

(6)

式中:lj为网格j中心点到卫星的距离;网格(r1,θ1,λ1)为前星的地心向径、余纬和经度;(r2,θ2,λ2)为后星的地心向径、余纬和经度;Δm(θj,λj,t)为第j个网格区域t时刻的水储量变化;(θj,λj)为第j个区域网格中心点的余纬和经度;R为地球半径;G为万有引力常数;n为网格总数。

进一步，Δm(θj,λj,t)可表示为

(7)

式中:ρw为水的密度，(RΔθ)(RΔλsinθj)为网格区域j的水平面积，Δhj(t)为网格j内质量变化的等效水柱高度。将式(7)代入式(5)可得

(8)

式(4)和式(8)表明，可以通过星载GPS观测值、KBRR观测值和加速度计数据求得两颗卫星的重力位差，进而反演陆地水储量变化。

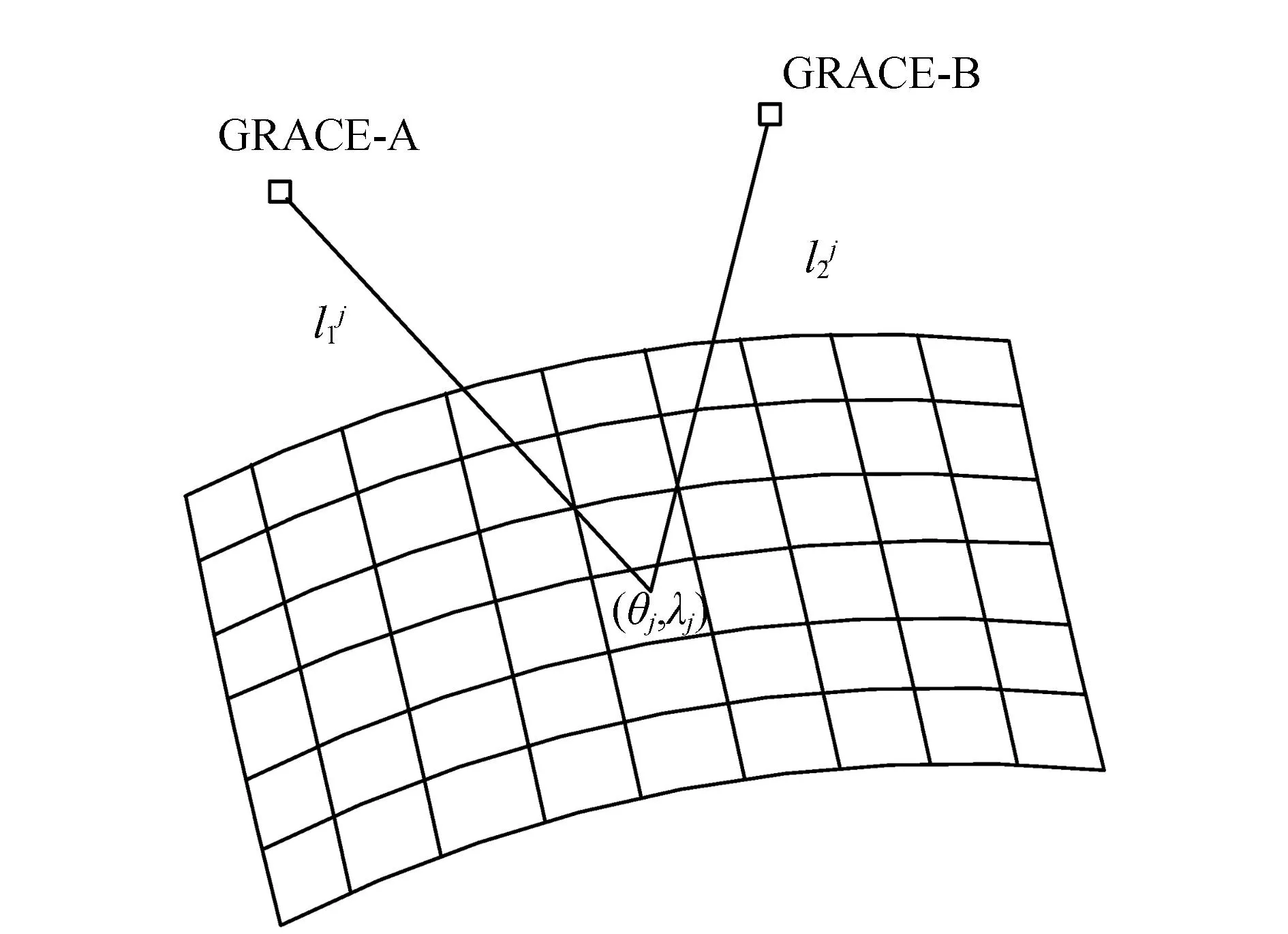
图1　重力位差法反演陆地水储量变化原理

1.3参数估计

将式(8)可写成误差方程组形式为

(9)

采用卫星测量数据确定地球表面物理量向下延拓的过程是个病态问题。因此，采用最小二乘平差解算上述误差方程组，解算时法方程组是病态的。引入参数的先验信息有助于解决该病态问题[9]。设待估参数向量x的先验期望值为x0，Cx为先验协方差阵，于是可得

(10)

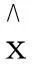
(11)

2Mascon方法

Mascon方法最初被应用于研究月球表面质量异常导致的引力扰动[18]，Rowland将该方法应用于GRACE卫星KBRR观测数据恢复区域时变重力场的研究[12]。目前，Mascon方法已在多个领域取得了丰富的研究成果，是当前GRACE时变重力场研究的热点。

2.1基本原理

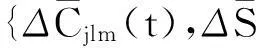
(12)

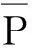
σj(t)可写成σj(t)=10×Hj(t)。比例因子10 的含义是1 m2区域内质量增加或减少10 kg等效为区域内水柱升高或减少1 cm，Hj(t)为t时刻网格j内质量变化的等效水柱高度，单位为cm，Hj(t)即Mascon参数。由于重力卫星对地球表层区域质量变化的时间分辨率是有限的，故认为在一定时间段内同一网格区域j的Mascon参数Hj(t)是不变的。因此式(12)又可改写为如下形式：

(13)

(14)

对研究区域内所有网格采取以上相同处理，可得到式(15)，式中N1为Mascon参数个数。

(15)

2.2观测方程

根据基于星间距离变率数据确定地球重力场模型的数学推导[19]，可建立星间距离变率观测值与Mascon参数间的关系式如下：

(16)

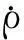
(17)

研究结果表明，地球表层区域的质量变化对GRACE卫星KBRR观测数据的影响在空间范围是有限的[20]，因此Mascon方法在反演陆地水储量变化时仅采用卫星飞临研究区域上空时的KBRR观测数据。式(16)将Mascon参数与KBRR观测值联系起来，是Mascon反演陆地水储量变化的观测方程。

2.3时间-空间约束方程

在空间上邻近的网格区域，受相近的环境影响，水储量变化应该在数值上是连续的，而不应存在跳跃变化。并且对同一个网格区域，在邻近时间段内该网格区域内的质量变化数值上也是趋于一致的。因此，可引入时间-空间约束方程如下[13]：

(18)

对任意两个Mascon参数Hn和Hk，其中n≠k，满足上述约束方程，可以认为两者在数值上趋于一致的“可能性”满足一个与它们之间的空间和时间“距离”相关的指数函数[14]。

(19)

式中:tnk是两个Mascon参数在时间上的“距离”，dnk是两Mascon参数所在网格的空间距离。T和D是表征了Mascon参数解的约束程度，与研究区域的网格划分有关。从式(19)可以看出，两个Mascon参数在时空上的“距离”越小，它们在数值上接近的可能性越大；反之，二者差异越大。

2.4参数估计

将时间-空间约束方程(18)看作虚拟观测方程。在对Mascon参数进行平差解算时，存在两类观测方程：KBRR观测方程和虚拟观测方程。因此，需要对虚拟观测方程赋予合适的权因子Pnk，分析知，可设置为[21]

(20)

式中，S为虚拟观测方程相对于KBRR观测方程取单位权时的比例因子，取值一般是经验性的，也可以采用赫尔默特方差分量估计。

联立式(16)和式(18)，写成误差方程组的形式

(21)

其中:δX为待估参数，包括Mascon参数H和基线参数y0，A和B分别为观测方程(16)和(18)线性化后的系数矩阵，L为观测值。设P1和P2分别是KBRR观测方程组和虚拟观测方程组的权阵，对式(21)进行平差解算可得

[ATP1A+BTP2B]-1[ATP1L1+BTP2L2]=δX.

(22)

解该线性方程组，即可求得Mascon参数解。

3结束语

由重力位差法和Mascon方法的推导过程可知，两种方法在利用GRACE卫星Level-1B数据反演陆地水储量变化时都只采用了卫星飞临研究区域上空时的观测数据，理论上能够提高反演结果的空间分辨率。并且，Mascon方法在解算时还引入了时空约束方程，能够进一步提高反演结果的时间分辨率，并使得解算结果更加符合实际。与球谐系数法相比，利用GRACE卫星Level-1B数据的反演结果时间和空间分辨率更高，具有更大的优势。

参考文献：

[1]朱广彬.利用GRACE位模型研究陆地水储量的时变特征[D].北京：中国测绘科学研究院，2007.

[2]国家测绘地理信息局,遥感卫星[EB/OL]，http://sasmac.sbsm.gov.cn/article/kpzs/200912/20091200059269.shtml.

[3]钟敏，段建宾，许厚泽，等.利用卫星重力观测研究近5年中国陆地水量中长空间尺度的变化趋势[J].科学通报，2009，54(9)：1290-1294.

[4]罗志才，李琼，钟波.利用GRACE时变重力场反演黑河流域水储量变化[J].测绘学报，2012,41(5):676-682.

[5]李琼，罗志才，钟波．利用GRACE时变重力场探测2010年中国西南干旱陆地水储量变化[J].地球物理学报，2012，41(5):676-673.

[6]刑乐林，李辉，刘冬至,等.利用GRACE时变重力场监测中国及其周边地区水储量月变化[J].大地测量与地球动力学，2007,27(4)：35-39.

[7]程朋根，郑守住，陈晓勇，等.GNSS-R技术在海冰反演中的应用[J].测绘工程，2014,23(4)：1-3.

[8]WAHRJ,MOLEVARARM,BRYANF.TimevariabilityoftheEarth’sgravityfield：hydrologicalandoceaniceffectsandtheirpossibledetectionusingGRACE[J].J.Geophys.Res,1998，103,30205-30229.

[9]HANSC,SHUMCK,BRAUNK.High-resolutioncontinentalwaterstoragerecoveryfromlow-lowsatellite-to-satellitetracking[J].JournalofGeodynamics,2005,39:11-28.

[10]HANSC,SHUMCK,JEKELIC,etal.ImprovedestimationofterrestrialwaterstoragechangesfromGRACE[J].GeophysicalResearchLetters,2005,Vol.32,L07302.

[11]王雷.GRACE时变重力场[D].武汉:武汉大学，2006.

[12]ROWLANDSDD,LUTHCKESB,KLOSKOSM,etal.ResolvingmassfluxathighspatialandtemporalresolutionusingGRACEintersatellitemeasurements[J].GeophysicalResearchLetters，2005,Vol.32,L04310.

[13]ROWLANDSDD,LUTHCKESB,MCCARTHYJJ,etal.GlobalmassfluxsolutionsfromGRACE：Acomparisonofparameterestimationstrategies-MassconcentrationsversusStokescoefficients[J].JournalofGeophysicalResearch,2010,Vol.115,B01403.

[14]张坤.基于Mascon方法确定时变地球重力场的研究[D].武汉:武汉大学，2011.

[15]王正涛，姜卫平，晁定波.卫星跟踪卫星测量确定地球重力场的理论和方法[M].武汉:武汉大学出版社，2011.

[16]JEKELIC.Thedeterminationofgravitationalpotentialdifferencesfromsatellite-to-satellitetracking[J].Celest.Mech.Dyn.Astron,1999,75:85-100.

[17]PAILR.Syntheticglobalgravitymodelforplanetarybodiesandapplicationsinsatellitegravitygradiometry[D].Ph.D.dissertation,TechnicalUniversityGraz,1999.

[18]邢乐林，李建成，沈飞,等.点质模型求定月球重力场及其特征分析[J].测绘科学，2008,33(1)：36-40.

[19]肖云.基于卫星跟踪卫星数据恢复地球重力场的研究[D].郑州：信息工程大学，2006.

[20]LEMOINEFG,LUTHCKESB,ROWLANDSDD,etal.Theuseofmasconstoresolvetime-variablegravityfromGRACE[J].InternationalAssociationofGeodesySymposia,2007,130:231-236.

[21]KLOSKOS,ROWLANDSDD,LUTHCKESB,etal.EvaluationandvalidationofmasconrecoveryusingGRACEKBRRdatawithindependentmassfluxestimateintheMississippiBasin[J].JGeod,2009,83:817-827.广彬.利用GRACE位模型研究陆地水储量的时变特征[D].北京：中国测绘科学研究院，2007.