改进的GM（1，1）模型在大坝变形预测中的应用

改进的GM(1,1) 模型在大坝变形预测中的应用

任远军1，李龙2，石宁3，罗勇3

(1.湖北清江水电开发有限责任公司，湖北宜昌443000；2.中铁港航局集团航道工程有限公司，广东广州510660；3.中南大学地球科学与信息物理学院，湖南长沙410083)

摘要：针对大坝安全监测数据存在贫信息、小样本的问题，通过对原始数据、初始值以及背景值进行优化改进传统的 GM(1,1) 模型。以某大坝实测径向水平位移数据为例，分别用改进前后的模型进行预测，并与实测值进行对比。验证改进的 GM(1,1) 模型的优越性与有效性，相对于传统 GM(1,1) 模型，其预测精度更高。

关键词：大坝监测；GM(1,1) 模型；改进 GM(1,1) 模型；预测

中图分类号：TU196

收稿日期：2014-04-17;修回日期：2014-08-20

作者简介：任远军(1987-)，男,助工.

ApplicationofimprovedGM(1,1)modeltodamdeformationforecastingRENYuan-jun1，LI Long2，SHI Ning3，LUO Yong3

(1.HubeiQingJiangHydroelectricDevelopmentCo.,Ltd，Yichang443000，China；2.ChinaRailwayPortandChannelEngineeringGroupCo.,Ltd，Guangzhou510660，China；3.SchoolofGeoscienceandInfo-physics，CentralSouthUniversity，Changsha410083，China)

Abstract：For dam safety monitoring data,poor information and small sample problem are unavoidable.In this paper,the traditional GM(1,1) model is improved by optimizing the original data,the initial value and the background value.Taking the radial horizontal displacement samples of a dam,the two models are adopted to predict the displacement values respectively,and compared with the measured values.Compared with the traditional GM(1,1) model,the improved GM(1,1) model is effective and practical, of which the prediction accuracy is higher.

Keywords：dammonitoring；GM(1,1)model；improvedGM(1,1)model；forecasting

大坝在供水、能源、航运供给以及防洪等方面起着重大的作用，而大坝的贡献需建立在良性运行的基础之上。因此，为保障大坝的安全运行，必须针对大坝开展安全监测工作[1-3]。对大坝的外观变形监测可以获取大量的监测数据，通过对其采用统计分析方法处理，可以初步地掌握大坝的变形特征及规律，及时了解潜在的危机。在实际中，大坝施工期间及蓄水初期可能导致变形监测数据不足，在贫信息、小样本的情况下，很难对大坝的实际工作形态进行准确的预测[4,5]。灰色模型的提出为解决贫信息、小样本的问题提供了新的思路，传统灰色模型存在着一定的局限性[6]，如对于非指数增长趋势的数据，传统GM(1,1) 模型在拟合时，灰度较大，限制其精度[7]。为此，本文分别对原始数据、初始值以及背景值进行优化，改进传统GM(1,1) 模型，并以某大坝为例，验证改进模型的有效性与可行性。

1传统GM(1,1)模型的建模过程及其不足

1.1传统GM(1,1)模型

假定x(0)(k)为给定的非负数据序列，其中k=1,2,…,n，即

(1)

对序列x(0)(k)进行一次累加，生成一个新的累加序列

(2)

其中，累加后生成

(3)

通过累加，将无明显规律性的数据序列转化为递增变化的数列。一般来说，认为累加序列x(1)(k)是时间t的连续函数，将其用一阶微分方程表示

(4)

式中:a为灰发展系数，反映数据序列的增长速度，u为灰色作用量，它反映数据的内部变化。然后采用最小二乘法求解式(4)的微分方程

(5)

传统GM(1,1) 模型计算式:

(6)

可解得模型的时间响应函数

(7)

然后，将时间代入式(7)获得的数据进行一次累减，即可得到原始数据模型

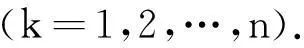
(8)

当k≤n时，得到的值是原始数据的拟合值；当k>n时，得到的数据为预测值。

1.2传统GM(1,1) 模型的不足之处

对上述建模过程进行分析，可以看出，传统GM(1,1) 模型存在以下不足：

1)传统GM(1,1) 模型的背景值一般是根据数值积分的梯形公式构造，当GM(1,1) 模型的灰发展系数a≥1时，该背景值构造方法的拟合与预测精度并不高。

2)灰发展系数a与灰色作用量u决定着传统GM(1,1) 模型的拟合与预测精度，而这两个系数受原始数据与背景值构造形式的影响；

2改进的GM(1，1)模型及精度评价

根据传统GM(1,1) 模型建模存在的不足，本文分别对原始数据、背景值以及初始值进行优化，用优化后的数据替代传统GM(1,1) 模型中相应的值，从而达到改进GM(1,1) 模型的目的，提高其预测精度。同时，为了比较GM(1,1) 模型改进前后预测结果的可靠性，选择了多种评价指标对预测结果进行评价。

2.1优化原始数据

原始数据是否满足指数增长的规律直接影响传统GM(1,1) 模型的预测结果，因此，当原始数据波动较大时，需对其进行处理以提高其光滑性，使其满足指数增长的规律，从而改善GM(1,1) 模型的预测精度。因此，本文采用滑动平均法对原始数据x(0)(k)进行预处理，生成新的序列

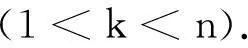
(9)

左右端点的计算式为

(10)

(11)

2.2优化背景值

由于灰色模型是指数预测模型，因此ea对模型的精度产生很大的影响，当a值较小时，预测曲线相对平稳，产生的误差也较小；若a值较大时，指数函数的结果会剧增，因此，将会产生较大的误差。根据指数函数自身的特性，采用下式改进背景值[8]。

(12)

(13)

其中，k=1,2,…,n-2.

2.3优化初始值

(14)

其中，ck=e-a(k-1)，

分别将改进方法后结果替代传统GM(1,1)模型中各计算值。

2.4精度检验

为验证模型预测的有效性，分别选用相对误差E、绝对误差Δ、均方差比值C以及小误差概率P四种指标来评价拟合及预测的效果。

1)相对误差E，反映预测残差占原始数据的比例，因此，E越小越好,

(15)

2)绝对误差Δ，表示拟合值、预测值与原始数据的接近程度，因此，Δ越小越好,

(16)

3)后验差比值C，越小越好，因为指标C反映原始数据离散程度大，而残差离散程度小，

(17)

其中，原始序列与预测序列的差值称为残差序列，S1是原始序列的标准差，S2是残差序列的标准差。

4)小误差概率P，指标P越大越好，由于残差与残差均值之差小于给定值，定义：

(18)

其中，e(0)(k)为残差序列。指标C与指标P的具体评定标准如表1所示[10]。

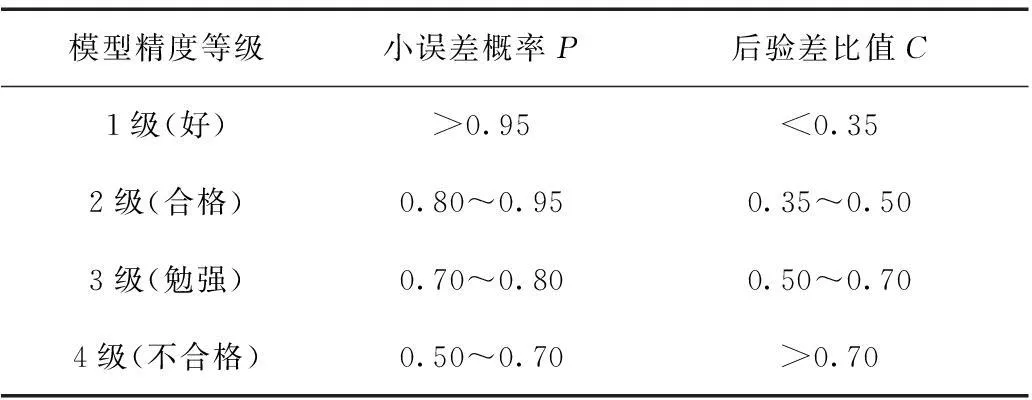
表1　模型精度评定标准

3实例分析

以2007-02-19～2011-06-19湖北省某大坝13期某测点径向水平位移数据为例，来验证改进后GM(1,1) 模型的可行性与有效性。其实测数据如表2所示。

选用前10期的实测数据分别用传统 GM(1,1) 模型与改进的 GM(1,1) 模型建立模型，剩下的3期数据作为预测比较数据。

1)对传统 GM(1,1) 模型进行预测求解，

(19)

然后，将预测时间代入式(17)，即可得到其预测值。

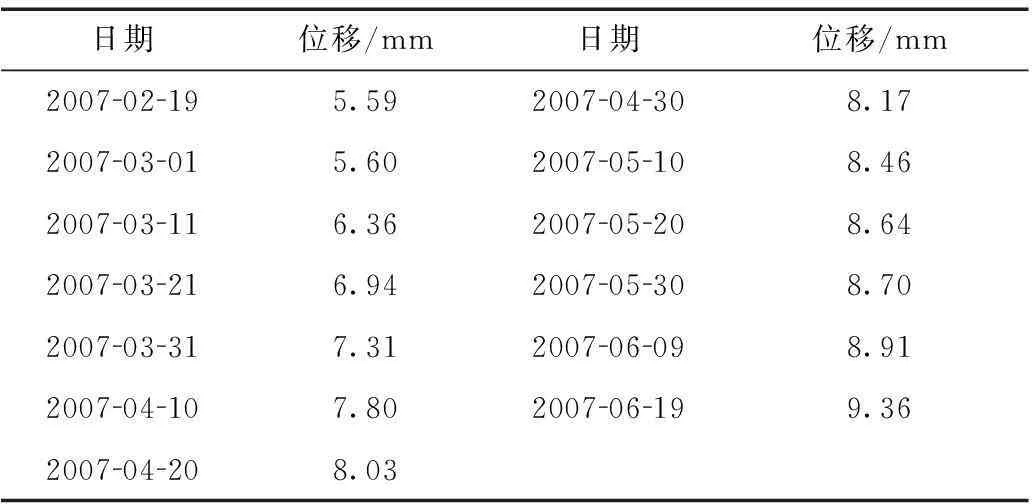
表2　某测点实测径向水平位移

2)对改进 GM(1,1) 模型进行建模预测。首先，确定原始数据序列进行滑动平均处理，得到优化后的数据序列X(0)(k)，然后，用式(13)、式(14)替代式(6)，对背景值序列进行优化，接着，利用优化后的背景值，按照式(14)对初始值进行优化，最后，将所有优化处理后的数据，按照传统 GM(1,1) 模型的步骤进行求解，得到的优化序列、优化背景值、优化初始值以及原始数据模型：

X(0)=[5.592,5.786,6.316,6.889,7.340,7.734,

8.006,8.206,8.430,8.607,8.737,8.969,9.244].

z(1)=[-8.441,-14.488,-21.101,-28.220,

-35.767,-43.643,-51.747,-60.069,-77.900].

(20)

两种模型的拟合精度结果如表3所示。

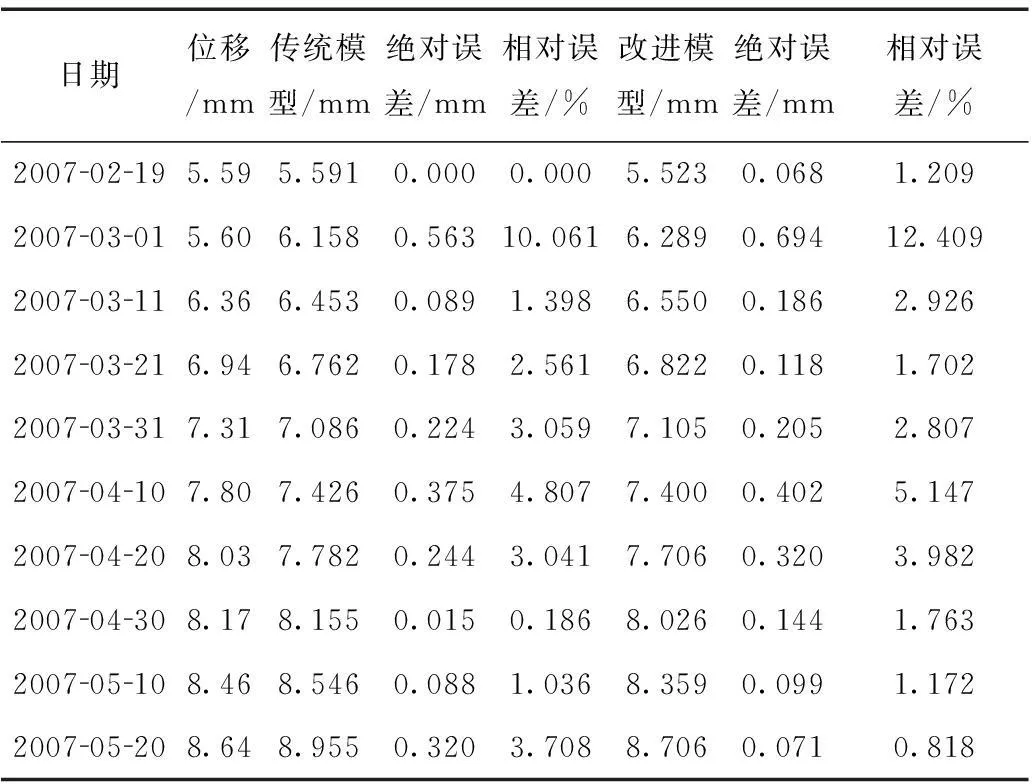
表3　两种模型拟合精度的比较结果

从表3中可以看出，传统 GM(1,1) 模型的相对误差与改进的 GM(1,1) 模型相差不大，这说明，改进的 GM(1,1) 模型相对于传统 GM(1,1) 模型并没有提高其拟合精度。两种模型预测精度的比较结果见表4。

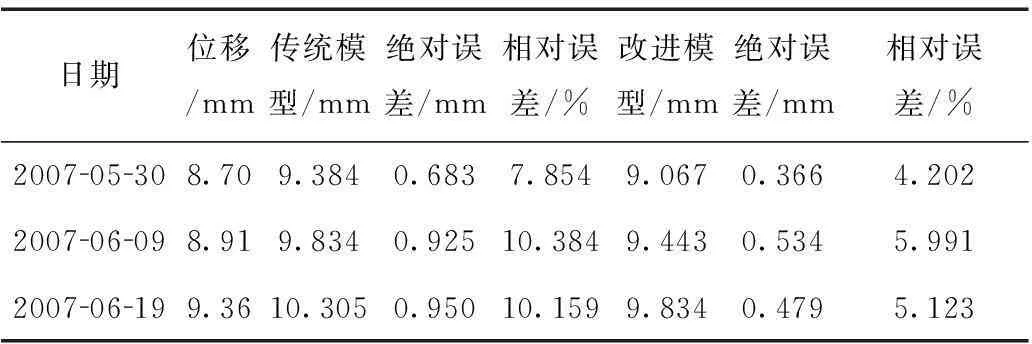
表4　两种模型预测精度的比较结果

尽管改进的 GM(1,1) 模型并没有提高拟合精度，但从表4的预测结果中可以看出，改进 GM(1,1) 模型的预测精度有明显改善，无论是相对误差还是绝对误差，都比传统 GM(1,1) 模型提高了1倍，这充分说明了改进的 GM(1,1) 模型的有效性。两种模型分别所在的精度等级见表5所示。

表5　两种模型分别所在的精度等级

然后，将两种模型的精度等级进行对比，从表4可以看出，尽管传统 GM(1,1) 模型的小误差概率P为1，位于1级，但其后验差比值C处于2级，而改进的 GM(1,1) 模型无论是后验差比值C还是小误差概率P都是1级，由此可以看出，改进的 GM(1,1) 模型要优于传统的 GM(1,1) 模型。

4结束语

本文通过对初始值、背景值以及原始数据进行优化处理，对传统 GM(1,1) 模型进行改进，通过对某大坝进行实证分析，改进的 GM(1,1) 模型预测精度有较为明显的改善，相对于传统的 GM(1,1) 模型，验证改进的 GM(1,1) 模型的有效性与优越性。对于受各种因素影响，导致大坝安全监测出现贫信息小样本的数据，采用改进的 GM(1,1) 模型相对于传统 GM(1,1) 模型具有一定的实用价值。

参考文献：

[1]郝少峰，方源敏，杨建文，等.基于熵权法的组合模型在滑坡变形预测中的应用[J].测绘工程，2014,23(7)：62-64.

[2]杨杰,吴中如.大坝变形监测的 BP 网络模型与预报研究[J].西安理工大学学报,2001,17(1)：25-29.

[3]苏怀智,温志萍,吴中如.基于 SVM 理论的大坝安全预警模型研究[J].应用基础与工程科学学报,2009,17(1)：40-48.

[4]高宁.贫信息小样本条件下时空动态变形预报方法研究[D].北京：中国矿业大学 ,2013.

[5]高宁，高彩云.危岩体变形位移预测的灰色双重优化模型[J].测绘科学，2014,39(4)：74-77.

[6]周吕，文鸿雁，韩亚坤.灰色预测与Kalman滤波在建筑物沉降变形分析中的应用[J].测绘科学，2014,39(4)：149-151.

[7]唐佑辉，黄腾，赵兵帅.GOM和时间序列组合模型在地表沉降预测中的应用[J].测绘工程，2014,23(2)：70-72.

[8]孙永荣,胡应东,陈武,等.基于GM (1,1) 改进模型的建筑物沉降预测[J].南京航空航天大学学报,2009,41(1)：107-110.

[9]唐万梅.几个预测方法及模型的研究[D].呼和浩特:内蒙古大学,2006.

[10]孙泽信，庞逸群，黄腾.改进的灰色模型在建筑物沉降预测中的应用[J].测绘工程，2010,19(3)：59-62.少峰，方源敏，杨建文，等.基于熵权法的组合模型在滑坡变形预测中的应用[J].测绘工程，2014,23(7)：62-64.

[2]杨杰,吴中如.大坝变形监测的 BP 网络模型与预报研究[J].西安理工大学学报,2001,17(1)：25-29.

[3]苏怀智,温志萍,吴中如.基于 SVM 理论的大坝安全预警模型研究[J].应用基础与工程科学学报,2009,17(1)：40-48.

[4]高宁.贫信息小样本条件下时空动态变形预报方法研究[D].北京：中国矿业大学 ,2013.

[5]高宁，高彩云.危岩体变形位移预测的灰色双重优化模型[J].测绘科学，2014,39(4)：74-77.

[6]周吕，文鸿雁，韩亚坤.灰色预测与Kalman滤波在建筑物沉降变形分析中的应用[J].测绘科学，2014,39(4)：149-151.

[7]唐佑辉，黄腾，赵兵帅.GOM和时间序列组合模型在地表沉降预测中的应用[J].测绘工程，2014,23(2)：70-72.

[8]孙永荣,胡应东,陈武,等.基于GM (1,1) 改进模型的建筑物沉降预测[J].南京航空航天大学学报,2009,41(1)：107-110.

[9]唐万梅.几个预测方法及模型的研究[D].呼和浩特:内蒙古大学,2006.

[10]孙泽信，庞逸群，黄腾.改进的灰色模型在建筑物沉降预测中的应用[J].测绘工程，2010,19(3)：59-62.

[责任编辑：李铭娜]